关于Wendt操作对链环交叉数的进一步结论

谭秋月， 孙平安， 林姝妤

(1. 武夷学院 数学与计算机学院， 福建 南平 354300；2. 武夷学院 实验室管理中心， 福建 南平 354300；3. 厦门大学 数学科学学院， 福建 厦门 361000)

关于Wendt操作对链环交叉数的进一步结论

谭秋月1， 孙平安2， 林姝妤3

(1. 武夷学院 数学与计算机学院， 福建 南平 354300；2. 武夷学院 实验室管理中心， 福建 南平 354300；3. 厦门大学 数学科学学院， 福建 厦门 361000)

研究纽结的一种解结操作——Wendt操作对链环交叉数的影响.计算纽结表中交叉指标不超过10的纽结，以及交叉指标不超过9的2分支链环的拟解结数，得到Wendt操作对这类链环的交叉数减二的结论.最后，通过投影图给予证明. 关键词： 纽结； 链环； Wendt操作； 解结数； 交叉指标

1 基本定义和引理

三维空间中，不与自己相交的连通分段线性闭曲线称为纽结，而由有限条既不自交也不互交的连通的分段线性闭曲线构成的空间图形称为链环.只要投影方向选取适当，总可使链环的平面投影图的自交点全部为二重点.为了反映产生二重点的弧线在三维空间的上下情况，用断开的弧线表示下线，用连续的弧线表示上线.这样二重点就变成了交叉点.以线的虚实表现交叉的情况，就得到链环的投影图.一个链环投影图称为可分离的，若它是由多个无公共交叉点链环投影图构成的，一个链环只有一个分离投影图,则称为不可分离或连通的.

设K为S3中的一个纽结，在K的所有投影图中，交叉点最少的那个投影图上的交叉点数就称为K的交叉指标，其符号为c(K).

设L为一个有向链环，VL(t)为L的Jones多项式[2]，定义spanv(L)为VL(t)的最高方次与最低方次之差，即spanv(L)=max degVL(t).

在文献[3]中，Kauffman定义了无向链环投影图的Kauffman尖括号多项式，假设D为链环无向投影图，设[D]=[D](A，B，d)为D的Kauffman方括号多项式，〈D〉=[D](A，A-1，-A2，-A-2)为Kauffman尖括号多项式，定义spank(D)为(D)的最高方次与最低方次之差，spank(D)=max deg〈D〉-min deg〈D〉.令L是一个有向链环，D为L的有向投影图，拧数w(D)定义为D的全体交叉点的正负号总和，Kauffman证明了VL(t)=(-A3)-w(D)〈D〉|A=t-1/4[2-3]，所以有spanv(L)=(1/4)spank(D).

引理1[2-4]令D为一个有向链环的无向投影图，则：1) 若L是连通交错链环，c(L)=spanv(L)=(1/4)·spank(D)；2) 若L是有n(L)个不可分分支的可分链环，c(L)=spanv(L)-n(L)+1=(1/4)·spank(D)-n(L)+1.

引理2[2，5]令D为连通约化交错链环的投影图，则有：1) max deg〈D〉=V+2W-2，V是D的交叉点数，W是B区域数，〈D〉中A的最高方次那一项对应的系数为(-1)W-1；2) max deg〈D〉=-V-2B+2，V是D的交叉点数，B是A区域数，〈D〉中A的最低方次那一项对应的系数为(-1)B-1.

由于链环投影图与符号平面图存在着一一对应，Kauffman[6]为符号图构建了Tutte多项式.设G为符号图，令Q[G]=Q[G](A，B，d)为对应G的Tutte多项式，简称为Q-多项式.

定义2[6]Q-多项式是按照如下两点循环规则来进行定义的.1) 若En是有n个顶点的无边图，则Q[En]=dn-1.2) (a) 如果e是桥，则Q[G]=(A+Bd)Q[G/e]，若s(e)=+；Q[G]=(B+Ad)Q[G/e]，若s(e)=-；(b) 如果e是环，则Q[G]=(B+Ad)Q[G-e]，若s(e)=+；Q[G]=(A+Bd)Q[G-e]，若s(e)=-；(c) 如果e既不是桥也不是环，则有Q[G]=BQ[G-e]+AQ[G/e]，若s(e)=+；而Q[G]=AQ[G-e]+BQ[G/e]，若s(e)=-.

引理3[6]设G是符号平面图，D(G)对应G的链环投影图，则Q[G]=[D(G)].

设G是符号平面图，G的分支对偶图G*是对图G的每个连通分支先各自求对偶图，由这些对偶图的不交并得到的图.注意到G中的边与G*中的边是一一对应的，对每个边e∈E(G)，在G*对应着符号与之相反的e*∈E(G*).

引理4 设G是符号平面图，G*为G对应的对偶图，则存在Q[G]=Q[G*].

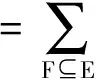
引理5 假设G=(V，E)是连通图，G+是基础图G的正图，则有Q[G+]=A-|E|+2|V|-2TG(-A-4，-A4).

2 解结数和Wendt操作说明

解结数的另一个等价定义，即任取纽结K的一个投影图，先任意选定一个交叉点做Wendt操作；接着，做一系列初等变化得到个新纽结的投影图；然后，在这个新的投影图上选定第二个交叉点做Wendt操作；再做一系列初等变化又得到个新纽结的投影图，依次进行下去，直至这个纽结变为平凡纽结.若存在纽结K的一个投影图，按照这个做法，只需n次改变交叉点就可使纽结变为平凡纽结，并且没有比n次更少的可能，那么,就称纽结K的解结数为n.显然,平凡纽结u(01)=0，其他纽结的解结数均大于等于1.

图1 三叶结的Wendt操作Fig.1 Triple junction Wendt operation

三叶结交叉指标为3，但是只需做一次Wendt操作就可以变成平凡纽结，所以u(31)=1，三叶结解结数为1，如图1所示.

定理1[9]任给一个纽结K的投影图，设其交叉点数为n，则总可以经过不超过⎣n/2次Wendt操作,把它变成平凡纽结的投影图.

推论1[9]设纽结K有一个交叉点数为n的投影图,则u(K)≤⎣n/2.

一般来说，很难找到纽结的解结数.比如，纽结83在纽结表[10]的投影图上看，解结数好像是2，但是纽结83还有很多其他的投影图.同样，为了证明一个复合结的解结数不可以为1，从问题提出到找到证明也经过了100多年的时间.纽结K的解结数u(K)的上界可以使用相对简单的技巧计算出来，但是却很难得到确切值.Scharlemann[1]在1985年证明了解结数为1的纽结都是素纽结.

下面的纽结解结数图表由Kirby[2]提供，其中，纽结929的解结数由Kirby证实，纽结10139，10152的解结数是由Kawamura[9]得出的，纽结949的解结数是由Stoimenow[11]用计算机计算出来的，纽结10154，10161则是Stoimenow[12]通过使用Slice-Bennequin不等式[13]找到的，纽结1011，1047，1051，1054，1061，1076，1077，10100的解结数目前为止依然未知.

已知具有n个交叉指数的素纽结总个数以指数级的速度增长.所以,文中只研究交叉指数少于10的纽结的解结数.因为u(K)=u(K*)，所以不考虑手性因素.

3 结论及其证明

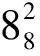
例1 链环820的Wendt操作，结果如表1所示.

表1 链环820每个交叉点经过一次Wendt操作的结果

投影图K的拟解结数的定义可参考文献[14-16].若经过Wendt操作得到的纽结为非交错纽结，则存在减少1的情况，如交错纽结933.

交叉点数少于10的交错纽结投影中，对其一个交叉点做Wendt操作，若得到的纽结仍然为交错纽结，则其交叉指标至少减少2；若不是，则不然.对交叉点数少于9的2个分支链环，此结论也成立，故这一规律在增加适当条件的基础上得到定理2.

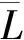
证明 令L为连通链环，其最约化交错投影图为D，因为L是连通的，则D一定是连通的.令G=G(D)为对应D的符号平图.不失一般性，假设G是正图，否则的话，可以根据引理1～4改为研究G*，因为是最约化的，所以G就是无环无桥.

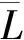
情况Ⅰ 无环.

的确是胡闹。西双说，假如我们真的又产生感情，真的对那段婚姻恋恋不舍，婚后真的可以夫妻恩爱白头偕老，复婚也未尝不可。但是可以肯定的是，我与她，不可能再有丝毫感情——我指的是夫妻间的那种感情。我去看她，我借给她钱，都不过只是怜悯——我不忍心让她死在那个出租屋里，就这样。

在这个情况下,G′是连通无环无桥的正图.因此,其对应的链环投影图也是连通最约化的交错投影图.令H为连通平图，v(H)，e(H)，f(H)分别定义为H的点数、边数和面数.通过引理2可得到如下4点结果.

1) max degQ[G]=max deg〈D〉=V+2W-2=e(G)+2f(G)-2，对应的系数为(-1)f(G)-1；

2) min degQ[G]=min deg〈D〉=-V-2B+2=-e(G)-2v(G)+2，对应的系数为(-1)v(G)-1；

3) max degQ[G′]=e(G′)+2f(G′)-2=e(G)+2f(G)-3，对应系数为(-1)f(G′)-1=(-1)f(G)-1；

4) min degQ[G′]=-e(G′)-2v(G′)+2=-e(G)-2v(G)+5，则其对应的系数为(-1)v(G′)-1=(-1)v(G)-1.

由此,还可以得到如下4点结果.

1) max degA2Q[G]=e(G)+2f(G)，对应的系数为(-1)f(G)-1；

2) max degA2Q[G]=-e(G)-2v(G)+4，对应的系数为(-1)v(G)-1；

3) max deg (A-1-A3)Q[G′]=e(G)+2f(G)，对应的系数为(-1)f(G)-1；

4) max deg (A-1-A3)Q[G′]=-e(G)-2v(G)+4，对应的系数为(-1)v(G)-1.

A2Q[G]与(A-1-A3)Q[G′]的最大方次可互相削去，由此得到

所以有

spanq(G)=max degQ[G]-min degQ[G]= 2e(G)+2f(G)+2v(G)-4，

2e(G)+2f(G)+2v(G)-12=spanq(G)-8.

图2 删除平行边e和f后的G图形变为G-e-f图形Fig.2 G into gigure G-e-f after delete parallel sides e and f

情况ⅡG′有环.令f为G′的任一个环.由于G是无环的，f一定是G的边e的平行边，再分两种情况讨论.

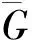
ⅱ) 如果G-e-f是连通的.首先知道f不是G′的桥.令g≠f为G′的边，因为G是无桥的，g属于G中一个圈C，若e∉E(C)，g属于G′中一个圈C中；若e∈E(C)，g属于G′中的一个圈G′=C-e+f，所以g不是桥.因此,G′为连通无环无桥的正图，同样由引理2可得到到如下4点结果.

1) max degQ[G]=max deg〈D〉=V+2W-2=e(G)+2f(G)-2，对应的系数为(-1)f(G)-1；

2) min degQ[G]=min deg〈D〉=-V-2B+2=-e(G)-2v(G)+2，对应的系数为(-1)v(G)-1；

3) max degQ[G′]=e(G′)+2f(G′)-2=e(G)+2f(G)-5，对应系数为(-1)f(G′)-1=(-1)f(G)-1；

4) min degQ[G′]=-e(G′)-2v(G′)+2=-e(G)-2v(G)+3，则其对应的系数为(-1)v(G′)-1=(-1)v(G)-1.

因此，可以得到如下4点结果.

1) max degA-2Q[G]=e(G)+2f(G)-4，对应的系数为(-1)f(G)-1；

2) max degA-2Q[G]=-e(G)-2v(G)，对应的系数为(-1)v(G)-1；

3) max deg (A-1-A-3)Q[G′]=e(G)+2f(G)-4，对应的系数为(-1)f(G)-1；

4) min deg (A-1-A-3)Q[G′]=-e(G)-2v(G)，对应的系数为(-1)v(G)-1.

A-2Q[G]与(A1-A-3)Q[G′]的最大方次可互相削去，由此可得

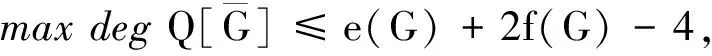
所以有

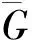
2e(G)+2f(G)+2v(G)-12=spanq(G)-8.

[1]SCHARLEMANNMG.Unknottingnumberoneknotsareprime[J].InventMath，1985,82(1):37-55.

[2]KAUFFMANLH.StatemodelsandtheJonespolynomial[J].Topology，1987,26(3):395-407.

[3]MURASUGIK.Jonespolynomialsandclassicalconjecturesinknottheory[J].Topology，1987，26(2):187-194.

[4]THISTILETHWAITEMB.AspanningtreeexpansionoftheJonespolynomial[J].Topology，1987，26(3):297-309.

[5]KAUFFMANLH.Newinvariantsinthetheoryofknots[J].AmerMathMonthly，1988(95):195-242.

[6]KAUFFMANLH.ATuttepolynomialforsignedgraphs[J].DiscreteApplMath，1989,25(1/2):105-127.

[7]BONDYJA，MURTYUSR.Graphtheoryanditsapplications[M].London:TheMacmillanPressLtd，1976:1-40.

[8]KIRBYR.Problemsinlow-dimensionaltopology[C]∥GeorgiaTopologyConference.Providence:[s.n.],1996:35-473.

[9]KAWAMURAT.Theunknottingnumberof10139and10152are4[J].OsakaJMath，1998,35(3):539-546.

[10] ADAMS C C.The knot book[M].New York:American Mathematical Society Providence Ri,1994:307.

[11] STOIMENOW A.Polynomial values， the linking form， and unknotting numbers[J].Math Res Lett,2004,11(5/6)：755-769.

[12] STOIMENOW A.Positive knots, closed braids and the Jones polynomial[J].Annali Della Scuola Normale Superiore Di Pisa Classe Dienze,1998,2(2):237-285.

[13] JONES V F R.A polynomial invariant for knots via von Neumann algebras[J].Bull Amer Math Soc,1985,12(1):103-111.

[14] 谭秋月,孙平安,林姝妤.Wendt操作对纽结和链环影响的若干规律[J].石家庄学院学报,2015,17(6):61-66.

[15] 李景文，吕楠，陆妍玲，等.对象化BR-TIN模型三维地理信息组织方法[J].华侨大学学报(自然科学版)，2015，36(4):383-387.

[16] 汪秋分,宋海洲.图的拉普拉斯谱半径对应的特征向量性质及其应用[J].华侨大学学报(自然科学版),2014,35(1):107-111.

(责任编辑： 黄晓楠 英文审校： 黄心中)

Further Conclusion of Crossing Number of Links Based on Wendt Operation

TAN Qiuyue1， SUN Ping′an2， LIN Shuyu3

(1. School of Mathematics Science and Computer， Wuyi University， Nanping 354300， China；2. Laboratory Management Center， Wuyi University， Nanping 354300， China；3. School of Mathematical Sciences， Xiamen University， Xiamen 361000， China)

The effect of a single splitting operation, Wendt operation on the crossing number of the link diagrams is researched. We calculate the Quasi-splitting number of these two numbers for knots, which are with crossing number no more than 10, and with crossing number no more than 9 and 2-comonent links in the Knot table. One conclusion is that the Wendt operation can make the crossing number of these link diagrams minus two. In the last, we give a strict graph-theoretical proof by the projection drawings. Keywords： knot； link； Wendt operation； unknotting number； crossing number

10.11830/ISSN.1000-5013.201702027

2017-02-14

谭秋月(1980-)，女，副教授，主要从事图论、离散数学的研究.E-mail:tqyspa@163.com.

福建省教育厅科技项目(JA1551)； 福建省大学生创新创业训练计划项目(201510397029)； 武夷学院科研基金资助项目(XL201409)

O 157.5

A

1000-5013(2017)02-0276-05