食饵有病的生态-流行病模型的稳定性分析
2017-04-07傅金波陈兰荪
傅金波, 陈兰荪,2
(1. 福建师范大学 闽南科技学院, 福建 泉州 362332;2. 中国科学院 数学与系统科学研究院, 北京 100080)

食饵有病的生态-流行病模型的稳定性分析
傅金波1, 陈兰荪1,2
(1. 福建师范大学 闽南科技学院, 福建 泉州 362332;2. 中国科学院 数学与系统科学研究院, 北京 100080)
研究一类具有双线性发生率和功能反应且食饵染病的生态-流行病模型的动力学行为.通过构造适当的Lyapunov函数,运用LaSalle不变集原理,获得保证系统的无捕食者无病平衡点、疾病主导平衡点、捕食者主导平衡点和正平衡点全局渐近稳定的阀值条件.通过疾病流行的阀值和捕食机制形成的阀值,以及疾病与捕食两者竞争占优的阀值,共同刻画生态-流行病系统的演变规律性. 关键词: 生态-流行病模型; Lyapunov函数; LaSalle不变集原理; 功能性反应; 平衡点; 全局稳定性
1 预备知识
近年来,许多学者利用种群动力学原理[1]和Kermack[2]的流行病学建模机理,分析了大量的食饵-捕食者系统[3-8]和多种形式的传染病模型[9-14].然而,在已有的生物动力学模型建模中考虑疾病影响却不多见.疾病对种群的影响是一个不可忽视的重要问题.将种群动力学与传染病学结合起来所建立的生态-流行病模型,对于探讨疾病流行对生态环境的影响,乃至改善生态环境以控制疾病的流行,无疑是一个新的研究方向,更富有实际应用价值[15].据此,考虑疾病只在食饵之间传播,且食饵种群分为易感者和染病者两类,建立食饵有病的生态-流行病模型为
(1)
式(1)中:S,I分别为t时刻食饵种群中易感者和染病者两类的数量;Y为t时刻捕食者种群的数量;A为易感者种群的增长率;β为接触率;p为捕食率;di(i=1,2)为自然死亡率;g为捕食者种群的增长率;所有参数均为正的常数,且g 基于生物学意义,模型(1)的初值条件为S(0)>0,I(0)>0,Y(0)>0.定义3个阀值依次为 且 文中主要研究模型(1)的无捕食者无病平衡点、疾病主导平衡点、捕食者主导平衡点和正平衡点的全局渐近稳定性,从理论上阐明捕食与疾病流行的演变规律性. 引理1 模型(1)满足初值条件的任意解(S,I,Y)皆为正解. 证明 模型(1)等价于 (2) 由此可见,在初值条件下,模型(1)的任意解(S,I,Y)皆为正解.证毕. 引理2 模型(1)满足初值条件的任意正解(S,I,Y)均为最终有界的. 证明 令L=S+I+Y,由模型(1)得L′≤A-d1S-d1I-d2Y.取μ=min{d1,d2},故有 由微分方程比较定理可知,存在t0>0,M≥M0,当t≥t0时,恒有L≤M.进而,集合Ω={(S,I,Y)∈R3∶0 模型(1)的非负平衡点满足 (3) 根据方程组(3),易获得如下结论. 引理3 模型(1)总存在着无捕食者无病平衡点P0=(S0,0,0).当R0>1时,存在疾病主导平衡点P1=(S1,I2,0);当R1>1时,存在捕食者主导平衡点P2=(S2,0,Y2);当R1>1,且R2>1时,还存在正平衡点P3=(S3,I3,Y3). 定理1 当R0≤1,R1≤1时,模型(1)的无捕食无病平衡点P0在域Ω上是全局渐近稳定. 证明 将模型(1)改为如下等价系统,即 (4) 设(S,I,Y)是系统(4)的任意正解,利用函数F(ξ)=ξ-1-lnξ在(0,+∞)存在唯一最小值点ξ=1且F(ξ)≥F(1)=0的性质,构造Lyapunov泛函为 易见正定函数V0(t)在无捕食无病平衡点P0处取得唯一最小值为零.当R0≤1,R1≤1时,直接计算V0(t)沿着系统(4)轨线的全导数,可得 根据LaSalle不变性原理[16]可知:模型(1)的无捕食无病平衡点P0在域Ω上是全局渐近稳定的.证毕. 定理2 当R0>1≥R1时,模型(1)的疾病主导平衡点P1在域Ω上是全局渐近稳定. 证明 将模型(1)改为如下等价系统,有 (5) 设(S,I,Y)是系统(5)的任意正解,利用函数F(ξ)=ξ-1-lnξ在(0,+∞)上的非负性质,构造Lyapunov泛函为 由此可见,正定函数V1(t)在疾病主导平衡点P1处取得唯一最小值为零. 当R0>1≥R1时,注意到βS1=d1,直接计算V1(t)沿着系统(5)轨线的全导数,可得 当R0>1,R1>1时,特征方程存在一个正特征值,故P1是不稳定的;当R0>1≥R1时,特征方程的非零特征值均具有负实部,而且零特征值为特征单根,故P1是局部渐近稳定. 由LaSalle不变性原理[16]可以得到,模型(1)的疾病主导平衡点P1在域Ω上是全局渐近稳定的.证毕. 定理3 当R1>1≥R2时,模型(1)的捕食者主导平衡点P2在域Ω上是全局渐近稳定. 证明 将模型(1)改为如下等价系统,有 (6) 设(S,I,Y)是系统(6)的任意正解,利用函数F(ξ)=ξ-1-lnξ在(0,+∞)上的非负性质,构造Lyapunov泛函为 由此可知,正定函数V2(t)在捕食者主导平衡点P2处取得唯一最小值为零. 当R1>1≥R2时,注意到gS2=d2,沿着系统(6)轨线计算V2(t)的全导数,可得 当R1>1,R2>1时,特征方程存在一个正特征值,故P2是不稳定的;当R1>1≥R2时,特征方程的非零特征值均具有负实部,而且零特征值作为特征单根,故P2是局部渐近稳定. 根据LaSalle不变性原理[16]可知:模型(1)的捕食者主导平衡点P2在域Ω上是全局渐近稳定的.证毕. 定理4 当R1>1,R2>1时,模型(1)的正平衡点P3在域Ω内是全局渐近稳定. 证明 将模型(1)改为如下等价系统,有 (7) 设(S,I,Y)是系统(7)的任意正解,利用函数F(ξ)=ξ-1-lnξ在(0,+∞)上的非负性质,构造Lyapunov泛函为 易于验证正定函数V3(t)在正平衡点P3处取得唯一最小值为零. 同时,模型(1)在P3处Jacobian矩阵的特征方程为 其中:a1=d1+βI3+pY3;a2=β2S3I3+pgS3Y3+pgI3Y3;a3=pgI3Y3(d1+βI3+pY3). 又因为Δ1=a1,Δ2=a1a2-a3=(d1+βI3+pY3)(β2S3I3+pgS3Y3),Δ3=a3Δ2皆为正数,故由Routh-Hurwitz判据[16]可知:当R1>1,R2>1时,P3总是局部渐近稳定. 由LaSalle不变性原理[16]可知:模型(1)的正平衡点P3在域Ω内是全局渐近稳定的.证毕. 由定理1可知:当食饵种群的易感者染病数量不多于1个,且捕食者种群的捕食数量也不多于1个时,该生态-流行病系统中的疾病尚未流行,且捕食机制也尚未形成,疾病和捕食者种群将在该系统中很快被消除,食饵种群的易感者数量将全局渐近稳定在一个正常数上. 由定理2可知:当食饵种群的易感者染病数量大于1个,且捕食者种群的捕食数量不多于1个时,该生态-流行病系统中疾病流行,且捕食机制尚未形成,捕食者种群在系统中趋于灭绝,食饵种群的易感者和染病者数量将全局渐近稳定在一组正常数上. 由定理3可知:当捕食者种群的捕食数量大于1个,且疾病低于捕食对食饵种群的侵害,该生态-流行病系统中疾病尚未流行,且捕食机制已形成,疾病在系统中很快消除,食饵种群的易感者和捕食者数量将全局渐近稳定在一组正常数上. 由定理4可知:当捕食者种群的捕食数量大于1个,且疾病还高于捕食对食饵种群的侵害,该生态-流行病系统中捕食机制已形成且疾病流行,食饵种群的易感者、染病者和捕食者种群共存并将全局渐近稳定在一组正常数上. 综上讨论,R0是疾病是否流行的阀值,R1是捕食机制是否形成的阀值,R2是疾病与捕食两者占优比较的阀值,三者共同刻画了生态-流行病系统(1)的演变规律性. [1] 陈兰荪,陈键.非线性生物动力系统[M].北京:科学出版社,1993:102-130. [2]KERMACKWO,MCKENDRICKAG.Contributionstothemathematicaltheoryofepidemics[J].BulletinofMathematicalBiology,1991,53(1):33-55. [3] 李林.一个环境数学模型的一致持久性与稳定性[J].应用数学学报,2003,26(1):149-157. [4] 程荣福,李辉.一个具功能性反应的微分生态系统的定性分析[J].东北师大学报(自然科学版),2005,37(1):11-15. [5]CHENFengde,SHIJinlin.Periodicityinalogistictypesystemwithseveraldelays[J].ComputersandMathematicswithApplications,2004,48(1/2):35-44. [6] 张正球,王志成.基于比率的三种群捕食者-食饵扩散系统的周期解[J].数学学报,2004,47(3):531-540. [7] 范猛,王克.一类具有HollingⅡ型功能性反应的捕食者-食饵系统全局周期解的存在性[J].数学物理学报,2001,21(4):83-91. [8] 徐瑞,陈兰荪.具有时滞和基于比率的三种群捕食系统的持久性与全局渐近稳定性[J].系统科学与数学,2001,21(2):204-212. [9]YOSHIDAN,HARAT.GlobalstabilityofadelayedSIRepidemicmodelwithdensitydependentbirthanddeathrates[J].ComputationalandAppliedMathematics,2007,201(2):339-347. [10] 侯强,靳祯.一个基于修正的Leslie-Gower 生态传染病模型的研究[J].中北大学学报(自然科学版),2012,33(2):98-101. [11] 张少辉,靳祯.具有非线性发生率的传染病模型性态分析[J].中北大学学报(自然科学版),2012,33(4):353-357. [12] 刘玉英,肖燕妮.一类受媒体影响的传染病模型的研究[J].应用数学和力学,2013,34(4):399-407. [13] 傅金波,陈兰荪,程荣福.具有潜伏期和免疫应答的时滞病毒感染模型的全局稳定性[J].高校应用数学学报(A辑),2015,30(4):379-388. [14] 傅金波,陈兰荪,程荣福.具有Logistic增长和治疗的SIRS传染病模型的后向分支[J].吉林大学学报(理学版),2015,53(6):1166-1170. [15] LI Jianquan,ZHANG Juan,MA Zhien.Global analysis of some epidemic models with general contact rate and constant immigration[J].Applied Math Mech,2004,25(4):396-404. [16] 马知恩,周义仓.传染病动力学的数学建模与研究[M].北京:科学出版社,2004:178-192. (责任编辑: 钱筠 英文审校: 黄心中) Stability Analysis of Eco-Epidemiologic Model With Disease in Prey FU Jinbo1, CHEN Lansun1,2 (1. Minnan Science and Technology Institute, Fujian Normal University, Quanzhou 362332, China;2. Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing 100080, China) In this paper, the dynamical behaviors of the eco-epidemiologic model with double linearity incidence rate, functional response and disease in the prey are studied. By constructing suitable Lyapunov function and using LaSalle invariance principle, the global asymptotic stable threshold conditions of non-predator disease-free equilibrium, disease dominant equilibrium, predator dominant equilibrium and positive equilibrium in the system are obtained. The threshold of disease popularity, the threshold of formation of predation mechanism and the threshold of dominance of disease or predator in their competition depict the evolvement law of the eco-epidemiologic system. Keywords: eco-epidemiologic model; Lyapunov function; LaSalle invariance principle; functional response; equilibrium point; global stability 10.11830/ISSN.1000-5013.201702025 2016-09-09 傅金波(1978-),男,副教授,主要从事生物数学的研究.E-mail:fujinbomnkjxy@sina.com. 国家自然科学基金资助项目(11371306); 福建省教育厅自然科学基金资助项目(JA13370); 福建师范大学闽南科技学院青年骨干教师重点项目(MKQ201006) O 175.13 A 1000-5013(2017)02-0266-052 相关引理及其证明
3 主要结果与证明


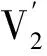

4 结论
