基于固有频率的呼吸式裂纹梁损伤识别方法

刘文光 郭隆清 贺红林 颜 龙

南昌航空大学航空制造工程学院，南昌，330063

基于固有频率的呼吸式裂纹梁损伤识别方法

刘文光 郭隆清 贺红林 颜 龙

南昌航空大学航空制造工程学院，南昌，330063

将呼吸裂纹梁简化为由扭转弹簧连接的两段弹性梁，在假定振动响应随振幅变化的基础上推导出呼吸裂纹梁的固有频率方程；考虑振动过程中呼吸裂纹的开合情况，假定裂纹梁的刚度是振幅的非线性函数，建立了呼吸裂纹梁的多项式刚度模型；结合等高线裂纹识别理论和方法，提出了一种基于固有频率的呼吸裂纹梁损伤识别方法，算例验证了方法的可行性与有效性。研究表明，该方法的识别精度取决于实验固有频率的精度。

呼吸裂纹；固有频率；损伤识别；等高线法

0 引言

梁是机械结构或系统中常见的构件之一，引致梁失效的主要形式之一是疲劳裂纹。服役于振动环境之下的梁，诸如直升机的旋翼叶片、飞机的机翼以及发动机的叶片等，均不可避免地会因裂纹的疲劳扩展及其呼吸效应使得梁的振动特性随振幅变化而改变，在动力学行为上表现为振动非线性。非线性给呼吸式裂纹梁的振动预测带来非常大的困扰，不少学者在研究裂纹梁动力问题时，通常都假定裂纹在振动过程中始终处于张开状态[1-2]，以避开裂纹呼吸效应给振动分析带来的麻烦。这种建模的思路与方法，从物理现象来看，显然与客观事实不符。

为了推动基于振动理论的结构健康监测技术的发展，很多学者围绕含裂纹构件的损伤识别振动方法进行了深入研究。CORNWEL等[2]利用板损伤前和损伤后的振型，基于应变能量法对板结构的损伤进行识别和定位，该方法实质就是STUBBS等[3]提出的一维应变能法的延伸。刘文光等[4]基于结构单元损伤前后模态应变能的变化率构建损伤指标，提出了弹性梁损伤识别模态应变能法。YANG等[5]在假定裂纹附近应变能会发生改变的基础上，研究了张开式裂纹对弹性梁振动特性的影响。SWAMIDAS等[6]结合能量法和断裂力学建立了张开型裂纹模型，求解了张开裂纹和无损伤梁的固有频率。吴国荣[7]利用无质量扭转弹簧等效裂纹截面,建立了含裂纹梁的等效动力学模型，推导出了含张开式裂纹梁的传递矩阵和固有频率方程。考虑呼吸裂纹闭合效应对裂纹梁振动行为的影响，KISA等[8]建立了考虑振动后半周期裂纹闭合产生的接触刚度模型，但是此模型仅考虑了裂纹全开和全闭状态，忽略了裂纹开合中的部分开合状态。于是，CHENG等[9]通过周期函数描述呼吸裂纹梁的刚度模型，建立了含时变刚度的单自由度模型；BOVSUOVSKY等[10]应用双线性刚度模型描述裂纹的呼吸行为；ABRAHAM等[11]忽略系统阻尼的影响，通过傅里叶多项式级数模拟了呼吸裂纹刚度的变化。

尽管研究者在含裂纹的结构动力学分析方法上做了大量研究，但很少文献考虑结构刚度因裂纹呼吸行为随振幅变化而发生变化，更少研究考虑裂纹接触刚度和阻尼对损伤识别的影响。本文在考虑裂纹梁刚度随振幅变化的基础上，研究一种呼吸式裂纹梁的固有频率计算方法，结合等高线裂纹识别方法与理论，提出一种基于固有频率的呼吸式裂纹梁损伤识别技术。

1 呼吸式裂纹梁的固有频率方程

以图1a所示的含裂纹悬臂梁为对象，假定梁的长度为L，宽度为w，高度为h，裂纹深度为a，裂纹位置与固定端的距离为L0。考虑裂纹引起的柔度，利用扭转弹簧代表裂纹，含裂纹梁被描述为通过扭转弹簧连接起来的两根无损伤梁，其等效模型如图1b所示。工作时，一旦梁激发自由振动，裂纹会随梁振幅的改变交替出现张开与闭合的情况，导致梁的刚度随振幅变化发生相应变化，使梁的动力学行为发生复杂反应。

(a)几何模型 (b)等效模型图1 含疲劳裂纹的悬臂梁模型Fig.1 Model of canlitiever beam with fatigue crack

忽略阻尼和裂纹对梁振型的作用，把裂纹位置的局部刚度描述为非线性无质量扭转弹簧，则其刚度变化取决于裂纹的开合程度(即与振幅有关)。此疲劳裂纹梁的运动方程可以描述为

(1)

式中，E为材料的弹性模量；I为截面关于中性轴的惯性矩；ρ为材料密度；S为截面面积；w1和w2分别为对应裂纹左右边弹性梁的横向位移函数；x为纵向坐标；t为时间。

因为裂纹位置的局部刚度取决振幅函数，所以梁的固有频率及其振型也随振幅的变化发生改变。梁的振动响应可表示为

(2)

式中，A(t)为梁轴线运动时指定位置的位移；φ1(x,A(t))和φ2(x,A(t))分别为左右边弹性梁与振幅有关的特征函数。

把振动响应函数(式(2))代入运动方程(式(1))，可得到

(3)

式中，ci(i=1,2,…,8)为与边界条件有关的待定系数；ω为圆频率；λ和ω与时间有关。

呼吸裂纹梁两端的边界条件为

(4)

梁裂纹x=L0位置处，相应的连续性条件为

(5)

梁裂纹x=L0位置处，还有一个斜率条件为

EIφ1,xx(L0,A(t))=
kA[φ2,x(L0,A(t))-φ1,x(L0,A(t))]

(6)

式中，kA为随振幅变化的呼吸裂纹梁刚度。

上述4个边界条件(式(4))、3个连续性条件(式(5))、1个斜率条件(式(6))，构成了行列式特征值问题，为了得到ci的量纲一解，行列式的特征值必须为零，即

|Δ(ω,L0,A(t))|=0

(7)

由此可推出含呼吸式裂纹梁的固有频率方程：

(8)

其中

F(β)=[cos(βλL)sinh(βλL)-sin(βλL)cosh(βλL)]-
[cos(βλL)sinh(βλL)+sin(βλL)cos(βλL)+
sinh(βλL)cosh(βλL)+sin(βλL)cosh(βλL)]·
sin(λL)sinh(λL)+[cos(βλL)sinh(βλL)-
sin(βλL)cosh(βλL)]cos(λL)cosh(λL)+
[cos(βλL)cosh(βλL)+cosh2(βλL)+
sin(βλL)sinh(βλL)]sin(λL)cosh(λL)+
[sin(βλL)sinh(βλL)-cos(βλL)cosh(βλL)-
cos2(βλL)]cos(λL)sinh(λL)

式中，β为裂纹相对位置，β=L0/L。

由式(8)可知，呼吸式裂纹梁的固有频率变化取决于刚度kA的变化，而kA的变化规律与梁的振幅衰减程度、裂纹深度有关。因此，在建立呼吸裂纹梁刚度模型的基础上，通过固有频率方程可以分析裂纹处于不同位置、不同深度以及不同振幅条件下的悬臂梁固有频率。

2 随振幅变化的含裂纹梁刚度模型

为便于建立含裂纹梁的刚度模型，不考虑系统阻尼的影响。如图1a所示，假定梁的轴线过平衡位置O向上运动，转角θ+增大，在此半个运动周期内裂纹将完全闭合，此时，梁的刚度与无裂纹梁的刚度完全一样；反之，如果梁的轴线过平衡位置O向下运动，则转角θ-增大，随着θ-值的增大，裂纹从完全闭合状态逐渐过渡到完全张开状态。实际上，受系统阻尼的影响，含裂纹梁的自由振动会随时间逐渐衰减。换言之，梁自由振动过程中，裂纹的运动会受阻尼的抑制，即梁的刚度变化范围逐渐缩小。

假设采用二次多项式近似描述裂纹梁刚度与振幅之间的关系，其表达式为

kA=a0+a1A+a2A2

(9)

式中，A为轴线自由端的振幅；a0、a1、a2为待定系数，取决于设定的边界条件。

假设裂纹完全张开时，裂纹梁的刚度等于开裂纹梁的刚度，裂纹闭合时，裂纹梁的刚度等于无损伤梁的刚度。所以，裂纹梁的刚度与振幅之间应满足以下关系：

式中，AO为裂纹全开时轴线自由端的振幅；AC为裂纹全闭时轴线自由端的振幅；kC为裂纹全闭时梁的刚度；kO为裂纹全开时梁的刚度。

利用插值原理和以上条件，可得到含裂纹梁的刚度模型：

(10)

裂纹全开状态下，含裂纹梁的局部刚度计算表达式为[12]

(11)

J(α)=0.6272α2-0.4533α3+4.5948α4-9.973α5+20.2984α6-33.0351α7+47.1063α8-40.7556α9+19.6α10

式中，μ为材料泊松比；J(α)为量纲一局部柔度；α为相对裂纹深度，α=a/h。

量纲一柔度计算公式对于α∈[0，0.5]情况比较符合。

3 裂纹识别方法与理论

如果定义由裂纹位置和深度确定固有频率称为正问题，那么由固有频率识别裂纹位置和深度则称为逆问题。基于固有频率方程，对应于不同的裂纹位置和裂纹深度，可以得到各阶次固有频率，同样，如果已知梁的固有频率，也可以由已知的固有频率与裂纹位置和深度的关系式，求解出裂纹的位置和深度。含呼吸式裂纹梁的固有频率方程是考虑了裂纹位置、裂纹深度和振动幅值的三元函数，为方便损伤识别，若取呼吸裂纹开合过程中梁固有频率的平均值作为对应裂纹位置、裂纹深度的固有频率值，固有频率就简化为裂纹位置、深度的二元函数。从求解线性方程组的角度来看，通过固有频率识别裂纹位置、裂纹深度，只需知道两阶固有频率就可以求得唯一解。为了避免振动测量中的节点效应并考虑工程测试中高阶模态频率误差相对较大的实情，实测频率一般仅取前三阶固有频率值进行识别。

结合裂纹梁的固有频率方程和刚度模型，基于等高线法可识别出裂纹位置和深度。首先，拟合出以裂纹位置和深度为自变量的固有频率响应面；然后，将实测固有频率代入到频率响应面上，得到若干条频率等高线并投影到同一平面，等高线理论上必然存在一个交点，这个交点横纵坐标即对应裂纹位置和裂纹深度。图2为对应某一裂纹参数的固有频率等高线图，三阶固有频率等高线由三段曲线组成，二阶模态频率等高线由两段曲线组成，一阶模态频率等高线只有一段曲线[13]。

1.第一阶固有频率等高线 2.第二阶固有频率等高线 3.第三阶固有频率等高线图2 等高线图Fig.2 Diagram of contour line

工程实际中，通过实测频率所得的三条等高线可能无法准确地交于一点，此时可以选取三条曲线互相交点所形成的小三角形的形心来确定裂纹位置和深度。

4 算例分析与验证

采用两个算例验证本文所提方法。算例1为利用裂纹梁解析固有频率进行验证，算例2为利用文献测得的实验固有频率进行验证。每个算例均采用6种不同裂纹工况呼吸裂纹梁的前三阶固有频率进行分析。

4.1 算例1

假设含呼吸裂纹悬臂梁的几何尺寸：梁长度L=300 mm，横截面高度h=8 mm，宽度w=20 mm。材料的弹性模量E=68.9 GPa，密度ρ=2750 kg/m3。对于已知裂纹相对位置和相对深度，基于固有频率方程可以构造考虑裂纹位置、深度的固有频率响应曲面。为了验证该方法的合理性，设计出6种不同的裂纹工况，并利用固有频率方程解出梁的前三阶固有频率，见表1。

表1 不同裂纹条件下的前三阶固有频率

把表1中各种工况条件下的前三阶固有频率代入裂纹梁固有频率响应面，可得到对应的固有频率等高线，将等高线投影到水平面，得到对应工况裂纹相对位置和深度的关系曲线，如图3所示。

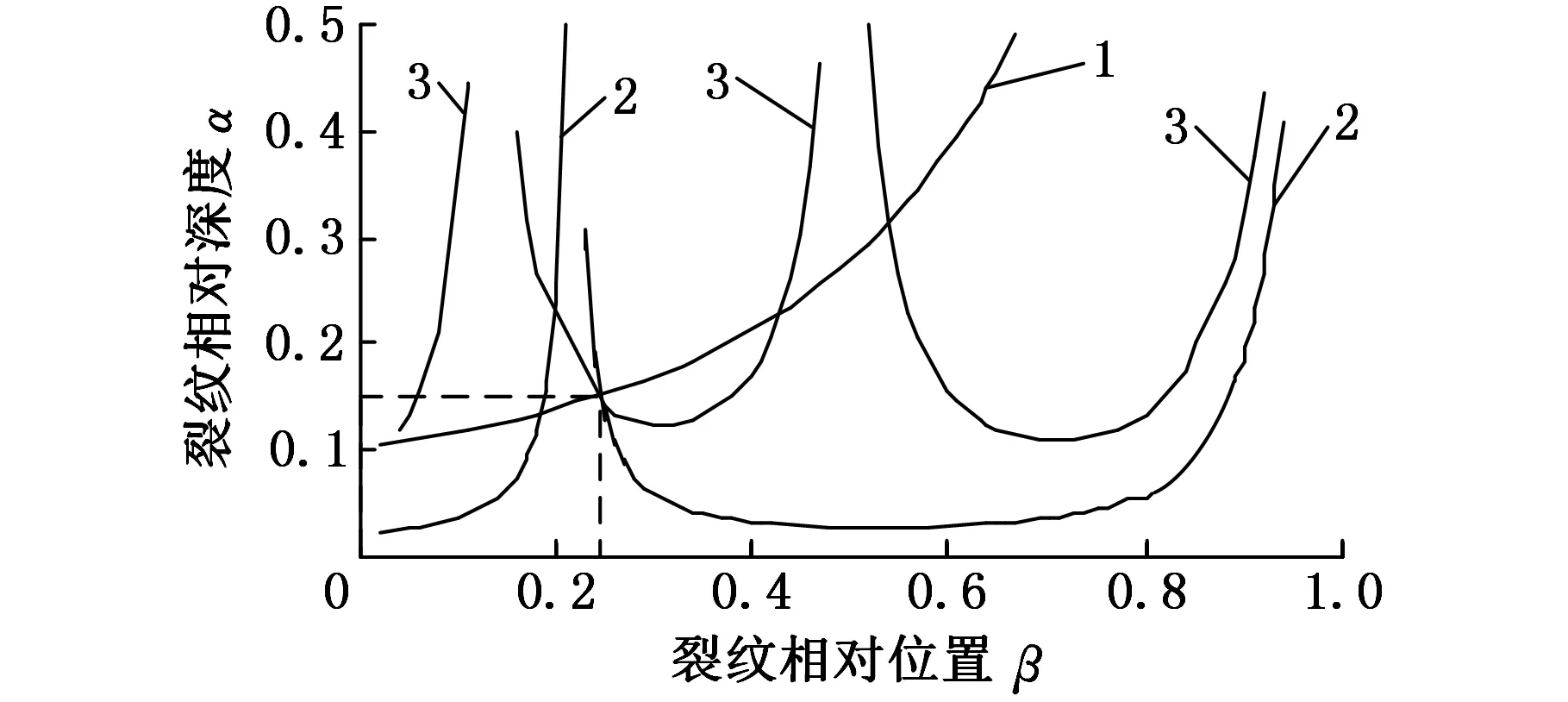
(a)工况a

(b)工况b

(c)工况c

(d)工况d

(e)工况e

(f)工况f1.第一阶固有频率等高线投影 2.第二阶固有频率等高线投影 3.第三阶固有频率等高线投影图3 裂纹参数识别1Fig.3 Case 1 of crack parameters identification

从图3中可以看出，三条等高线非常精准地相交于一点，交点的横纵坐标即为对应裂纹的相对位置和相对深度，因而可以非常方便地得到裂纹参数。比较识别出的裂纹参数与试件的实际解析解裂纹参数，计算两者之间的误差，结果如表2所示。

表2 等高线法悬臂梁裂纹参数识别结果1

从表2中可以看出，裂纹相对深度的识别效果的相对误差不会超过0.32%，裂纹相对位置的识别效果的相对误差不会超过0.93%。对于有效长度为300 mm、截面高度为20 mm的悬臂裂纹梁，裂纹深度识别误差不超过0.064 mm，裂纹位置的识别误差不超过2.79 mm，精度相当高，这证明了用等高线裂纹识别方法对裂纹参数进行检测的可行性。

4.2 算例2

实测固有频率通过振动测试技术可以得到，它不依赖于所选择的结构动力学模型，可以与动力学分析同步进行。下面的裂纹识别将以实测固有频率作为输入进行裂纹参数的识别。

取文献[14]中含裂纹梁的材料属性和几何尺寸进行损伤识别验证。材料弹性模量E=206 GPa，密度ρ=7750 kg/m3，梁的有效长度L=300 mm，梁的横截面高度h=20 mm，宽度w=20 mm。基于已知的几何尺寸、材料参数和固有频率方程可构造梁的固有频率响应面。采用文献[14]给出的实验测得的各种裂纹工况的前三阶固有频率值(表3)可进一步验证本文方法的合理性。

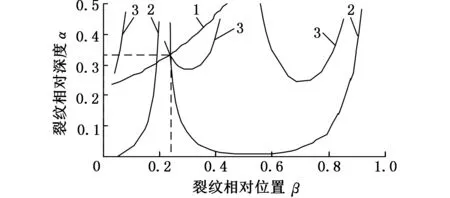
将表3中各裂纹工况的前三阶实测固有频率代入固有频率响应面，得到相应的频率等高线，并将等高线投影到水平面，得到裂纹梁的相对裂纹深度和裂纹位置的关系曲线，如图4所示。

从图4中可以看出，对于实测固有频率，三条等高线并不交于一点，故无法得到三条等高线的交点，只能确定两两之间的交点。此时，可以选取三条曲线交点所形成的小三角形的形心来确定裂纹相对位置和相对深度。比较识别出的裂纹参数与试件实际参数，计算两者之间的误差，表4给出了裂纹参数识别结果和误差。

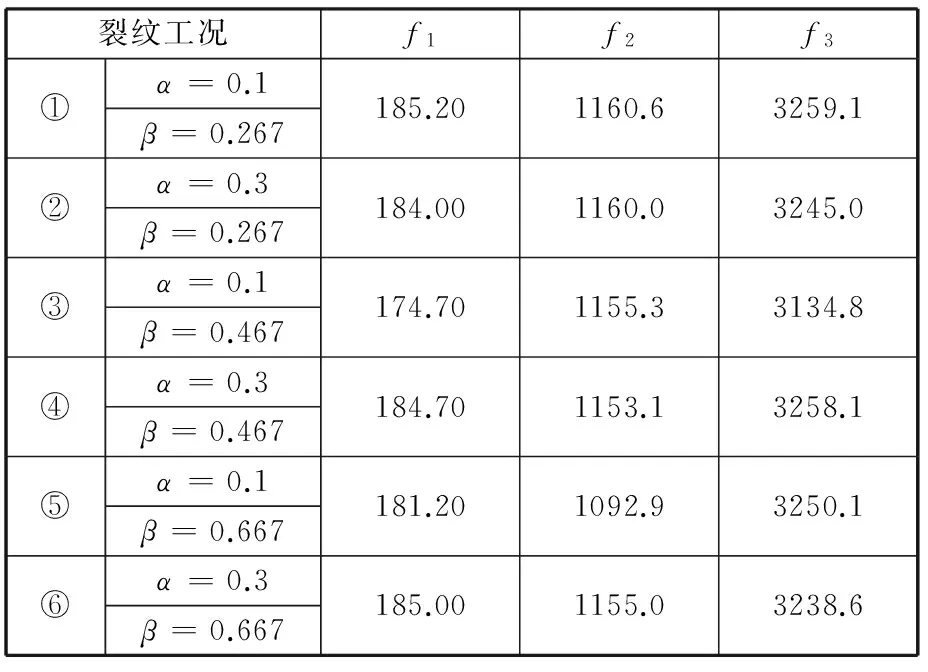
表3 实测6种工况条件下前三阶固有频率

由表4误差分析可知，实测固有频率下,除去工况⑥裂纹深度误为14.0%，其余均在7.0%以内；裂纹相对位置的识别误差不超过4.4%。对于横截面高度为20 mm、悬臂梁有效长度为300 mm的裂纹梁来说，裂纹深度识别误差在1.4 mm以内，裂纹位置的识别误差在13.2 mm以内。总的来说，裂纹参数识别精度较高，具有较好的工程应用前景。

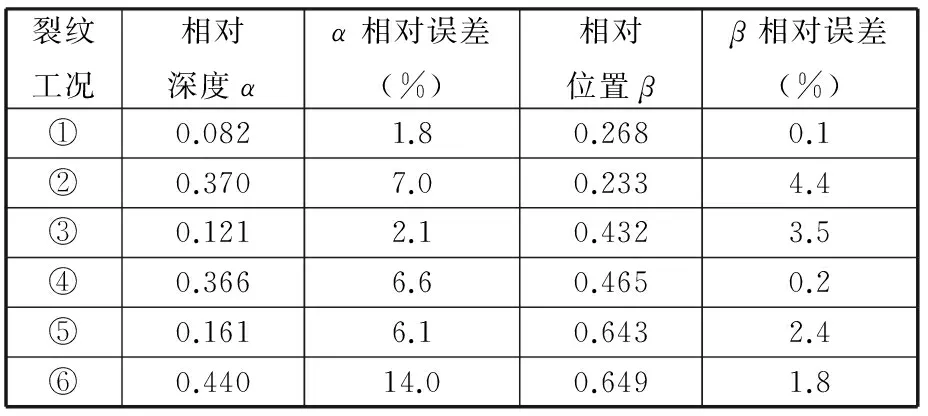
表4 等高线法悬臂梁裂纹参数识别结果2

4.3 误差分析与讨论

影响裂纹梁损伤识别精度的因素有很多，但是主要是正问题的求解精度和实测固有频率的测量精度。原因在于：

(1)如果通过呼吸裂纹梁固有频率方程构造的固有频率响应曲面精度很差，也就是裂纹模型的建立不可靠，则裂纹识别精度就难以保证。

(2)实测固有频率的精度影响因素分为内因和外因两种。内因是裂纹处于某阶次或某几阶次模态振型的节点处或在节点附近时，裂纹变化对梁的固有频率影响很小，几乎可以忽略，从而导致测量结果无法用于裂纹识别。外因主要是传感器引起的附加重量的影响、悬臂梁的悬臂边界难以模拟、模态测量仪器的测试精度等原因，容易造成固有频率测量误差。实测固有频率误差直接影响投影所得的固有频率等高线的准确性，进而影响若干等高线的交点位置，即影响了裂纹相对位置和相对深度等参数的识别效果。

(a)工况①

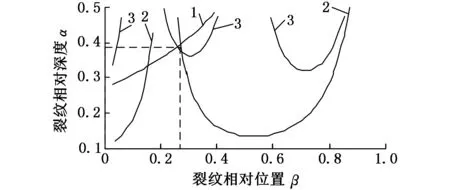
(b)工况②

(c)工况③

(d)工况④

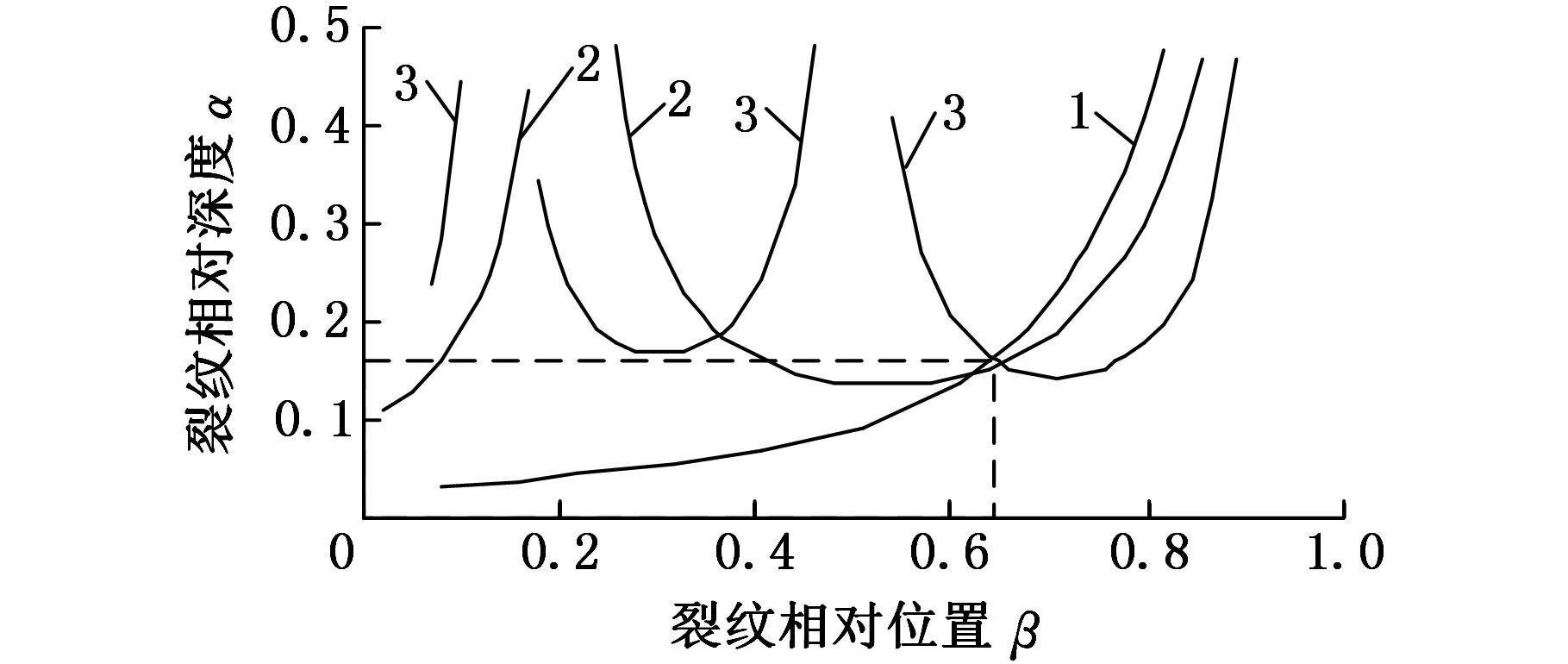
(e)工况⑤

(f)工况⑥1.第一阶固有频率等高线投影 2.第二阶固有频率等高线投影 3.第三阶固有频率等高线投影图4 裂纹参数识别2Fig.4 Case 2 of crack parameters identification

5 结论

(1)把呼吸式裂纹梁简化为由扭转弹簧连接的两段弹性梁，在假定振动响应随振幅变化的基础上推导出含呼吸裂纹梁的固有频率方程。

(2)考虑呼吸裂纹的开合情况，假定裂纹梁的刚度是振幅的非线性函数，建立了呼吸裂纹梁的多项式刚度模型。

(3)结合等高线裂纹识别理论和方法，提出了一种基于固有频率的呼吸裂纹梁损伤识别新方法。通过算例验证了方法的可行性与有效性，方法的识别精度取决于实验固有频率的精度。

[1] CADDEMI S, CALIO I. Exact Closed-form Solution for the Vibration Modes of the Euler-bernoulli Beam with Multiple Open Cracks[J]. Journal of Sound and Vibration， 2009, 327(1): 473- 489.

[2] CORNWELL P, DOEBLING S W, FARRAR C R. Application of the Strain Energy Damage Detection Method to Plate-like Structures[J]. Journal of Sound and Vibration, 1999, 224(2):359-374.

[3] STUBBS N, KIM J T, FARRAR C R. Field Verification of a Non-destruction Damage Localization and Sensitivity Estimator Algorithm[C]// Proceeding of the 13th International Modal Analysis Conference. Nashville, Tennessee, 1995:210-218.

[4] 刘文光,李俊,严铖，等.弹性梁损伤识别模态应变能法研究[J].中国机械工程,2014,25(12):1651-1654. LIU Weguang, LI Jun, YAN Chen, et al. Modal Strain Energy Method for Damage Detection of an Elastic Beam[J]. China Mechanical Engineering, 2014, 25(12):1651-1654.

[5] YANG X F, SWAMIDAS A S J, SESHADRY R. Crack Identification in Vibration Beams Using the Energy Method[J]. Journal of Sound and Vibration, 2001, 224(2):339-357.

[6] SWAMIDAS A S J, YANG X F, SESHADRY R. Identification of Cracking in Beam Structures Using Timoshenko and Euler Formulation[J].Journal of Engineering Mechanics, 2004, 130 (11) : 1297-1308.

[7] 吴国荣.含裂纹梁自由振动分析[J].船舶力学,2007,11(5):798-803. WU Guorong. Free Vibration Analysis of Crackedbeam[J].MechanicsofShip, 2007, 11(5):798-803.

[8]KSIAM,BRANDONJ.TheEffectsofClosureofCracksontheDynamicsofaCrackedCantileverbeam[J].JournalofSoundandVibration, 2000, 238(1):1-18.

[9]CHENGSM,WUXJ,WALLACEW,etal.VibrationalResponseofaBeamwithaBreathingCrack[J].JournalofSoundandVibration, 1999, 225(1):201-208.

[10]BOVSUNOVSKYAP,SURACEC.ConsiderationsRegardingSuper-harmonicVibrationofaCrackedBeamandtheVibrationintheDampingCausedbythePresenceoftheCrack[J].JournalofSoundandVibration, 2005, 288:865-886.

[11]ABRAHAMONL,BRANDONJA.ModelingoftheOpeningandClosureofaCrack[J].JournalofVibrationandAcoustics, 1995，117:370-377.

[12]ZHANGW,TESTARB.ClosureEffectonFatigueCrackDetection[J].EngineeringMechanics, 1999, 125(2):1125-1132.

[13]GMOAS.CrackDetectioninBeamsUsingChangesinFrequenciesandAmplitudesofFrequencyResponseFunctions[J].JournalofSoundandVibration, 2003, 265(1): 1-22.

[14]LEEYS,CHUNGMJ.AStudyonCrackDetectionUsingEigen-frequencyTestData[J].ComputersandStructures, 2000, 77(3): 327-342.

(编辑 苏卫国)

A Damage Identification Method of a Breathing Cracked Beam by Natural Frequency

LIU Wenguang GUO Longqing HE Honglin YAN Long

School of Aeronautic Manufacturing Engineering，Nanchang Hangkong University，Nanchang，330063

Firstly, a cracked cantilever beam was simplified into two elastic beams connected by a torsion spring. It was supposed that the vibration response varied as the vibration amplitude of the beam. And the natural frequency equation of a breathing cracked beam was derived. Then, the open and close conditions of the breathing crack during vibrations were considered. A polynomial stiffness model of the breathing cracked beam was built up by the postulation that the stiffness of the cracked beam was one of nonlinear functions of the vibration amplitudes. Thereafter, a damage identification method of a breathing cracked beam by natural frequency was proposed combined with the natural frequency equation and the stiffness model. The feasibility and effectiveness of this method was verified by case studies in the end. Results indicate that the identification precision of this method depends on the testing precision of the experimental natural frequency.

breathing crack; natural frequency; damage identification; contour method

2015-12-24

国家自然科学基金资助项目(51565039)

V215.4DOI：10.3969/j.issn.1004-132X.2017.06.011

刘文光，男，1978年生。南昌航空大学航空制造工程学院副教授、博士。主要研究方向为飞行器结构动力学及疲劳寿命预测。E-mail:liuwg14@163.com。郭隆清，男，1991年生。南昌航空大学航空制造工程学院硕士研究生。贺红林，男，1967年生。南昌航空大学航空制造工程学院教授、博士。颜 龙，男，1992年生。南昌航空大学航空制造工程学院硕士研究生。