基于递推最小二乘法与模糊自适应扩展卡尔曼滤波相结合的车辆状态估计
2017-04-07魏民祥赵万忠张凤娇严明月
汪 魏民祥 赵万忠 张凤娇,2 严明月
1.南京航空航天大学能源与动力学院,南京,2100162.常州工学院机械与车辆工程学院,常州,213002
基于递推最小二乘法与模糊自适应扩展卡尔曼滤波相结合的车辆状态估计
1.南京航空航天大学能源与动力学院,南京,2100162.常州工学院机械与车辆工程学院,常州,213002
针对汽车状态估计中模型参数的变化和观测噪声的时变特性,提出了递推最小二乘法与模糊自适应扩展卡尔曼滤波相结合的汽车状态估计算法。为实现模型参数与观测噪声的实时更新,建立了基于三自由度非线性车辆动力学模型的算法,首先利用递推最小二乘法对汽车的总质量进行估计,其次建立了模糊控制器对扩展卡尔曼滤波的观测噪声进行实时跟踪。在搭建的CarSim与MATLAB/Simulink联合仿真平台中验证了该算法的有效性,结果表明该算法估计精度高于传统扩展卡尔曼滤波算法,研究结果为汽车的主动安全控制提供了理论支持。
汽车总质量估计;状态估计;递推最小二乘法;模糊自适应扩展卡尔曼滤波
0 引言
随着汽车工业的飞速发展,汽车主动安全技术越来越受到人们的关注。对汽车主动安全的研究几乎都需要获知汽车的当前行驶状态,例如汽车的当前车速、侧向加速度、横摆角速度和质心侧偏角等重要参数。对于上述关键状态参数的获取,目前研究中用得较多的方法是软观测,即基于算法的估计[1]。
目前汽车状态估计器设计所采用的方法主要有扩展卡尔曼滤波(EKF)[2-3]、无迹卡尔曼滤波[4-5]、神经网络[6-7]、模糊逻辑[8]等,它们都是对汽车控制系统中的关键控制变量(包括质心侧偏角、侧向速度、横摆角速度等)进行估计。
但这些方法都是基于模型参数(汽车总质量)固定或算法参数(观测噪声协方差)固定来进行状态估计的,若参数改变将会导致结果精度降低,甚至可能会导致滤波发散。
为了提高基于非线性汽车动力学模型状态估计算法的鲁棒性与估计精度,本文提出一种递推最小二乘(recursive least squares,RLS)法与模糊自适应卡尔曼滤波(fuzzy adaptive extended Kalman filter,FAEKF)相结合的算法。
1 非线性汽车动力学模型
本文估计算法中将车辆视为多个刚体组合,基于理论力学建立车辆动力学模型并将其作为估计算法研究的对象。考虑建模的复杂程度和实时计算的需要,需引用纵向、侧向和横摆三个自由度的状态变量来进行估算,因此,在二自由度车辆模型的基础上引入一个纵向运动自由度,使该模型具有横摆、侧向和纵向三个自由度[9],模型简图见图1。

图1 三自由度车辆动力学模型Fig.1 3-DOF vehicle dynamics model
图1中,假设车辆是对称的,oxy是固定在车辆质心处的坐标系,x轴在汽车的纵向对称轴上,规定驾驶员的正向为x轴正方向;y轴在水平面内,与x轴垂直,通过车辆质心o点,规定驾驶员的左向为y轴正方向。其中,转向盘转角等于前轮转角与转向盘转角到前轮转角的传动比的乘积。对三自由度车辆模型建立方程如下:
(1)
(2)
(3)
(4)
式中,vx为纵向速度;r为横摆角速度;k1为前轮总侧偏刚度;k2为后轮总侧偏刚度;m为汽车总质量;a为前轴到质心的距离;b为后轴到质心的距离;δ为前轮转角;ax为纵向加速度;ay为侧向加速度;Iz为绕z轴的转动惯量;β为质心侧偏角。
2 基于RLS法的汽车总质量估计
RLS法是一种参数辨识方法,是最小二乘法的递推形式,适用于单输入单输出(single input single output, SISO)动态模型的在线参数辨识,采用该方法不需要已知任何先验统计特性,并且计算量小、收敛速度快[10]。为更好地估计汽车总质量,选择在汽车平稳行驶状态时进行估计,考虑实际情况,在底盘主动安全系统工作时,应当有较好的汽车状态估计输入,即总质量应最先辨识出来,故选择汽车起步工况进行参数辨识,此时可认为轮胎的侧偏特性处在线性范围,因此采用线性二自由度车辆模型[11]。汽车总质量辨识模型如下:
(5)
RLS输入输出递推方程如下[10]:
(6)
y(k)=φ(k)Tθ+e(k)
(7)
将式(6)改写成式(7),其中u(k)为输入;y(k)为输出;n为待辨识参数的总个数;e(k)为由观测噪声或建模引起的误差;θ为待估参数组成的向量,θ=(a1,a2,…,an,b1,b2,…,bn)T;φ(k)=[-y(k-1) … -y(k-n)u(k-1) …
u(k-n)]T。下面针对辨识模型(式(5)),令θ=(m),φ(k)=[ay],进行汽车总质量估计。
参数辨识增益:
K(k)=P(k-1)φ(k)[φ(k)TP(k-1)φ(k)+1]-1
参数辨识更新:
辨识误差更新:
P(k)=[I-K(k)φ(k)T]P(k-1)

3 模糊自适应扩展卡尔曼滤波
根据式(1)~式(4),建立状态空间方程:

(8)
其中,三维状态向量x(t)=(r,β,vx)T;一维输出向量y(t)=(ay);二维控制向量u(t)=(δ,ax)T;w(t)与v(t)是均值为零的白噪声,且互不相关。
将非线性函数f(x(t),u(t),w(t))、h(x(t),v(t))分别对状态x(t)求偏导,得到雅可比矩阵F(t)与H(t):
至此完成了模型线性化。
由于EKF是基于离散状态空间方程的算法,故采用前向欧拉法将车辆连续状态空间方程进行离散,得到相应离散系统的状态空间方程:
vx(k)=(r(k-1)β(k-1)vx(k-1)+
ax(k))Δt+vx(k-1)
其中,Δt为采样时间步长。观测矩阵如下:
传统的EKF算法在滤波计算中,假设观测噪声协方差矩阵已知且固定不变。在汽车行驶过程中,传感器的噪声水平受不同的工况和外界环境的影响,传统估计算法设定观测噪声协方差矩阵不变,这会影响EKF的估计精度。为此,建立一个模糊控制器对观测噪声协方差矩阵进行实时调整,使EKF算法具有自适应性。
离散状态空间方程为
xk+1=Fkxk+Bkuk+wk
zk=Hkxk+vk
下面给出离散的EKF估计过程。
状态一步预测:
一步预测误差方差阵:
增益矩阵:
状态更新:
方差更新:
Pk=(I-KkHk)Pk|k-1

取实际方差:
理论方差:
令方差的差值
e=Pa-Pt
(25)

e={NB,NM,NS,Z,PS,PM,PB}

U={PVS,PS,PSM,PM,PSB,PMB,PB,PVB}
其中,NB为负大,NM为负中,NS为负小,Z为零,PS为正小,PM为正中,PB为正大,PVS为正的高等偏小,PSM为正的中等偏小,PSB为正的初等偏大,PMB为正的中等偏大,PVB为正的高等偏大。其输入输出隶属函数如图2~图4所示,模糊规则如表1所示。

图2 输入e的隶属函数Fig.2 Membership function of Input variable e
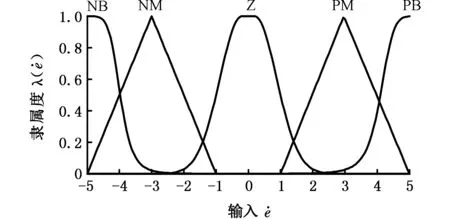
图3 输入的隶属函数

图4 输出U的隶属函数Fig.4 Membership function of Input variables U

表1 模糊规则
定义k时刻观测噪声协方差的估计值为Rk,Rk=UR。通过模糊控制器不断改变Rk的值达到EKF算法的自适应。
4 基于虚拟实验的算法验证
4.1 汽车总质量的估计验证
在CarSim与MATLAB/Simulink环境下建立联合仿真平台。选择普通前驱D级Sedan车型进行仿真,整车的参数如表2所示。设定车辆速度为60 km/h。
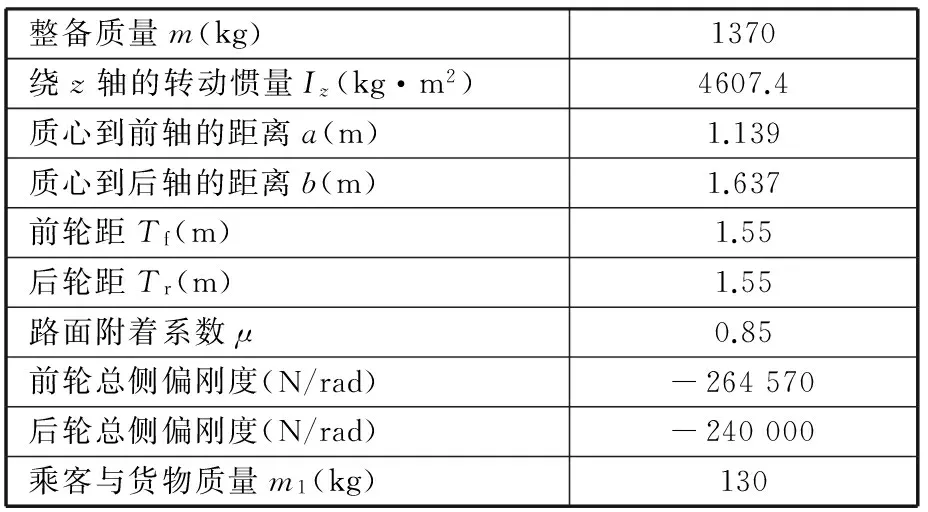
表2 整车参数
仿真设定在固定附着系数为0.85的良好路面进行蛇行试验,前轮转角变化如图5所示,在1~2 s内转角为零,在2~8 s内转角呈幅值为10、周期为2 s的正弦变化,在8~10 s内转角为零。纵向加速度变化值如图6所示,由CarSim软件输出作为算法的输入。

图5 前轮转角变化图Fig.5 The change of front wheel angle
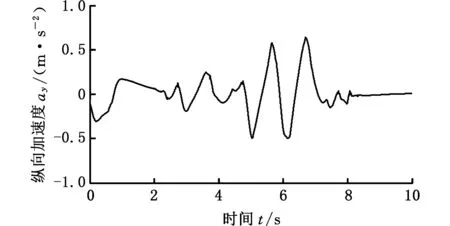
图6 纵向加速度变化图Fig.6 The change of longitudinal acceleration
汽车总质量初值设为1000 kg,实际值为1500 kg,基于RLS算法的汽车总质量估计仿真结果如图7所示。

图7 基于RLS的汽车总质量的估计值based on RLS与实际值的对比Fig.7 Comparison between estimates and actual value of total vehicle quality estimation
由图7可知,基于RLS算法估计的汽车总质量在初值为1000 kg的条件下能较快跟踪到实际值,在9 s内能实现实际值的良好跟踪,且在之后波动很小,最大偏差为23 kg,相对误差为1.53%,此精度完全满足控制要求。考虑实际情况,当整车总质量发生变化时,在正常驾车情况下,总是汽车先停车,然后上下人员或者装卸货物;当汽车重新由停止状态启动而进入加速行驶的过程中,程序又会自动重新估计汽车总质量,作为状态估计的输入,因此,当汽车总质量发生变化(即模型参数变化)时,算法的状态输入能很好地跟踪汽车总质量的变化。由图7可知,RLS较好地估计了汽车的总质量,这为后续汽车状态估计奠定了基础。
4.2 汽车关键状态估计验证
将CarSim软件的状态输出结果作为实际值,将RLS与FAEKF相结合的算法估计结果,与EKF算法估计结果和实际值进行对比,以验证本文优化算法的有效性。
在状态估计过程中,不论是EKF算法还是RLS与FAEKF结合的算法,它们的过程噪声协方差矩阵的值都固定不变且相同,即Q=diag(0.1,0.1,0.1)。EKF算法的观测协方差矩阵值也固定不变, EKF观测协方差矩阵值R=[0.001]。EKF算法的汽车总质量为整备质量,即为1370 kg。RLS与FAEKF结合的算法观测协方差初值Rk=[0.001],且随着时间的推移,观测协方差Rk发生变化,变化规律如表3所示。FAEKF+RLS算法的汽车总质量为RLS的估计值,仿真时间为10 s。汽车关键状态估计结果如图8~图10所示。

表3 观测噪声协方差变化规律

图8 纵向车速估算对比图Fig.8 Comparison of longitudinal vehicle speed estimation
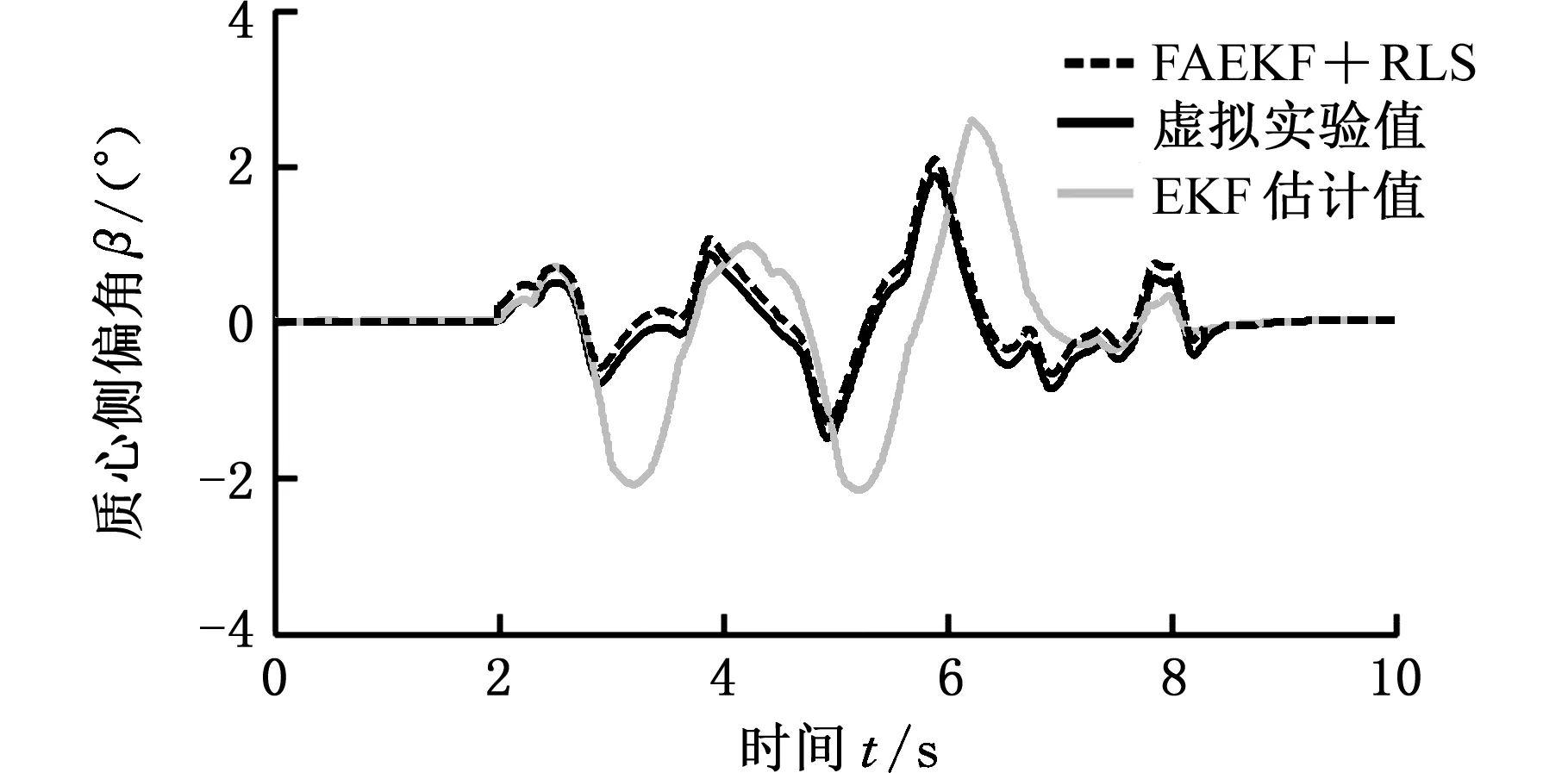
图9 质心侧偏角估算对比图Fig.9 Comparison of sideslip angle estimation
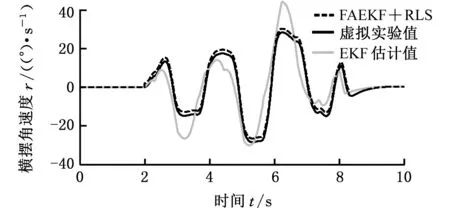
图10 横摆角速度估算对比图Fig.10 Comparison of yaw rate estimation
图8是EKF算法与FAEKF+RLS算法对纵向车速的估计值与实际值的对比图。可以看出,FAEKF+RLS算法的纵向车速估计值与实际值一直很接近,估计效果比较理想,估计值与实际值最大瞬态偏差只有0.08m/s,相对误差为0.04%;而EKF算法的估计值与实际值的最大瞬态偏差为0.36m/s,相对误差为2.1%。在整个仿真时间内EKF算法估计值偏差较大的主要原因是:没有实时估计汽车总质量,以整备质量代替汽车总质量;观测协方差已更新,而EKF仍然按固定的观测方差进行循环计算,导致偏差较大。在2~8s内偏差越来越大,主要是由于给定观测协方差越来越大。在0~2s与8~10s内EKF的观测方差值与动态给定值相同,所不同的是,车速估计值在0~1s内有较大下降趋势,而在8~10s内估计值与实际值接近。这种差异是输入量纵向加速度的变化导致的,在图6中0~1s内纵向加速度急剧下降且为负值,即减速行驶造成EKF估计值比实际值低,在8s以后加速度基本接近零,使得EKF估计值与实际值偏差较小。
图9中,EKF算法的估计值与实际值最大瞬态偏差为0.83°,相对误差为63.8%;FAEKF+RLS算法的估计值与实际值最大瞬态偏差为0.03°,相对误差为1.76%。
图10中,EKF算法估计值与实际值最大瞬态偏差为27.3(°)/s,相对误差为108%;FAEKF+RLS算法的估计值与实际值最大瞬态偏差为1.4(°)/s,相对误差为4.6%。从图9、图10中可以看出,质心侧偏角与横摆角速度的EKF算法估计值、FAEKF+RLS算法估计值与实际值相比,在0~2s与8~10s内偏差都很小,主要是观测协方差相同。这与纵向速度在0~2s内与实际值偏差较大的情况比较,区别在于纵向速度直接与纵向加速度有关,而横摆角速度与质心侧偏角间接相关,具体函数关系见式(1)~式(3)。在2~8s内,由于以整备质量代替汽车总质量,以及观测协方差发生改变且变动越来越大,所以造成EKF算法估计值的偏差越来越大,FAEKF+RLS算法由于对汽车总质量进行实时估计且对观测方差及时更新,使得估计值与实际值偏差很小。以上分析说明本文算法估计效果良好。
5 结论
(1)本文提出将RLS算法与FAEKF算法相结合进行车辆状态估计,使估计误差大大减小,达到与汽车总质量恒定且观测噪声为定值状态下的估计精度相当的效果。
(2)虚拟实验结果表明,RLS算法和FAEKF算法相结合可以很好地跟踪虚拟实验值,优于单纯的EKF算法,具有较好的精度和鲁棒性。
[1] 张凤娇,魏民祥,赵万忠. 基于蚁群优化UKF算法的汽车状态估计[J].中国机械工程,2015,26(22) :3046-3050.ZHANGFengjiao,WEIMinxiang,ZHAOWanzhong.VehicleStateEstimationBasedonAntColonyOptimizationAlgorithm[J].ChinaMechanicalEngineering, 2015,26(22):3046-3050.
[2]WENZELTA,BURNHAMKJ.DualExtendedKalmanFilterforVehicleStateandParameterEstimation[J].VehicleSystemDynamics, 2007, 42(2):153-171.
[3] 宗长富,胡丹,杨肖,等. 基于扩展Kalman滤波的汽车行驶状态估计[J]. 吉林大学学报(工学版),2009,39(1): 7-11.ZONGChangfu,HUDan,YANGXiao,etal.VehicleDrivingStateEstimationBasedonExtendedKalmanFilter[J].JournalofJilinUniversity(EngineeringandTechnologyEdition), 2009, 39(1): 7-11.
[4]ANTONOVS,FCHNA,KUGIA.UnscentedKalmanFilterforVehicleStateEstimation[J].VehicleSystemDynamics, 2011,49(9):1497-1520.
[5] 赵又群,林棻.基于UKF算法的汽车状态估计[J].中国机械工程,2010,21(5):615-619.ZHAOYouqun,LINFen.VehicleStateEstimationBasedonUnscentedKalmanFilterAlgorithm[J].ChinaMechanicalEngineering, 2010, 21(5): 615-619.
[6]MCLZIS,SABBIONIE.OntheVehicleSideslipAngleEstimationthroughNeuralNetworks:NumericalandExperimentalResults[J].MechanicalSystemsandSignalProccssing, 2011,25(6):2005-2019.
[7] 张小龙,李亮,李红志,等.基于改进RBF网的汽车侧偏角估计方法试验研究[J].机械工程学报,2010,46(22) : 105-110.ZHANGXiaolong,LILiang,LIHongzhi,etal.ExperimentalResearchonVehicleSideslipAngleEstimationBasedonImprovedRBFNeuralNetworks[J].ChineseJournalofMechanicalEngineering, 2010, 46(22): 105-110.
[8] 施树明,LUPKCRH,BREMMERP, 等.基于模糊逻辑的车辆侧偏角估计方法[J].汽车工程,2005,27(4):426-430.SHIShuming,LUPKERH,BREMMERP,etal.EstimationofVehicleSideSlipAngleBasedonFuzzyLogic[J].AutomotiveEngineering, 2005, 27(4): 426-430.
[9] 武钟财. 基于扩展卡尔曼滤波的路面附着系数估计算法研究[D]. 长春:吉林大学,2008.WUZhongcai.ResearchontheAlgorithmoftheRoadFrictionCoefficientEstimatiomBasedontheExtendedKalmanFilter[D].Changchun:JilinUniversity, 2008.
[10] 蔡季冰. 系统辨识[M]. 北京: 北京理工大学出版社,1989: 25-34.CAIJibing.SystemIdentification[M].Beijing:BeijingInstituteofTechnologyPress,1989: 25-34.
[11] 余志生.汽车理论[M]. 5版. 北京:机械工业出版社,2012 :144-146.YUZhisheng.VehicleDynamics[M]. 5thed.Beijing:MechanicalIndustryPress, 2012:144-146.
(编辑 王旻玥)
Vehicle State Estimation Based on Combined RLS and FAEKF
WANG Yan1WEI Minxiang1ZHAO Wanzhong1ZHANG Fengjiao1,2YAN Mingyue1
1.College of Energy and Power Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing,210016 2.School of Mechanical &Vehicle Engineering,Changzhou Institute of Technology, Changzhou,Jiangsu,213002
For the problems of observation noise time-varying characteristics and model parameter variations in vehicle state estimation, a new algorithm which consisted of RLS method and FAEKF was proposed. The new algorithm was proposed based on 3-DOF nonlinear vehicle dynamics model in order to realize real time update of model parameters and observation noises. Firstly, the total mass of the vehicle was estimated by RLS. Then, a fuzzy controller was established to track the observation noises of extended Kalman filters. Finally, the algorithm was verified using CarSim and MATLAB/Simulink. Results show that the estimation accuracy of the new algorithm is higher than that of the traditional extended Kalman filter. It may provide theoretical support for the development of automobile active control systems.
automobile total quality estimation; state estimation; recursive least squares(RLS); fuzzy adaptive extended Kalman filter(FAEKF)
2016-08-09
国家自然科学基金资助项目(51375007);江苏省自然科学基金资助项目(SBK2015022352);常州市科技计划应用基础研究项目(CJ20159011)
U461.6DOI:10.3969/j.issn.1004-132X.2017.06.019
汪,男,1992年生。南京航空航天大学能源与动力学院硕士研究生。主要研究方向为汽车电子安全控制技术。E-mail:1305905618@qq.com。魏民祥,男,1963年生。南京航空航天大学能源与动力学院教授、博士研究生导师。赵万忠,男,1982年生。南京航空航天大学能源与动力学院教授。张凤娇,女,1978年生。常州工学院机械与车辆工程学院副教授,南京航空航天大学能源与动力学院博士研究生。严明月,女,1992年生。南京航空航天大学能源与动力学院硕士研究生。
