基于组合机器学习算法的软件缺陷预测模型

傅艺绮 董 威 尹良泽 杜雨晴

(国防科学技术大学计算机学院 长沙 410073) (fu_303503@163.com)

基于组合机器学习算法的软件缺陷预测模型

傅艺绮 董 威 尹良泽 杜雨晴

(国防科学技术大学计算机学院 长沙 410073) (fu_303503@163.com)

软件缺陷预测是根据软件产品中提取的度量信息和已经发现的缺陷来尽早地预测软件可能还存在的缺陷，基于预测结果可合理分配测试和验证资源.基于机器学习的缺陷预测技术能够较全面地、自动地学习模型来发现软件中的缺陷，已经成为缺陷预测的主要方法.为了提高预测的效率和准确性，对机器学习算法的选择和研究是很关键的.对不同的机器学习缺陷预测方法进行对比分析，发现各算法在不同评价指标上有不同的优势，利用这些优势并结合机器学习中的stacking集成学习方法提出了将不同预测算法的预测结果作为软件度量并进行再次预测的基于组合机器学习算法的软件缺陷预测模型,最后用该模型对Eclipse数据集进行实验，表明了该模型的有效性.

软件缺陷预测；机器学习；集成学习；组合；Eclipse预测数据集

随着软件逐渐深入人们的生活，软件质量成为人们关注的重点.软件缺陷是影响软件质量的重要因素，它在软件的开发过程中是不可避免的，但若不能及时发现并处理，可能会使软件发生故障无法使用，甚至产生严重的后果.最常用的软件质量保证活动就是软件测试，它能有效检查软件的错误，但同时也是软件开发生命周期中花费时间、资源最多的阶段.因此出现缺陷预测的概念，旨在根据软件的基本属性(复杂度、规模、开发过程等)来尽早地预测软件可能还遗留的缺陷，并基于预测结果合理分配测试资源，给出测试的优先级，提高软件产品质量，缩短开发周期，降低开发成本.

当前的缺陷预测技术主要分为静态预测和动态预测两大类.静态预测是基于缺陷相关的度量数据，对缺陷的数量和分布进行预测；动态预测则是对故障随时间的分布进行预测.2005年以来，机器学习方法被越来越多地用于软件缺陷预测模型的建立，通过从以往的开发经验中抽取带有问题领域特征的数据来进行学习，建立起数据与软件缺陷之间的关联关系，并对未知的软件模块预测其可能的缺陷数量或发生缺陷的可能性.在基于机器学习技术的缺陷预测模型研究中，一般解决3个问题：1)哪些机器学习方法适合建立预测模型；2)哪些度量元适合缺陷预测；3)哪些指标用于评估模型[1].

机器学习包含多种学习方法，如人工神经网络(artificial neural network, ANN)、贝叶斯网络(Bayesian network, BN)、决策树(decision tree, DT)、随机森林(random forest, RF)等.Khoshgoftaar等人[2]比较了7种不同的预测模型，这些模型用到了不同的回归和分类树算法，如C4.5，CHAID，CART等；Fenton等人[3]提出用贝叶斯信念网络预测软件缺陷模块的方法；Vandecruys等人[4]比较了一些常用的学习方法，包括C4.5、支持向量机(support vector machine, SVM)、逻辑回归、K-最近邻等，发现C4.5的预测准确度最高，但在其他评价指标上这些方法不分伯仲；Turhan和Bener[5]分析了朴素贝叶斯方法在缺陷预测上的应用，认为同基于决策树、线性回归、判别分析、神经网络的软件缺陷预测模型相比较，贝叶斯方法能够获得更显著的性能提升；常成成[6]引入集成学习的概念，提出了一种基于Adaboost自适应增强算法的缺陷排序预测方法，弱学习机选用SVM，该算法结合Adaboost的优势，在学习中重点关注被错误分类的实例，最终获得预测效果良好的强分类器；文献[7]使用Adaboost算法改进神经网络算法，将多个弱预测器组成新的强预测器，改善模型预测精确度和泛化能力；文献[1]认为不同的建模技术的预测性能表现出的差异较小，而不同度量元的选择对预测性能的影响更加显著；用于建立预测模型的度量元主要分成代码度量、复杂性度量、面向对象度量、过程度量和历史缺陷度量几大类，Hall等人[8]以预测的精确度和召回率作为评价指标，认为基于面向对象度量元的预测模型比基于复杂性度量元的模型效果更好，综合使用多类度量元的预测模型效果显著提高，而用过程度量元进行预测效果却差强人意；文献[9]选用排序能力和分类能力作为缺陷预测模型的评价标准，并引入了工作量评价指标，对这些度量元的缺陷预测能力进行了比较分析，认为在不同的数据集下不同种类度量的预测能力不存在绝对的优劣关系，而大多数情况下，代码度量和过程度量的缺陷预测性能较好.

在实际应用中，代码度量能从一个软件系统当前版本的源代码中轻松得到，而过程度量和历史缺陷度量的收集成本昂贵，需要从版本控制系统和缺陷追踪系统提取.因此本文主要针对构建模型的方法问题提出了一种基于组合机器学习算法的缺陷预测改进模型，将不同机器学习算法的预测组合起来，把第1次预测的结果作为新的度量元加入数据集后进行第2次预测，同时运用特征选择方法，提高缺陷预测的效率.为了表明模型的实用性，论文对Eclipse标准数据集进行了缺陷预测，验证了本文方法的有效性.

Fig. 1 Software defects prediction model图1 软件缺陷预测模型

1 基于机器学习的缺陷预测模型

本节将简单介绍缺陷预测与机器学习的相关概念.缺陷预测是从软件模块中提取合适的度量元数据，并由机器学习的分类、回归、聚类等方法找出缺陷与度量元之间的关系，建立起相应的模型，预测新的软件模块是否含有缺陷或预测缺陷的分布，模型如图1所示[10]：

根据预测的目的可将缺陷预测模型分为2类：1)分类问题的软件缺陷预测，即预测软件模块是否含有缺陷；2)排序问题的软件缺陷预测，预测软件模块的缺陷数目，并根据缺陷的多少给出模块的排序.本文将针对不同的机器学习算法的组合对缺陷预测的分类与排序问题分别进行研究.

1.1 缺陷预测模型

1.1.1 分 类

基于分类问题的软件缺陷预测的目的是预测软件模块是否含有缺陷，引导软件开发人员将测试资源集中在预测为有缺陷的模块.针对此类缺陷预测模型出现了大量的研究成果，预测效果良好，但仍然无法完全正确预测所有软件模块.当错误地将非缺陷模块预测为有缺陷时，会引起测试资源的浪费；当错误地将有缺陷的模块预测为无缺陷时，则存在缺陷不能及时发现与修复的风险.出现这2种错误的代价并不相同，如何平衡二者，找出更适合的软件缺陷预测模型一直是研究的重点.

1.1.2 排 序

基于排序问题的缺陷预测模型适合测试资源未知的情况——将软件模块按缺陷数目进行排序，优先测试含缺陷个数多的软件模块，当测试资源富余的时候，可以继续对含缺陷少的模块进行测试.对于此类缺陷预测模型，很难做到精准地预测软件模块所含的缺陷个数，关键是对软件模块给出高质量的排序结果.目前排序问题的软件缺陷预测模型的主要构造算法是利用机器学习中的回归算法.

1.2 机器学习算法

决策树算法[11]是一种常见的用于分类的建模方法，通过构造决策树来发现数据中蕴含的分类规则.当应用决策树建立缺陷预测模型时，需要在预测变量的缺值处理、剪枝技术、派生规则等方面作相应改进，同时还应避免出现过度拟合问题，尽量减少路径的长度，以提高预测模型的性能.

线性回归是利用多个自变量的最优组合共同来预测或估计因变量，比只用一个自变量进行估计更有效，也更符合实际.线性回归是最基础的用于排序问题的回归算法，通过建立软件度量元与缺陷数目之间的线性方程来计算未知模块可能含有的缺陷数目.逻辑回归是线性回归的一种改进技术，采用对数变换将线性回归的结果映射为0-1之间的值，因此对于预测软件是否有缺陷的二分类问题能够容易地建立模型.

贝叶斯分类器基于贝叶斯定理，是建立在特征独立性假设基础上的简单的统计学习分类器，它理想地认为对于给定的类变量，一个给定的特征不依赖于其他的特征.贝叶斯分类器只需要很少的训练样本来对预测模型的参数进行估计，在特征属性完全独立或属性之间相关关系不太明显的情况下有比较好的性能.贝叶斯网络是一种不确定性因果关系模型，具有强大的不确定性处理问题能力，能有效地进行多元信息表达与融合，可广泛地用于故障预测.

人工神经网络是一种模仿动物神经网络行为特征、进行分布式并行信息处理的计算模型.大多数情况下，人工神经网络能基于外界信息改变内部结构，是一种自适应系统.常用的多层感知机是使用标准BP算法训练的神经网络，是一种非线性统计性数据建模工具，常用来对输入与输出间复杂的关系进行建模，或用来探索数据的模式，是解决大复杂度问题的一种相对简单有效的方法.

除此之外，还有支持向量机、聚类分析等方法可以用于软件缺陷预测，都需要用历史数据来构建预测模型并验证，各技术间的优劣取决于数据自身以及它们在准确性、稳定性、泛化程度上的比较和分析.

2 基于机器学习的缺陷预测模型

2.1 提出问题

有研究指出，机器学习算法的选择对于提高缺陷预测模型的效果并不十分理想，由于数据集的差异性，预测性能最好的机器学习算法也在发生变化.我们对Eclipse数据集分别进行了分类预测和排序预测，其中分类预测用到了决策树、逻辑回归、贝叶斯网络和神经网络多层感知机算法；排序预测运用了随机森林、线性回归和神经网络多层感知机算法.通过分析发现，在不同的评价指标下，最优的机器学习算法不完全相同.对于分类问题，逻辑回归算法的预测精确率稍好于其他算法，而对于召回率指标，则是贝叶斯网络算法较好.对比综合评价指标，认为复杂的网络结构学习算法——贝叶斯网络和神经网络的缺陷预测模型的综合效果更好，但复杂度大，预测的时间开销显著增加，尤其是对数据集较大，度量元较多的情况.

因此我们设想：能否将不同机器学习算法结合起来构建缺陷预测模型，综合各机器学习算法的优点，在各项评价指标上都取得一定的改进效果，并提出了2个假设：

1) 组合的机器学习算法构建的软件缺陷预测模型对于分类问题有一定的提高；

2) 组合的机器学习算法构建的软件缺陷预测模型对于排序问题有一定的提高.

2.2 基于组合的机器学习算法的缺陷预测模型

本节将详细描述我们提出的基于组合机器学习算法的缺陷预测模型.

2.2.1 数据预处理

将从不同数据源收集到的数据整合成数据集，数据中可能存在数据冗余、数据缺失、错误的数据等问题，引入这些数据可能会导致缺陷预测模型的不准确，因此需要对数据集做清洗.另外，对于分类问题，还需要将数据集中的缺陷数目离散化，转化为缺陷的有无，故将缺陷数目大于0的看作有缺陷的一类，置为1；缺陷数目等于0的看作无缺陷，置为0.将处理后的数据集分成2部分：1)用于学习模型，也叫训练集;2)用于测试与验证，称为测试集.由于软件缺陷符合“2-8”原则，80%的软件缺陷集中在20%的软件模块中，因此收集到的数据中包含软件缺陷的模块数比不含缺陷的模块数要少得多，造成了数据集的极大不平衡，而根据这个不均衡样本集学习出来的模型将偏向于多数类而忽视少数类，即更倾向于将不含缺陷的模块正确分类.因此我们采用人工合成新样本的重采样策略来对不平衡数据集进行优化，使得含缺陷的数据与不含缺陷的数据在相同的数量级上，然后在此分布均衡的样本集上进行学习.

2.2.2 组合预测模型

在机器学习中，提高分类器性能的一种有效技术是集成学习[12]，就是将多种算法结合起来，这些算法可以是相同的，也可以是不同的.利用集成技术构造软件缺陷模型仍处于初级阶段，应用较广泛的是Bagging和Boosting集成算法，将多个弱预测器组成新的强预测器，改善模型预测精确度和泛化能力.本文借鉴另一种著名的集成学习技术——Stacking——的思想来构建模型.Stacking方法由Worlpert于1992年提出[13]，主要利用高级的基础学习器结合低级的基础学习器来获得更好的预测准确性，它与Bagging和Boosting方法的最大区别是Stacking方法并不是简单地结合同一类型的基础学习器，而是采用不同的机器学习算法构造学习器.Stacking框架包含2层分类器，level-0为基分类器；level-1为元分类器.基分类器由训练集以bootstrap采样的方式来构造，然后将基分类器的输出结果作为元分类器的输入，即训练集.元分类器的任务就是合理组合输出集，纠正基分类器的分类错误，以正确分类目标.因此组合预测的第1步便是用基础学习器对数据集进行预测，然后将基分类器的输出结果作为元分类器的输入，即将数据集输出的预测信息和训练数据的真实分类结果整合为一个数据集，然后，将新的数据集作为新学习器的训练数据集，再采用一种学习算法来解决这个问题.

这里，我们把Stacking方法的思想用于对软件缺陷进行预测.首先对训练集中的数据用简单的机器学习算法做一个快速的分类或排序预测，分类问题可用逻辑回归算法、决策树算法；排序问题可用线性回归算法、随机森林算法等.尽管此时数据集较大，运用的度量元较多，依然能够很快地得到结果.我们将预测结果写入原始的数据集作为一个新的度量元.由于预测的效果普遍良好，因此该预测结果与软件模块的真实缺陷数有较高的相关性.

运用较复杂的网络结构算法如贝叶斯网络、神经网络等对新的数据集进行第2层预测.由于建立模型的过程非常复杂，时间开销非常大，因此我们考虑采用特征选择技术来对数据降维，挑选出最优的属性子集运用到学习中，在尽量少的丢失信息的情况下提高模型性能，减少开销.同时，特征选择技术也可以解决度量数据集中存在的错误数据和某些度量与构建缺陷预测模型无关的问题.信息增益(information gain)和信息增益率(information gain ratio)都可以用于属性选择，我们的模型通过计算增益率来选择度量属性.

定义1. 属性A的信息增益率.IGR(A)=IG(A)I(A),其中IG(A)即属性A的信息增益：IG(A)=entropy(S)-entropy(S,A)，是未划分前的数据的熵与根据属性A划分后的数据集的熵的差值.

假设训练集S={S1,S2,…,SN}，其中Si包含一个属性向量Xi=(xi1,xi2,…xip)及分类标签ci∈C={c1,c2,…,cm).在缺陷预测中Xi和ci分别代表一个模块的度量向量和模块是否存在缺陷的标记.设pi是S中属于类别i的比例，则信息熵的计算方法：

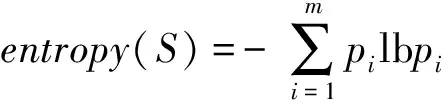
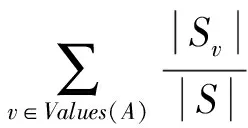
最后，将预先准备的测试集输入此模型，得到预测结果，将预测结果与真实的缺陷值进行比较评估，验证模型的有效性.当训练集与测试集来自同一个数据集时，我们采用10折交叉算法进行验证，即将数据集平均分成10份，轮流取其中9份作为训练数据，剩下1份作为测试数据，算出每一轮的准确率、召回率等评价指标.该实验重复10次进行，最终算出10次的平均值作为最终验证结果.

2.2.3 评价指标

对于分类模型，研究采用传统的分类器性能评价指标，包括精确度、召回率、F-度量、AUC等.我们可以将预测的结果用一个混淆矩阵表示,如表1所示：

Table 1 Confusion Matrix

1) 精确度：precision=TP(TP+FP);

2) 召回率：recall=TP(TP+FN);

3) F度量：F_measure=2×precision×recall(precision+recall);

4)AUC(area under ROC curve)：ROC曲线下面积.ROC曲线原本是用于描述收益和成本之间的权衡关系，我们以Y轴表示真正率，X轴表示真负率.AUC的范围在[0，1]，面积越大，模型越好.

对于排序问题，我们采用了Alberg图(CLC)作为评价指标，CLC是Ohlsson和Alberg[14]提出的衡量排序任务的软件缺陷预测模型的指标，它以模块的百分比为横坐标，累计的模块缺陷数的百分比为纵坐标.模型曲线下的面积越大越好.我们还运用了Arisholm等人[10]提出的CE(cost effectiveness)指标来评价.CE指标建立在基于代码行的Alberg图的基础上，和Alberg图类似，区别在于X轴表示排序后的模块累计的代码行数的百分比.每个模型的预测结果对应图2中的1条曲线.其中最优模型是按照软件的真实缺陷数排序后的结果，随机模型是指软件模块的排序完全随机，这2条曲线可以作为缺陷预测模型性能比较的基准，预测模型的曲线越接近最优模型则效果越好.

Fig. 2 CE cruve图2 CE曲线

3 实验与分析

3.1 实验准备

1) 实验环境

本实验在Intel Core i3-4130 3.40 GHz CPU，4 GB内存的PC机上完成，在Eclipse上编程开发，外部依赖项有weka.jar.

2) 实验数据

本实验数据来自Eclipse标准数据集[15]，其中有6个ARFF格式的文件，分别收集了Eclipse源码在package级别和file级别的度量元和缺陷数目，涉及Eclipse2.0，2.1，3.0这3个版本.数据集中所含的度量元包括：

1) Name——每条数据对应的文件名或包名；

2) Pre-release Defects——该版本发布前6个月内收集的缺陷数目；

3) Post-release Defects——该版本发布后6个月内收集的缺陷数目；

4) 复杂性度量——包括CK度量元和面向对象度量元，在表2中列出；

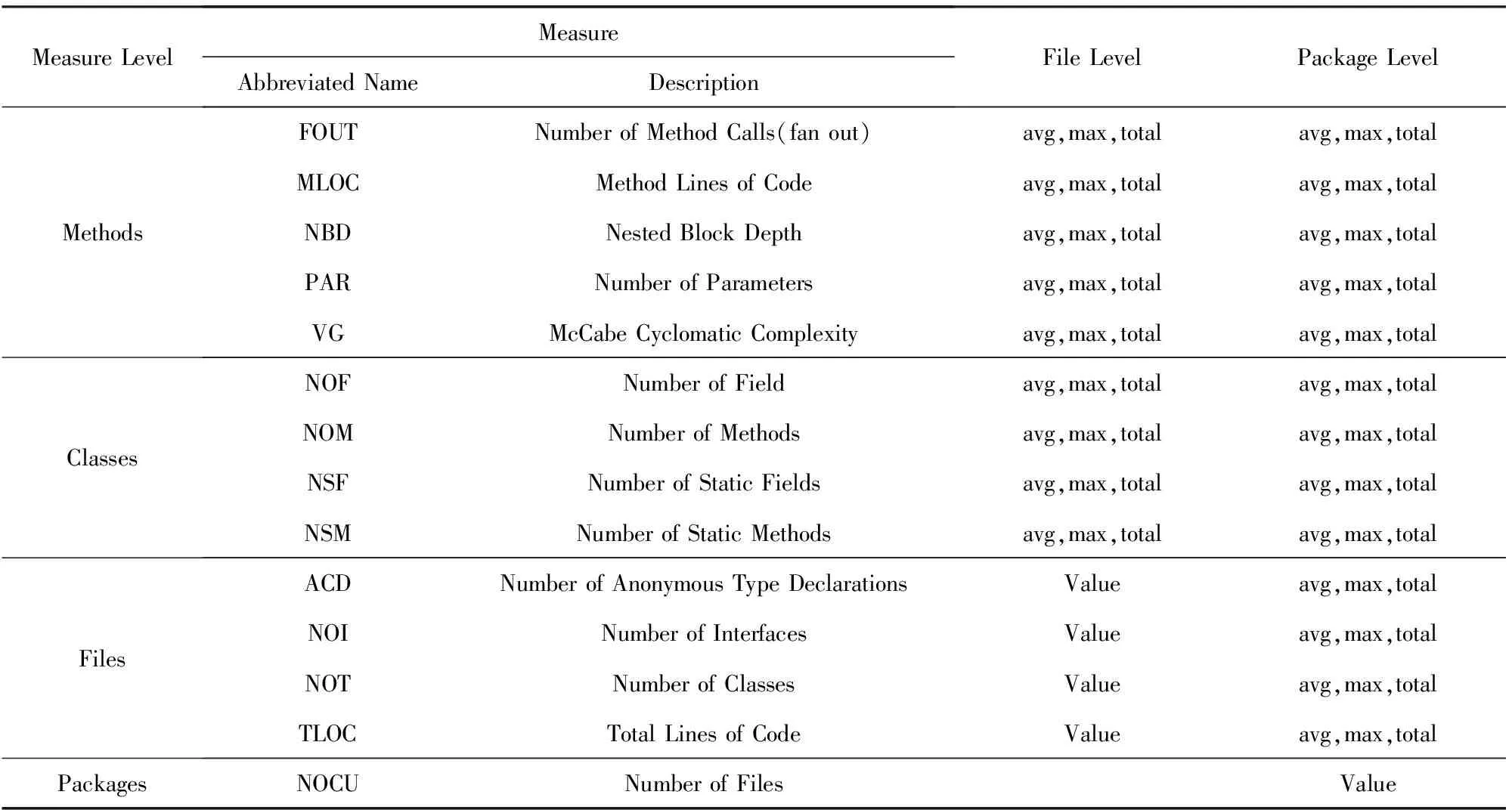
Table 2 Complexity Metrics of Eclipse Dataset

5) 抽象语法树结构——抽象语法树的结点度量.

由于File级别的数据集和Package级别的数据集在结构上存在差异，因此用File级别数据训练的模型只能用来预测File级别的数据，Package级别的同理.我们每次取其中一个版本的FilePackage数据来学习模型，分别预测3个版本的FilePackage数据，并且在训练集和测试集来自同一个版本时采用10折交叉验证，故利用Eclipse数据集全部文件可进行18次预测与验证.

3.2 实验结果

3.2.1 分类预测

首先对数据集进行简单算法的一次预测，由于实验结果过多且效果相似，故只列出部分实验结果，如表3所示.为了表示简便，使用J48代表决策树算法，LR代表逻辑回归，BN代表贝叶斯网络，NN代表神经网络.

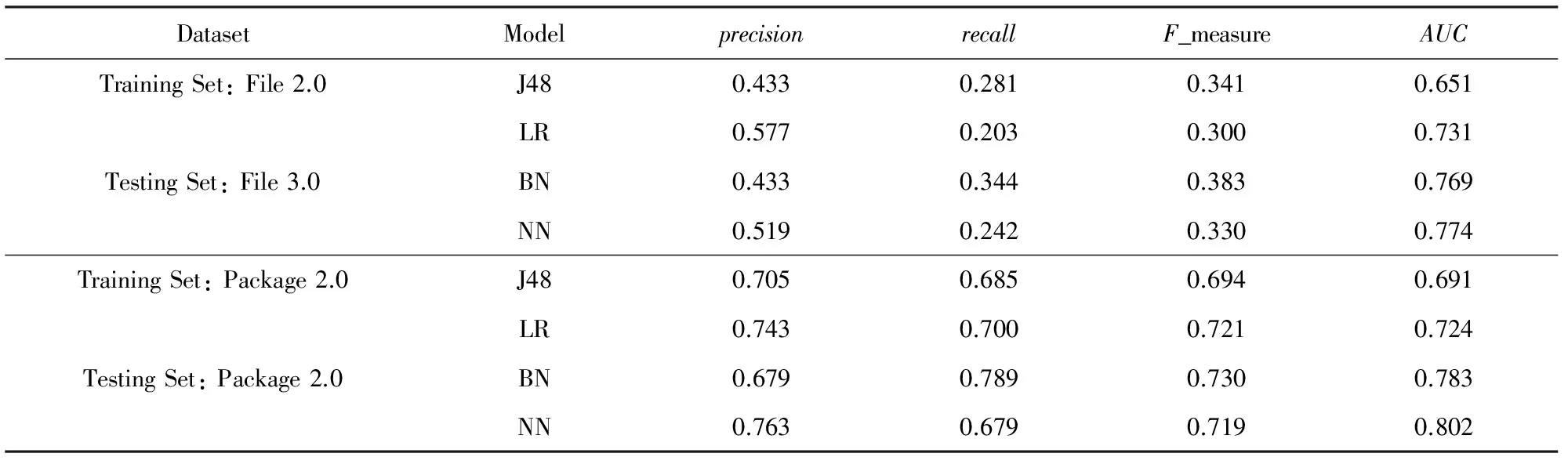
Table 3 Partial Results of Different Machine Learning Model

从表3看出逻辑回归算法虽预测精确度较好，但召回率在几种算法中偏低，综合评价模型的F_measure与AUC指标也较低，而复杂的网络模型的综合指标令人满意，但预测花费的时间太多.对于简单预测，全部18次实验可以在2 min内完成，而对于复杂算法全部完成18次实验需要数小时，其中File级别的预测由于数据量大而占了大部分.这就证实2.1节提到的对于不同的评价指标而言最优的算法不尽相同.

将决策树和逻辑回归的预测结果分别加入数据集，根据2.2节的描述构建组合模型，预测并加以验证，结果如表4所示.发现在训练集和测试集来自不同数据集时，将决策树预测结果加入度量元用组合模型预测的效果与单独用决策树预测的效果相近，分析原因可能是由于决策树预测的精确度不高，将许多实际有缺陷的数据错分为无缺陷的数据，因此将其结果加入数据集会影响模型的正确分类；而训练集与测试集来自同一数据集时的预测结果显示出现了过度拟合.逻辑回归结果加入数据集再进行组合预测，对大部分评价指标都有一定的提高效果，尤其是最关注的precision比单一预测的结果均要好，并且时间开销有了很大程度的减少，可以在30 min内完成全部预测.另外，所有实验在Package级别均比在File级别要好，是因为Package级别的测试集中有缺陷和无缺陷的数据数量上相差不大，数据集近似平衡.

Table 4 Partial Results of Combined Machine Learning Model

表5中列出了文献[15]对Eclipse数据集进行分类预测的结果，由于Zimmermann等人之后对Eclipse数据集做了一定的清洗，本文使用的Eclipse数据集与文献[15]所用的数据集略有不同，File级别的数据中有缺陷的数据占整个数据集的10%～15%，而文献[15]中有缺陷的数据占23%以上，由于本文学习所用到的缺陷数据较少，可能导致该预测模型没有充分学习到缺陷数据与软件度量元之间的关系，预测时产生了较多的分类错误，致使组合预测算法的precision不及表5中所示.但对于本文用到的Package级别的数据，有缺陷的数据占整个数据集50%左右，与文献[15]数据相近，比较precision和recall评价指标可以看出基于组合学习算法的预测具有明显优势.

Table 5 Prediction Result of Ref [15]

因此我们认为，本文提出的基于组合的机器学习算法构建的缺陷预测模型能够在一定程度上提高模型的各项评价指标，且比单一的机器学习算法有一定的优势.

3.2.2 排序预测

首先对数据集进行简单算法的一次预测，由于实验结果过多且效果相似，故只列出部分实验结果.用到的算法有随机森林、线性回归和神经网络.从图3可以看出这3种算法建立的模型在排序上的效果相同，实际试验中线性回归和随机森林构建的模型结构较简单，运算速度更快，而神经网络的时间开销非常大，完成18次实验需要数小时.

根据本文提出的组合机器学习算法得到新的预测模型，并按照预测结果的值从大到小将模块排序，做出CLC曲线和CE曲线，如图4所示.在CLC评价下，加入线性回归度量的神经网络预测模型有一定的提高，CE指标和单个算法预测类似.然而改进的空间不大，分析原因是由于所选用的3种机器学习算法的效果相似，不能为组合模型的正确预测提供更多有用的信息，且每种机器学习算法的CE结果曲线均接近斜率为1的直线，即接近随机排序的结果，推测该数据集对排序的预测不能取得良好的效果.

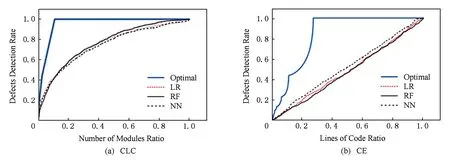
Fig. 3 Results of different machine learning model (File 2.0 as training Set, File 2.1 as testing Set)图3 不同机器学习模型的部分预测结果(训练集为File 2.0、测试集为File 2.1)

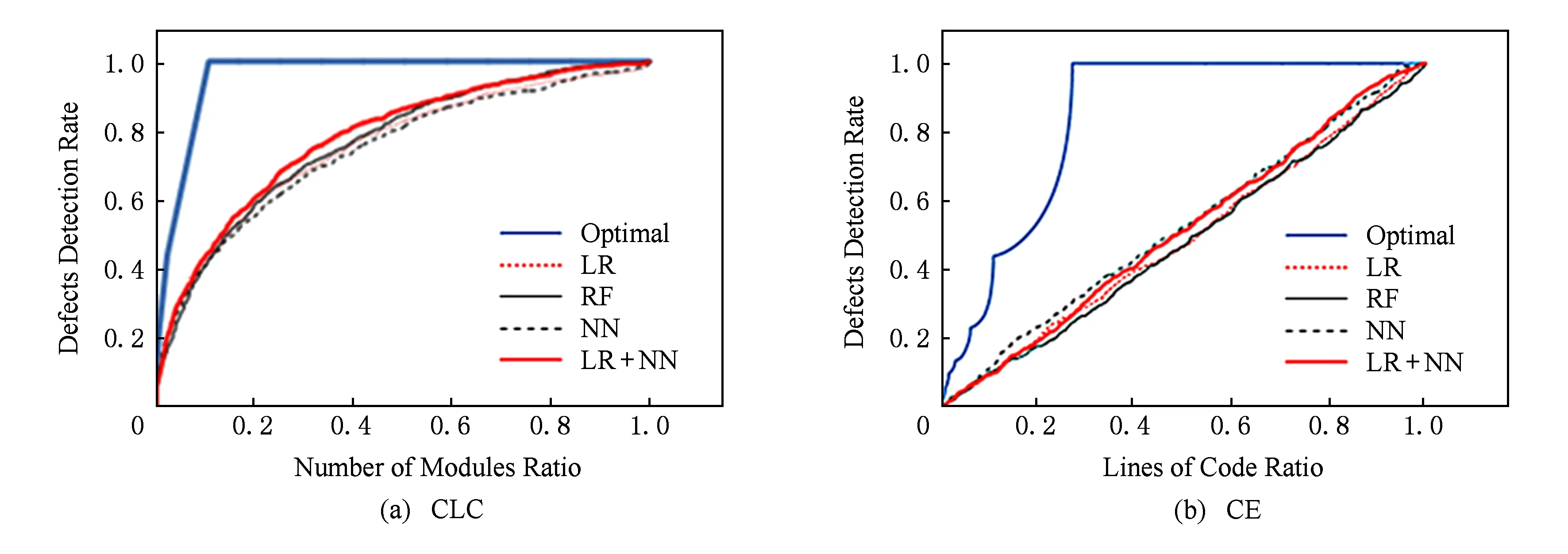
Fig. 4 Results of combined machine learning model (File 2.0 as training set, File 2.1 as testing set)图4 组合机器学习模型的部分预测结果(训练集为File 2.0、测试集为File 2.1)

4 总结与展望

本文针对当前软件缺陷预测模型中机器学习算法对预测模型性能的影响问题，提出了一种基于不同机器学习算法的组合来建立缺陷预测模型的方法，首先对原始数据集进行一次快速预测，将该预测的结果加入数据集作为一个新的度量元，再对新数据集进行属性选择、降维，再通过鲁棒性更强的复杂机器学习算法来构建新的模型并用于预测，得到的预测模型在缺陷预测的分类和排序问题上都有一定的效果.然而第1层预测的结果对该模型的影响较大，应尽量选择准确度较高的学习算法，否则加入新的度量元可能引入过多的错误数据，导致缺陷预测模型向着错误的方向构建.如何更好地组合不同的学习算法使它们更紧密的联系在一起，如何进一步提高缺陷预测模型的性能指标以及考虑过程度量等其他类型的度量数据是下一步将研究的问题.

[1]Arisholm E, Briand L C, Johannessen E B. A systematic and comprehensive investigation of methods to build and evaluate fault prediction models[J]. Journal of Systems and Software, 2010, 83(1): 2-17

[2]Khoshgoftaar T M, Seliya N. Comparative assessment of software quality classification techniques: An empirical case study[J]. Empirical Software Engineering, 2004, 9(3): 229-257

[3]Fenton N, Krause P, Neil M, et al. A probabilistic model for software defect prediction[J]. IEEE Trans on Software Engineering, 2001, 44(21): 444-453

[4]Vandecruys O, Martens D, Baesens B, et al. Mining software repositories for comprehensible software fault prediction models[J]. Journal of Systems and Software, 2008, 81(5): 823-839

[5]Turhan B, Bener A. Analysis of Naive Bayes' assumptions on software fault data: An empirical study[J]. Data & Knowledge Engineering, 2009, 68(2): 278-290

[6]Chang Chengcheng. Research about software defect priority prediction model based on AdaBoost-SVM algorithm[D]. Nanjing: Nanjing University of Posts and Telecommunications, 2013 (in Chinese)(常成成. 基于AdaBoost-SVM的软件缺陷优先级预测模型的研究[D]. 南京: 南京邮电大学, 2013)

[7]Li Xiang, Zhu Quanyin. Prediction of improved BP neural network by Adaboost algorithm[J].Computer Engineering & Science, 2013, 35(8): 96-102 (in Chinese)(李翔, 朱全银. Adaboost算法改进BP神经网络预测研究[J]. 计算机工程与科学, 2013, 35(8): 96-102)

[8]Hall T, Beecham S, Bowes D, et al. A systematic literature review on fault prediction performance in software engineering[J]. IEEE Trans on Software Engineering, 2012, 38(6): 1276-1304

[9]Zhao Hongyuan. Using effort-aware performance indicators to compare the ability of code metrics, process metrics, and historical fault metrics to predict fault-proneness[D]. Nanjing: Nanjing University, 2013 (in Chinese)(赵宏远. 代码度量、过程度量和历史缺陷度量: 工作量感知的缺陷预测能力比较[D]. 南京: 南京大学, 2013)

[10]Wang Pei. Research on software defect prediction based on feature selection[D]. Wuhan: Central China Normal University, 2013 (in Chinese)(王培. 特征选择在软件缺陷预测技术中的应用研究[D]. 武汉: 华中师范大学, 2013)

[11]Keene S E. A programmer’s guide to object-oriented programming in common LISP[M]. Reading, MA: Addison-Wesley, 1988

[12]Schwenker F. Ensemble methods: Foundations and algorithms [book review][J]. Computational Intelligence Magazine, 2013, 8(1): 77-79

[13]Wolpert D H. Stacked generalization[J]. Neural Networks, 1992, 5(2): 241-259

[14]Ohlsson N, Alberg H. Predicting fault-prone software modules in telephone switches[J]. IEEE Trans on Software Engineering, 1996, 22(12): 886-894

[15]Zimmermann T, Premraj R, Zeller A. Predicting defects for Eclipse[C]Proc of the 3rd International Workshop on Predictor Models in Software Engineering. Piscataway, NJ: IEEE, 2007: 9

Fu Yiqi, born in 1992. Master. Her main research interests include defects prediction and high confidence software technology.

Dong Wei, born in 1976. PhD, professor and PhD supervisor. Member of CCF. His main research interest include program analysis and high confidence software technology.

Yin Liangze, born in 1986. PhD. Member of CCF. His main research interest include model checking and high confidence software technology.

Du Yuqing, born in 1991. Master. Her main research interest is high confidence software technology.

Software Defect Prediction Model Based on the Combination of Machine Learning Algorithms

Fu Yiqi, Dong Wei, Yin Liangze, and Du Yuqing

(CollegeofComputer,NationalUniversityofDefenseTechnology,Changsha410073)

According to the metrics information and defects found in a software product, we can use software defect prediction technology to predict more defects that may also exist as early as possible, then testing and validation resources are allocated based on the prediction result appropriately. Defect prediction based on machine learning techniques can find software defects comprehensively and automatically, and it is becoming one of the main methods of current defect prediction technologies. In order to improve the efficiency and accuracy of prediction, selection and research of machine learning algorithms is the critical part. In this paper, we do comparative analysis to different machine learning defect prediction methods, and find that different algorithms have both advantages and disadvantages in different evaluation indexes. Taking these advantages, we refer to the stacking integration learning method and present a combined software defect prediction model. In this model, we first predict once, then add the prediction results of different methods in the original dataset as new software metrics, and then predict again. Finally, we make experiments on Eclipse dataset. Experimental results show that this model is technical feasibility, and can decrease the cost of time and improve the accuracy.

software defect prediction; machine learning; ensemble learning; combination; Eclipse prediction dataset

2015-12-09；

2016-06-30

国家“九七三”重点基础研究发展计划基金项目(2014CB340703)；国家自然科学基金项目(91318301，61690203) This work was supported by the National Basic Research Program of China (973 Program) (2014CB340703) and the National Natural Science Foundation of China(91318301, 61690203).

董威(wdong@nudt.edu.cn)

TP311