基于GPU的约束网络模型和并行弧相容算法
2017-04-07李占山
李 哲 李占山 李 颖
(吉林大学计算机科学与技术学院 长春 130012) (符号计算与知识工程教育部重点实验室(吉林大学) 长春 130012)(zslizsli@163.com)
基于GPU的约束网络模型和并行弧相容算法
李 哲 李占山 李 颖
(吉林大学计算机科学与技术学院 长春 130012) (符号计算与知识工程教育部重点实验室(吉林大学) 长春 130012)(zslizsli@163.com)
弧相容算法是约束满足问题的基本压缩求解空间算法之一,很多优秀的高级算法都以高性能的弧相容算法作为核心.近年来,以GPU为计算工具加速并行计算被用来尝试解决许多问题.基于GPU和基本的并行算法,提出一种适合GPU运算的约束网络表示模型N-E,给出其生成算法BuildNE.结合细粒度的弧相容算法——AC4,基于N-E模型提出AC4的并行化算法AC4GPU与改进算法AC4GPU+,使弧相容算法得以扩展到GPU上执行.实验结果验证了该算法的可行性,与AC4算法的比较,其在一些规模较小的问题上取得了10%~50%的加速,在一些规模较大的问题上则加速1~2个数量级.为今后进一步在GPU上以并行形式解决其他约束满足问题提供了一种核心算法方案.
人工智能;约束满足问题;弧相容;图形处理器;计算统一设备架构
约束满足问题(constraint satisfaction problem, CSP)[1]是人工智能领域的一个重要分支,现实生活中的很多问题,都可以约束建模转化为约束满足问题,使用约束求解技术进行求解.如生产调度问题、路由选择问题、产品配置问题、诊断等.众所周知,弧相容(arc consistency, AC)是最著名的约束传播算法之一,是求解约束满足问题的核心,在维持弧相容(maintain arc consistency, MAC)算法中广泛使用,也是执行单弧相容(singleton arc consistency, SAC)算法[2]的底层算法,它确保每个变量值域中的每个值与每个约束是相容的.Mohr和Henderson[3]在1986年提出了AC4[4],是第1个细粒度的弧相容算法,已经证明AC4具有最优的时间复杂度.
伴随多核的硬件大量出现,并行理论迅速发展,逐渐产生出一大批并行算法,通过对原有算法的并行化或者提出全新的并行算法都大幅提升了算法的性能.从早先Nguyen[5],Yokoo等人[6]提出利用分布式来解决特定的约束满足问题,到 Campeotto等人[7]利用混合CPU和GPU进行约束传播,在某些测试用例上取得了优势.很多学者对并行约束满足问题进行了尝试,涵盖并行、分布式[5-7]、多核、GPU等方向[8-9].图形处理器(GPU)由于在处理大规模的并行计算领域的优点,给计算领域带来巨大变革.现有的GPU并行计算框架,如CUDA,OpenCL,C++ AMP等已建立起一套成熟的编程模型,可以用来快速地解决目标问题.
推理和搜索是处理约束满足问题的2种技术,现有基于GPU的约束满足问题的研究主要集中在搜索方向,通过细粒度的GPU级别的并行机制处理约束传播[8];而在推理方向的研究则较少,以现有的弧相容算法为例,它们大都基于串行的思想提出,难以在大规模细粒度的并发程序中取得令人满意的效果.本文尝试采用推理的方法对约束网络的转化问题进行研究,提出将约束网络转换为更易于并行算法的新模型——N-E模型;并参考AC4算法,提出在该模型上基于GPU运行的并行弧相容算法AC4GPU及其改进算法AC4GPU+,进而分析了GPU并行算法的特点.最后实验结果表明:这2个算法在一些规模较小的问题较之AC4取得了10%~50%的加速,在一些规模较大的问题上,取得了1~2个数量级的性能提高,并为单弧相容算法和求解约束满足问题提供了一种新的可行底层算法.
本文提出的在GPU上解决弧相容的方案包括3部分:
1) 提出一种约束网络(constraint network)在GPU上表示的模型——N-E模型;
2) 提出基于GPU创建N-E模型的并行算法BuildNE;
3) 提出在N-E模型上基于GPU的细粒度弧相容算法AC4GPU及其的改进算法AC4GPU+.
1 背景知识
定义1. 变量和约束.变量(variable)[10]是具有不同取值的对象.变量x拥有与其相关联的论域,用dom(x)表示,该论域包括被x允许值的集合,dominit(x)表示初始时(未删除变量值前)变量x的论域.约束(constraint)[10]是定义在变量集合上的关系.一个约束c表示变量取值之间的制约关系,c所包含的变量是整个变量集合的子集,用scp(c)表示;与c相关联的关系用rel(c)表示.
定义2. 约束网络[1].约束网络P=(X,C),其中X={x0,x1,…,xn-1}是n个变量的集合,C={c0,c1,…,ce-1}是e个约束的集合.
给定约束网络P,对于任意c∈C,满足|scp(c)|=2,我们称该约束网络为二元约束网络,若存在c∈C,满足|scp(c)|>2,则称该网络为多元约束网络,多元约束网络可以转化为等价的二元约束网络.因此,二元约束满足问题一直是该领域研究的热点,本文主要讨论二元约束满足问题.
定义3. 弧相容[4,10].对于任意约束网络P=(X,C),弧相容可以被递归定义如下:
1) 1个点(x,a)是弧相容的,当且仅当在每一个包含x的约束c中,都存在(x,a)的支持,其中c∈C,x∈scp(c),a∈dom(x);
2) 1个变量x是弧相容的,当且仅当∀a∈dom(x),(x,a)是弧相容的;
3) 1个约束网络P是弧相容的,当且仅当该网络的每一个变量都是弧相容的.
例1. 图1(a)所示为一个简单的二元约束网络P=(X,C),其中:
1) 变量集合X={x1,x2,x3};
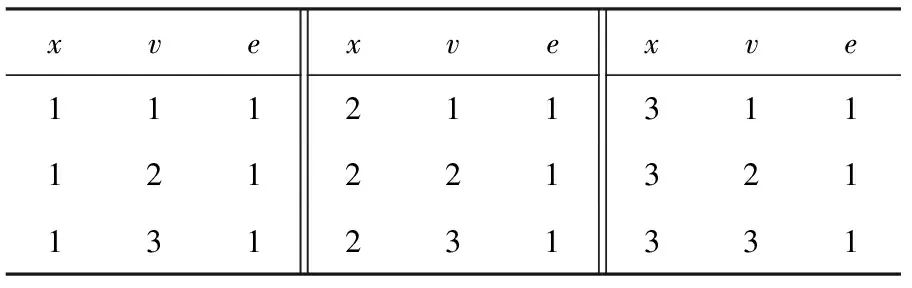
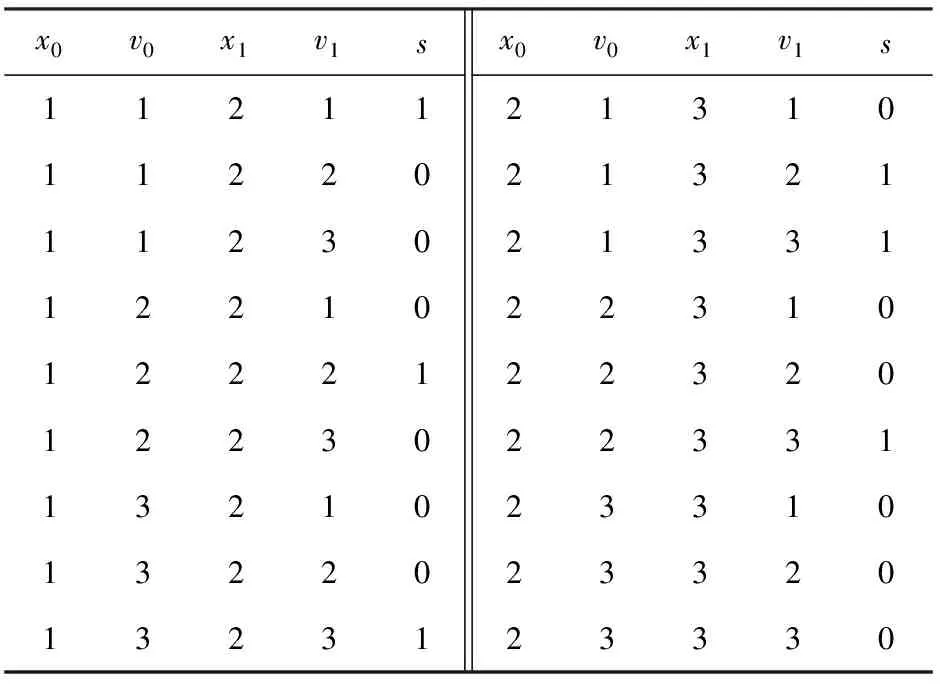
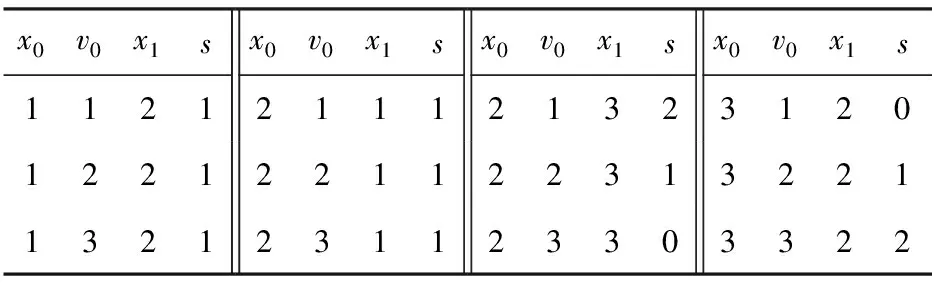
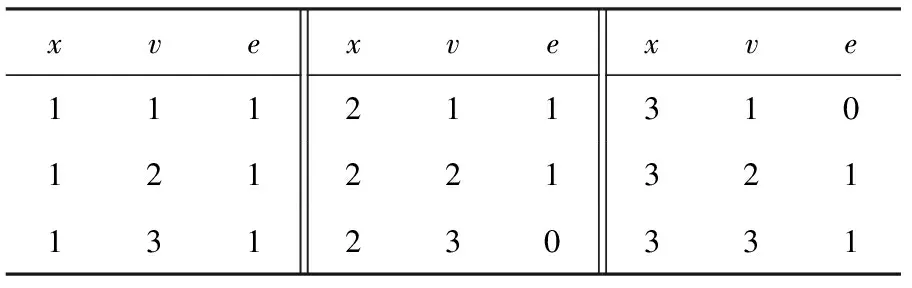
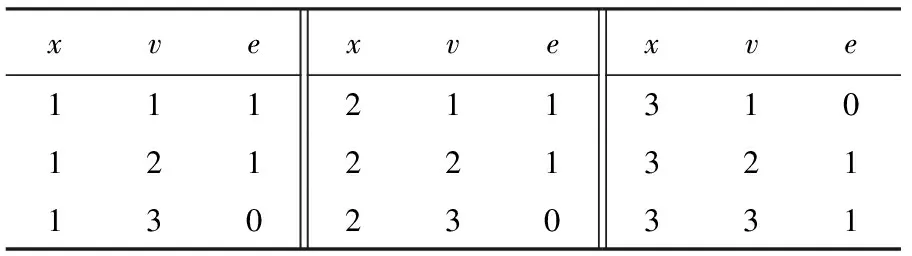
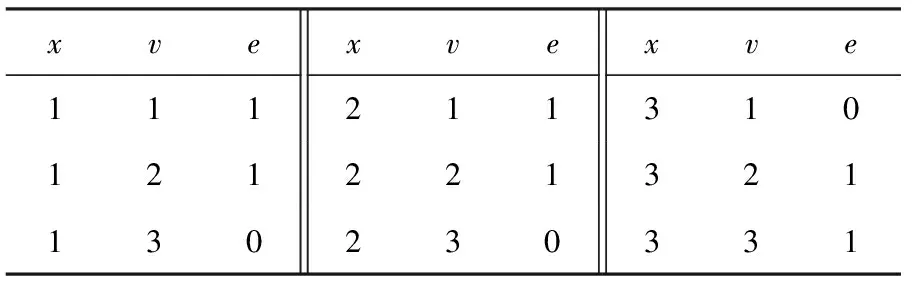
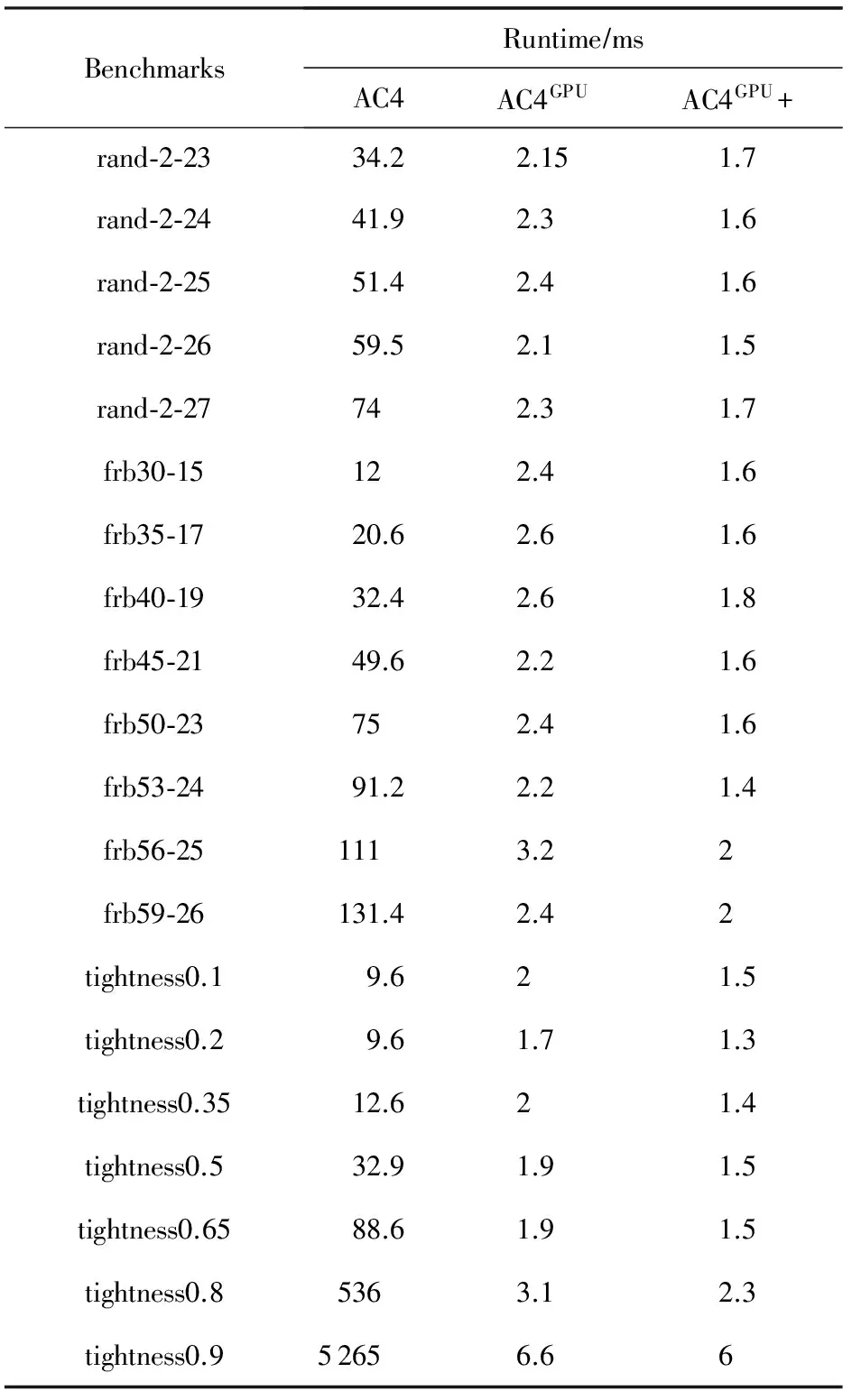
2) 约束集合C={c1,c2},c1:x1=x2,c2:x1 图1(b)删去了约束网络P中不满足弧相容的点,此时整个约束网络P满足弧相容. Fig. 1 Binary constraint network图1 二元约束网络 1.1 AC4 AC4是Mohr和Henderson[3]在1986年提出的一种弧相容算法.该算法分为2个阶段:初始化阶段和传播阶段. 1) 初始化阶段计算计数器counter[xi,vi,xj],其中xi,xj∈ci j,vi∈dom(xi),表示根据约束ci j包含的一个变量xi中的点(xi,vi)在另一个变量xj上的支持数.算法同时根据ci j建立由(xi,vi)支持的所有点的列表S[xi,vi].本阶段在约束集合上执行所有可能的约束检查,每当点(xi,vi)在ci j上找到1个支持vj∈dom(xj).计数器counter[xi,vi,xj]加1,同时(xi,vi)被加到S[xi,vi]列表中.若在某约束上一个点在另一个变量的论域中没有支持时,此时对应counter三元组的值为0,算法就将这个点从论域中删去,并放入队列Q中,等待在传播阶段中进行约束传播. 2) 传播阶段针对Q中每个待删除的点(xj,vj),为每一个点(xi,vi)∈S[xj,vj]的计数器counter[xi,vi,xj]减1.若counter[xi,vi,xj]减到0,表明(xi,vi)在变量xj没有支持,(xi,vi)被放入队列Q中.当Q为空时表明没有不相容的点存在,达成弧相容.若在删点过程中发现某一变量论域为空,则不相容. 算法1. AC4. 输入:P=(X,C); 输出:P满足AC输出真,反之输出假. ①Q←∅;S[xi,vi]←∅,vj∈dom(xj),∀xj∈X; ② foreachxi∈X,ci j∈C,vi∈dom(xi) do ③ 初始化counter[xi,vi,xj] to |{vj∈ dom(xj)|(vi,vj)∈ci j}|; ④ ifcounter[xi,vi,xj]=0 then ⑤ 删除(xi,vi)并将之加入Q中; ⑥ end if ⑦ 将(xi,vi)加入S[xj,vj]中s.t.(vi,vj)∈ci j; ⑧ ifdom(xi)=∅ then ⑨ return false; ⑩ end if 2.1 归 约 定义4. 归约(reduce).归约[11-12]是一类基本的并行算法,对传入的O(n)个输入数据,使用一个满足结合率的二元运算⊕,生成1个结果.归约是其他高级算法中重要的基础算法. 例2. 由满足结合律的二元运算⊕连接的8个元素的归约结果可以用如下形式表示: 由于该运算满足结合律,故其输入元素可以任意顺序进行二元计算.图2展示了处理8元素数组的不同方式.为了方便对比,我们在图2(a)中给出了串行实现,现在只需要具备可以计算⊕操作的计算单元,完成计算需要执行7步,性能较差. 在例2并行执行的过程中(如图2(b)(c)),步骤1并发启动4个线程计算相邻或交替的2个元素,将计算结果写入内存中;步骤2启动2个线程计算第1步的结果;步骤3再启动1个线程计算步骤2得到的2个结果.假设不考虑线程启动的代价,对数步长的归约得到计算结果只需要O(logn)步(这里是3步). Fig. 2 Reduction of set elements图2 集合元素的归约 按键归约(reduce by key)对于一组用〈k,v〉形式表示的键值对序列: {〈k0,v00〉,…,〈k0,v0m〉,〈k1,v10〉,…, 〈k1,v1l〉,…,〈kp,vp0〉,…,〈kp,vp n〉}. 对具有相同键(key)的若干值(value)进行归约求和,其结果为 对于输入规模为O(n)的数组,对其进行按键归约操作的最坏步骤复杂度为O(logn). 2.2 扫 描 扫描(scan)[12-13],或称前缀扫描(prefix scan)、前缀求和(prefix sum)、并行前缀求和(parallel prefix sum)是并行编程的重要术语,并作为基本模块用于许多不同算法. 定义5. 扫描.扫描可以分为包容性扫描(inclusive scan)和排他性扫描(exclusive scan)两种情况.对传入的n个输入数据{a0,a1,…,an-1},使用满足结合率的二元运算⊕,生成输出序列: {a0,(a0⊕a1),…,(a0⊕a1⊕…⊕an-1)}, 称为包容性扫描(inclusive scan). 现定义恒等式元素I,使得I⊕a=a,生成输入序列: {I,a0,(a0⊕a1),…,(a0⊕a1⊕…⊕an-2)}, 称为排他性扫描(exclusive scan). 可以看出,包容性和排他性扫描可以通过添加或删去输入数组的元素而相互转化. 流压缩(stream compaction)是根据一定标准筛选数组元素的操作,对输入序列{a0,a1,…,an-1}的每个元素建立判定P,用来判定对应输入元素是否应该包含在输出数组中,这些判定P按顺组成判定序列{P0,P1,…,Pn-1},对此判定序列执行1次排他性扫描计算出满足条件的输入元素在输出数组的位置.对于输入数据空间复杂度为n的数组,流压缩的步骤复杂度为O(logn). 2.3 CUDA编程技术 计算统一设备架构(compute unified device architecture, CUDA)是显卡厂商NVIDIA推出的并行计算架构.该架构通过利用GPU的并发处理能力,可大幅提升计算性能. NVIDIA提供一套完整的CUDA编程模型[12],通过编程语言的接口访问GPU的计算和存储资源.内核(kernel)是在GPU上执行的程序,问题可以被分成若干部分,以线程块的形式被GPU上不同的流处理器(stream multiprocessor, SM)并发执行.1个线程块由多个线程组成,1个流处理器可以顺序或并发地运行多个线程块.线程块内的线程具有相同的生命周期,所有的线程都可以访问GPU内部的全局内存. 在CUDA中,流(stream)[12,14]可以使主机与设备(GPU)之间的内存操作与内核操作并发执行,并且支持在GPU上的多个内核并发执行,并支持多GPU并发执行.在下面AC4GPU算法使用了CUDA流,并发地执行2个不相干的任务,将约束传播与约束网络的相容性验证并发执行,从而提升算法性能.CUDA也拥有优秀的并行模板库——Thrust[15],它采用STL的编程风格,用精简的代码实现了高性能的并行程序.本文实验程序采用Thrust库函数编写. V=v_vals(P); scp(c)={x1,x2,…,xr}∧(a1,a2,…,ar)∈ support(c)}. V=v_vals(P); scp(c)={x1,x2,…,xr}∧(a1,a2,…,ar)∈ conflict(c)}. 3.1 适用于GPU运算的约束网络模型:N-E模型 定义6中我们引入了相容超图和不相容超图的概念,它们各自记录约束网络的一部分.根据定义6,本节提出一种在GPU上表达约束网络的数据结构——N-E模型,该模型可以完整地表达约束网络,并利用GPU擅于大规模并发处理数组元素的特点,使得约束网络可以在此基础上进行并行化推理. 定义7. 点集(nodes).在约束网络P=(X,C)中,nodes表示网络中所有点组成的集合及它们在约束传播过程中的存在情况,可以形式化表示为 nodes={〈x,v,e〉|x∈X,v∈dom(x), e=(v∈dom(x)dom(x))}, 其中,e表示(x,v)在约束传播过程中是否被删除.nodes中的元素称作node,是1个三元组,即node=〈x,v,e〉. 定义8.edge元组.在标准二元约束网络P=(X,C)中,∀c∈C,有∃i,j使得xi,xj∈scp(c),∃k,l使得vk∈dom(xi),vl∈dom(xj);现定义1个五元组edge=〈xi,vk,xj,vl,s〉,其中s为2个点(xi,vk)与(xj,vl)对于c的满足情况.由此可以将edge的概念推广到标准约束网络. 在标准约束网络P=(X,C)中,∀c∈C,有∃i,…,k,使得scp(c)={xi,…,xk},∃l,…,n使得vl∈dom(xi),…,vn∈dom(xk);现定义1个元组edge=〈xi,vl,…,xk,vn,s〉,其中s为一组点(xi,vl),…,(xk,vn)对于c的满足情况. 定义9. 边集(edges).edges是P中所有edge元组组成的集合. edge∈edges∧edge.s=⊥}. xk,vn}∈edge,edge∈edges}. 故edge是边集E中对应元组扩展1个标识位s后得到的,这个标识位用来表示该元组的相容情况;node是点集中V对应元组扩展1个标识位e后得到的,这个标识位表示该点是否存在. 对于如例1所示的二元约束网络,用N-E表示的形式如表1、表2所示: Table 1 Data in nodes Table 2 Data in edges 原有的弧相容算法大多基于串行思想提出,具有一般串行算法的特点:1)算法流程中含有大量复杂的逻辑判断,具有分支多、逻辑复杂的特点;2)对附加数据结构的处理大多采用串行的方式,对于具有较大的附加数据结构的算法,往往以串行的形式构建它们时就花费了较多的时间.而GPU是细粒度的并行计算设备,在其上执行这种分支较多,具有复杂逻辑判断的串行算法非常耗时.然而GPU可以快速地以并行的形式创建大规模的附加数据结构,并对其进行并行操作,这大幅节约了算法的执行时间. N-E模型是一种对约束网络的细粒度表示方法,它将约束网络每个点的存在情况记录在nodes中,将每组值对的相容性记录在edges中.这种模型内部的元素具有相同的结构,元素之间独立性强,便于在GPU上生成并进行大规模的并行计算处理. 定理1. 对于给定的标准约束网络P,其N-E模型表示形式为N_E(P)=(edges,nodes).其中nodes的空间复杂度为O(nd);每个约束含有的相容和不相容的值对(即edge)为O(dr),则edges的空间复杂度为O(edr),对于标准二元约束网络edges的空间复杂度为O(ed2). 3.2 基于GPU生成N-E模型的并行算法:BuildNE 尽管N-E模型具有较高的复杂度,但得益于GPU在并发处理集合的能力,将约束网络P转换为N-E模型的过程较为便捷.本节我们提出生成N-E模型的算法BuildNE算法. 算法2. BuildNE算法. 输入:P=(X,C); 输出:N_E(P). ①ComputeEdgeOffset〈|C|〉 (in:P; out: ole); ②oe←Exclusive_Scan(ole); ③ComputeNodeOffset〈|X|〉 (in:P; out: oln); ④on←Exclusive_Scan(oln); ⑤BuildEdgesLaunch〈|C|〉(in:P,oe; out: edges); ⑥BuildNodesLaunch〈|X|〉(in:P,on; out: nodes). 过程1.ComputeEdgeOffset. 输入:P; 输出:ole. ①c←C[thread_id]; ②x0,x1←scp(c); ③ole[thread_id]←|dom(x0)|×|dom(x1)|. 过程2.ComputeNodeOffset. 输入:P; 输出:oln. ①x←X[thread_id]; ②oln[thread_id]←|dom(x)|. 过程3.BuildEdgesLaunch. 输入:x0,x1,c,start_index; 输出:edges. ①c←C[thread_id]; ②x0,x1←scp(c); ③start_index←oe[thread_id]; ④BuildEdges〈|dom(x0)|×|dom(x1)|〉(in: x0,x1,c,start_index; out:edges). 过程4.BuildEdges. 输入:P,on; 输出:edges. ①v0←x0[block_id]; ②v1←x1[thread_id]; ③index←start_index+thread_id+ |dom(x0)|×block_id; ④edges[index]←〈x0,v0,x1,v1,s〉. 过程5.BuildNodesLaunch. 输入:P,on; 输出:nodes. ①x←X[thread_id]; ②start_index←on[thread_id]; ③BuildNodes〈|dom(x)|〉 (in:x, start_index; out:nodes). 过程6.BuildNodes. 输入:x,start_index; 输出:nodes. ①v←x[thread_id];e←1; ②index←start_index+thread_id; ③nodes[index]←〈x,v,e〉. 伪代码函数“F〈n〉”尖括号括起来的部分表示启动多个线程执行相同的函数F,n表示启动的线程数目. 算法2的行①为每个约束启动1个线程,计算该约束含有edge元组个数存入ole数组中.行②对ole数组进行排他性扫描求oe数组,oe表示对应约束的元组1在edges数组的位置.行⑤启动过程3,以oe为参数,先启动|C|个线程,每个线程可以得到1个约束c∈C,scp(c)={x0,x1},在每个线程中再次启动|dom(x0)|×|dom(x1)|个线程执行过程4,过程4每个线程从程序运行环境取得v0和v1,从参数中取出x0和x1,并查表取得相容性情况s,填满edge的5个元组,最后按照oe经计算确定edge元组在edges数组的位置. 算法2的行③④⑥用来计算nodes,所用方式与计算edges的方式类似,这里不予赘述. 4.1 AC4GPU 算法2得到了标准二元约束网络P的N-E模型:N_E(P)=(nodes,edges),算法3在此基础上提出基于GPU执行的并行弧相容算法——AC4GPU. 算法3. AC4GPU. 输入:N_E(P); 输出:P满足AC输出真,反之输出假. loop ①counter[xi,vi,xj,s]←以edges中(x0,v0,x1)和(x1,v1,x0)为键归约edges.s; ② foreach(xi,vi)∈counters.t.counter[xi,vi,xj]=0 in parallel ③nodes[xi,vi].e←0; ④ end foreach ⑤ 同步stream0,stream1; ⑥stream0: foreachedge∈edgesin parallel ⑦ ifnodes[x,v].e=0 then ⑧edges[xi,vi].s←0 andedges[xj,vj].s←0; ⑨ end if ⑩ end foreach go to loop. 本算法出现的stream语句采用了CUDA流的技术,并发执行算法中可以并行的语句,具有相同名称的stream语句串行执行,不同名称的stream之间并行执行,同步语句同步不同的stream. 1) 若P是相容的,因为算法在最后1次循环没有删点,那么在最后1次循环计算出的domX数组的每个元素与上次记录的元素都相同,即domX=domX_pre(第1次循环的domX_pre为各变量初始论域的大小),这时算法返回true. 2) 若P是不相容的,那么此时domX数组中至少有1个元素为0,即∃x∈X,使得domX[x]=0,这时算法返回false.算法启动后,会一直循环地执行下去,直到P达到满足上述两者之一时退出,并给出P的相容性状况及用N-E表示的约束网络. 如例1所示的约束网络上执行算法3的过程如表3~14所示: Table 3 counter: Obtained from Reduce Table 2 by 3 Keys in Line ① Table 4 nodes: Modified According to Table 3 in Line ② Table 5 edges: Modified According to Table 4 in Line ⑥, Parallel with Table 6 Table 6 domX: Modified According to Table 4 in Line , Parallel with Table 5 Table 7 counter: Modified According to Table 5 in 2nd Loop Line ① Table 8 nodes: Modified According to Table 7 in 2nd Loop Line ② Table 9 edges: Modified According to Table 8 in 2nd Loop Line ⑥, Parallel with Table 10 Table 10 domX: Modified According to Table 8 in 2nd Loop Line , Parallel with Table 9 Compared with Table 6, some items have been modified. It does not meet the exit condition. The loop will continue. Table 11 counter Modified According to Table 9 in 3rd Loop Line ① Table 12 nodes: Modified According to Table 11 in 3rd Loop Line ② Table 13 edges: Modified According to Table 12 in 3rd Loop Line ⑥, Parallel with Table 14 Table 14 domX: Modified According to Table 12 in 3rd Loop Line , Parallel with Table 13 Compared with Table 10, all items indomXhave not been modified. It means the networkPis AC and the program exits. 定理2. 对于给定的标准二元约束网络P,对应的N-E模型表示为N_E(P)=(nodes,edges),在 该 模型上执行AC4GPU算法的步骤复杂度为O(ndloged2),空间复杂度为O(ed). 该算法附加数据结构为counter,domX与domX_pre,其中counter的空间复杂度O(ed),domX与domX_pre复杂度均为O(n),故整个算法的空间复杂度为O(ed). 证毕. 4.2 AC4GPU+ 从第5节实验数据我们可以看出,AC4GPU算法得益于GPU执行大规模并发算法的优秀表现,在单次弧相容算法中取得了较好的效果.但通过分析算法可以发现,每次循环都要执行的按键归约使算法性能大打折扣.以算法3行①为例,该行代码意在N-E模型上求1次counter数组,相当于原AC4算法中的初始化操作,然而AC4算法只执行1次初始化操作,相比较而言AC4GPU算法则需在每次循环时都执行1次,这大幅增加了执行时间. AC4GPU+将AC4GPU拆分成初始化和传播2个阶段,通过对N-E模型的扩展,为每个edge元组添加字段m0,m1,用来记录该edge归约到counter数组的位置,记为N_E+(P)=(nodes,edges+).算法引入一种特殊的锁机制——原子操作[16],通过m0,m1字段,直接计算counter值,从而将原算法循环最耗时的按键归约移到循环之外构成初始化阶段;传播阶段则采用循环的方式每次删掉当前中网络中所有不相容的点,该阶段求domX的按键归约改为复杂度为O(1)的原子自减操作,在网络相容性判断的主要判断分支采用O(1)的判断语句,最终使得整个传播过程中绝大多数循环的复杂度为O(1). 算法4. AC4GPU+. 输入:N_E+(P); 输出:P满足AC输出真,反之输出假. ①counter[xi,vi,xj,s]← 以(x0,v0,x1)和(x1,v1,x0)为键归约edges.s; ② 初始化domX; ③ if {ctr|ctr∈counter[xi,vi,xj]=0}≠∅ then; ④ return true; ⑤ end if ⑥ foreachcounter[xi,vi,xj]=0 in parallel ⑦nodes[xi,vi].e=0; ⑧domX[xi]←atomic_add(domX[xi],-1); ⑨ ifdomX[xi]=0 then ⑩ return false; loop parallel gotoloop. 算法4的初始化阶段与算法3的第1次循环相似,对edges按键归约求counter,修改node的e值,并且验证整个网络相容性. Fig. 3 A special-case of delete node图3 删点的特殊情况 图3中的特殊情况是scp(ci j)={xi,xj},scp(cj k)={xj,xk},vi=dom(xi),vj∈dom(xj),vk=dom(xk),现在删除(xi,vi)和(xk,vk)2个点,且这2个点是(xj,vj)分别在ci j与cj k的最后支持,此时counter[xj,vj,xi]=0且counter[xj,vj,xk]=0,在用原子操作计算domX(xj)会自减2次,这意味着(xj,vj)被删除了2次,与实际情况不相符,说明在算法执行的过程中domX的值可能是不对的.由于nodes保存的每个点存在的信息是正确的,这时需要对nodes进行1次按键归约,重新修改domX数组的值,如果这个时候发现domX[xi]仍然为0,则表示没有出现如上这类特殊情况,变量xi的论域确实已被删空,网络不相容循环退出.需要注意的是上述这类情况,同样适用于同时删除多个点的情况. 使用这种验证方式是因为在传播过程的每次循环中,出现这类特殊的删点情况且将论域删空的情况并不多见,所以只需要在出现论域删空的情况下,再次以复杂度较高的方式验证,而其他时间,则以O(1)的方式进行验证,这样达到了节省时间的目的. 同AC4算法相比, AC4GPU+算法初始化阶段求counter的过程是通过对edges数组按键归约完成的;整个edges数组由于记录了约束网络的关系,可以看作是AC4算法中的S数组;nodes数组则可以看成是AC4算法的待删除点的队列Q. 同AC4GPU算法相比,AC4GPU+算法将原算法单一的循环,拆分成初始化和传播2个阶段,整个算法仅在初始化时执行1次最为耗时的按键归约操作,在传播阶段每次循环都删除所有不相容的点,而在该阶段对网络的相容性验证,绝大多数情况采用复杂度为O(1)的判断分支,仅在出现变量值域删空的情况下,采用步骤复杂度较高的分支,验证是否产生特殊情况. 定理3. 对于给定的标准二元约束网络P,对应的N-E模型表示为N_E(P)=(nodes,edges),在 该 模型上执行AC4GPU+算法的步骤复杂度为O(ndlognd)、空间复杂度为O(ed). 综上,2个阶段步骤复杂度的和为O(loged2+ndlognd),在标准二元约束网络中n≥2,d≥1,1≤e≤n2,即loged2≤logn2d2=2×lognd≤nd×lognd,即loged2≤nd×lognd,则理论上整个算法的步骤复杂度为O(ndlognd),该算法较之AC4GPU在理论上有显著提升. 算法4附加数据结构为counter,domX,如4.1节所证,counter的空间复杂度O(ed),domX空间复杂度为O(n),故整个算法的空间复杂度为O(ed). 证毕. 需要注意的是:我们理论上按照最坏的情况计算了算法复杂度,通过比较忽略了初始化部分的步骤复杂度,但并不表示在所有测试用例中初始化的时间都可以忽略.这里ndlognd的系数nd指的是删除点所用的循环次数,循环次数的取值范围是[0,nd],若传播阶段没有需要被删除的点,则该阶段耗费时间为0.所以本算法在具体测试用例的执行中,若循环次数小于特定值,则可能出现初始化阶段所耗费的时间大于传播阶段,这与循环次数以及循环内部执行的具体的判断分支有关,因问题而异,这里不能给出准确阈值. 5.1 实验程序设计 由于AC4GPU和AC4GPU+是基于AC4的并行化改进,我们将3个算法进行对比实验,为了获得实验流程各个细节的数据,设计了如下的实验程序: 如图4所示,对比程序将benchmark文件读入内存;再将数据存入显存中;分别在CPU中建立约束网络,在GPU中建立N-E模型;最后分别在CPU执行串行的AC4算法,在GPU中执行并行的AC4GPU和AC4GPU+算法.实验数据记录各模块的执行时间,下面会对这些数据进行分析. 本文采用目前国际通用的测试约束满足问题的标准库用例,所有测试文件可以从文献[17]在线下载. 实验环境:CPU为Intel Core i5-4590 3.33 GHz, 4 GB RAM;GPU为NVIDIA GTX750[18],512个CUDA核心,GPU Clock 1215 MHz,1 GB RAM. Fig. 4 The experimental process design图4 实验流程设计 5.2 N-E模型测试实验 为了测试各用例在建立N-E模型的情况,表15给出了常见测试用例的文件大小、传输时间、建模时间、edge个数、node个数. Table 15 Size and Build Model Time of Benchmarks 从实验数据可以看出,测试用例在内存到显存的传输时间不可忽略,主要由于现有编程模型对GPU的限制,GPU不能直接从文件中读取数据到显存,必须通过 CPU先将数据读入内存,再将数据从内存复制到显存中,内存的吞吐量远不及核心计算的吞吐量,受限于多核系统的结构,内存数据传输延迟成为了制约并行算法加速的一大难题[19].与之相比,建模时间较短且与测试用例的问题规模有关,即与N-E模型的大小有关,然而如果接下来继续在GPU上执行弧相容算法或求解算法,则数据拷贝仅此1次且是单向的,此后数据结构被维持在显存中. 在GPU中对约束网络进行N-E建模后,GPU中执行并行弧相容算法AC4GPU和AC4GPU+,它们与AC4算法执行时间的比较如表16、表17所示. Table 16 Experimental Comparison of Composed Problems Composed问题(表16中简写为cpd)是一组具有特殊结构的问题,由于许多实例在执行第1次弧相容时就需要删点,这里用来测试并行弧相容算法,表16中给出了部分Composed用例的算法性能对比情况,其中循环次数是指在执行算法3、算法4循环的次数;每次循环中删去点的个数用“”隔开,例如611表示在算法3第1次循环(对应算法4初始化阶段)删去6个点,而后每次循环删去1个点.从实验数据可以看出,AC4算法的执行时间随问题规模的增大而增大,主要原因是由于初始化占用了大量时间.而AC4GPU和AC4GPU+的执行时间与问题规模的关系不明显,却与循环次数有关. 通过cpd-25-1-25-1 和cpd-75-1-2-4执行时间进行对比我们可以看出,其AC4GPU算法的执行时间与用例本身的迭代次数成正比,即执行算法的循环迭代的越多,耗费的时间越多,AC4GPU每次增加一次迭代大约增加1ms的执行时间;AC4GPU+对循环进行了改进,执行时间明显减少.在删除节点较多的情况下,由于AC4GPU和AC4GPU+算法是在每次循环中并行删除多个点,而AC4算法则是在每次循环删除1个点,但由于并行算法的内存读取速度限制,其性能有否提升还有待研究. 表17给出了3个算法在一些随机问题上的性能比较,由于这些问题在执行弧相容算法时不删除点,所以循环次数为1.由实验数据可以看出,串行算法执行时间随问题规模的增大而增大;并行算法的执行时间取决于GPU的并行度.若测试用例的问题规模测大于GPU可启动的线程数,GPU需要分多次启动线程进行计算,由此可知,对于那些GPU启动相同次数进行处理的测试用例,它们的执行时间相近,故并行算法的执行时间随启动次数增加而增加. Table 17 The Experimental Comparison of Random Problem 本实验采用的GPU为GTX750,该GPU具有4个流多处理器(SM),每个SM上有128个流处理器(SP),共有512个CUDA核心(SP),每个SM最多可以启动2 048个线程,总共可以启动8 192个线程,如果输入数组长度过大,则会将原数组分割成多个部分进行计算.由于edge具有对称性,即〈x0,v0,x1,v1,s〉等价于〈x1,v1,x0,v0,s〉,本实验程序采用BuildNE建立1个edge时同时生成了2个元组,即对于问题tightness0.8,实际上其edges拥有1 318 400个元素,底层归约算法将原数组分割成了多个部分计算,故并行算法的执行时间相对较长.同理,对于问题tightness0.9,底层算法将其分割为更多部分进行计算,所以耗时更长. 综上,并行弧相容算法用并行的手段节约了AC4在初始化阶段的巨大花费,并在每次循环中并行地删除所有不相容的点,最终经实验结果证明,该算法较AC4算法有所提高. 针对基于GPU的并行计算在解决某些问题的优点,本文对结合并行计算的基本算法对弧相容问题进行了研究,提出了一种便于GPU并行计算约束网络的表示模型——N-E模型;给出了在GPU中生成该模型的算法——BuildNE;并将经典的AC4算法结合并行计算的基本思想,提出一种细粒度的并行弧相容算法——AC4GPU及其改进AC4GPU+.进而通过实验给出了常见测试用例以N-E模型表示的大小与的创建时间,分析并行弧相容算法较于传统弧相容算法的特点和优势. 利用算法并行删除多个点的优点,对于一些需要快速删点的求解问题,并行算法一定会发挥很大作用.未来的工作是在此基础上对并行化约束满足问题进行进一步的研究,包括对并行化分支搜索、单弧相容算法、约束求解算法等基于弧相容算法的高级算法进行并行化的扩展;利用N-E数组元素间的相对独立性,研究该模型在约束划分、辨别特殊的约束网络的模式上的可能应用. [1]Freuder E C, Mackworth A K. Constraint Satisfaction: An Emerging Paradigm[M]. Amsterdam: Elsevier, 2006: 13-27 [2]Bessière C. Constraint Propagation[M]. Amsterdam: Elsevier, 2006: 29-84 [3]Mohr R, Henderson T C. Arc and path consistency revisited[J]. Artificial Intelligence, 1986, 28(2): 225-233 [4]Lecoutre C. Generic GAC Algorithms[M]. London: ISTE Ltd, 2009:185-236 [5]Nguyen T, Deville Y. A distributed arc-consistency algorithm[J]. Science of Computer Programming, 1970, 30(12): 227-250 [6]Yokoo M, Durfee E H, Ishida T, et al. The distributed constraint satisfaction problem: Formalization and algorithms[J]. IEEE Trans on Knowledge & Data Engineering, 1998, 10(5): 673-685 [7]Ringwelski G. An arc-consistency algorithm for dynamic and distributed constraint satisfaction problems[J]. Artificial Intelligence Review, 2005, 24(34): 431-454 [8]Campeotto F, Palù A D, Dovier A, et al. Exploring the use of GPUs in constraint solving[C]Practical Aspects of Declarative Languages. Berlin: Springer, 2014: 152-167 [9]Gent I P, Jefferson C, Miguel I, et al. A preliminary review of literature on parallel constraint solving[C]Proc of PMCS 2011 Workshop on Parallel Methods for Constraint Solving. Berlin: Springer, 2011: 499-504 [10]Christophe L. Constraint Networks[M]. London: ISTE Ltd, 2009: 39-92 [11]Wilt N. Reduction[G]CUDA Handbook: A Compr-ehensive Guide to GPU Programming. Reading, MA: Addison-Wesley, 2013: 365-384 [12]NVIDIA. CUDA C Programming Guide, version 7.0[OL]. [2015-06-25]. https:developer.nvidia.comcuda-zone [13]Wilt N. Scan[G]CUDA Handbook: A Comprehensive Guide to GPU Programming. Reading, MA: Addison-Wesley, 2013: 173-204 [14]Nicholas W. Stream and event[G]CUDA Handbook: A Comprehensive Guide to GPU Programming. Reading, MA: Addison-Wesley, 2013: 385-420 [15]NVIDIA. Thrust Quick Start Guide. version 7.0[OL]. [2015-06-25]. http:docs.nvidia.comcudapdfThrust_Quick_Start_Guide.pdf [16]Butcher P. Seven Concurrency Models in Seven Weeks: When Threads Unravel[M]. Raleigh, NC: Pragmatic Bookshelf, 2014 [17]Lecoutre C. Benchmarks of constraint satisfaction problem[OL]. [2012-04-16]. http:www.cril.univ-artois.fr~lecoutrebenchmarks.html [18]NVIDIA. Geforce GTX 750 specifications[OL]. [2015-06-25]. http:www.geforce.cnhardwaredesktop-gpusgeforce-gtx-750 [19]Sun Xianhe, Chen Yong. Reevaluating Amdahl’s law in the multicore era[J]. Journal of Parallel & Distributed Computing, 2010, 70(2): 183-188 Li Zhe, born in 1990. MSc. His main research interest is constraint programming (leezear@live.cn). Li Zhanshan, born in 1966. PhD, professor of Jilin University. Member of CCF. His main research interests include constraint solving, model-based diagnosis, intelligent planning and scheduling. Li Ying, born in 1965. PhD, professor, PhD supervisor. Her main research interests include large data processing, geological 3D visualization modeling, 3D geological image processing, geological model data processing, etc (l_ying@jlu.edu.cn). A Constraint Network Model and Parallel Arc Consistency Algorithms Based on GPU Li Zhe, Li Zhanshan, and Li Ying (CollegeofComputerScienceandTechnology,JilinUniversity,Changchun130012) (KeyLaboratoryofSymbolicComputationandKnowledgeEngineering(JilinUniversity),MinistryofEducation,Changchun130012) Constraint satisfaction problem is a popular paradigm to deal with combinatorial problems in artificial intelligence. Arc consistency (AC) is one of basic solution compression algorithms of constraint satisfaction problem, which is also a core algorithm of many excellent advanced algorithms. When constraints are considered independently, AC corresponds to the strongest form of local reasoning. An effective underlying AC can improve the efficiency of reducing the search space. Recent years, GPU has been used for constituting many super computers, which solve many problems in parallel. Based on GPU’s computation, this paper proposes a constraint networks presentation model N-E and its parallel generation algorithm BuildNE. According to fine-grained arc consistency AC4, a parallel edition AC4GPUand its improved algorithm—AC4GPU+, are proposed. The two parallel algorithms extend arc consistency to GPU. Experimental results verify the feasibility of these new algorithms. Compared with AC4, the parallel versions have made the 10% to 50% acceleration in some smaller instances, and obtained 1 to 2 orders of magnitude in some bigger instances. They provide a core algorithm to other constraint satisfaction problem solving in parallel for further study. artificial intelligence; constraint satisfaction problem (CSP); arc consistency (AC); GPU; compute unified device architecture (CUDA) 2015-10-13; 2016-08-08 国家自然科学基金项目(61272208,61373052);吉林省自然科学基金项目(20140101200JC) This work was supported by the National Natural Science Foundation of China (61272208, 61373052) and the Natural Science Foundation of Jilin Province of China (20140101200JC). 李占山(zslizsli@163.com) TP18





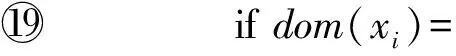






2 基本并行算法及CUDA编程技术


3 并行算法的约束网络模型

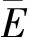









4 并行弧相容算法


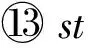










































5 实验数据



6 结论与展望



