基于保留分类信息的多任务特征学习算法

王 珺 卫金茂 张 璐

(南开大学计算机与控制工程学院 天津 300071) (南开大学软件学院 天津 300071) (weijm@nankai.edu.cn)

基于保留分类信息的多任务特征学习算法

王 珺 卫金茂 张 璐

(南开大学计算机与控制工程学院 天津 300071) (南开大学软件学院 天津 300071) (weijm@nankai.edu.cn)

在模式识别中，特征选择是一种非常有效的降维技术.特征评价标准在特征选择过程中被用于度量特征的重要性，但目前已有的标准存在着只考虑类之间的分离性而未考虑其相关性、无法去除特征之间的分类冗余性以及多用于单变量度量而无法获取子集整体最优性等问题.提出一种保留分类信息的特征评价准则(classification information preserving, CIP)，并使用多任务学习技术进行实现.CIP是一种特征子集度量方法，通过F范数实现已选特征子集的分类信息与原始数据分类信息的差异最小化，并通过l2,1范数约束选择特征个数.近似交替方向法被用于求解CIP的最优解.理论分析与实验结果表明：CIP选择的最优特征子集不仅最大程度上保留了原始数据类别之间的相关性信息，而且有效地降低了特征之间的分类冗余性.

特征选择；多任务学习；分类信息保留；特征冗余；近似交替方向法

特征选择是一种非常有效的降维方法，其旨在从原始数据中选择一组具有较高区分能力的特征组成特征子集[1]，从而达到降低维度以及提高精度的目的[2].特征评价准则在特征选择过程中必不可少，被准则评价为优秀的特征会被加入到特征子集中而成为降维空间的一个维度，而非优的特征会被淘汰.

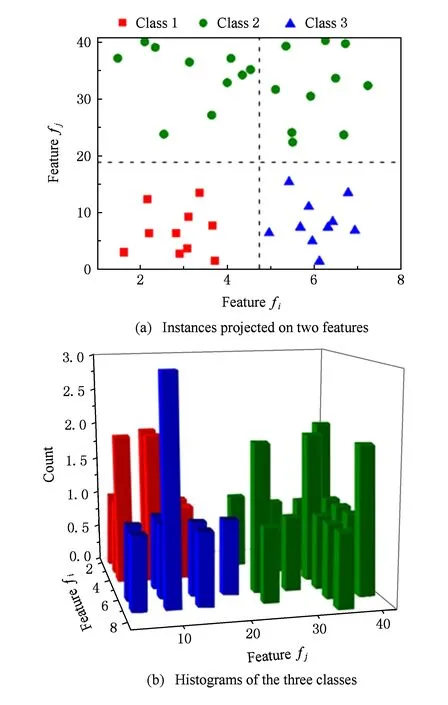
Fig. 1 Distributions of 2-dimensional instances belonging to three classes图1 3类样本在2维空间的分布图

目前常见的特征评价准则在通常情况下多用于单变量度量，其缺点在于无法保证选出的特征子集的最优性.首先，对某些类别具有高辨识度的特征不能被选出.如图1(a)所示，特征fi能较好地分离类别1和类别3，却不能辨识属于类别2的样本.同样，特征fj能较好地辨识类别2，但无法辨识类别1和类别3.所以在使用单变量评价准则的特征选择中，fi与fj会由于不能有效识别所有类而被赋予较低的权重，从而被淘汰.然而，在由2个特征组成的子空间中，所有样本均可以被正确识别，如图1(b)中直方图所示.这归因于fi与fj对不同的类别具有互补的识别性能，而这种互补性在单变量度量中往往被忽视.其次，特征之间的高度冗余性也是造成单变量度量标准选出的特征子集往往比预期性能要差的原因.冗余特征意味着其所包含的分类信息已包含于其他已选择的特征中，无法提供新的有价值的分类信息[3].而单变量度量往往无法排除掉这类特征.

Fig. 2 Correlation of two features for recognizing the target class图2 2个特征识别目标类别时的相关性

针对单变量准则的以上问题，特征子集选择法受到越来越多的关注，代表性的有SPFS(similarity preserving feature selection)[4]等.SPFS不仅被证明是诸多单变量准则[5-10]的更一般形式，而且能有效降低特征冗余性.然而，SPFS也有2点缺陷：

1) 其降低的特征冗余性并非特征之间用于识别目标类别的冗余信息，如图2所示.图2中，阴影部分为特征fi与fj分别提供的独立的分类信息，网格(红色)部分为2个特征共享的分类信息，即2个特征之间的分类冗余信息，而黑色部分为与分类无关的冗余信息.SPFS度量的是黑体部分与红点部分之和，显然是不合理的.只有降低特征之间与分类有关的冗余性，才能有效提高所选特征子集的识别性能.

2) 以SPFS为代表的保留样本相似性的方法通常以在降维空间最大化类间离散度为目标，但却忽视了类间的相关性信息.这一点在多标记数据的降维问题[11]中尤为明显.多标记分类中，一个样本通常属于多个分类，所以类与类之间具有较强的相关性[12-14].仅仅度量类间离散度、而忽略类间相关性的特征选择方法，显然是不够合理的.

针对以上问题，本文提出一种保留分类信息的特征选择算法CIP(classification information preserving)，并通过多任务学习技术进行了实现.对比其他特征选择算法，CIP具有3点优势：

1) CIP是一种特征子集选择方法，可以解决采用单变量度量无法保证子集最优性的问题；

2) CIP可以有效地降低特征间的分类冗余性，从而提高特征子集的分类识别性能；

3) CIP可以在降维空间最大程度上保留原空间类别间的相关性信息，从而对多标记数据有较好的分类效果.

1 保留样本相似性的特征选择法

近年来，基于保留样本相似性的特征选择法应用较为普遍.不仅诸多传统的特征评价准则可以被涵盖其中，如希尔伯特-施密特独立性准则(Hilbert-Schmidt independence criterion，HSIC)[5]、拉普拉斯得分(Laplacian Score)[6]、费舍尔得分(Fisher Score)[7]、微量比准则(trace ratio)[8]及ReliefF[9]等，且基于其核心思想，一些新方法也被不断提了出来，如谱特征选择(spectral feature selection，SPEC)[10]、样本相似性保留特征选择SPFS[4]等.

HSIC通过核函数来度量特征与类别之间的依赖性，以选出对类别依赖性最大的特征子集.Laplacian Score是一种基于拉普拉斯特征映射和局部保留投影的度量方法，局部保留能力强的特征会被选入到最优特征子集中.Fisher Score通过度量类内紧凑度与类间离散度[15]来判定特征的识别性能，优秀的特征可以保证在降维空间中同类样本之间的距离较小、而不同类样本之间的距离较大.同样的想法也被用于ReliefF中.不同的是，ReliefF统计的是随机抽取的样本与其在同类及不同类中的若干最近邻样本之间的差异性.基于谱图理论，SPEC试图在降维空间中最大程度上保留原空间的谱信息，来获取对各分类较高的辨识度.该方法不仅可用于有监督的特征选择，而且同样适用于无监督的特征选择[16].在文献[4]中，一种更具普适性的样本相似性保留算法SPFS被提出，该方法被归结为HSIC，Laplacian Score，Fisher Score，trace ratio，ReliefF，SPEC的一般形式.

以上方法是比较流行且有效的特征选择方法，但仍存在无法度量特征间分类冗余性、无法在降维空间保留类别间的相关性信息以及多数方法只能用于单变量度量等问题.而本文提出的CIP方法可以较好地解决这些问题.

2 保留分类信息的特征选择法CIP

F=(fj)∈n×m描述，响应yi∈c由类标记C=(cl)∈描述.则保留分类信息的特征子集评价准则CIP定义如下：

(1)

其中,S为c个类的相似度矩阵，k为选择特征的个数.

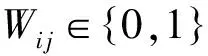
其中，j=1,2,…,m.

对于式(1)有:

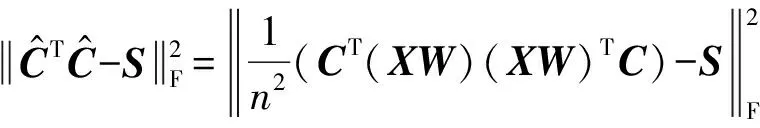
命题1. CIP可以最小化特征间的分类冗余性.

证明.

)，

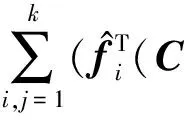
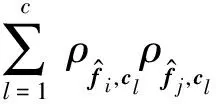
证毕.

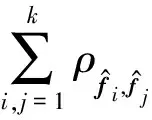
命题2. CIP可以最大化保留原空间的类间相关性信息.

证明.

tr(STH)=((XW)TCSCT(XW))=

其中，sl1,l2代表类cl1与cl2之间的相似度.由此可得：

证毕.

3 CIP的稀疏多任务学习实现

式(1)中的CIP准则是一个整数规划问题.因此它是NP难问题，直接求解比较复杂.此外，式中的l2,0范数约束也是非平滑的，这意味着式(1)的收敛速度通常会比较慢[17].鉴于以上2方面原因，本节将重新规划CIP的求解形式，进而使用稀疏多任务学习技术对其进行实现.

3.1 CIP的多任务学习规划

将相似性矩阵S进行谱分解，可得：

(2)

其中，σ1≥σ2≥…≥σc，Φ和Σ分别为S的特征向量与特征值矩阵.则式(1)可以表示为

(3)

其中，p是指示变量，反映了对应的特征是否被选中.显然这是一个多变量回归问题，可以通过多任务学习技术来解决[18-19].按照这个思路，将式(3)进一步表示为

(4)

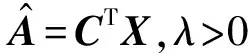
将使用拉格朗日增量法求解式(4)中的多变量最小化问题.式(4)的等价形式可表示为

(5)

则定义拉格朗日函数如下：

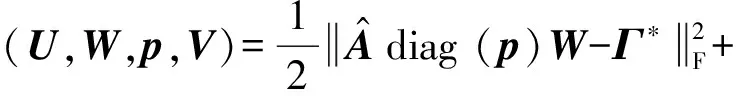
(6)

对L1(U)而言，有等式成立：

(7)

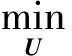
(8)

通过梯度下降法求解式(8)，可得其最优解为

(9)

同理U在[t+1]次迭代的最优解可表示为

(10)

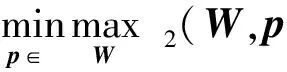
(11)

先固定变量p，则可得W的最优解为

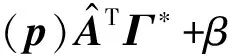
(12)

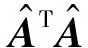
(13)

其中，τ>0，W[t]为W在第[t]次迭代得到的最优解.则W在第[t+1]次的最优解为

(14)

同理，p的最优解也可以通过固定W得到.此时式(11)等价于以下的最小化问题：

(15)

值得注意的是，矩阵V为了问题简化而在上述求解过程中取值被暂时固定.现采用近似交替方向法(proximal alternating direction method， PADM)[20]来实现以上求解，则可知在此框架下，V在[t+1]次迭代的最优解可表示为

(16)

3.2 CIP的算法设计

算法1将使用PADM来实现3.1节的推导.PADM是一种有效的解决多变量回归问题的规划方法.在文献[20]中已证明，对∀β>0，PADM可以从任何初始点{W[0],U[0]}开始迭代，而最终收敛于式(5)的最优解{W*,U*}.

算法1. 保留分类信息的特征选择法(CIP).

输入：F=(f1,f2,…,fm),C,S,k,β,τ,λ；

输出：p[t].

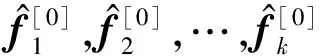
③ while “未满足收敛条件”

④ 根据式(10)计算U[t+1]；

⑤ 根据式(14)计算W[t+1]；

⑦ 根据式(16)更新V[t+1]；

⑧t=t+1；

⑨ end while；

⑩ returnp[t].

就时间复杂度而言，算法1中从m个候选特征里排序选出最优的k个特征的时间复杂度为O(klogm).因此，CIP总的时间复杂度为O(t(m2c2+nmc2+klogm)).

4 实验结果

本节将CIP方法与7种比较流行的特征选择方法进行比较，这些方法包括SPEC，SPFS，ReliefF，mRMR(minimal redundancy maximal relevance)[21]，Laplacian Score，Fisher Score，MSMTFL(multi-stage multi-task feature learning)[19].其中，SPEC，SPFS，ReliefF，Laplacian Score，Fisher Score可视为保留样本相似性的方法，且除SPFS之外其他方法均为单变量度量，而SPFS为特征子集度量.mRMR是一种基于互信息[22]的特征选择方法，不仅算法本身的性能比较高，而且被证明可以有效的降低特征之间的冗余性，所以也将其与CIP进行比较.MSMTFL是一种多任务学习方法，它通过截断l1,l1范数来求解非凸优化问题，从而实现多任务稀疏特征选择.

4.1 实验设置

对于CIP而言，其类间相似度矩阵S定义为

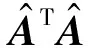
值得注意的是，算法1中涉及到CIP选择过程的收敛条件，这里采用2种收敛条件，只要满足其一即可判定为收敛：

1) 最大迭代次数tmax=103；

4.2 人工数据

在spider①环境下随机生成2组带有噪声特征的测试数据，以测试对比算法对噪声特征的处理性能.在2组数据中，只有前5个特征与目标类别高度相关，剩余特征均为与分类无关的高斯噪声特征.在第1组数据中，特征数m固定为50，样本数n从30逐渐增加到300，间隔为30.在第2组数据中，样本数n固定为300，特征数m从30逐渐增加到300.

各对比算法按照各自特征评价准则对数据中的所有特征进行排序，实验结果记录下前5个高度相关特征在各个排序结果中的平均位置.位置越靠前、即所得结果值越小.说明算法对噪声特征具有越好的抗噪能力.实验结果如图3所示.

由图3可以看出，无论是样本数量改变还是候选特征数量改变，CIP选择最优特征的能力都是比较出色的.在图3(a)中，当样本数量较少时，各方法从噪声特征中选出有用特征是比较困难的，这种情况下CIP的性能要明显优于其他算法.随着样本数量增加，各算法选择特征的能力也逐渐增强，此时CIP的表现比较优秀而且稳定.在图3(b)中，随着候选特征数量的增加，CIP与mRMR，Laplacian Score，Fisher Score表现均比较稳定，而SPFS的波动比较明显，说明SPFS对噪声特征的处理能力要弱于其他算法.这主要是由于SPFS从本质上来讲是一种去冗余的特征选择方法，在本实验中其采用了前向的贪心搜索策略，所以在对候选特征进行评价选择时，SPFS会优先选择低冗余特征而非具有较强分类能力的特征，因此在本实验中其性能要弱于其他对比方法.

Fig. 3 Average ranks of the correlated features with the increase of instance number and feature number图3 相关特征随着样本数和特征数增加的平均排序位置

4.3 单标记数据

本节与4.4节将测试各算法在真实数据上的特征选择性能.14组单标记数据在本节被用来进行测试，如表1所示:

Table 1 Test Data of Single-Label Task

表1中既有低维度数据，也有高维度数据.类别数目从2～16不等，所以以下的实验中同时包含了2分类问题及多分类问题.数据来源包括UCI数据①、微阵列数据(microarray)[4,10,23]以及脸部识别数据(face recognition)[4,6,10].各对比算法依次选取1,2,…,50个最优特征组成特征子集，即特征数k从1依次增加到50.Ionosphere数据集和Tennis Major Tournaments数据集的特征数m<50，所以这2个数据集的k值最多增加到m.

4.3.1 分类精度

在weka②环境下被选择出的特征子集的识别性能分别通过SMO(sequential minimal optimization)分类器、朴素贝叶斯(Naïve Bayesian，NB)分类器及K-近邻(K-nearest neighbor，K-NN)分类器进行测试.其中，SMO分类器是对经典支持向量机(support vector machine， SVM)的一种实现算法，具有高效、易实现、适用于大规模数据学习等优点.NB分类器假设特征之间彼此独立，通过估计样例在类条件下的后验概率来判断其类别.K-NN分类器是一种基于距离度量的学习算法，其通过考虑每个样例K个最近邻的分类情况来判断该样例所属的类别.

各分类器分别进行10重的10折交叉验证测试，最高分类精度如表2～4所示.每行最优结果用粗体标出，最后一行统计了各算法在所有测试数据集上的平均分类精度.

由表2～4可以看出，CIP算法的性能总体上要优于被测试的其他特征选择算法.值得注意的是:通常情况下在多任务学习中，正则参数λ与惩罚参数β需要根据测试数据集的不同进行相应的调节，最常用的方法是交叉验证法.在本实验中，为了提高CIP的运行效率，而对所有测试数据集固定使用统一的参数设定.如果进行调参操作，CIP的性能通常比表2～4中的结果还会有所提高.

Table 2 Maximal SMO Classification Precision for Selected Feature Subset via Each Method

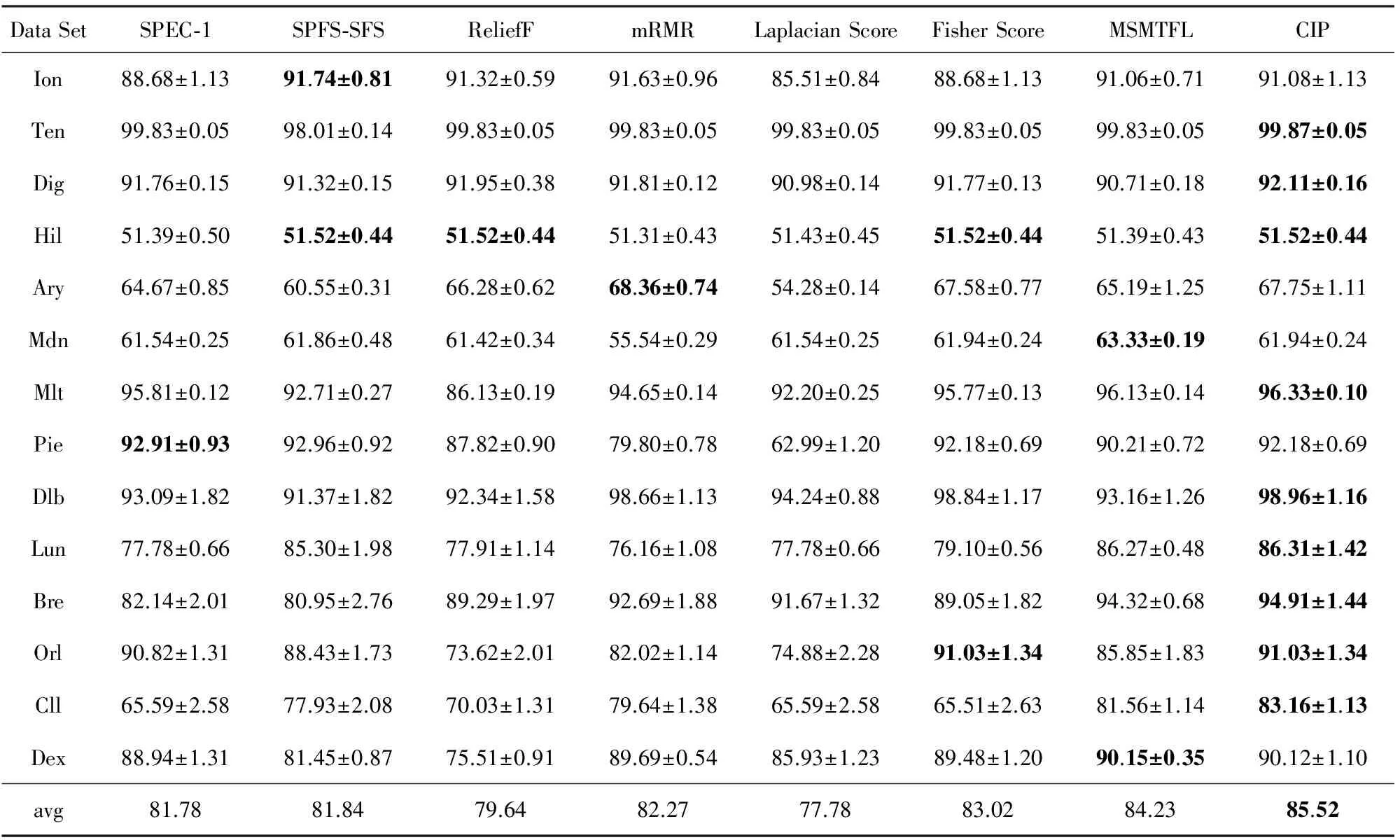
Table 3 Maximal Naïve Bayesian Classification Precision for Selected Feature Subset via Each Method

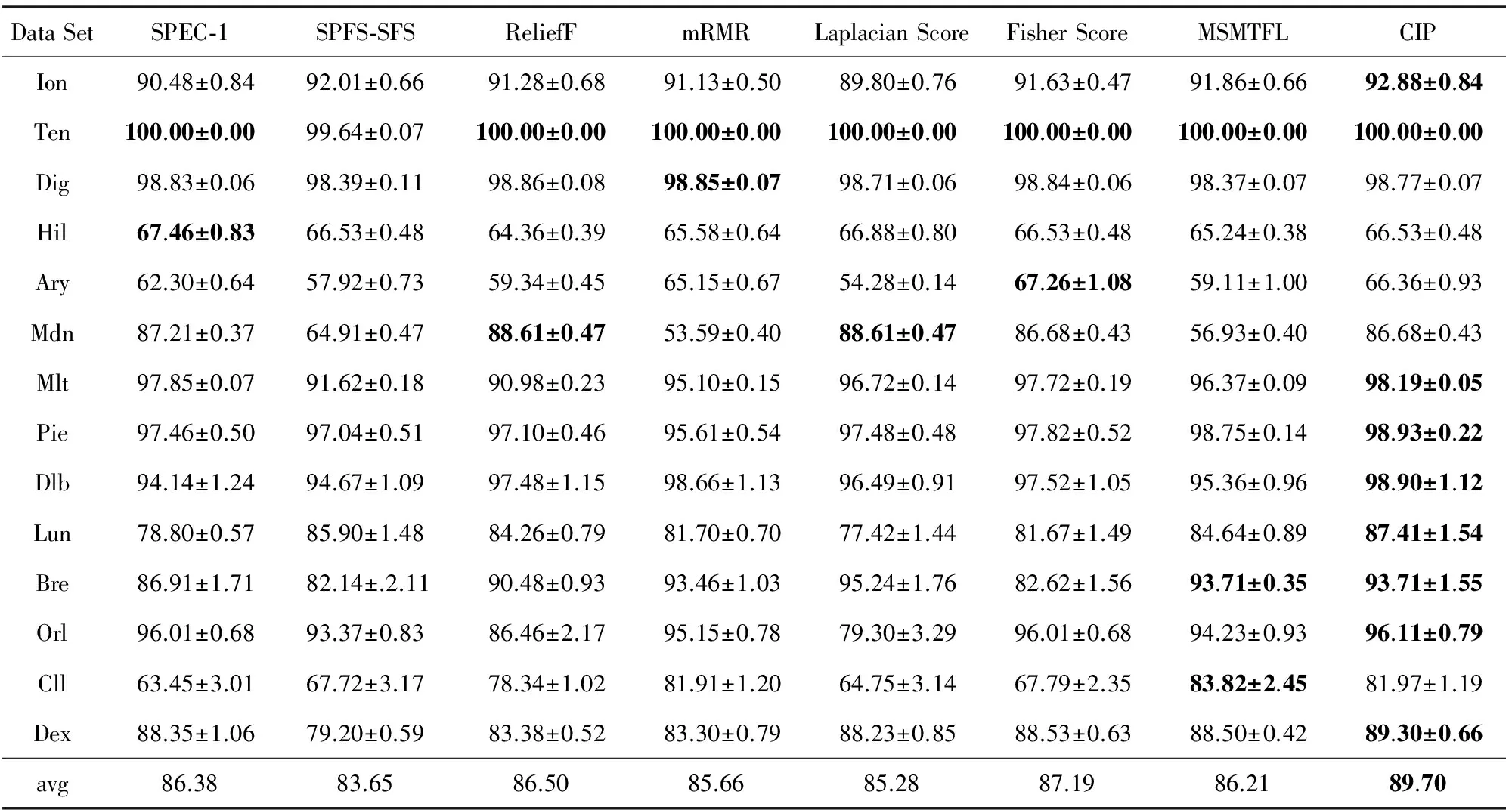
Table 4 Maximal K-Nearest Neighbor (K=3) Classification Precision for Selected Feature Subset via Each Method

4.3.2 分类冗余性

分类冗余性是衡量特征子集是否优秀的一个重要标准.冗余性越小，子集中各特征之间共享的分类信息越少，从而子集整体上提供的有效的分类信息也就越多.定义特征子集的分类冗余性如式(17)所示：

(17)

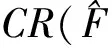
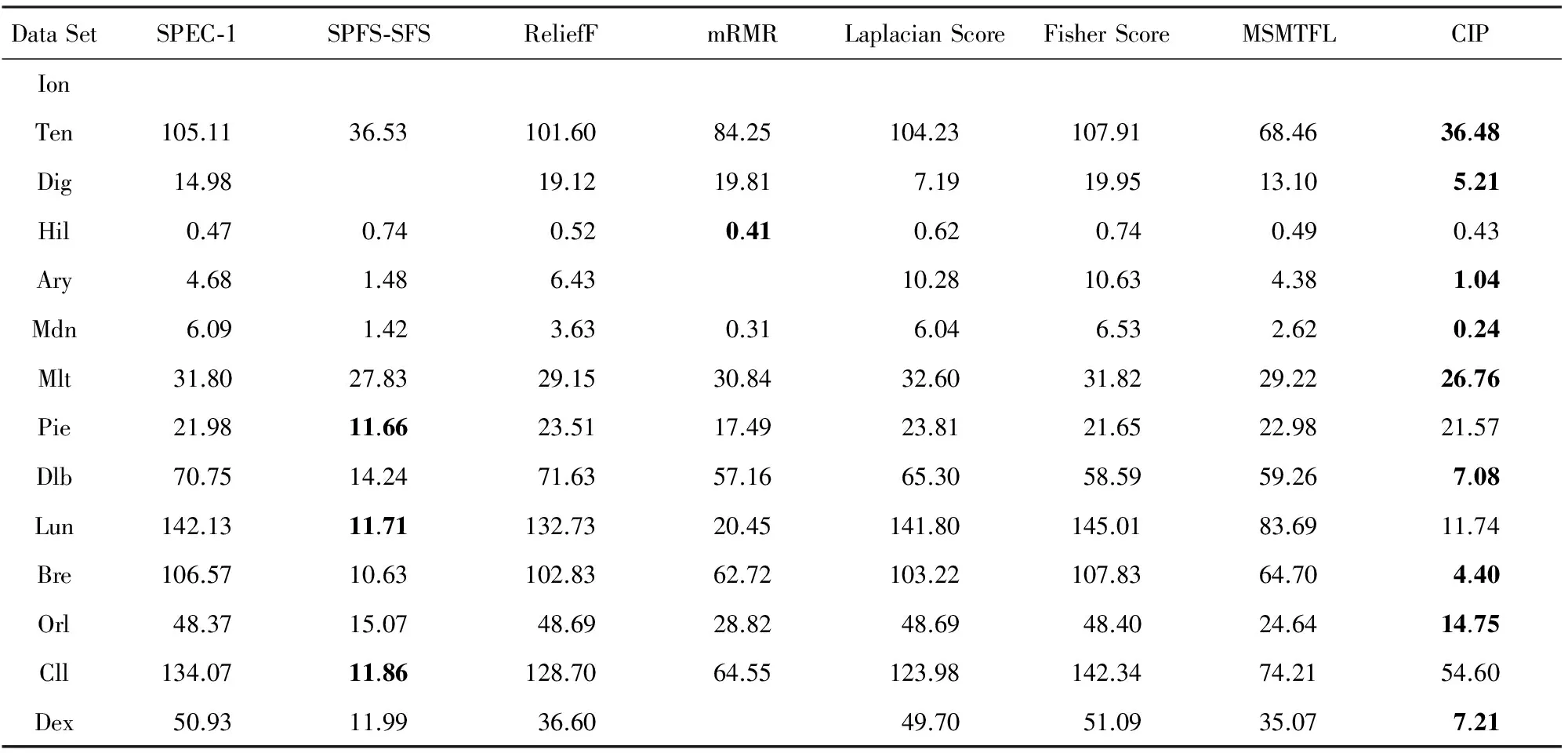
Table 5 Average Classification Redundancy for Selected Feature Subset via Each Method

4.4 多标记数据

多标记数据与单标记数据每条样本属于且仅属于一个类别不同，其部分或者全部样本具有1个以上的类别标记.也就是说，类别之间是具有关联性的.本节将测试CIP，SPEC-1，SPFS-SFS在多标记数据上的特征选择性能，以及在降维空间保留原空间类别之间相关性的能力.

从Mulanlibrary①下载6组多标记数据进行测试，如表6所示.表6中除了记录有每组测试数据集的特征数m、样本数n以及类别数c，还记录了类标签集合的势LC，即每条样本所属类别的平均数量.

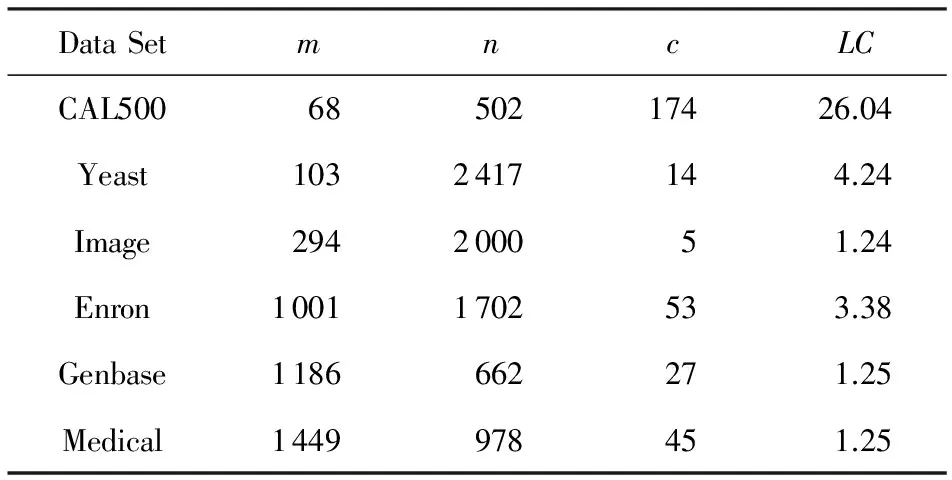
Table 6 Test Data of Multi-Label Task

4.4.1 分类精度和汉明损失

在meka②环境下对各对比算法选择出的特征子集的分类性能进行测试.分类器使用BR(binary relevance)，基础分类器采用SMO.对特征子集进行10折交叉验证分类测试，平均分类精度及平均汉明损失如表7和表8所示.

Table 7 Average BR+SMO Classification Precision for Selected Feature Subset via Each Method

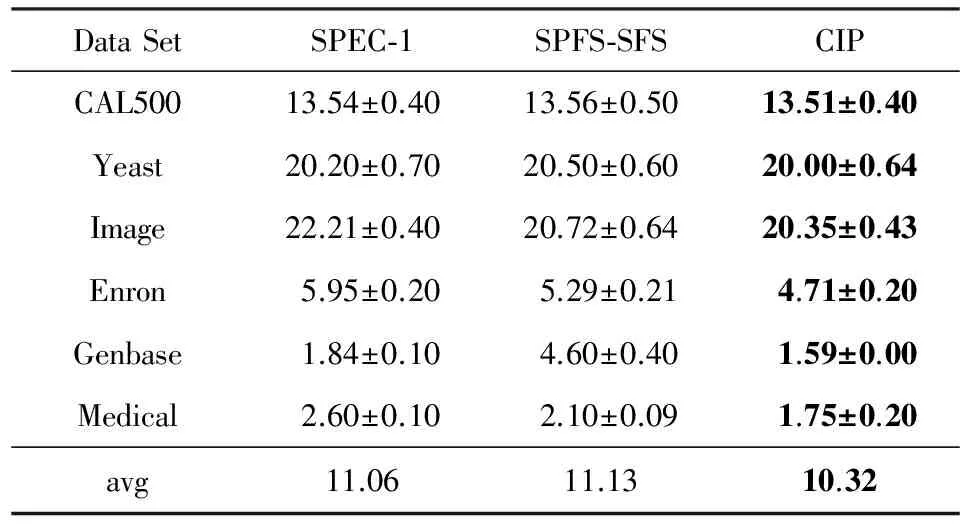
Table 8 Average BR+SMO Hamming Loss for Selected Feature Subset via Each Method

分类精度用于衡量样本是否能被正确分到其所属的所有类别中，而汉明损失则用于衡量样本是否被错误地分到某一个类别中.由表7和表8可以看出，对于这2个度量指标CIP的表现均优于SPEC和SPFS方法.后2种方法只关注类间分离性，而无法度量及保证类间相关性.CIP旨在在降维空间最大程度上保留原空间中的类间相关性信息，因此比SPEC和SPFS更适合在多标记数据中进行特征选择.

4.4.2 类间相关性

度量与保留类间相关性信息是多标记特征选择算法所要面临的主要问题之一.有效地保留这些信息有助于识别分类样本、提高算法性能.在以下的实验中，通过式(18)来计算特征子集所保留的类间相关性信息与原空间相关性信息之间的差别：

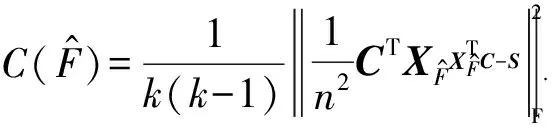
(18)

度量结果如表9所示，每行中最小的残差取值被用粗体标出.从表9可以看出，CIP具有优于SPEC和SPFS的保留类间相关性信息的能力,仅次于CIP表现的是SPFS,该方法通过保留样本间的相似性来最大化降维空间中类别之间的分离性，所以对于类间的相关性信息也具有一定的保留性能.

Table 9 Average Residual Class Correlation Information in the Feature Subset Selected by Each Method

表9 各方法选出的特征子集的平均残留类间相关性信息量

5 结束语

本文研究了多任务特征选择问题.目前流行的特征选择方法面临单变量度量不能保证全局最优、无法降低特征间分类冗余性及无法保留原空间类别之间的相关性等难题.本文提出一种保留分类信息的特征子集选择方法CIP，并通过多任务学习技术进行了实现，由此解决了以上3个问题.实验结果表明:CIP在各类数据上均取得较好的效果.

[1]Xu Yan, Li Jintao, Wang Bin, et al. A category resolve power-based feature selection method [J]. Journal of Software, 2008, 19(1): 82-89 (in Chinese)(徐燕, 李锦涛, 王斌, 等. 基于区分类别能力的高性能特征选择算法[J]. 软件学报, 2008, 19(1): 82-89)

[2]Guyon I, Elisseeff A. An introduction to variable and feature selection [J]. Journal of Machine Learning Research, 2003, 3: 1157-1182

[3]Duan Jie, Hu Qinghua, Zhang Lingjun, et al. Feature selection for multi-label classification based on neighborhood rough sets [J]. Journal of Computer Research and Development, 2015, 52(1): 56-65 (in Chinese)(段洁, 胡清华, 张灵均, 等. 基于邻域粗糙集的多标记分类特征选择算法[J]. 计算机研究与发展, 2015, 52(1): 56-65)

[4]Zhao Zheng, Wang Lei. Liu Huan, et al. On similarity preserving feature selection [J]. IEEE Trans on Knowledge and Data Engineering, 2013, 25(3): 619-632

[5]Zhang Yin, Zhou Zhihua. Multi-label dimensionality reduction via dependence maximization [J]. ACM Trans on Knowledge Discovery from Data, 2010, 4(3): Article 14

[6]Zhao Jidong, Lu Ke, He Xiaofei. Locality sensitive semi-supervised feature selection [J]. Neurocomputing, 2008, 71(101112): 1842-1849

[7]Gu Quanquan, Li Zhenhui, Han Jiawei. Generalized fisher score for feature selection [C]Proc of the 27th Int Conf on Uncertainty in Artificial Intelligence. Arlington, VA: AUAI, 2011: 266-273

[8]Nie Feiping, Xiang Shiming, Jia Yangqing. Trace ratio criterion for feature selection [C]Proc of the 23rd AAAI Conf on Artificial Intelligence. Menlo Park, CA: AAAI, 2008: 671-676

[10]Zhao Zheng, Wang Lei, Liu Huan. Efficient spectral feature selection with minimum redundancy [C]Proc of the 24th AAAI Conf on Artificial Intelligence. Menlo Park, CA: AAAI, 2010: 673-678

[11]Feng Lin, Wang Jing, Liu Shenglan, et al. Multi-label dimensionality reduction and classification with extreme learning machines [J]. Journal of Systems Engineering and Electronics, 2014, 25(3): 502-513

[12]Zhang Mingling, Zhou Zhihua. A review on multi-label learning algorithms [J]. IEEE Trans on Knowledge and Data Engineering, 2014, 26(8): 1819-1837

[13]Li Yufeng, Huang Shengjun, Zhou Zhihua. Regularized semi-supervised multi-label learning [J]. Journal of Computer Research and Development, 2012, 49(6): 1272-1278 (in Chinese)(李宇峰, 黄圣君, 周志华. 一种基于正则化的半监督多标记学习方法[J]. 计算机研究与发展, 2012, 49(6): 1272-1278)

[14]Zheng Wei, Wang Chaokun, Liu Zhang, et al. A multi-label classification algorithm based on random walk model [J]. Chinese Journal of Computers, 2010, 33(8): 1418-1426 (in Chinese)(郑伟, 王朝坤, 刘璋, 等. 一种基于随机游走模型的多标签分类算法[J]. 计算机学报, 2010, 33(8): 1418-1426)

[15]Liu Shenglan, Feng Lin, Qiao Hong. Scatter balance: An angle-based supervised dimensionality reduction [J]. IEEE Trans on Neural Networks and Learning Systems, 2014, 26(2): 277-289

[16]Tang Jiliang, Alelyani S, Liu Huan. Feature selection for classification: A review [G]Data Classification: Algorithms and Applications. Boca Raton, FL: CRC, 2014: 37-64

[17]Liu Jun, Ji Shuiwang, Ye Jieping. Multi-task feature learning via efficient l2,1-norm minimization[C]Proc of the 25th Int Conf Uncertainty in Artificial Intelligence. Arlington, VA: AUAI, 2009: 339-348

[18]Argyriou A, Evgeniou T, Pontil M. Convex multi-task feature learning [J]. Machine Learning, 2008, 73(3): 243-272

[19]Gong Pinghua, Ye Jieping, Zhang Changshui. Multi-stage multi-task feature learning [J]. Journal of Machine Learning Research, 2013, 14: 2979-3010

[20]Xiao Yunhai, Song Huina. An inexact alternating directions algorithm for constrained total variation regularized compressive sensing problems [J]. Journal of Math Imaging Vision, 2012, 44: 114-127

[21]Peng Hanchuan, Long Fuhui, Din Chris. Feature selection based on mutual information criteria of max-dependency, max-relevance, and min-redundancy [J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2005, 27(8): 1226-1238

[22]Xu Junling, Zhou Yuming, Chen Lin, et al. An unsupervised feature selection approach based on mutual information [J]. Journal of Computer Research and Development, 2012, 49(2): 372-382 (in Chinese)(徐峻岭, 周毓明, 陈林, 等. 基于互信息的无监督特征选择[J]. 计算机研究与发展, 2012, 49(2): 372-382)

[23]Wei Jinmao, Wang Shuqin, Yuan Xiaojie. Ensemble rough hypercuboid approach for classifying cancers [J]. IEEE Trans on Knowledge and Data Engineering, 2010, 22(3): 381-391

Wang Jun, born in 1981. PhD candidate. Her main research interests include pattern recognition and machine learning (junwang@mail.nankai.edu.cn).

Wei Jinmao, born in 1967. Professor and PhD supervisor. His main research interests include machine learning, data mining, Web mining, and bioinformatics.

Zhang Lu, born in 1989. Master. Her main research interests include machine learning and natural language processing (luzhang@mail.nankai.edu.cn).

Multi-Task Feature Learning Algorithm Based on Preserving Classification Information

Wang Jun, Wei Jinmao, and Zhang Lu

(CollegeofComputerandControlEngineering,NankaiUniversity,Tianjin300071) (CollegeofSoftware,NankaiUniversity,Tianjin300071)

In pattern recognition, feature selection is an effective technique for dimension reduction. Feature evaluation criteria are utilized for assessing the importance of features. However, there are several shortcomings for currently available criteria. Firstly, these criteria commonly concentrate all along on class separability, whereas class correlation information is ignored in the selection process. Secondly, they are hardly capable of reducing feature redundancy specific to classification. And thirdly, they are often exploited in univariate measurement and unable to achieve global optimality for feature subset. In this work, we introduce a novel feature evaluation criterion called CIP (classification information preserving). CIP is on the basis of preserving classification information, and multi-task learning technology is adopted for formulating and realizing it. Furthermore, CIP is a feature subset selection method. It employs Frobenius norm for minimizing the difference of classification information between the selected feature subset and original data. Also l2,1 norm is used for constraining the number of the selected features. Then the optimal solution of CIP is achieved under the framework of the proximal alternating direction method. Both theoretical analysis and experimental results demonstrate that the optimal feature subset selected by CIP maximally preserves the original class correlation information. Also feature redundancy for classification is reduced effectively.

feature selection; multi-task learning; classification information preserving; feature redundancy; proximal alternating direction method

2015-11-09；

2016-04-13

国家自然科学基金项目(61772288，61070089)；天津市自然科学基金项目(14JCYBJC15700)
This work was supported by the National Natural Science Foundation of China (61070089) and the Natural Science Foundation of Tianjin of China (14JCYBJC15700).

TP181; TP391