基于基本果蝇算法改进的数据库查询优化策略

陈金萍

（大连海洋大学 应用技术学院，辽宁 瓦房店 116300）

基于基本果蝇算法改进的数据库查询优化策略

陈金萍

（大连海洋大学 应用技术学院，辽宁 瓦房店 116300）

由于当前很多常用的数据库查询优化算法都存在查询效率低的问题，很难找到能够实现全局最优的数据库查询优化算法，使得很多用户在进行数据库查询时，数据库无法完全满足其需求.为此，本文提出了一种基于基本果蝇算法改进的数据库查询优化方法，并通过仿真测试的方法验证其查询优化的效果，以求加快数据库查询优化问题的效率和质量.

两阶段；优化方案；数据库查询；果蝇算法；仿真测试；查询优化

在数据库应用中，查询是其中使用最为频繁的操作.查询操作需要在动态组成的虚拟数据库上进行，在查询过程中，服务是中心，整个查询过程通过动态组建服务以供用户使用并完成查询任务.随着信息技术的发展，数据库在信息管理系统中的重要性与日俱增升，要想为用户提供更好的信息管理系统功能，就必须使用优化的查询方案，以获得更好的使用体验.

1 数据库查询优化研究简介

传统的数据库查询方法一般而言都是通过依靠人工输入对应的指令的方式来实现的，但是这种方式的自动化水平较低，使用效率十分不理想，无法完全满足现代信息管理系统的查询需求.在此背景下，很多研究人员又提出了一些查询算法，如基于例子全优化算法、萤火虫算法等，但是虽然寻找全局最优解的能力都很强，并且还兼带搜索能力，都能以最快的速度找到最优方案，也因此而成为数据库优化研究分析中的一个重要方向方向.但是这些算法都依然存在一些缺点，例如，后期收敛速度较慢，容易陷入局部最优查询方案等，也未能成为最优方案.因此，必须对这些缺陷进行弥补，找到更加卓越的数据库查询优化策略.

为了获得更好的数据库查询优化方案，笔者在本文中提出了一种两阶段数据库查询优化策略，这种优化策略主要被分为两个阶段进行.第一个阶段是对基本的果蝇优化算法进行一定的改进，并将其运用到数据库查询优化中；第二阶段，对数据库的查询问题进行更深一步的优化，最后通过仿真对比试验验证其有效性，下面将对该数据库查询优化方案的优化过程进行具体的叙述.

2 基本果蝇算法改进分析

2.1 基本果蝇优化算法介绍

果蝇优化算法是一种新型的群智能算法，与其他群智能算法相比较来说，具有能够调整参数和简单容易实现的优点，学习和理解起来更加容易.该算法的具体过程如下所示：参数初始化——设置果蝇个体嗅觉觅食的随机方向和距离——估计与远点的距离，并计算下一位置的味道浓度判定值——将下一位置浓度的判定值带入味道浓度判定值函数，再将果蝇个体所在位置的味道浓度计算出来——计算出整个群体中味道浓度最佳的果蝇——记录最佳味道浓度值预期对应的坐标，这是，果蝇群体就会依靠其敏锐的视觉飞向该坐标——持续重复上述几个步骤，直到所得结果满足终止条件为止.

2.2 现存的基本果蝇算法中存在的缺陷分析

该算法的工作原理和粒子群优化算法十分相似，需要对果蝇种群进行初始化处理，再依据移动的步长大小来更新果蝇种群的位置，之后果蝇种群中的其他个体逐步向适应度最优的个体的位置集中，并同时更新新种群果蝇的位置.这种优化方式的不足可以简述为两点：第一点，通过让种群向当前最优位置的个体移动的方式进行种群的位置更新，容易使当前的最优个体陷入局部极值.而且缺乏有效可用的机制来跳出局部极值的局限，种群的进化就会停止，以致无法找到问题的全局最优解.第二点，果蝇群体的进化过程都是通过固定步长的方式来实现的，如果固定步长设置得较大，果蝇就容易偏离最优解，而且这种方式其过程的稳定性较差，后期容易出现振荡的不良现象.但是如果固定的步长设置过短，又会导致果蝇群体陷入局部最优解的恶性循环，使得算法的收敛精度达不到要求.因此，针对该算法的缺陷，笔者提出了一种效果更佳的优化算法.

2.3 基本果蝇算法的优化分析

（1）步长自适应调整：在算法的初期，保持一个较大的步长；进入迭代的后期，就可以移动该步长，将自适应步长减小，进一步加快收敛的速度，同时获得更高精度的全局最优解.

（2）味道浓度判定值的修正：笔者在Si上加入一个参数，通过该参数的加入使得果蝇种群摆脱局部最优解的局限，进一步达到找出全局最优解的目的.

（3）改进后的果蝇算法稳定性和鲁棒性更强，查询问题的求解速度的得到了巨大的提升，同时还能获得更加精确的收敛精度.从根本原因分析，这主要是因为改进后的算法使用上一代最优味道浓度判断值和当前的迭代次数自适应调整进化步长，进化到后期时，反而因此获得了更好的收敛精度解，再通过对味道浓度判定值进行的修正避免其陷入局部最优解.

3 基于基本果蝇算法改进的数据库查询优化策略分析

3.1 数据库查询优化的数学模型

在数据库的查询优化过程中，查询优化的方案多种多样，那么如何在这些方案中选出最优的查询方案十分重要，直接决定了数据库查询结果的精确度和查询的效率是否能满足用户的需求.因此，本文使用两阶段策略，找到了最优的数据库查询方案.使用“左深树”为搜索策略空间.对于一个连接为J=RioinS的计算代价cost(J)而言，其计算式子如下图一所示，在该式子当中V（c，R）的计算式子如图二所示.

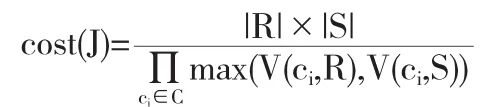
图一 计算代价式子

图二 V（c，R）的计算式子

3.2 本文所述数据库查询优化问题的求解过程

第一步，对一个数据库的查询问题的左深树进行编码，以便进一步得到数据库的查询序列L.第二步，对果蝇优化算法的相关参数进行初始化处理，相关参数有最大迭代次数以及群体的规模等.第三步，以得到的数据库查询序列L初始化的果蝇群体位置Si，再通过下图三所示的式子计算出果蝇群体的适应度值smelli，之后得到的果蝇的种群个体的状态就是对应的数据库查询的结果.第四步，在果蝇种群之中，找出味道浓度最佳的果蝇，并将其对应的浓度值和对应序列的Si保留下来.第五步，更新整个算法过程的判定值，果蝇群体飞向最优位置.第六步，不断重复上述的几个步骤，当迭代次数达到最大值时，果蝇群体的最优位置就正好对应了数据库查询方案.完成上述步骤之后，还需进行最后一步，即通过遗传算法更进一步地进行数据库优化查询，从而找到最优的方案，实现两阶段的数据库最优查询.

图三 适应度函数定义式（其Si为个体i在t迭代中的序列编码）

4 仿真实验介绍及结果分析

4.1 仿真实验环境介绍

本文将对上文所叙述的两阶段数据库查询优化策略进行仿真测验，以验证该方法是否能够实现最优查询.本次仿真测选择基本的果蝇算法数据库查询优化策略和粒子群优化算法数据库查询优化策略进行对比分析，依据查询所需的代价、搜索的代价以及查询问题过程中所需的时间作为评价查询结果好坏的评判标准.

4.2 仿真实验结果与分析

4.2.1 代价结果分析

通过对上文所述的算法对数据库的查询优化问题进行求解，得到的搜索代价和查询优化代价结果，对所得的结果进行分析，可得到如下结论：首先，如果数据库的规模相对较小，那么基本果蝇算法、粒子群优化算法以及本文所述的算法之间表现出来的性能差别不会十分明显，都能够得到较为理想的查询结果.其次，随着数据库规模的增大，这三种算法的搜索代价和查询代价都有不同程度的增加，其中本文所述算法增加的幅度较小，变化趋势相对较为稳定.通过对比试验的结果我们可以知道，在这三种算法当中，文本算法的性能优于其他两个算法.

4.2.2 收敛速度和查询效率的比较分析

通过仿真结果可知，随着数据库规模的增大，这三种算法找到最优解所花费的收敛时间逐渐加长，分析其产生原因可知，主要是计算复杂度增加造成的.对于相同大小规模的数据库，本文所述的算法所花费的时间最短，粒子群优化算法所需的时间长度次之，基本果蝇算法所需的求解时间最长.本文所述算法之所以能够取得如此好的效果，主要是因为解决了另外两种算法都存在的问题，即后期收敛速度慢且容易陷入局部最优解，因此本文所述的算法在执行速度上表现出明显的优势.

本文所述方法不仅可以得到数据库查询优化问题中的最优解，而且相对于稳重所提到的其他算法而言，具有更好的查询效率和查询质量，这对信息管理系统来说无疑是一个巨大的进步，在实际使用中的应用前景十分广阔.

5 结语

综上所述，本文针对基本果蝇优化算法及其数据库查询优化算法存在的效率低下、难以找到全局最优解的缺点，进行了优化，并提出了一种收敛效果佳、查询速度及结果更合理的数据库查询优化策略.通过对果蝇优化算法进行的修正，弥补了基本果蝇优化算法的不足，再通过遗传算法进行查询，进而得到最优解.这种算法能够加快数据库查询优化问题的速度和效率，而且使用质量更有保证.但是科技的进步步伐从未停止，更快更好的数据库查询优化策略一定存在，还需要研究人员的不断努力.

〔1〕曾理.数字有机体数据库分布式查询优化与分布式事务处理的研究与实现[J].电子科技大学，2009，4（1）：98-99.

〔2〕李芳萍.基于半连接策略的分布式数据库查询优化理论研究及应用[J].中南大学,2008,6（30）：94-95.

〔3〕张琛.网络数据库查询优化策略的研究.[D].华中科技大学，2007，6（1）：59-60.

〔4〕宋丽娜.基于遗传退火算法的数据库多连接查询优化研究与应用[J].长春理工大学，2009，6（1）：98-99.

TP18

A

1673-260X（2017）03-0031-02

2016-12-11