概念知识系统与闭包系统的联系

洪小飞，袁晓华

（郑州工业应用技术学院 基础部，河南 郑州 451100）

概念知识系统与闭包系统的联系

洪小飞，袁晓华

（郑州工业应用技术学院 基础部，河南 郑州 451100）

形式背景中的概念来源于哲学，是由外延以及内涵共同形成的.为实现概念的发现、排序和显示的目的，德国数学家Will.R首次提出以形式背景为基础构建格理论的思想，该理论成为数据分析、知识处理的重要方法.本文首先给出概念知识系统的概念，通过论证得到：形式背景与概念知识系统能互相确定，而且且建立概念知识系统与闭包系统之间的联系.

形式背景；概念知识系统；闭包系统

1.1 预备知识

定义1.1.1[1]（上界与下界） 设(X,≤)为一偏序集，A⊆X，若∀a∈A，都有x≤a，x∈X，则称x是A的一个下界；若∀a∈A，都有a≤y，y∈X，则称y是A的一个上界.A的所有下界的集合中最大的下界称为A的下确界；A的所有上界的集合中最小的上界称为A的上确界.A的下确界可记为infA或∧A；A的上确界可记为supA或∨A.若A中只有两个元素x,y时，可记为x∨y及x∧y.

定义1.1.2[1]（格与完备格） 设(X,≤)是一个偏序集，若∀x,y∈X，x∨y和x∧y都存在，则称 (X,≤)是一个格.若∀A⊆X，supA或∨A及infA或∧A都存在，则称(X,≤)是一个完备格.

定义1.1.3[2]（形式背景） 称(U,A,I)为一形式背景，其中U={u1,u2,…,un}称为对象集，且每个ui(i=1,2,…,n)为一个对象，A={m1,m2,…,mm}称为属性集，且每一个mj(j=1,2,…,m)为一个属性，I为U与A的二元关系，即I⊆U×A.

在形式背景(U,A,I)中，若u具有属性m，用(u,m)∈I来表示，简记做uIm，一般用1表示(u,m)∈I，0表示(u,m)∉I.如此，一个形式背景(U,A,I)可用只含0,1的二维表来表示.

例1.1.1 如下一个二维表可表示一个形式式背景.

?

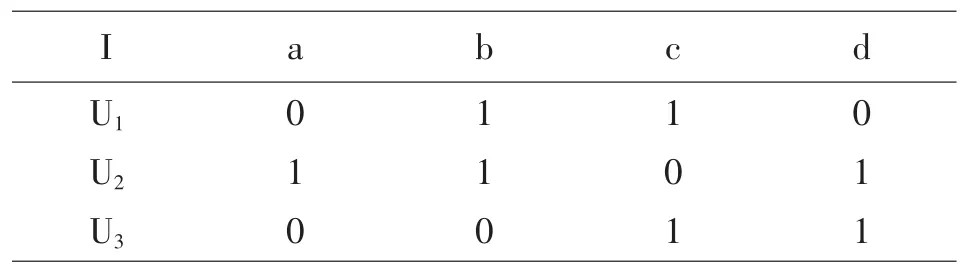
在该形式背景中，U={u1,u2,…,un}，A={a,b,c,d}，由表显然可知(u2,a)∈I，(u1,a)∉I等.

定义1.1.4[3]设(U,A,I)为一形式背景，X⊆U,B⊆A.下面给出一对对偶算子，分别记作f,g,

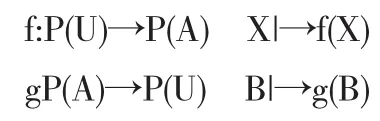
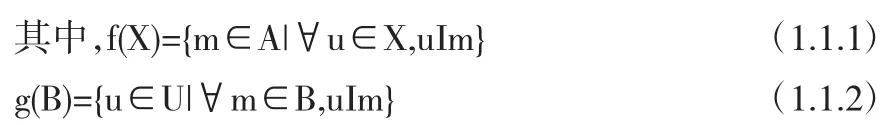
f(X)表示集合X中所有对象共的属性集，g(B)表示集合中所有属性的对象集.

定义1.1.5[4]（正则形式背景） 设(U,A,I)为一形式背景，称(U,A,I)为正则形式背景，若满足下列条件：

事实上，如果一形式背景(U,A,I)可称为为正则形式背景，那么该形式背景所对应的二维表中每一行和列中至少有一个0或1，并且不允许行与列均为0与1.

一般情况下，本文所使用的形式背景(U,A,I)均是正则形式背景.

命题1.1.1[4]设(U,A,I)是一形式背景，∀X1,X2X⊆U,B1, B2,B⊆A，有以下结论成立：

定义1.1.6[2]（概念）设(U,A,I)是一形式背景，X⊆U，B⊆T，称（X，B）为形式背景（U，A，I）的一个概念，若满足以下条件：

一般情况下，本文用L(U,A,I)来表示形式背景(U,A,I)的所有概念的集合.即L(U,A,I)={(X,B)|f(X)=B,g(B)=X}.

例1.1.2 如例1.1.1所示形式背景，则所有的概念有：

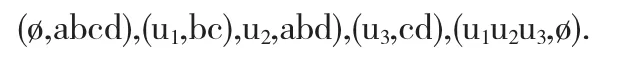
命题1.1.2 设(U,A,I)是一形式背景，则(L(U,A,I),≤)为一偏序集,且是一个完备格，称为概念格.

其次，再证(L(U,A,I),≤)是一个格.∀(X1,B1),(X2,B2)∈L(U, A,I)，往证

如果(X,B)是(X1,B1)和(X2,B2)的任一个共同下界，则X⊆X1且X⊆X1，从而X⊆X1∩X2，所以(X,B)≤(X1∩X2，f(g(B1∪B2)))，即

同理可得(X1,B1)∨(X2,B2)=(g(f(X1∪X2)),B1∩B2)∈L(U,A,I).

因此，(L(U,A,I),≤)是一个格.

用上述方法，可证∀(Xt,Bt)∈L(U,A,I),t∈T，有

综上所诉，(∈L(U,A,I),≤)是完备格.

定义1.1.7[5]设U是一个有限对象集，A为有限属性集，X1,X2⊆U，B1,B2⊆A.称L:P(U)→P(A)为外延内涵算子，若L满足：

称H:P(A)→P(U)为内涵外延算子，若H满足：

称(U,A,L,H)为概念知识系统.

定理1.1.1[5]设(U,A,L,H)为概念知识系统，X1,X2⊆U，B1,B2⊆A,则有以下新性质成立：

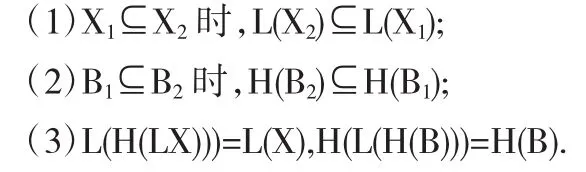
定义1.1.8[6]设(U,A,L,H)为概念知识系统，对于X⊆U, B⊆A，若L(X)=B,H(B)=X，称(X,B)为概念.

定理1.1.2[5]设(U,A,L,H)为一个概念知识系统,则(L(U, A,L,H)≤)是一个完备格，称为概念知识格.

其中L(U,A,L,H)={X,B)|L(X)=B,H(B)=X,X⊆U,B⊆A}.

定义1.1.9[1]（闭包系统） 设S是一个集合，ℜ是S的子集的集合，ℜ⊆2S，若ℜ满足：

（1）S∈ℜ；

（2）P⊆ℜ，则∩P∈ℜ；

则称ℜ是一个闭包系统.

定义1.1.10[1]（闭包算子） 设S是一个集合，φ：2S|→2S，满足：

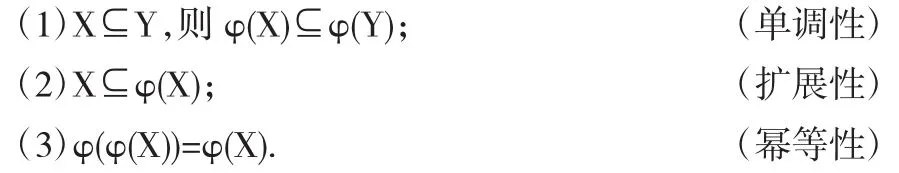
则称φ是S上的一个闭包算子.

1.2 概念知识系统与形式背景

命题1.2.1 设(U,A,I)为形式背景，集合U和A均为有限的，则存在概念知识系统(U,A,f,g)，使得(U,A,f,g)产生的形式背景与(U,A,I)一致.

证明 对形式背景(U,A,I)，设X⊆U,B⊆A，取

f(X)={a∈A:∀x∈X,(x,a)∈I}，g(B)={x∈U:∀a∈B,(x,a)∈I}；由定义1.1.7，则显然可证：f满足外延外延内涵算子的条件，g满足内涵外延算子的条件，且由命题1.1.1有g(f(X))⊇X,f(g(B))⊇B.

因此，(U,A,f,g)是概念知识系统.

设I0={(x,a)∈U×A:x∈g({a})}是(U,A,f,g)产生的形式背景(U,A,I0)的二元关系，则I0⊆U×A.且由形式背景(U,A,I)中关系I可知：

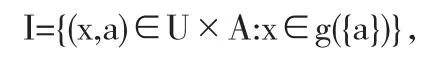
与I0的定义一致，所以，(U,A,f,g)产生的的形式背景(U,A,I0)与(U,A,I)一样.

命题1.2.2 设(U,A,L,H)为概念知识系统，那么存在形式背景(U,A,I)，使得(U,A,I)产生的概念知识系统与(U,A,L,H)一致.

根据定义1.1.7（1.7）式，∀u∈U,{u}≠ø⇒L(u)≠A，即f(u)≠A；由定义1.1.7（1.1.9）式∀m∈A,{m}≠ø⇒H(m)≠U，g(m)≠U即.当U≠{u}时，L(u)≠L(U)=ø，即f(u)≠ø；同理可证，当A≠{m}时，H(m)≠H(A)=ø，即g(m)≠ø.所以，(U,A,I)为一正则形式背景.

由上述两定理可知，形式背景(U,A,I)和概念知识系统(U, A,L,H)可以相互确定，并且L(U,A,I)中的概念与L(U,A,L,H)中的概念一致，即L(U,A,I)=L(U,A,L,H)，那么本节中的概念知识格可简称为概念格，且L(U,A,L,H)可记为L(U,A,f,g)，本文之后用(U,A,f,g)来表示概念知识系统.

1.3 概念知识系统与闭包系统

命题1.3.1 算子(fg)为U上的闭包算子，算子(gf)为A上的闭包算子.

证明 （1）如果X⊆Y，且X,Y⊆U，则由f,g闭包算子的属性可得：f(X)⊇f(Y)，g(f(X))⊆g(f(Y))，即(fg)(X)⊆(fg)(Y),单调性成立；

（2）由定义1.1.7知：X⊆g(f(X))，即X⊆(fg)(Y)，扩展性成立；

（3）由定理1.1.1（3）知对任意的X⊆U，有f(g(f(X)))=f(X)，从而有g(f(g(f(X))))=g(f(X))，即(fg)(fg)(X)=(fg)(X)，幂等性成立.

综上所述，算子(fg)为U的闭包算子.

同理可证，算子(gf)为A的闭包算子.

命题1.3.2 设(U,A,f,g)是概念知识系统，ℜ是U上的闭包系统，ℑ是A上的闭包系统，定义

（1）φ:P(U)→P(U)，φ(X)=∩{T∈ℜ|X⊆T}；

（2）ø:P(A)→P(A)，ø(B)=∩{T∈ℑ|B⊆T}.

则φ是U上的闭包算子，ø是A上的闭包算子，这两个算子均称为由闭包系统诱导出的闭包算子.

证明 （1）首先，如果X⊆U，则{T∈ℜ|X⊆T}⊇{T∈ℜ|Y⊆T}，从而有：∩{T∈ℜ|X⊆T}⊆∩{T∈ℜ|Y⊆T}，即φ(X)⊆φ(Y),单调性成立.

其次，由于{T∈ℜ|X⊆T}中的每个元素都包含X，故可得：X⊆∩{T∈ℜ|X⊆T}=φ(X)，从而X⊆φ(X)，扩展性得证.

再次，因为{T∈ℜ|X⊆T}中的每一个元素都是闭包系统ℜ中的元素，且ℜ是闭包系统，故∩{T∈ℜ|X⊆T}也为ℜ的元素，记∩{T∈ℜ|X⊆T}=Y，则Y∈ℜ，从而Y∈{T∈ℜ|Y⊆T }，所以，∩{T∈ℜ|Y⊆T}=Y，又由算子的扩展性可得Y⊆φ(Y) =∩{T∈ℜ|Y⊆T}，即φ(Y)=Y，故φ(φ(X))=φ(Y)=Y，从而可以得到φ(φ(X))=φ(X)，即幂等性得证.

综上所述，φ是U上的闭包算子.

同理可证（2）.

命题1.3.3 设(U,A,f,g)为概念知识系统，则

（1）{(fg)(X)|X⊆U}是U上的闭包系统；

（2）{(gf)(B)|B⊆A}是A上的闭包系统.

证明 （1）首先，因为(U,A,f,g)为概念知识系统，从而对∀X⊆U，都有g(f(X))⊇X成立，所以有(fg)(X)⊇X,即X⊆(fg) (X)；由于U⊆U，则U⊆(fg)(U)，从而U∈{(fg)(X)|X⊆U}.

其次，假设P⊆{(fg)(X)|X⊆U}，则由命题1.3.1闭包算子(fg)的扩展性可知：∩P⊆(fg)(∩P)，另外，对∀T∈P，均有∩P⊆T；再由闭包算子(fg)单调性有：

从而T∈P⊆{(fg)(X)|X⊆U)}；所以存在X0，使得T=(fg) (X0)，于是有：

将（1.13）代入（1.12）得(fg)(∩P)⊆(fg)(T)=T，即(fg)(∩P)⊆T.由于T是P的任一元素，所以(fg)(∩P)⊆P,又由于有∩P⊆(fg)(∩P)，从而可得(fg)(∩P)=∩P.

综上可得，∩P⊆(fg)(∩P)∈{(fg)(X)|X⊆U}.

所以，∩P∈{(fg)(X)|X⊆U}.

所以，{(fg)(X)|X⊆U}是U上的闭包系统.

同理可证（2），即{(fg)(B)|B⊆A}是A上的闭包系统.

命题1.3.4 设(U,A,f,g)是概念知识系统，

（1）记ℜ={(fg)(X)|X⊆U}，ℜ是对象U上的一个闭包系统，则(ℜ,⊆)是一个完全格；

（2）记ℑ={(fg)(B)|B⊆A}是属性A上的闭包系统，则(ℑ,⊆)是一个完

全格.

证明 （1）首先，∀P⊆ℜ，P中的每一个元素N，均有∩P⊆N成立，所以∩P是集合P的下界；假设集合M是P的任一下界，则M是P的每一个元素的子集，则∀m∈M，均有m∈∩P，即M⊆∩P，从而∩P是集合P的下确界.

其次，对于集合{X∈ℜ|∪P⊆X}，则{X∈ℜ|∪P⊆X}是ℜ中P的上界的集合，那么有∩{X∈ℜ|∪P⊆X}是ℜ中P的上界集合中最小的元素；又由ℜ是闭包系统知∩{X∈ℜ|∪P⊆X}∈ℜ；所以，∩{X∈ℜ|∪P⊆X}是P的上确界.

综上所述，ℜ的任一子集都存在上确界、下确界，故(ℜ,⊆)是完全格.

同理可证（2）.

〔1〕马垣，曾子维，迟呈英，吴建胜.形式概念及其新进展[M].北京:科学出版社,2011.1-13.

〔2〕Nourine L,Raynaud O.A fast algorithm for building lattices[J].Information processing letters,1999,71(5): 199-204.

〔3〕Faïd M,Missaoi R,Godin R.Mining complex structures using context concatenation in formal concept analysis[C]//International KRUSE Symposium,Vancouver,BC.1997:11-13.

〔4〕张文修,魏玲,祁建军.概念格的属性约简理论与方法[J].中国科学(E辑),2005,35(6):628-639.

〔5〕仇国芳,陈劲.概念知识系统与概念信息粒格[J].工程数学学报,2005,22(6):963-969.

〔6〕Valtchev P,Missaoui R,Codin R.et al..Generating frequent itemsets incrementally：Two novel approaches based on galois lattice theory.Journal of Experimental &Theoreyical Artificial Intelligence,2002,14(2-3)：115-142.

O189.1

A

1673-260X（2017）03-0012-03

2016-11-10

2016年湖南财政经济学院课题：我院大学生职业生涯指导-困境与出路（YJ201603）