组合杂交三角形单元的加权能量正交关系

张玲，张伟伟

(西北工业大学 理学院，西安 710129)

组合杂交三角形单元的加权能量正交关系

张玲，张伟伟

(西北工业大学 理学院，西安 710129)

组合变分原理可以增强杂交元方法解的稳定性。建立热传导方程基于区域分解的组合杂交有限元方法，给出单元上温度梯度插值为线性、但温度插值为协调线性插值与非协调二次插值之和的组合杂交三角形单元，并通过数值实验验证理论结果的正确性。结果表明：分片线性温度梯度插值的散度(热源)与非协调温度插值是加权能量正交的；组合杂交三角形元刚度矩阵等同于协调的三角形线性元刚度矩阵，即非协调部分无温度增强特性。

组合杂交元；三角形单元；热传导；能量正交；刚度矩阵；温度增强

0 引 言

随着航空航天、汽车、医疗等领域尖端技术的发展，仅研究材料的力学行为已不能满足实际应用的需求，需要关注材料的多物理场(例如热、力、电、磁)耦合行为[1-3]，因此相关物理量(例如温度、位移等)及其空间梯度、时间变化率等的计算精度都非常重要。

针对热传导-辐射问题，Z.Yang等[4-6]发展了周期及随机复合材料的高阶多尺度分析方法。针对弹性力学问题，T.Zhou[7-8]和聂玉峰等[9]建立了其组合杂交变分原理。作为稳定化的变分原理，为应力离散空间的优化设计提供了很大便利，并成功建立了求解弹性力学问题的高性能四边形单元、六面体单元以及板单元等[10-12]。在探索热力耦合问题[13-15]的高性能组合杂交有限元求解算法之前，有必要先探索热传导问题的有效求解算法。

当材料为各向同性，热传导问题的数学模型简化为Poisson方程。不同于组合杂交矩形元[16]，本文建立Poisson方程的用非协调模式增强温度插值函数的组合杂交三角形元，论证其分片线性温度梯度插值的散度(热源)与非协调温度插值加权能量正交关系。

1 组合杂交变分原理

Poisson方程边值问题为

(1)

(2)

式中：

a(σ,τ)=(σ,τ)Ωm

U=Uc⊕UI

UI|Ωm={span(Bubbles)}

α为组合参数，α∈(0,1)；Th为区域Ω的有限元剖分，Th={Ωm}。

对于网格Th，令Γh，Uh为相应区域剖分的有限元离散空间，满足Γh⊆Γ,Uh⊆U，则对上述问题有如下离散形式：

求(σh,uh)∈Γh×Uh，使得

αb2(σh,v)-b1(σh,vI)+(1-α)d(uh,v)=(f,v)

(∀v∈Uh)

(3)

αa(σh,τ)-αb2(τ,uh)+b1(τ,uhI)=0

(∀τ∈Γh)

(4)

2 场函数的插值近似

对单元Ωm，设pi(xi,yi)(i=1,2,3)为三角形单元按逆时针方向排列的三个顶点，(λ1,λ2,λ3)为三角形单元上任一点p(x,y)的面积坐标，Δ为三角形单元面积，直角坐标和面积坐标有如下关系：

λi=(ai+bix+ciy)/(2Δ)

(5)

式中：ai=xjyk-xkyj,bi=yj-yk,ci=xk-xj,i,j,k轮换,i=1,2,3。

温度v=vc+vI的插值函数为

(6)

vI为非协调Bubble，将线性插值丰富为完全二次多项式以提高逼近精度。

温度梯度τ的插值函数为分片线性多项式：

τ=(λ1I2,λ2I2,λ3I2)β

(7)式中：β=[τx(p1)τy(p1)τx(p2)τy(p2)τx(p3)τy(p3)]T，为结点温度梯度参数；I2为2×2的单位矩阵。

为计算方便，定义矩阵Li=[bici]T,i=1,2。

3 刚度矩阵分析

式(4)中测试函数空间Γh是分片定义的，因此在每个单元Ωm上可以由式(4)解出温度梯度σ，即用温度uc和uI表示温度梯度σ，再将σ的表达式带入式(3)，进而可得到单元刚度矩阵。

在单元Ωm上，由式(6)～式(7)可得：

(8)

式中：

将式(8)带入式(4)，由τ的任意性可知：

(9)

根据式(3)推导出单元刚度矩阵：

αb2m(σ,v)-b1m(σ,vI)

(10)

式中：

[0]3×3为零矩阵，即

(11)

式(11)说明分片线性温度梯度插值的散度(热源)与非协调温度插值是能量正交的。

为了得到此单元和协调的三角形线性单元的等价性，还需计算矩阵E，根据式(3)和式(8)可得：

(12)

式中：

综上可得：

αb2m(σ,v)-b1m(σ,vI)+(1-α)dm(u,v)

(13)

式中：

由于单元刚度矩阵的对称性，可得单元刚度矩阵

(14)

式(14)表明三角形单元内部自由度和顶点自由度无耦合，静力凝聚内部自由度后，D11保持不变，仍为协调的线性单元的刚度矩阵，由此证明温度梯度插值为分片线性多项式，温度插值函数为协调的线性部分和非协调部分的二次部分的三角形组合杂交元等价于基于最小势能原理的协调线性三角形单元，非协调温度插值部分无精度增强特性。

4 数值实验

通过算例验证上述分析结果，针对Poisson方程，即f=0，采用组合杂交元进行计算，并与线性元计算结果进行比较。外边径固定温度为5K，内边径给定热流密度为10W/m2，热传导系数为20W/(m·K)，参考点为内边径上任意一点，真解为6.648。计算区域为圆环，内径是3m，外径是9m[18]。剖分如图1所示，计算结果如表1所示。

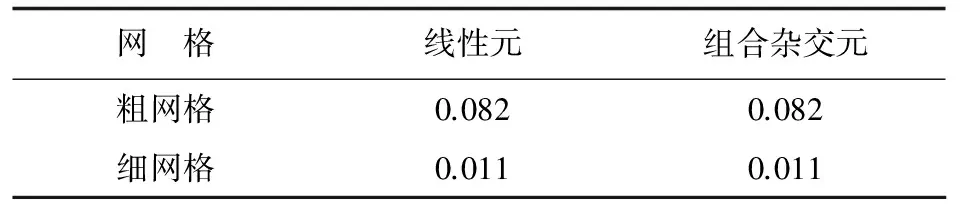
表1 温度绝对误差

从表1可以看出：线性元与本文建立的组合杂交元计算温度相同，数值结果与理论结果一致。

线性元在粗网格和细网格下的温度分布如图2所示。

从图2可以看出：温度沿半径由内向外降低，在内边径达到最大值。

线性元在极细网格下沿x方向和y方向的热流分布如图3所示。

从图3可以看出：线性元在极细网格下沿x方向和y方向的热流分布均在内边径处达到最大值。

5 结 论

对于Poisson方程，本文给出了其组合变分原理，并分析论证了组合杂交三角形元的加权能量正交关系。与四边形单元所得结论不同，仅分片线性温度梯度插值的散度(热源)与非协调温度插值是能量正交的。此时，组合杂交三角形元刚度矩阵等同于协调的三角形线性元刚度矩阵。构造单元增强精度格式仍需着眼于突破恒等关系D12=[0]3×3。

[1]LiuW,QinY.Multi-physicscouplingmodelofcoalspontaneouscombustioninlongwallgobareabasedonmovingcoordinates[J].Fuel, 2017, 188: 553-566.

[2]SuH,RahmaniR,RahnejatH.Thermohydrodynamicsofbidirectionalgroovedrygassealswithslipflow[J].InternationalJournalofThermalSciences, 2016, 110: 270-284.

[3]BonitoA,DeVoreRA,NochettoRH.Adaptivefiniteelementmethodsforellipticproblemswithdiscontinuouscoefficients[J].SIAMJournalonNumericalAnalysis, 2013, 51(6): 3106-3134.

[4]YangZ,CuiJ,SunY.Transientheatconductionproblemwithradiationboundaryconditionofstatisticallyinhomogeneousmaterialsbysecond-ordertwo-scalemethod[J].InternationalJournalofHeatandMassTransfer, 2016, 100: 362-377.

[5]YangZ,CuiJ,SunY,etal.Multiscaleanalysismethodforthermo-mechanicalperformanceofperiodicporousmaterialswithinteriorsurfaceradiation[J].InternationalJournalforNumericalMethodsinEngineering, 2016, 105(5): 323-350.

[6]YangZ,CuiJ,ZhouS.Thermo-mechanicalanalysisofperiodicporousmaterialswithmicroscaleheattransferbymultiscaleasymptoticexpansionmethod[J].InternationalJournalofHeatandMassTransfer, 2016, 92: 904-919.

[7]ZhouT.Finiteelementmethodbasedoncombinationof“saddlepoint”variationalformulations[J].ScienceinChinaSeriesE:TechnologicalSciences, 1997, 40(3): 285-300.

[8]ZhouT.Stabilizedhybridfiniteelementmethodsbasedonthecombinationofsaddlepointprinciplesofelasticityproblems[J].MathematicsofComputation, 2003, 72(244): 1655-1673.

[9] 聂玉峰, 周天孝, 聂铁军. 三角形单元协调与非协调位移的能量正交关系[J]. 应用数学和力学, 1999, 20(6): 619-624.NieYufeng,ZhouTianxiao,NieTiejun.Theenergyorthogonalrelationbetweenconformingandnon-conformingdisplacementsoftriangularelement[J].AppliedMathematicsandMechanics, 1999, 20(6): 619-624.(inChinese)

[10]ZhouTX,NieYF.Combinedhybridapproachtofiniteelementschemesofhighperformance[J].InternationalJournalforNumericalMethodsinEngineering, 2001, 51(2): 181-202.

[11] 聂玉峰, 周天孝. 高性能八节点六面体组合杂交元[J]. 数值计算与计算机应用, 2003, 24(3): 231-240.NieYufeng,ZhouTianxiao. 8-nodehexahedroncombinedhybridelementwithhighperformance[J].JournalonNumericalMethodsandComputerApplications, 2003, 24(3): 231-240.(inChinese)

[12]ZhouTX,XieXP.Zeroenergy-errormechanismofthecombinedhybridmethodandimprovementofAllman’smembraneelementwithdrillingd.o.f.’s[J].InternationalJournalforNumericalMethodsinBiomedicalEngineering, 2004, 20(3): 241-250.

[13]RenB,QianJ,ZengX,etal.Recentdevelopmentsonthermo-mechanicalsimulationsofductilefailurebymeshfreemethod[J].ComputerModelinginEngineering&Sciences, 2011, 71(3): 253-278.

[14]YangZ,CuiJ.Thestatisticalsecond-ordertwo-scaleanalysisfordynamicthermo-mechanicalperformancesofthecompositestructurewithconsistentrandomdistributionofparticles[J].ComputationalMaterialsScience, 2013, 69: 359-373.

[15]GuanX,YuH,TianX.Astochasticsecond-orderandtwo-scalethermo-mechanicalmodelforstrengthpredictionofconcretematerials[J].InternationalJournalforNumericalMethodsinEngineering, 2016, 108(8): 885-901.

[16] 聂玉峰, 张玲, 王惠玲. 组合杂交Wilson矩形单元的加权能量正交关系[J]. 陕西师范大学学报: 自然科学版, 2014, 42(6): 26-30.

Nie Yufeng, Zhang Ling, Wang Huiling. The weighted energy orthogonal relation of combined hybrid Wilson rectangular element[J]. Journal of Shaanxi Normal University: Natural Science Edition, 2014, 42(6): 26-30.(in Chinese)

[17] Brezzi F, Fortin M. Mixed and hybrid finite element method[M]. Berlin Heidelberg: Springer-Verlag, 1991.

[18] Macneal R H, Harder R L. A proposed standard set of problems to test finite element accuracy[J]. Finite Elements in Analysis and Design, 1985, 1(1): 3-20.

(编辑：赵毓梅)

The Weighted Energy Orthogonal Relation of Combined Hybrid Triangular Element

Zhang Ling, Zhang Weiwei

(School of Natural and Applied Sciences, Northwestern Polytechnical University, Xi’an 710129, China)

Variation principles can enhance the stability of numerical solution with the combined hybrid finite element method. Combined hybrid finite element method of heat transfer equation is built on the basis of the domain decomposition technique. The combined hybrid triangular element, in which the temperature gradient is interpolated by linear polynomials on each element, but the temperature is interpolated by the sum of the linear polynomials and the non-conforming quadratic polynomials, is given. The numerical experiments are carried out to verify the accuracy of the theoretical results. The results indicate that the divergence of piecewise linear temperature gradient interpolation and the non-conforming temperature interpolation are of the weighted energy orthogonal relation. The stiffness matrix of this element is equivalent to the conforming triangular linear element, and the non-conforming parts have no contribution to temperature evaluation.

combined hybrid element; triangular element; heat transfer; energy orthogonal; stiffness matrix; enhanced temperature

2016-12-06；

2016-12-20

国家自然科学基金(11471262，11501450) 西北工业大学博士论文创新基金(CX201524)

张玲,shanshi211@163.com

1674-8190(2017)01-073-05

[O242.21]

A

10.16615/j.cnki.1674-8190.2017.01.011

张 玲(1987-)，女，博士研究生。主要研究方向：热力学问题的高效有限元方法。

张伟伟(1986-)，女，博士，讲师。主要研究方向：自适应并行有限元方法。