基于中国外汇储备的币种结构分析

田凤娟 张永亮

（1六盘水师范学院数学与信息工程学院，贵州六盘水，553001；2安康学院数学与统计系，陕西安康，725000）

截至2015年初，中国外汇储备额已达3.8万亿美元，面对如此高额的储备规模，对我国外汇储备的研究具有一定的现实意义。我国外汇储备的币种结构多种多样，而影响因子最大的几种币种分别为美元、欧元、日元、英镑，其中美元的份额最多。孔立平基于传统的三大模型，得到我国储备的最优币种结构，并给出较为合理的比例（孔立平，2010）。艾之涛从风险管理的角度来考虑我国外汇储备的币种优化问题，但作者仅分析了美元和欧元两种币种的情况，缺乏全面性和代表性（艾之涛，2010）。吴艺芳指出中国外汇储备“总量大，增速快，币种结构单一，储备水平偏高”的现状（吴艺芳，2013)。安平指出，传统的指标缺乏现实意义，他认为大多数学者按传统指标得出结论“中国外汇储备已大幅过量”不合理，按ΙMF标准，中国在外汇储备这方面仅略高于适度（安平，2013）。基于前人所做的研究，引入Copula函数研究币种之间的相关性，并估算其VaR，从而分析币种结构。

1 基础理论

1.1 VaR的定义

VaR即风险价值，其定义为在特定的持有期和一定置信水平下，由于各种因素的影响，持有某种资产可能遭受的最大损失，用概率表示：

式中prob表示资产投资的实际损失低于可能出现的最大损失的概率，1-α为置信水平，通常取值为90%，95%和99%，主要由投资者跟随自己的风险偏好来给定。

1.2 Copula函数的定义

Copula函数，又称连接函数，这里给出Copula函数的数学定义。

定义2.2.1（Nelsen，1998）：一个二元函数C称为Copula，若C:Ι2→I=[0,1]，满足：

Copula函数由椭圆Copula函数族和Archimedean Copula函数族组成。本文主要探讨几种常用的Archimedean Copula函数。

(1)Gumbel Copula，其分布函数表达式为：

(2)Clayton Copula，其分布函数的表达式为：

(3)Morgen Copula，其分布函数的表达式为：

2 我国外汇储备的币种构成

本文将发展中国家外汇储备的币种份额近似地等同于我国的币种份额。可以简单地求出每种货币所占的份额，采用2001～2013年的COFFER数据，选取了美元、日元、英镑、欧元四种货币作为外汇储备的币种结构，通过计算得到发展中国家外汇储备币种结构，如表1所示。

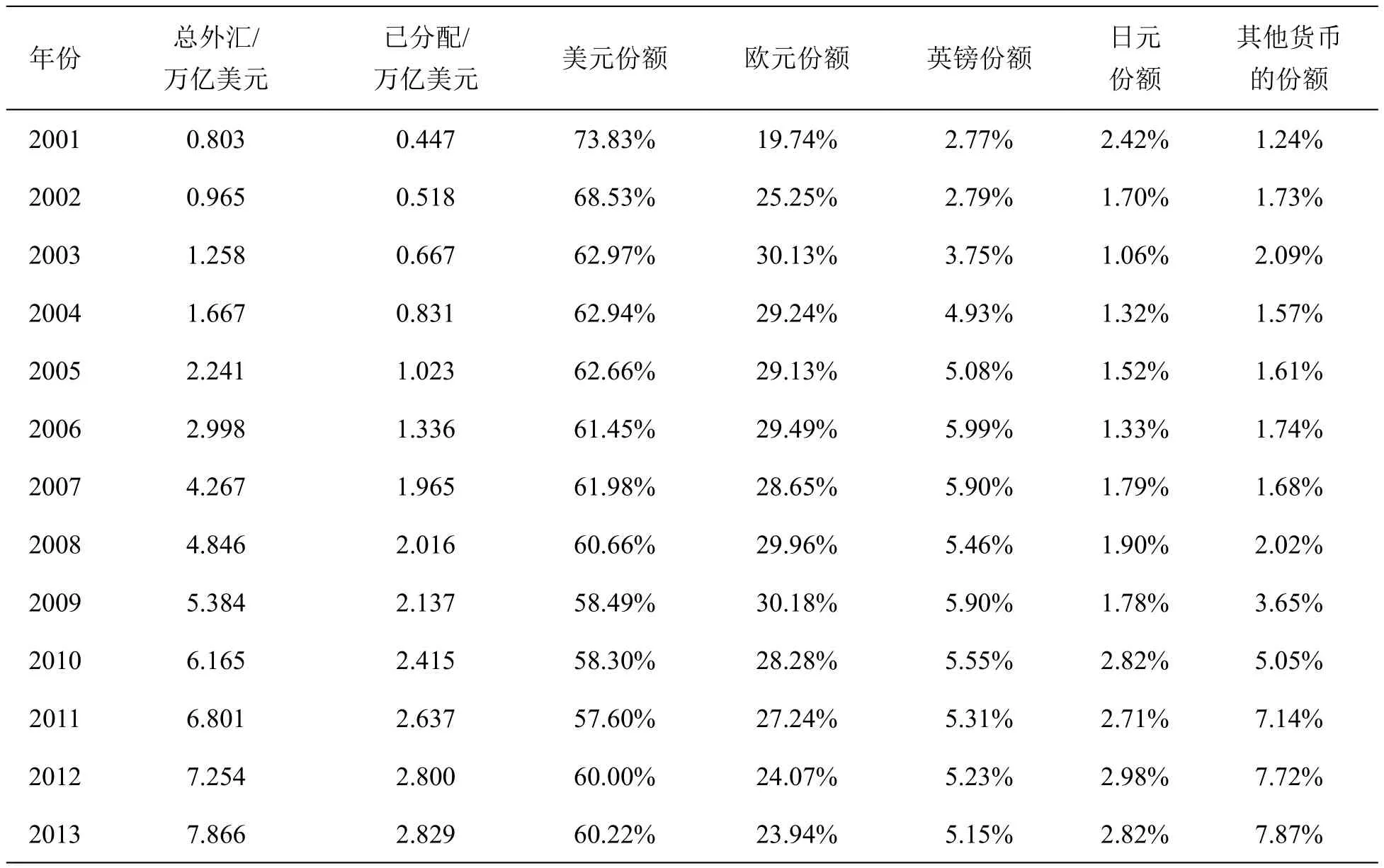
表1 2001～2013年发展中国家的外汇储备币种份额

表1中的数据显示，发展中国家总的外汇储备量处于不断攀升的态势，已分配的外汇储备量也随时间不断地增加，币种构成排序依次为美元＞欧元＞英镑＞日元，其他币种综合的份额逐渐增大。根据表1数据，可以近似给出我国外汇储备的币种组成范围，美元60%～65%，欧元24%～30%，英镑4.5%～6%，日元1.5%～3%，其他币种忽略不计。

3 Copula-VaR法优化币种结构

将我国外汇储备资产看作总资产，各个币种的储备货币资产看作单一资产，选取2007～2013年美元、欧元、日元、英镑兑人民币的每日汇率中间价s，共1 696组数据，求出四种资产的收益率ri,t=lnsi.t-lnsi,t-1（其中ri,t代表第i种货币资产在t时刻的收益率）。收益率波动如图1所示。

图1 四种货币资产的收益率

从图1可见，四种收益率序列均呈现“波动群集”的特点。通过SPSS的统计性描述知，四种资产都呈现尖峰现象，Jarque-Bera统计量显示四种资产收益均不服从正态分布。因此，建立在数据服从正态分布假设之上的求解风险价值的方法，此处无法发挥作用。于是引入Copula函数来提高计算的准确性。

Copula函数的种类较多，在金融数据分析上运用最为广泛的为Archimedean Copula（吴建华等，2014）函数，在此选取Gumbel Copula函数、Clayton Copula函数和Morgen Copula函数来进行分析研究。根据历史数据，首先估计三种函数的参数，由于生成函数ϕ(t)与Kendall秩相关系数τ之间的关系为：

式中ϕ(t)是含参数的函数。下面设三种生成函数ϕ(t)的参数都是，用SPSS软件求得四种资产间的Kendall秩相关系数τ，详见表2所示。

表2 资产收益率相关系数

由表2可知，美元与其他三种资产的相关性是显著的，欧元与英镑也是显著的，只有欧元与日元间的相关关系不够显著。以美元与欧元为例，两者的Kendall秩相关系数τ=0.342，经运算可得函数的参数估计，如表3所示。

γ

表3 参数 的估计值

表4 Archimedean Copula类函数参数估计

表3是四种资产，两两组合下，相应生成函数的参数γ的估计值。γ已知，可以轻松地求出生成函数ϕ(t)的表达式。由表4，我们可以清晰直观地找到每一个Copula的生成函数ϕ(t)，再利用分布函数Kc(t)，

得Gumbel Copula的分布函数为

Clayton Copula的分布函数为

Morgen Copula的分布函数为

已知三种分布函数，如何选取合适的Copula，这里我们利用Kc(t)的性质，做K-S拟合优度检验，即将Kc(t)与均匀分布U(0,1)做检验。结果显示只有Morgen Copula通过K-S检验，而Clayton和Gumbel Copula的P值均不能通过检验，说明Morgen Copula函数可以很好地将美元与欧元两种资产联系起来。根据定义式，Morgen Copula函数的表达式为：

于是，两者的联合分布函数便找到了，即：

现借助Copula计算风险价值，利用历史数据求出美元,欧元，英镑，日元各自的边缘分布，这里用经验分布函数来估计每种资产的边缘分布。对每一组资产价值都做VaR估算，取95%的置信水平，当资产中含有美元时变化较为明显，设美元的权重为p，画出当权重p从0逐渐变化为1的过程中，VaR的变化如图2到图7。

图2 美元权重p与美欧组合的VaR值

图3 美元权重p与美日组合的VaR值

图4 美元权重p与美英组合的VaR值

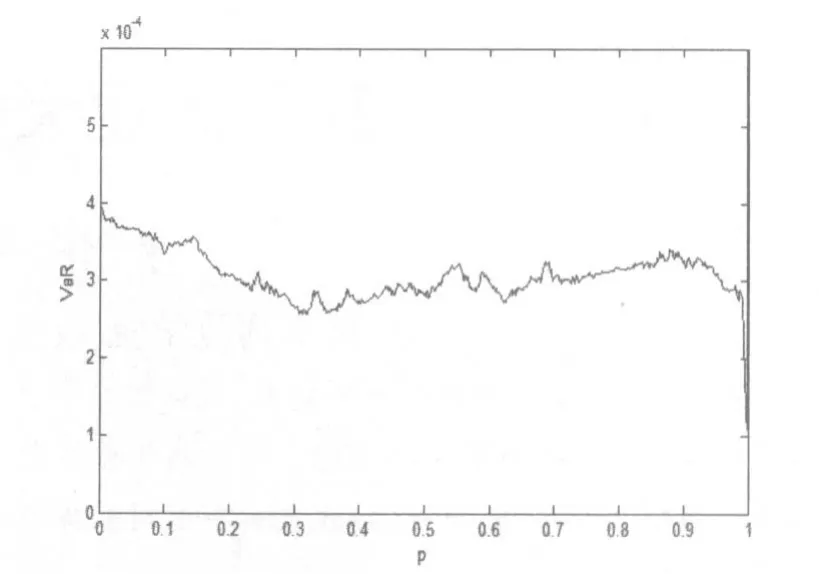
图5 欧元权重p与欧日组合的VaR值

图6 欧元权重p与欧英组合的VaR值

图7 日元权重p与日英组合的VaR值

由权重-风险值图显示，随着美元权重的增大，两种资产组合的VaR逐渐减小，这与实际情况是吻合的。我国实行的货币政策是钉住美元，从之前美元兑换人民币的汇率数据可知，汇率中间价相对于其他三种货币兑人民币的汇率变化幅度小。因此，在资产组合中美元所占的比例越大，总风险越低。但当权重p=1时，外汇储备总资产的VaR值明显变大，可能是因为多种资产组合可以分散风险，只剩下一种资产时，所有的风险都寄托于美元上，一旦美元出现大的调整，这里表现为预测路径的变化，则估计所得美元收益也会大幅变化，对资产价值的影响将不容小觑。当资产组合中不含有美元时，其他三种资产任意组合，VaR的变化趋势较为平稳，局部出现小幅上下波动。值得注意的是，欧元与英镑的资产组合中，当欧元的权重较大时，资产的VaR出现明显的下降趋势。

4 结论

综上分析，我们应增持美元，以降低外汇储备资产的风险，但就收益而言，近年来，美元不断贬值，对收益率有严重的影响，又不应该过多的持有美元资产。根据之前的分析，就我国目前的资产分配现状，美元的份额大约在60%以上，不超过70%，这个比例就资产风险收益来看较为合理，首先60%～70%的份额，使得我国不会面临较大的风险，同时收益方面虽然不高，但多数投资美债有着稳定的收益。本文主要从资产的风险管理方面出发，认为美元资产比例的增加会降低风险。外汇储备作为国家经济重要的一部分，其影响因素多种多样，如政治因素、经济因素等，要全面深入地给出优化的具体策略，仍需综合各个因素，做进一步的研究。

参考文献：

艾之涛.2010.基于VaR方法的我国外汇储备币种结构研究[D].长沙：湖南大学.

安平.2013-9-16(9).中国外汇储备并不多[N].第一财经日报.

孔立平.2010.全球金融危机下中国外汇储备币种构成的选择[J].国际金融研究,(03):64-72.

刘莉亚,王照飞,程天笑.2013.美国国债投资行为的动因分析[J].国际金融研究,(11):36-46.

吴建华,王新军,张颖.2014.相关性分析中Copula函数的选择[J].统计研究,31(10):99-107.

吴艺芳.2013.中国外汇储备问题的思考[J].决策与信息,(05):129-131.

Nelsen R B.1998.An Introduction to Copulas[M].Springer.