用好素材让探究真正发生<br/>——《平行四边形的面积》探究环节问题分析与改进策略

用好素材让探究真正发生
——《平行四边形的面积》探究环节问题分析与改进策略

2017-04-02许冬儿

小学教学设计(数学) 2017年10期

关键词：邻边方格纸方格

许冬儿

《平行四边形的面积》是小学阶段“图形与几何”教学中一个承上启下的重要内容，它上承长方形、正方形面积教学，下接三角形、梯形面积教学，一直被广大一线教师所重视和研究。

一、问题与分析

关于平行四边形面积计算方法探究环节的教学，常常存在以下几个问题：

1.方格使用——机械单一。

在引入环节，教师往往会创设平行四边形与长方形面积大小比较的情境，引导学生用“数方格”的方法去验证面积相等，并告知学生：不满一格都按半格计算。由于长方形、正方形面积计算方法是用摆小方块的方法进行探究的，体现了数学的“度量思想”。将数方格的方法迁移到平行四边形面积计算方法的探究过程中，自然是合理的。然而，平行四边形却不是一个方方正正的图形，这是它和长方形最本质的区别，占用的格子就不可能都是整格的。此时教师如果仅仅给出“不满一格都按半格计算”的机械规定，数的过程就显得十分被动，学生更多关注的只是数的结果，缺乏方法与技巧。甚至还会质疑：不满一格为什么可以按半格计算？这样数出来还准确吗？

这样的数方格形式单一，又缺乏对学生整体性思维的培养，无疑是低效的。

2.操作探究——暗含指令。

在探究平行四边形面积计算方法环节，教师常常会提供平行四边形纸片、剪刀、水彩笔等学具，要求学生以小组活动的形式进行探究并出示活动要求：通过剪一剪、拼一拼，将平行四边形转化成长方形；想一想：平行四边形与拼成的长方形的面积有什么关系？平行四边形的底、高分别与拼成的长方形的长、宽有什么关系？平行四边形面积该怎样计算？

试想，当面对计算平行四边形面积这一新问题时，学生是自觉想到把平行四边形剪拼成长方形的吗？这样的操作活动，学生更多是按照教师的指令去操作，看似很顺利达成目标，但学生的思维却无法得到深入发展。

3.面积公式——不明所以。

在合作探究平行四边形面积计算公式时，教师往往发给每个小组同样的平行四边形纸片，剪拼推导出这个平行四边形面积用“底×高”来计算，然后归纳得出平行四边形面积的计算公式就是“底×高”。这是一个不科学的推理过程，这个平行四边形的面积可以用“底×高”来计算，就能断定所有平行四边形的面积都可以用“底×高”来计算了吗？学生头脑中是会有疑问的。即便教师能追问：“只要沿着其中的一条高剪，所有的平行四边形一定能拼成长方形，大家说是吗？”这也只是形式上的不完全归纳，没有真正引领学生经历不完全归纳的过程。

这样的面积公式探究，学生只知其然，却不知其所以然。

二、改进的策略

1.利用显性素材，为公式推导奠定基础。

这里的显性素材是指教师在课始为每位学生提供的画有一个平行四边形的方格纸。苏教版教材中的例1从比较方格纸上每组中的两个图形面积是否相等入手，引导学生把稍复杂的图形转化成简单的、熟悉的图形，让学生感受转化方法在图形面积计算中的作用，并为进一步的探索活动提供基本思路。例2引导学生通过平移把平行四边形转化为长方形。教材一方面突出了平移在转化过程中的应用，另一方面也鼓励学生用不同方法实现转化的目的。例3的重点则放在探索平行四边形与转化成的长方形之间的联系上，从而推导出平行四边形面积计算方法。值得一提的是，这里的例1、例2的教学都是以方格纸为载体，方格纸作用的发挥也仅仅是数一数验证一下，这样就渗透了转化思想及不同的转化方法。通过例2的转化，学生已能初步从方格图上感悟转化后平行四边形与之前长方形之间各部分的关系，为后面进一步探究平行四边形面积奠定了基础。

笔者摒弃了教材中“不满一格按半格计算”的单纯数格子的方式，而是引导学生在数的过程中自发产生转化的需要，为后续发现转化前后的长方形和平行四边形的关系埋下伏笔。

【教学片断一】

师：看来对于这个平行四边形的面积计算，同学们有两种不同的方法：7×4=28（cm2）；7×5=35（cm2）。要知道哪一种是正确的，我们可以怎么办？

生：数一数格子。

师：如果一个小方格的面积是1cm2，你能数出这个平行四边形的面积是多少平方厘米吗？并且一边数一边把自己是怎么数的表示在方格纸上。

（反馈不同数法）

师：这个平行四边形的面积是多少？看一下同学们都是怎么数的，谁愿意到上面来介绍一下？

生 1：（如下图1）我把左边的三角形分开，移到右边，这样都是整格的了，就能一格一格数了，我数出来有28格，所以是28cm2。

生 2：（如下图2）我也把左边的三角形补到右边变成整格的，数了数每行有7格，有4行，所以一共是 4×7=28（cm2）。

生 3：（如下图3）我是把多出来的这块直角三角形经过平移直接拼到右边，这样平行四边形就拼成了一个长方形。长方形的长是7cm，宽是4cm，所以面积也是 28（cm2）。

生 4：（如下图4）我是沿着中间分开，把右边的梯形平移到左边，也正好拼成长方形，面积也是 7×4=28（cm2）。

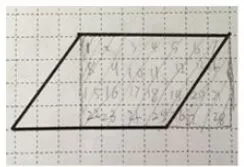
图1

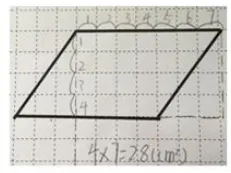
图2

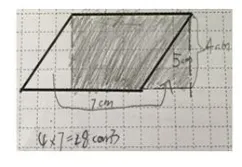
图3

图4

师：这么多种数法，你更喜欢哪一种？说说你的理由。

生5：我更喜欢后面两位同学的方法，他们其实都是把平行四边形割补成了长方形，只要计算长方形的面积就可以了，这样方便。

生6：不过同样是数，生2的数法更“高级”。

师：你的“高级”是什么意思？

生：她没有一格一格数，只数了每行的格数和行数，比生1方便些。

师：那同样是算的方法，生3和生4有什么不一样呢？

生7：生3是沿着顶点出发的高分开，而生4是沿着中间的高分开。

师：除了这两种分法，还有其他的分法吗？你是怎么想的？

生8：我觉得有无数种分法，因为平行四边形有无数条高。

“并且一边数一边把自己是怎么数的表示在方格纸上”的要求把单纯的数格子上升为有不同方法的数格子，激发学生将目光从局部转向整体，促使学生把平行四边形转化成长方形后再数，进而发现算一算就可以了，为后续推导面积公式打下重要的基础。这样使用方格纸无疑是有效的。

2.妙用生成素材，让探究过程科学完整。

【教学片断二】

师：我们已经知道了这个平行四边形面积的计算方法，那是不是所有的平行四边形面积都可以用“底×高”来计算呢？

学生有的说可以，有的说不一定。

师：出现了不同的声音，那接下去我们该怎么办？

生：用形状不同的平行四边形进行验证。

师：好，请你拿出另一张方格纸。

师：就请你自己在方格纸上画一个和刚才完全不一样的平行四边形，也通过割一割、拼一拼来验证它的面积是不是也可以用“底×高”来计算。

学生兴致盎然，画着自己心目中的平行四边形。画完后组织同桌交流，再全班反馈。

这一环节，学生借助方格纸，创造出了各种形状的平行四边形，为进一步理解面积计算公式提供了丰富的素材，并且通过割补都顺利转化成了长方形。从这些丰富的素材中，我们可以感受到，各种平行四边形面积计算方法的推导已深入学生的心，学生已经完全理解平行四边形的面积为什么用“底×高”来计算了，而且引领学生经历了科学的探究过程。这比教师提供给学生不同的平行四边形纸片进行验证要有效、有趣得多。

3.补用变式素材，让公式理解更加全面。

在得出面积计算公式后，笔者又补充了如下两个平行四边形素材。其目的有三：其一，由于前面都是以方格图为载体，但其实练习中、生活中平行四边形的出现一般并不带方格。因此，在借助方格探究出面积计算方法后，引导学生想象这两个平行四边形沿高剪开后将会转化成怎样的长方形是十分必要的。其二，是因为在方格纸上提供或创造的平行四边形，学生习惯沿着格子线画高，因此高都是纵向的。这里提出如图1左右底边上的高有利于打破学生的思维定势，况且寻找左右底边对应的高也是学生面积公式应用的难点。其三，又因为格子图上画出的都是水平放置的平行四边形，割补时只是水平平移，这里给学生提供如图2可以上下平移转化的平行四边形，有助于学生从不同的角度进行转化。