从点、线、面中体会有序的思想方法——《巧数线段、角和三角形》教学设计

刘井金

【教学内容】

人教版二年级上册第一单元《认识线段》及第三单元《角的初步认识》。

【教学过程】

一、由点到线，复习线段

师：这是一条线段，它是由几个端点和一条什么样的线组成的？

预设：2个端点和1条直直的线组成的。

师：现在一共有几条线段呢？

预设：2条（3条）。

师：（追问）2条是怎么数的？3条又是怎样数出来的？

3.引出概念（基本线段和组合线段），做好铺垫。

师：在数线段时，要按顺序才会不遗漏，为了表述的简单明确，我们把相邻两端点的线段称为“基本线段”（课件出示“基本线段”），把由这样2条或多条基本线段组合在一起的线段称为“组合线段”（课件出示“组合线段”），所以这里就是2条基本线段和1条组合线段，一共就是3条线段。（边说边在黑板上画并演示其中的基本线段和组合线段）写出算式：2+1=3（条）。

二、巧数线段的方法

师：大家在草稿纸上可以写写画画，数数看一共能数出几条线段？（2分钟后同桌交流）

（教师挑选学生不同的方法投影展示）

预设一：作图法（连一连）。可能有的是连的比较混乱，有的连的比较有序，注意让学生在黑板前演示连的整个过程。（让学生体会有序思考，为后面的探索做铺垫）

预设二：写算式（3+2+1=6）让学生说出算式中的每个数字所表示的意思，并演示出来，体会有序思考。

2.教师小结，理清思路。

师：我们知道，我们要数的线段包括了基本线段和组合线段，这里的基本线段有几条？（边说边演示并写出3）

师：2条合在一起的又有几条？（按顺序前两条组合到一起，后面两条组合到一起，黑板上演示一共2条）

师：3条合在一起的又有几条？

预设：1条。

师：算式是：3+2+1=6（条）。

3.出示：

一共有多少条线段？

（1）先独立数一数，写一写，画一画，再和同桌交流方法。

（2）汇报：

师：怎么列式？

生：4+3+2+1=10（条）

师：4表示什么？3表示什么？2表示什么？1呢？

预设：4表示基本线段一共4条，3表示2条基本线段组成的组合线段共3条，2表示3条基本线段组成的组合线段共2条······

【设计意图：先让学生独立完成，经过思考——验证——交流——汇报后，学生自由表达出自己的想法，教师在旁稍加引导，让学生于无形中体会和感悟有序思考的过程，最后总结出方法。】

4.回顾整理，总结方法。

（1）出示图和算式。

请同学们仔细观察这些线段和相对应的算式，说说巧数线段的方法。

教师引导学生观察：每个算式的第一个加数表示什么？第二个加数表示······

师：要数线段的总条数，应该先数什么？再怎么样？

预设：先数出基本线段的条数，再依次往后加直到加到1算出结果就可以了。

师：如果有100条基本线段，应该怎样算出线段的总条数？

生 ：100+99+98+97+ ……+1，算出结果就可以了。

（2）填表（建立基本线段的条数与端点个数的联系，进一步升华方法）

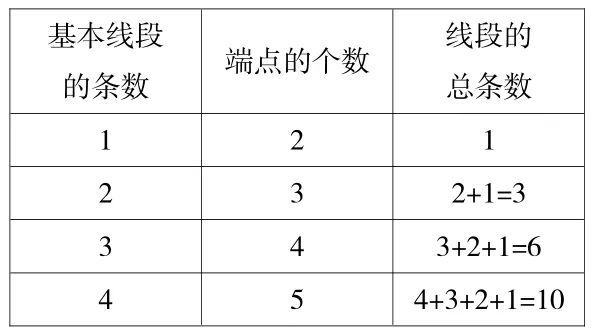
基本线段的条数 端点的个数 线段的总条数1 2 1 2 3 2+1=3 3 3+2+1=6 4 5 4+3+2+1=10 4

师：请同学们仔细观察这些线段的基本线段和端点的个数，你发现了什么？

生：端点个数比基本线段的条数多1。

师：一条线段中共有10个端点，基本线段有几条？20个端点呢？100个呢？

出示选择题：

1.如果一条线段中共有8个端点，要求线段总条数正确列式是（ ）。

2.如果一条线段中共有8条基本线段，线段总条数正确列式是（）。

A.9+8+7+6+5+4+3+2+1

B.8+7+6+5+4+3+2+1

C.7+6+5+4+3+2+1

【设计意图：进一步建立端点和基本线段之间的联系，用表格的形式回忆和总结数线段的整个过程，进一步夯实基础，理清思路。】

三、研究数角的方法

师：刚才我们总结出数一条组合线段中共能数出几条线段的巧妙方法，下面我们看从一个点出发引出两条线组成了一个什么？（角）

1.出示2个基本角组成的组合角。

师：图中一共有几个角？请你数一数，画一画，写一写。

（独立思考，同桌交流）

（请学生上台在投影中或黑板上展示数的过程及算式中每个加数表示的意义）

师：刚才数线段时我们要先数基本线段，这里数角我们也可以先数？

预设：基本角。

师：几个？（2个）组合角几个？（1个）一共就是：2+1=3（个）。

2.出示由4个基本角组合而成的角，这里共有几个角？怎么列式？

预设：4+3+2+1

师：（追问）4表示？3表示？2呢？1呢？

师：数角和数线段有什么相同点，谁来说说？

预设：都是先数基本的，再数两个组合在一起的，三个组合在一起的······

四、研究数三角形的方法（由线到面）

1.在4个基本角组成的图形的基础上加一条线段如图。（利用现有素材，巧妙延伸）

一共有（）条线段。

一共有（）个角。

一共有（）个三角形。

（教师引导学生数线段和角，建立数线段与数角，最后到数三角形之间的联系）

（学生独立完成，交流汇报方法，让学生说出基本角、组合角的概念）

2.变式训练1。

师：在上图的中间加上一横，这时一共有几个三角形？如何列式？

（独立思考再交流，请学生汇报）

预设：加一横就成了两层，所以要在原来的基础上乘2。

师：再加一横呢？再继续加呢？

预设：有几层就乘几。

3.变式训练2。

出示由5个相同长方形连在一起组合而成的图形。

一共有多少个长方形？如何列式？

【设计意图：通过两次变式训练，进一步拓开学生的思路，无形中从点、线、面中升华知识间的联系，使学生体会和养成有序的思考习惯，进而巩固新知。】

五、课堂小结