船舶电力永磁同步推进电机空间电压矢量DTC

秦俊峰， 白洪芬， 颜泽锌， 齐运永

(1.钦州学院 海运学院，广西 钦州 535000; 2.大连海事大学 船船电气工程学院，辽宁 大连 116026)

电力推进船舶由推进电动机取代传统的柴油机来驱动螺旋桨转动，不仅具有良好的经济性、操纵性和安全性，而且噪声低、污染物排放少，具有广阔的应用前景。永磁同步电动机(Permanent Magnet Synchronous Motor，PMSM)具有体积小、效率高和可靠性好等优点，在电力推进船舶中得到广泛应用。[1]

船舶电力推进系统虽然比较复杂，但经过一定的设计简化之后，可保证简化系统的仿真结果与实际模型的结果十分接近[2]，因此对船舶电力推进系统进行的研究较多，其中推进电机的类型及其控制方式的选择是船舶电力推进的关键技术之一。目前电力推进船上采用的推进电机主要是直流电机、异步电机和同步电机等，而直接转矩控制(Direct Torque Control，DTC)和矢量控制(Vector Control，VC)是主要的电机控制策略。[3-7]很多文献[8]只是简要分析电力推进系统，重点对推进电机的性能进行分析，未考虑推进电机与螺旋桨负载的特性匹配；也有文献[9-10]侧重于螺旋桨负载的特性，对不同工况下螺旋桨的动态过程进行仿真研究，但未考虑船舶推进电机对螺旋桨负载的带动情况。

相较于矢量控制，直接转矩控制不仅可省去坐标变换，还能得到良好的转矩响应速度和较高的转矩控制精度，但采用Bang-Bang离散两点的滞环控制会产生较大的电流、磁链和转矩脉动，且低速性能不佳。[11]因此，考虑采用基于空间矢量调制(Space Vector Modulation，SVM)的直接转矩控制算法，通过控制逆变器的开关状态来控制电压矢量，实现对定子磁链幅值及相位的实时控制，最终达到直接控制电机转速的目的。该系统结构简单、响应速度快、系统鲁棒性强[12]，更适用于船舶这种需快速响应的大惯量运动系统。

本文在分析电力推进船舶系统基本结构及数学模型的基础上，讨论基于空间电压矢量的直接转矩控制策略的基本原理，通过仿真验证船舶的额定负载启动性能、转速转矩突变及低速性能，并通过试验验证所提出的直接转矩控制策略的正确性和可行性。

1 船舶电力推进系统PMSM数学模型

船舶电力推进系统由推进电动机、推进电机逆变器、船舶推进器、螺旋桨和控制装置等构成。[13]船舶运行时，推进电机直接驱动螺旋桨转动；螺旋桨转动时在水中产生向前的推力，通过桨轴和推力轴承等作用于船体，推动船舶运动。此外，海浪、海风等海洋环境的变化会使船舶阻力发生变化，进而引起螺旋桨负载转矩发生变化，最终导致推进电机的特性发生变化。[14]

由文献[15]得到船舶螺旋桨模型见图1。

在电力推进船舶中，由推进电机与螺旋桨的相互关系可知推进的动力方程[15]为

Jn=Qe-Qp-Qf

(1)

式(1)中：J为转动惯量；Qe为电磁转矩；Qf为摩擦转矩；Qp为推进转矩。由式(1)可知，船速主要由推进电机转速n决定。

2 船用永磁同步电机SVM-DTC控制基本原理

基于SVM的永磁同步电机直接转矩控制系统框图见图2。与传统的DTC相比，该系统添加有转矩PI调节器和参考电压矢量计算单元，采用SVM单元控制逆变器的工作，对电机参数的依赖度小，更便于调节控制。

2.1 SVM控制

电机的直接转矩控制系统是根据转矩误差、磁链误差及磁链位置来确定逆变器的开关信号的。本文选用电压型逆变器(见图3)，UDC为直流供电电压。

根据逆变器的工作原理，若设逆变器上桥臂导通时为状态“1”，下桥臂导通时为状态“0”，则三相逆变器的开关共有8种状态组合，所形成的电压矢量分布见图4。表1为定子磁链扇区划分与磁链空间角度θ的关系，角度θ由arctan(Ψsβ/Ψsα)决定。

与矢量控制相比，直接转矩控制无需确定转子的准确位置。根据电压矢量的控制位置将定子空间划分为6个扇区(如图4所示)，在进行实时控制时，仅确定定子磁链所处的扇区即可结合其他控制输入信号推算出合适的控制参考电压矢量，完成系统控制。参考电压可在αβ坐标系内生成。

表1 定子磁链扇区与磁链空间角度的关系

(2)

空间电压矢量调制SVM模块采用SVPWM技术，根据参考电压的值判断出参考电压矢量所在的扇区，由参考电压矢量所在扇区相邻的2个有效电压空间矢量和零电压矢量合成期望的参考电压空间矢量，替换传统的直接转矩控制中的电压矢量开关表，进而实现对转矩和磁链的控制，使电机内部形成圆形旋转磁场。

2.2 定子磁链

若忽略定子电阻压降的影响，定子合成电压与合成磁链的空间矢量关系[16]可近似表示为

(3)

式(3)中：Rs为定子电阻；us和is分别为合成定子电压矢量及电流矢量。由式(3)可知，电机定子磁链矢量与定子电压矢量存在近似的积分关系，在空间上定子磁链矢量超前定子电压矢量90°。

图5为参考电压空间矢量与磁链空间矢量的位置关系，其中：Ψs和Ψr分别为定子磁链及转子磁链；Ψsref为定子磁链的参考值，即定子磁链的给定值；δ为转矩角；θs和θr分别为定子磁链及转子磁链与α轴的夹角；ΔΨ和Δδ分别为参考电压矢量作用ΔT时间之后的定子磁链增量及转矩角增量；usref为参考电压。

由图5可知αβ坐标系下的定子磁链与参考磁链之间的相互关系为

(4)

结合转矩调节器控制，定子电压在α轴和β轴上的电压参考值可表示为

(5)

2.3 转矩计算

在仅考虑基波磁动势的情况下，PMSM的电磁转矩可表示为

(6)

3 系统仿真模型的建立及结果分析

为验证船机桨的性能匹配及基于SVM-DTC策略的可行性，在MATLAB/Simulink中搭建电力推进船舶仿真系统。电机的仿真参数见表2。

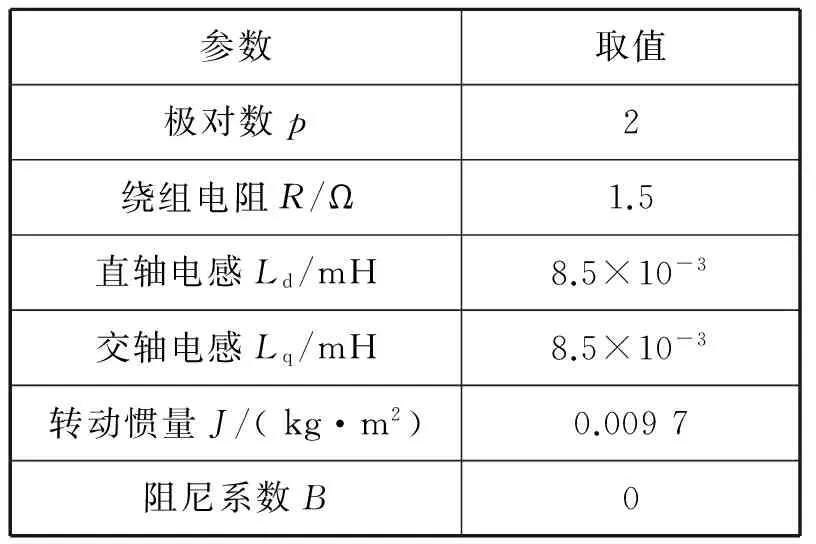
表2 电机的仿真参数

仿真时，滞环宽度取0.01，磁链初值设为1.5 Wb，SVM采样周期为T=0.000 1 s。

1)给定负载10 N·m启动，给定额定转速200 r/min，稳定运行；t=0.2 s时突减速至100 r/min；t=0.4 s时突加速至200 r/min；t=0.6 s时突反转至-200 r/min，仿真波形见图6。

带载启动时，电机从零转速上升到给定转速所需时间约为0.03 s；到达稳态之后，电磁转矩为给定负载10 N·m。在恒定负载下，转速突降和突增时

a)定子磁链圆轨迹b)电机转速c)电磁转矩d)定子三相电流

图6 带载启动及速度突变的仿真曲线

所需时间约为0.01 s，从转速发生反转到给定速度约需0.02 s；同时，电磁转矩和电流在经过短时间波动之后重新稳定于初始值，说明直接转矩控制具有很强的动态响应能力。

2)低速性能仿真，给定转速n=100 r/min启动，稳定运行至0.2 s突然减速至60 r/min；t=0.4 s时突然减速至40 r/min；t=0.6 s时突然减速至20 r/min。相应的仿真波形见图7。

a)定子磁链圆轨迹b)电机转速c)电磁转矩d)定子三相电流

图7 低速的仿真曲线

由图7可知，该系统具有良好的低速运转性能，且响应速度很快。

4 试验验证

为进一步验证提出的SVM-DTC控制策略的正确性，利用实验室永磁同步电机，通过DSP编程，模拟电机直接转矩控制。图8为试验用三相永磁同步电机及硬件控制电路，其中：永磁同步电机的参数与表2中的参数相同；控制电路包括电流及电压检测电路和驱动电路。

在试验中，电机转速给定为200 r/min，磁链给定值为0.6 Wb，给定转矩为0.25 N·m。采用基于空间电压矢量的直接转矩控制策略，所得试验结果见图9。

由图9a)可知：电流波形具有良好的正弦度，符合直接转矩控制的要求。由图9b)可知：实际转速能达到给定转速200 r/min；由于试验过程中会受到硬件电路、环境等因素的影响，因此实际转速会有一定的波动；转速脉动约为10%，能一直跟踪给定转速，因此该控制策略是正确可行的。由图9c)可知：磁链幅值一直维持在给定值0.6 Wb附近，磁链幅值脉动约为4.2%，完全符合DTC对定子磁链幅值控制的要求。由图9d)可知：电机的输出转矩基本在0.25 N·m附近波动，转矩脉动约为150%，与直接转矩控制理论相符。由试验测得的波形可知，基于空间电压矢量的直接转矩控制策略能很好地控制电机运行，转矩脉动、磁链脉动均可控制在理论值范围内。

b)电流及电压检测电路c)驱动电路

图8 永磁同步电机控制系统试验平台

图9 试验波形

5 结束语

本文在分析船舶电力永磁同步推进电机数学模型的基础上，对基于空间矢量调制的直接转矩控制算法进行分析。通过仿真， 对基于SVM的直接转矩控制策略进行验证。仿真结果表明：船用永磁同步推进电机动态转矩的响应时间很短，推进电机的响应速度快且平稳，在很短的时间内便能稳定达到给定转速，在转速和转矩突变的情况下仍能快速响应，系统具有良好的动态响应能力和抗干扰能力。通过试验波形可进一步验证所提直接转矩控制策略的正确性。因此，基于SVM的直接转矩控制算法适用于船舶电力推进系统，能满足对船用大功率永磁同步电机推进系统动态响应时间的要求。

[1] 白洪芬，朱景伟，秦俊峰. 改进滑模观测器在船舶电力推进 PMSM 无位置控制中的应用[J].中国航海，2015,38(4):22-25.

[2] 杨明国.全电力船舶的电力推进系统建模与仿真[J].船电技术，2014, 34(10):19-22.

[3] 郑仁求，俞万能，陈景峰．太阳能游览船舶电力推进系统仿真[J]．集美大学学报(自然科学版)，2014，19(2)：122-126．

[4] 郭昊昊，刘彦呈，任俊杰.电力推进船舶中永磁电机直接转矩控制[J].电机与控制应用，2011,38(11):30-33.

[5] 李彦，唐智星. 基于三电平SVM技术的船舶电力推进DTC研究[J].舰船科学技术,2013,35(12):32-36.

[6] 申喜，唐颖，魏文轩，等.基于Simulink的船舶电力系统的仿真[J].舰船电子工程，2013,33(9):91-95.

[7] 马静怡，魏海峰，刘维亭.船舶电力推进PMSM DTC的空间电压矢量选择研究[J].中外船舶科技，2014(3):25-27.

[8] 李彦，唐智星.船舶电力推进DTC系统低速性能的改善研究[J].科学技术与工程,2013,13(7):1773-1778.

[9] 马继先，陈源，陆振伟.船舶电力推进系统螺旋桨负载的建模与仿真[J].电子设计工程，2014,22(1):56-59.

[10] 秦业志，阮礽忠. 吊舱式电力推进船舶螺旋桨匹配设计仿真研究[J].中国舰船研究，2014，9(6):65-72.

[11] 池飞飞. 船用永磁同步电机直接转矩控制仿真研究[D].武汉：武汉理工大学，2013.

[12] 曹林柏，赵宏革，张智远，等.基于十二电压矢量的电力推进PMSM直接转矩控制仿真[J].大连海事大学学报，2015,41(1):100-103.

[13] 沈爱弟，褚建新，康伟．内河船舶电力推进系统设计[J]．上海海事大学学报，2009，30(2):20-24．

[14] 李中兵，张欢仁．基于扩展卡尔曼滤波的船舶电力推进系统仿真[J]．中国航海，2011，34(4):45-50．

[15] 池波，翁爽. 船舶电力推进系统建模与仿真研究[J].船电技术，2014,34(9):76-78.

[16] 赵亮.电力推进船舶PMSM直接转矩控制系统的研究[D].大连：大连海事大学，2010.