基于首次穿越理论的船舶搁浅风险计算

赵江艳， 刘 文， 张明阳， 徐强强， 谢 平,4

(1. 武汉大学 水资源与水电工程科学国家重点实验室，武汉 430072； 2. 武汉理工大学 内河航运技术湖北省重点实验室，武汉 430063； 3.国家水运安全工程技术研究中心，武汉 430063； 4. 国家领土主权与海洋权益协同创新中心，武汉 430072)

长江属于季节性大型河流，受季节性因素和通航枢纽下泄流量等因素影响，航道水位变化明显，尤其是长江中游航道，年最高水位与年最低水位的多年平均值之差高达13 m，对船舶通航安全的影响显著。[1]通过对长江航道的事故进行统计分析发现，2013年和2014年枯水期发生的水上事故均占当年事故总数的50%以上，其中长江中游航道是长江干线的碍航瓶颈，有近20处碍航浅滩及10多个重点浅水道，通航条件十分不稳定，极易发生搁浅事故，从而造成碍航局面。[2]因此，对水位变化下的长江中游船舶搁浅风险进行分析具有实际应用价值。

船舶搁浅风险分析已在水上交通工程领域引起广泛关注，但不同通航环境下的船舶搁浅风险的定量计算依然是亟待解决的问题。通常采用的研究方法有故障树方法、贝叶斯方法及概率模型等。[2-8]AMROZOWIEZ[6]将船舶搁浅事故分为动力性搁浅和漂移性搁浅，分别建立故障树，确定失效概率；KITE-POWELL等[7]根据统计学中的贝叶斯方法提出船舶搁浅的风险计算模型，可有效预测船舶搁浅风险，定量计算相应的直接经济损失和间接经济损失；ARSHAM等[8]利用船舶交通和航道复杂度建立评估船舶搁浅概率的模型等。从以上研究成果中可看出，大多数研究是从整体的角度或从船舶的搁浅现象出发，阐述有关船舶搁浅分析的总体看法。但是，船舶搁浅分析中的影响因素与研究区域的交通条件、自然条件紧密相关，因此无法推广到所有地区。此外，由于交通环境和自然环境会随时间变化，因此船舶的搁浅分析应是一个适应新的风险因子的动态过程。对此，本文将船舶搁浅问题视为首次穿越问题，根据随机振动的首次穿越失效理论建立首次穿越失效(船舶搁浅)模型。首次穿越问题是指一个受随机参激或随机外激作用的动力学系统，其响应在相空间上发生随机扩散。当系统响应第一次离开某个安全域或允许域时，就称系统发生首次穿越。首次穿越在工程[9]、物理[10]、生物[11]、医学[12]及经济[13]等学科中广泛存在。QUY等[14]将首次穿越理论引入到船舶搁浅的概率模型中，初步验证该理论在解决船舶搁浅问题上的适用性，但在具体的建模过程中仅考虑航速变化对船舶吃水的影响，没有解决航道水位变化对船舶搁浅风险影响的问题。

对此，本文重点研究长江中游航道水位变化对船舶通航安全的影响。为保证分析结果的可靠性，运用随机振动的首次穿越失效理论构建船舶搁浅概率计算模型，定量分析不同水位下船舶的搁浅概率；同时，给出船舶搁浅概率分别为0和1时对应的水位临界值，用以验证实际的设计最低通航水位是否符合通航安全的要求。

1 问题描述与建模

船舶搁浅事故是一种受多种因素影响的水上交通事故，在分析船舶搁浅风险的影响要素时，除了不同时期的水位变化之外，人为因素、船舶因素等不受水位变化影响的因子也会对船舶的搁浅风险造成一定的影响。若进行全面考虑，则会增加求解问题的难度，甚至无法求解。因此，本文在船舶搁浅风险的分析中主要考虑水位变化对船舶搁浅的影响，参考波浪载荷下船舶运动响应研究中的谱分析方法的基本思路分析船舶的垂向运动，基于首次穿越理论构建船舶搁浅风险计算模型。

1.1 水位变化对船舶搁浅的影响

搁浅事故表明，航道水深不足是导致船舶发生搁浅的直接原因。[15]由于航道深度在一定时期内是不变的，因此航道水位的变化也可间接描述航道水深的变化，从而建立水位与船舶搁浅风险之间的关系。富余水深、航道水深及船舶吃水之间的关系见图1，其中：H为航道水深；W为当时当地实际水位；d为图示水深；D为船舶吃水；Δh为富余水深。富余水深主要包括船舶航行下沉量和触底安全富余量2部分，其主要作用是防止船舶触底，保证船舶安全航行。有关系式

H=W+d

(1)

允许船舶的最大吃水

Dmax=H-Δh=W+d-Δh

(2)

一般而言，增大富余水深Δh的取值会提高船舶的通航安全，同时会降低航道的通航能力。因此，为平衡通航安全与通航能力之间的关系，须对富余水深Δh进行合理取值。《内河通航标准》[16]根据航道等级规定了相应的富余水深。

由式(2)可计算任意水位下允许船舶的最大吃水，当实际吃水大于该最大吃水时，船舶发生搁浅。由生产实践可知，即使船舶的载货量一定，船舶的吃水也会随着通航环境的变化而变化。这是因为船舶航行时不仅会受波浪的影响产生升沉运动的响应位移，还会受周围水流的影响出现下沉现象。船舶航行下沉量(即船舶动吃水)是指船舶航行中的吃水较静止时的增加量，本文采用实际航运中推荐的公式，即

(3)

式(3)中：CB为方形系数；v为船速，kn。

因此，计算船舶搁浅概率的前提是确定当时当地的水位及船舶的动态吃水。对于载货量一定的单艘次船舶来说，水位越高，船舶的搁浅风险越小。

1.2 水位变化下船舶搁浅风险计算模型

1.2.1建模的基本假设

为避免模型自身的复杂性带来不确定性风险，参考波浪载荷下船舶运动响应研究的谱分析方法[17-20]，确定建模的2个基本假设：

(1)波浪表面是一个各态历经的零均值高斯随机过程；

(2)船舶为一个线性系统。

假设(1)与随机波浪理论的思想一致，认为在任意较短的时间内，波浪符合零均值的平稳正态随机过程，其统计特性[21-23]可用功率谱密度来确定，即

(4)

式(4)中：S(ωi)为波浪功率谱密度函数，表示一个随机波浪所包含的所有频率及其对应的能量。

在波浪载荷的作用下，船舶会产生位移、切力、弯矩及应力等各种响应。[24]若将波浪的作用记为Q(t)，则有

(5)

式(5)中：mQ为Q(t)的均值；An和Bn为互不相关的随机变量。An和Bn有均值为零、方差相等的特征，即mAn=mBn=0，DAn=DBn=Dn。

波浪的方差为

(6)

(7)

因此，当Δω→0时，可得

(8)

式(7)和式(8)中：SQ(ω)为波浪谱。

对于单自由度系统，假定受一简谐干扰力作用，则振动方程为

(9)

式(9)中：q(t)为广义位移；ω0为系统固有频率；ξ为黏性阻尼系数；Q0为干扰力幅值；ω为干扰力频率。

该系统的响应为

q(t)=q0eiωt=H(ω)Q0eiωt=H(ω)Q(t)

(10)

根据假设(2)，将垂向运动的船舶视为单自由度的线性系统，将波浪作为系统的输入量，则船舶垂向运动的响应即为系统的一种输出，其值由波浪载荷和响应函数共同决定。响应函数的物理意义是各种不同频率的单位波幅余弦波产生的船舶响应。若定义H(ω)的模|H(ω)|为响应函数，则有

|H(ω)|=q/Q0

(11)

利用傅里叶变换可知

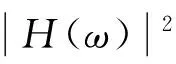
(12)

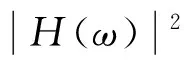
因此，作为船体—波浪线性系统的随机输出，波浪载荷在短时间内也服从零均值正态分布，其幅值遵循Rayleigh分布特性。[25-26]

1.2.2船舶垂向运动建模

建立坐标系O-xyz见图2，当将船体作为刚体看待时，船舶的摇荡运动是沿3个坐标轴方向的位移和转动，具有6个自由度。在不考虑舵力作用的情况下，船舶的六自由度运动可分解为纵向和横向2组耦合运动，其中：纵向运动由升沉、纵摇和纵荡组成；横向运动由横荡、横摇和艏摇组成。

纵向耦合运动与横向耦合运动之间的影响很小，且自由状态下船舶的纵荡运动对船舶升沉运动位移的分析影响不大。因此，在求解船舶在波浪中的升沉运动位移时，不用考虑船舶的纵荡运动，只需研究船舶升沉和纵摇的耦合运动。

船舶升沉和纵摇的耦合运动的微分方程为

(13)

(14)

(15)

式(15)中：

水动力系数可通过计算近似得到。由此可得

(16)

式(16)中：Az=E-1M；Bz=E-1N；随机波浪W为有色噪声。

若选择船舶升沉运动的位移和纵摇倾角为测量状态，则测量方程为

Y=CzX+V

(17)

本文利用波浪扰动成形滤波器计算船舶受到的波浪干扰，其核心思想是将高斯分布的白噪声通过一个波浪扰动成形滤波器G(s)，从而得到作为随机波浪扰动仿真过程的有色噪声。[17]若将成形滤波器视为船舶运动系统的一部分，则可将白噪声信号视为新系统的扰动。新系统的组成见图3。

图3中：GZ(s)为波浪对船舶纵向扰动力的成形滤波器；GM(s)为波浪对船舶纵向扰动力矩的成形滤波器。通常选取成形滤波器

(18)

式(18)中：s为Laplace算子；G0为增益；ω0为中心频率；ξ为阻尼系数。wZ(t)和wM(t)均为白噪声信号，其均值为0，方差为1；Z(t)为船舶升沉运动干扰力；M(t)为纵摇干扰力矩；q(t)为最终求得的船舶垂向响应位移。

因此，当波浪的白噪声信号wZ(t)和wM(t)已知时，可通过上述成形滤波器得到船舶升沉运动干扰力Z(t)和纵摇干扰力矩M(t)，随后结合船舶运动的状态方程求出船舶垂向运动响应位移q(t)。

可运用Simulink工具箱对上述新系统进行仿真，从而得到船舶垂向运动响应位移q(t)。仿真流程图见图4。

1.2.3船舶搁浅风险量化建模

由“1.2.1”节可知，船舶在波浪激励下产生响应，由于激励是服从高斯分布的，运动响应是线性的，最后得到的船舶运动也符合高斯分布。因此，若运用船舶搁浅的数学关系式D>H，即船舶吃水大于航道水深，则船舶搁浅问题可看成首次穿越失效问题：将航道水深表示成随时间变化的阈值，当船舶垂向的位移响应首次穿越该阈值时，认为船舶发生搁浅。首次穿越概率(即船舶的搁浅概率)可通过相关的随机理论计算得到。

通过分析可知，船舶在时域内穿越的失效阈值可表示为

φ(t)=W(t)+h-D

(19)

式(19)中：W为当时当地实际水位；h为航道图示水深；D为船舶吃水。

图5为船舶搁浅(首次穿越失效)示意，若在船舶航行期间(即[0，T]内)，其升沉运动响应位移q(t)穿过φ(t)，则船舶首次穿越失败，即发生搁浅事故。

令β=φ(t)，则船舶响应的期望穿阈率[27]可表示为

(20)

式(20)中：m0和m2分别为船舶运动响应谱的零阶矩及二阶矩。m0和m2的计算式可表示为

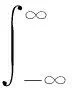
(21)

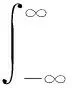
(22)

式(21)和式(22)中：Sq(ω)为描述在频率域ω上响应x(t)的均值分布的功率谱密度函数，即船舶运动响应谱。船舶运动的响应谱实质上是一个功率谱密度函数，描述信号功率随频率的分布状况。

根据“1.2.2”节可求出船舶垂向运动的响应位移q(t)。将q(t)视为一个随时间变化的随机信号。以Ts对随机信号进行等间隔抽样，得到随机序列q(nTs)，记为X(n)；随后通过直接法、间接法、Bartlett法或Welch法计算得到其谱密度函数。

若应用首次穿越理论，则船舶首次穿越失效的概率(即船舶的搁浅概率)可表示为

P(β|T)=1-exp(-vβT)

(23)

2 实例计算与结果分析

选取一艘满载排水量为2 858 t的船舶作为研究对象，运用本文提出的方法计算其搁浅风险。该船的具体参数为：船长75 m；垂线间长71.33 m；型宽13.4 m；型深5.4 m；设计吃水4.2 m；方形系数0.704；水线面系数0.980；中横剖面系数0.980；满载排水量2 858 t。

根据水文和气象条件，将内河船舶航行区域划分为A，B，C等3级(见表1)。长江中游主要属于B级航区，根据该航区的波浪要素及船舶尺度确定

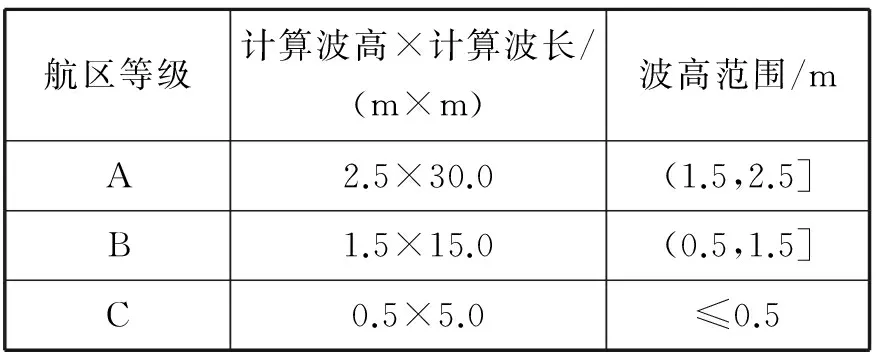
表1 我国内河各级航区波浪要素

波浪成形滤波器的参数见表2。

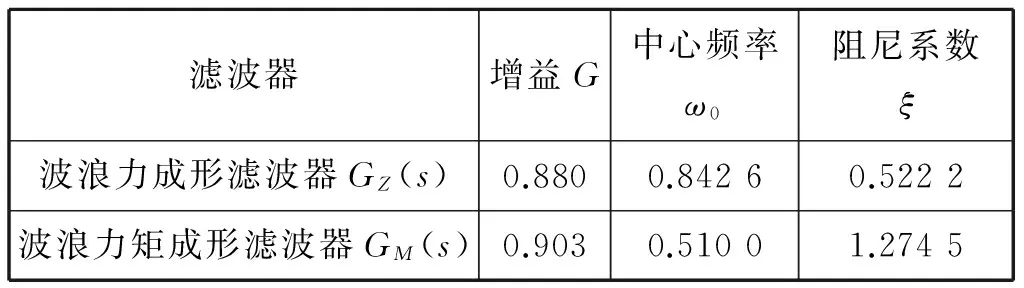
表2 波浪成形滤波器的参数

将上述船舶尺度、图示水深(3.2 m)及船舶与波浪的遭遇频率(π/5)等数据作为输入，结合MATLAB/Simulink仿真平台(如图4所示)，便可求出波浪干扰力、波浪干扰力矩及船舶升沉运动的响应位移。设定仿真时间为60 s，波浪对船舶升沉运动的干扰力和干扰力矩分别见图6及图7。从图6和图7中可看出：船舶受到的波浪载荷符合正态分布，其幅值符合Rayleigh分布。因此，当将船舶视为一个线性系统时，船舶的运动响应过程是各态历经的平稳随机过程，运动幅值也符合Rayleigh分布(见图8)。

运用基于MATLAB的谱估计程序实现船舶升沉运动响应位移到船舶响应谱的转化，最终得到船舶升沉运动的响应谱见图9。随后运用首次穿越理论计算得到船舶搁浅概率与水位的关系见图10。

从图10中可看出：随着航道水位下降，船舶搁

浅风险逐渐增大；随着航道水位升高，船舶搁浅风险逐渐减小。船速越大，船舶搁浅概率为0对应的水位临界值越大；船速越小，船舶搁浅概率为0对应的水位临界值越小。具体临界值见表3。

表3 不同船速v下的水位临界值

通过分析可知：船速越大，船舶的运动响应越显著，船舶升沉运动的响应幅值越大；同时，船速越大，船舶航行下沉量越大，故其对通航水位的要求越高。因此，利用上述方法不仅可确定某一水位下船舶的搁浅概率，还能由船舶搁浅风险的容忍度确定航道的最低通航水位，从而验证实际的设计最低通航水位是否符合要求。

此外，由于当时当地的实际水位与图示水深之和即为航道水深，故该方法也可为航道部门确定航道维护水深提供一定的参考。

3 结束语

本文提出一种基于首次穿越失效理论的船舶搁浅风险的定量计算方法，建立水位变化下的首次穿越失效(船舶搁浅)模型。同时，以长江中游航道的典型船舶为例，定量计算其在浅水航段的搁浅风险，最终得到船舶搁浅概率与航道水位的对应关系。从结果上看：在同一船速下，航道水位越低，船舶的搁浅风险越大；船速越大，船舶搁浅概率为0和1对应的水位临界值越大，与实际情况一致。研究结果表明，该方法不仅能确定某一水位下船舶的搁浅概率，还可确定船舶搁浅概率为0和1时对应的水位临界值。此外，利用该方法还能求得任一可接受搁浅概率下的最低水位值。因此，该方法可用于确定船舶搁浅风险容忍度下的最低通航水位，为最低通航水位的设计提供新的思路，为航道部门确定航道维护水深和航运经营人对船舶进行配载提供参考。

[1] 刘婷.水位变化对长江中游航运物流成本的影响机理及模型研究[D]. 武汉: 武汉理工大学, 2014.

[2] 张笛. 枯水期长江通航风险评价和预测方法研究[D]. 武汉: 武汉理工大学, 2011.

[3] 陈婷婷, 施朝健, 雷琴. 船舶搁浅模糊故障树的灰色模糊关联分析[J]. 中国航海, 2015, 38(3):83-88.

[4] 吴金龙, 刘大刚, 范中洲,等. 大风浪条件下渤海海区重点船舶风险评估模型[J]. 中国航海, 2012, 35(2):89-92.

[5] MAZAHERI A, MONTEWKA J, KUJALA P. Modeling the Risk of Ship Grounding—A Literature Review from a Risk Management Perspective[J]. WMU Journal of Maritime Affairs, 2014, 13(2): 269-297.

[6] AMROZOWIEZ M D. The Need for a Probabilistic Risk Assessment of the Oil Tanker Industry and a Qualitative Assessment of Oil Tanker Groundings[Z]. Massachusetts Institute of Technology, 1996.

[7] KITE-POWELL H L, JIN D L, JEBSEN J L, et al. Investigation of Potential Risk Factors For Groundings of Commercial Vessels In U S Ports[J]. International Journal of Offshore & Polar Engineering, 1999, 9(1)：16-21.

[8] ARSHAM M, JAKUB M, PENTTI K, et al. Assessing Grounding Frequency Using Ship Traffic and Waterway Complexity[J]. Journal of Navigation, 2015, 68(1):89-106.

[9] ZHANG L Y, SUN L M, SHANG Z Q. Real-Time Reliability Assessment Based on Acceleration Monitoring for Bridge[J]. Science China Technological Sciences, 2016,56(8): 1-11.

[10] SHARMA K, KUMAR N. First-Passage Time: Lattice Versus Continuum[J]. Physical Review E, 2012, 86(3): 032104.

[11] HU Z, CHENG L, BERNE B J. First-Passage Time Distribution in Stochastic Processes with Moving and Static Absorbing Boundaries with Application to Biological Rupture Experiments[J]. Journal of Chemical Physics, 2010, 133(3): 034105.

[12] SIROVICH L, KNIGHT B. Spiking Neurons and the First Passage Problem[J]. Neural Computation, 2011, 23(7): 1675-1703.

[13] BAKSHI G, PANAYOTOV G. First-Passage Probability, Jump Models, and Intra-Horizon Risk[J]. Journal of Financial Economics, 2010, 95(1): 20-40.

[14] QUY N M, VRIJLING J K, GELDER P, et al. On the Assessment of Ship Grounding Risk in Restricted Channels [C]. 8th International Conference on Marine Sciences and Technologies, 2006: 294-299.

[15] 任亚磊, 牟军敏, 李亚军, 等. 进港航道中船舶搁浅概率的蒙特卡洛仿真[J]. 船舶力学, 2014, 18(5): 532-539.

[16] 交通运输部.内河通航标准：GB 50139—2014[S]. 北京: 中国计划出版社, 2014.

[17] 彭秀艳, 张文颖, 何志勇. 基于谱估计方法的船舶纵向运动建模预报研究[J]. 自动化技术与应用, 2008, 27(11): 1-4.

[18] DINIS M S, PIERSON J W J. On the Motion of Ships in Confused Seas[Z]. Routledge, 1953,22(23):8144-8154.

[19] 李成成. 船舶在波浪中运动时域数值模拟研究[D]. 上海：上海交通大学, 2010.

[20] 杭栋栋. 基于船舶运动响应数据的海浪估计方法研究[D]. 哈尔滨：哈尔滨工程大学, 2013.

[21] 徐德伦, 于定勇. 随机海浪理论[M]. 北京：高等教育出版社, 2001:111-115.

[22] 俞聿修. 随机波浪及其工程应用[M]. 大连: 大连理工大学出版社, 2011:60-81.

[23] KIMURA A. Statistical Properties of Random Wave Groups[Z]Coastal Engineering,1980:2955-2973.

[24] 王学亮. 大型起重船在海浪中的运动响应研究[D]. 天津: 天津大学, 2003.

[25] 吴小平. 基于切片理论的波浪载荷直接计算[J]. 船舶与海洋工程, 2010(4):21-25.

[26] PEREZ T, BLANKE M. Ship Roll Damping Control[J]. Annual Reviews in Control, 2012, 36(1):129-147.

[27] QUY N M, VRIJLING J K, VAN GELDER P. Risk-and Simulation-Based Optimization of Channel Depths: Entrance Channel of Cam Pha Coal Port [J]. Simulation, 2008, 84(1): 41-45.