六相无刷直流电机分数阶PIλ控制的分析与仿真

彭晟楠，刘小兵，龙 驹

(西华大学，成都 610039)

六相无刷直流电机分数阶PIλ控制的分析与仿真

彭晟楠，刘小兵，龙 驹

(西华大学，成都 610039)

建立分数阶PIλ的逼近公式，在MATLAB/Simulink的环境下，搭建分数阶PIλ和普通PI转速控制系统的六相无刷直流电机仿真模型。结果表明,相比于普通PI控制，当分数阶PIλ控制在阶次值为0.5～0.9的范围内时，不仅能够更加快速、精准地跟踪给定速度 ,并且对负载扰动及参数变化具备更好的抗扰能力和稳定性。通过分析对比不同阶次下电机的波形，确定出0.5～0.9之间PIλ控制器的最佳阶次值为0.8。

分数阶PIλ控制；六相无刷直流电机；MATLAB

0 引 言

相对于有刷电机，无刷直流电机具有体积小、质量轻、维护方便、调速性能好、运行效率高等优点，应用于多个领域[1]。国内外目前无刷直流电机的研究还是三相居多，在多相电机的研究中大多以五、六相电机为基础[2]。为了使无刷电机调速系统得到提升，近年来，众多学者进行了深入研究。常用的方法有基于DPS的控制，无位置传感器控制与模糊PI控制等。DPS的运算速度比较高，可实现复杂算法的实时控制[3],使无刷电机实现数字化，但是只是在经典PID算法上稍作修改，并没有使用更好的算法[4]；无刷电机在没有位置传感器的情况下能够成功换相，电机能够稳定运行，调速平滑,但是其稳定性和抗干扰能力需要进一步提升[5]。用模糊PID控制方法控制无刷直流电机, 能够实现响应速度快、无超调、控制精度高且系统对干扰和参数变化具有较强的鲁棒性[6]，但在六相上的研究却很少。

针对以上问题，本文提出了的六相无刷直流电机分数阶PIλ控制。根据六相无刷直流电机的数学模型[7]，在MATLAB/Simulink软件环境下，通过搭建分数阶PIλ控制器和普通PI控制器的基本模型，利用仿真波形对比两者优缺点[8]，分析分数阶PIλ控制器的无刷直流电机达到稳定时间的长短以及超调量的大小，这为改善无刷电机动调速系统性能的研究提供了可靠依据。最后分析不同阶次下电机的波形，确定出0.5～0.9之间PIλ控制器的最佳阶次值。

1 分数阶转速控制器设计

1.1分数阶微积分定义

分数阶微积分现在有3种定义方式[9]，分别是GL(Grunwald-Letnikov)，RL(Riemann-Liouville)，Caputo。本次设计采用GL方式定义。分数阶微积分[10]定义如下：

式中:α和t是表达式的上下限;λ是表达式的阶次，Re(λ)是λ的实数部分。本文中λ只为实数。

1.2分数阶转速PIλDμ控制器设计

1.2.1设计理论

分数阶PIλDμ表达式：

式中：e(t)为误差变量;KP为比例参数;Ki为积分参数;Kd为微分参数;λ为积分阶次;μ为微分阶次。通过5个参数的合理设置，可以减小波形的超调量、提高控制精度，使系统更快达到稳定。

分数阶PIλ与参数的关系，如图1所示。

从图1可知，当λ=μ=1时，分数阶PIλDμ的参数设置范围表示它所围成的面积，分数阶控制器数学模型就变成了传统的整数阶控制器。当然λ和μ选择的值是不一定的，可以根据自己的需求或者其他原因选择合适的参数。

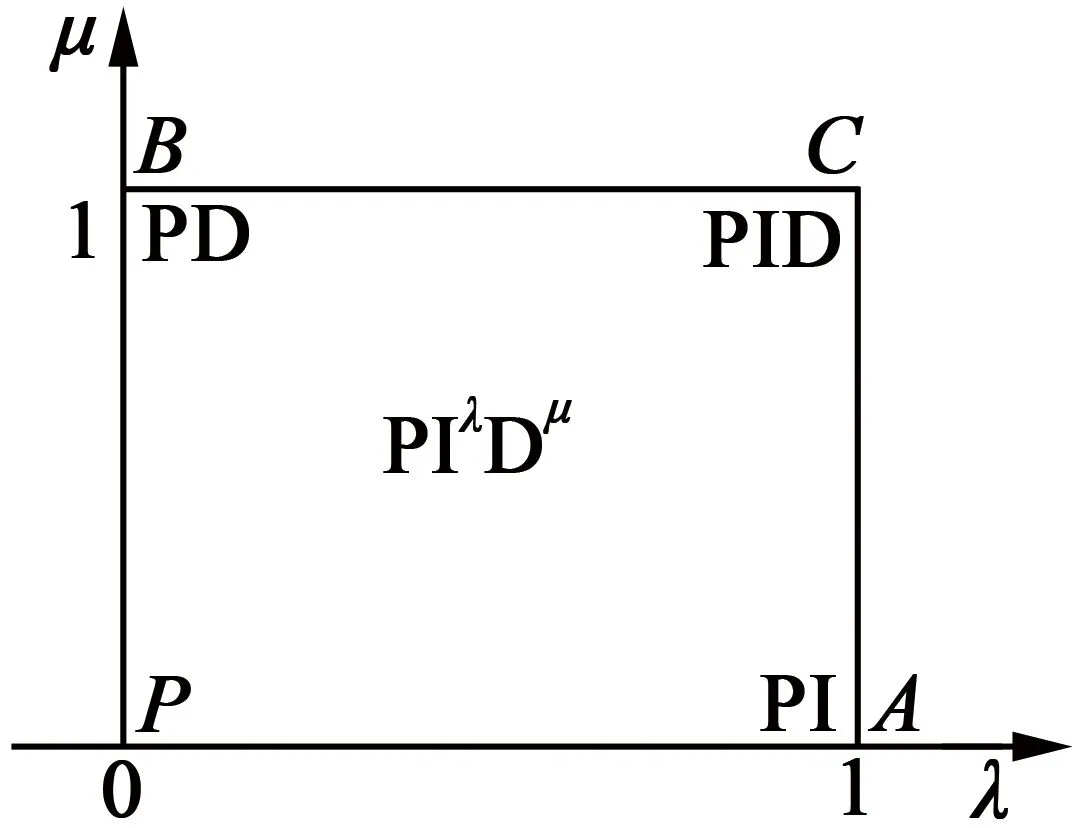
图1 控制器与参数的关系

1.2.2分数阶PIλ的逼近原理及表达式

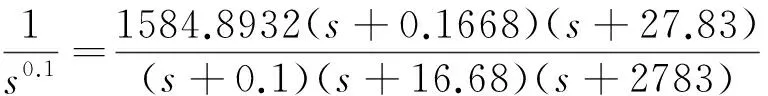
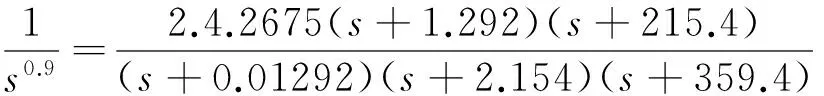
2 系统仿真

2.1电机模型与参数

2.1.1六相无刷直流电机总体仿真模型

仿真框图如图2所示。

因为六相无刷直流电机互感不仅存在于同一套绕组之间，也存在于两个绕组之间。这使得六相无刷直流电机的本体模块复杂性增加了许多。表1为六相无刷电机的参数。

图2 六相无刷直流电机整体仿真模型框图

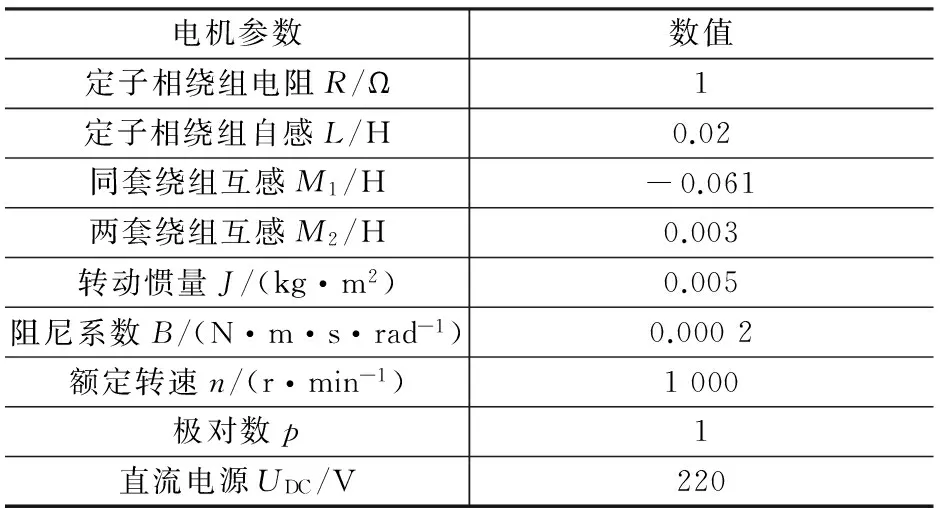
表1 六相无刷直流电机的参数

2.1.2分数阶转速PIλ控制器仿真模型

由于所设计出来的微积分模块是非线性的，所以直接求出它的值是非常困难的。于是可以利用Simulink中的Oustaloup滤波器来求解[12]。模块的构造如图3、图4所示。

图3 微积分模块

图4 封装模块

我们把普通PI转速环节中积分环节替换成分数阶PIλ的微积分模块。分别将图3中的各个逼近公式输入到上面的分数阶转速PIλ控制器中，在相同的条件下比较转速和转矩的波形。

2.2 系统仿真结果与分析

在MATLAB/Simulink软件环境下，对电机内部的速度仿真模块加装分数阶PIλ智能控制系统对无刷直流电机系统进行仿真，并对该系统的仿真结果与普通PIλ进行对比与分析。最后寻求0.1～0.9范围内，分数阶PIλ控制器阶数λ的最佳值。

本设计将分别在空载、负载和去载3种情况下进行仿真，并仔细比较转速，转矩等电机关键参数的波形。

2.2.1 六相电机普通PI与分数阶PIλ对比分析

我们通过仿真比较六相无刷电机普通PI控制与分数阶PIλ控制的性能。以下分别是在空载、负载、去载3种工况下的对比波形与分析。

电机空载起动，仿真时间为4 s，分别对分数阶PIλ和普通PI的转速n和转矩T的波形图进行对比与仿真。

由图5和图6波形对比可以得出，普通PI控制的转速在0～0.5 s内到达稳定时间为0.151 s，超调量为0.2%；而分数阶PIλ在0～0.5 s内到达稳定时间为0.139 s，超调量为0.3%。分数阶PIλ比普通PI控制虽然超调量更大，但是转速更早达到稳定值。

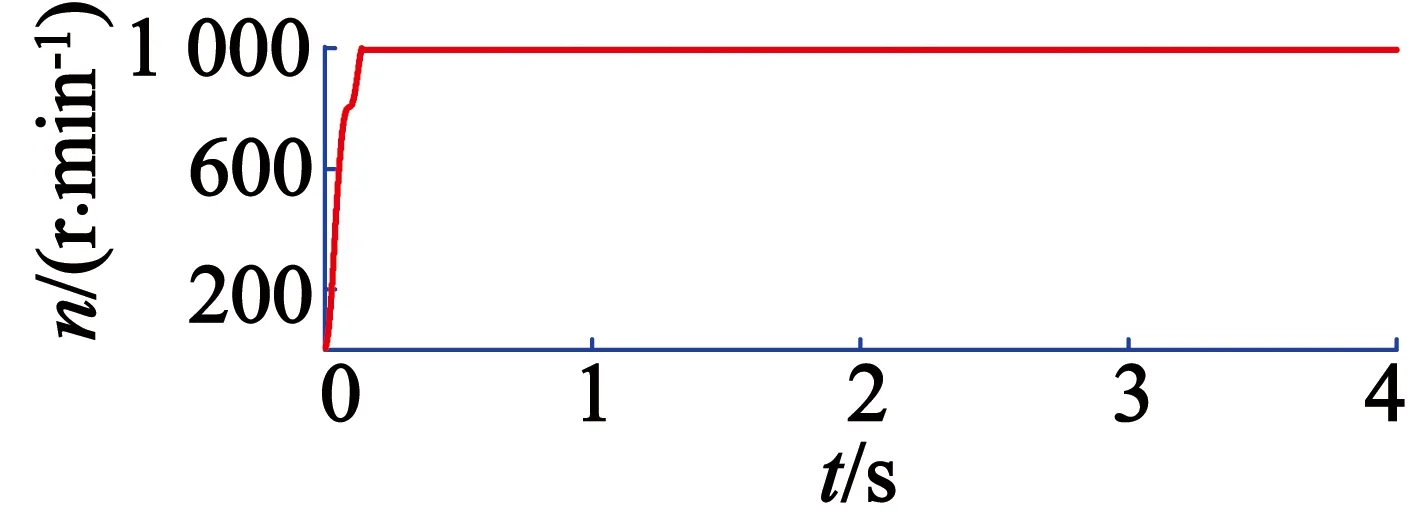
图5 普通PI控制空载下的转速响应曲

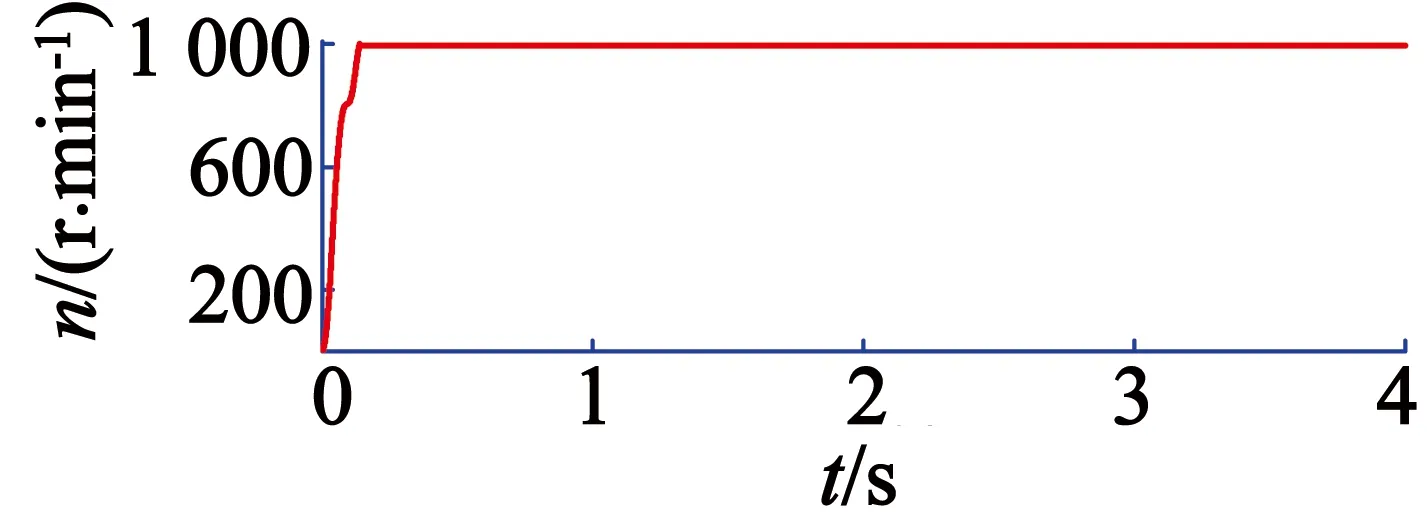
图6 分数阶PIλ控制空载下的转速响应曲线

由图7和图8波形对比可以得出，虽然稳定时普通PI控制下的波动更小，但是分数阶PIλ控制下转矩达到稳定时间为0.150 s，比普通PI稳定时间0.161 s更短。

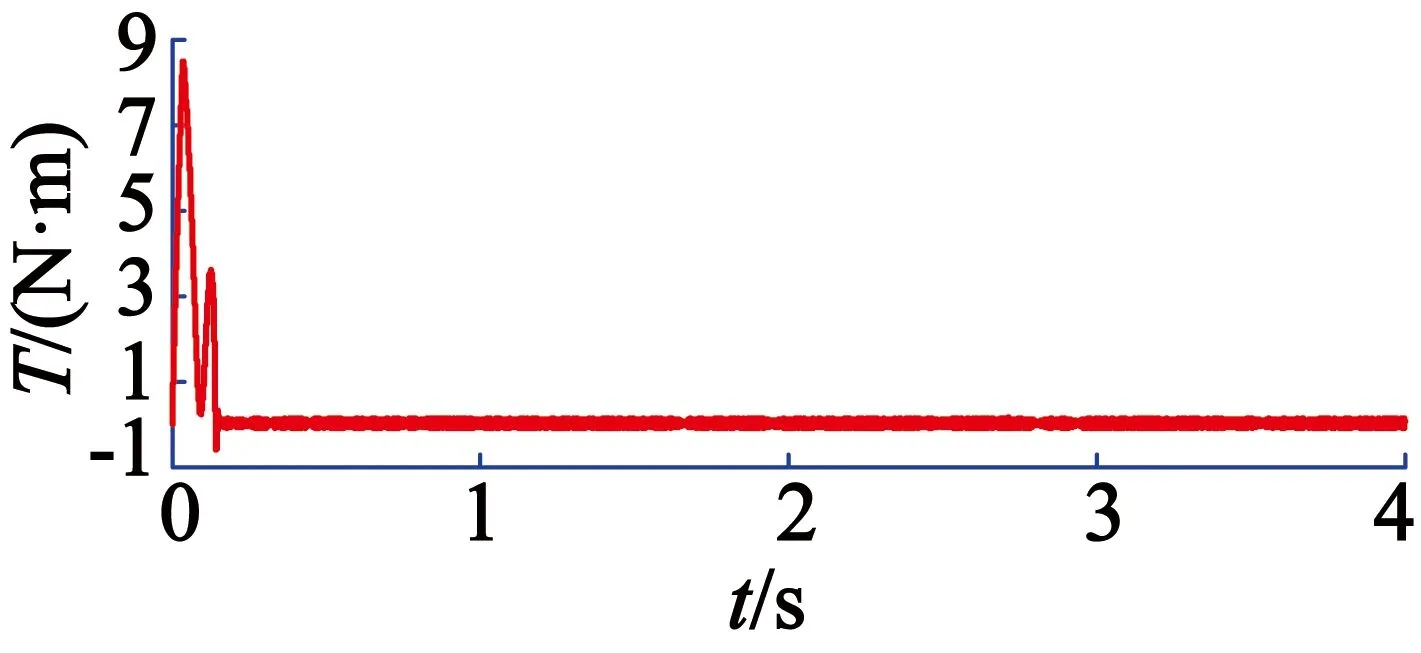
图7 普通PI控制空载下的转矩响应曲线

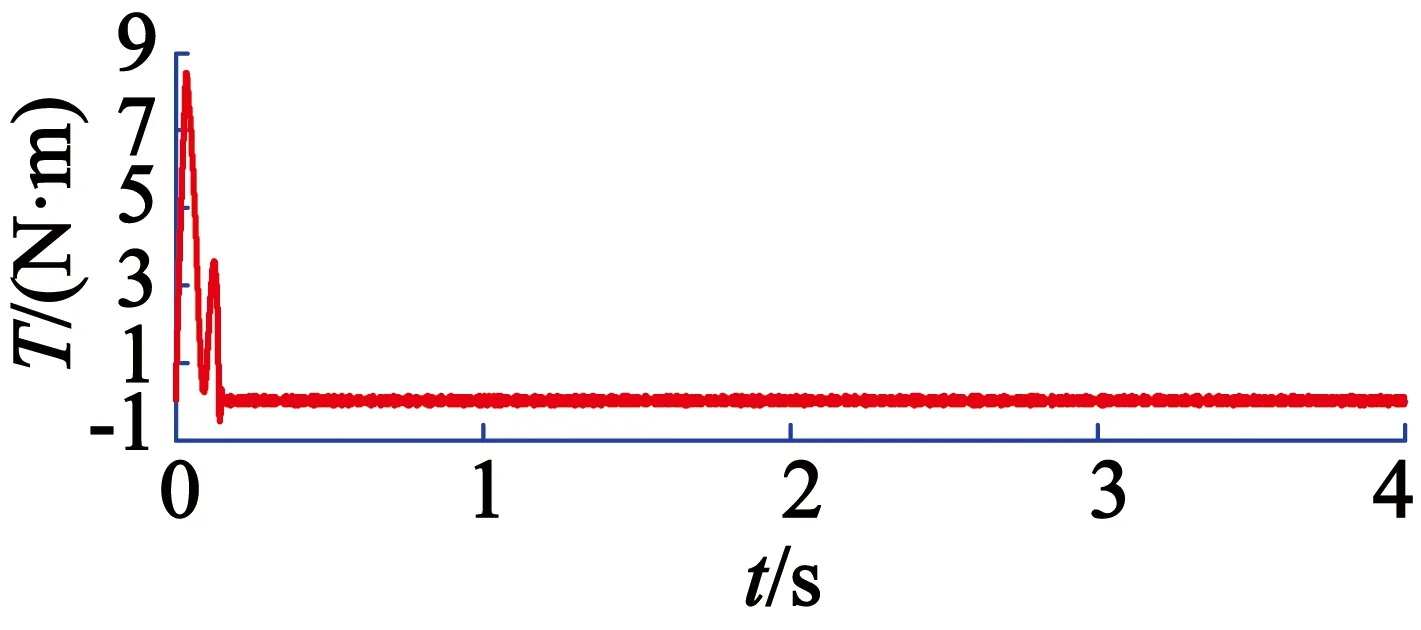
图8 分数阶PIλ控制空载下的转矩响应曲线

电机在0～2 s间无负载启动，2 s时加入负载转矩1.3 N·m仿真时间为4 s，以下分别分数阶PIλ和普通PI转速n和转矩T的波形图进行仿真与对比。

由图9和图10波形对比可以得出，与普通PI在0.151s达到额定转速相比，分数阶PIλ在0.138 s更早达到稳定值且无超调。2 s时加入负载转矩1.3 N·m，转速开始下降，普通PI控制在2.012 s达到稳定值，而分数阶PIλ在2.002 s更早达到稳定且脉动更小。

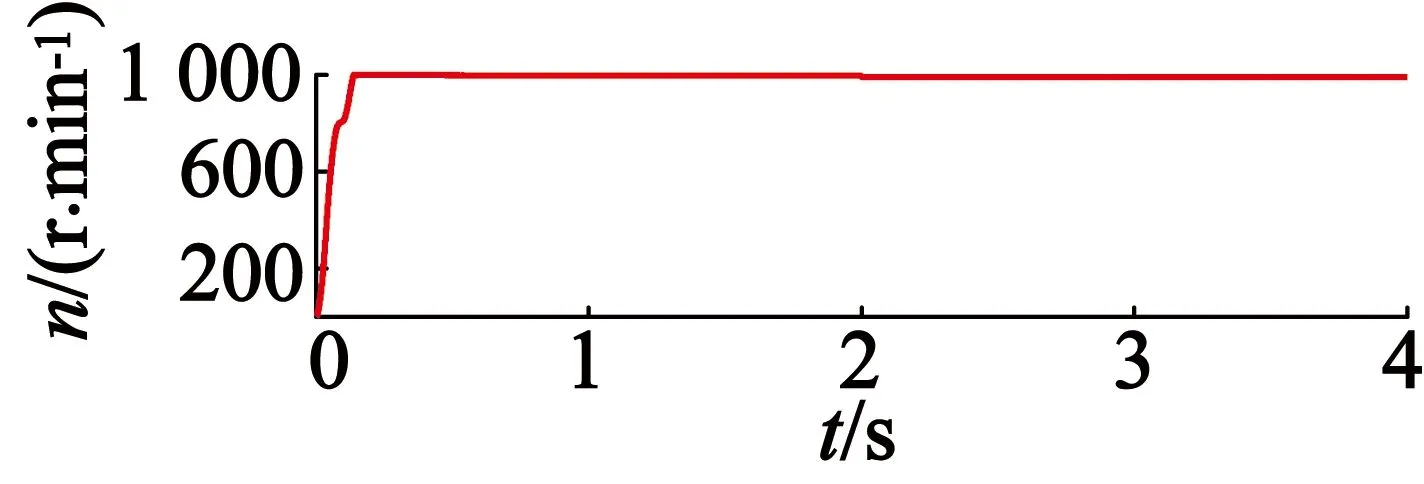
图9 普通PI控制负载下的转速响应曲线

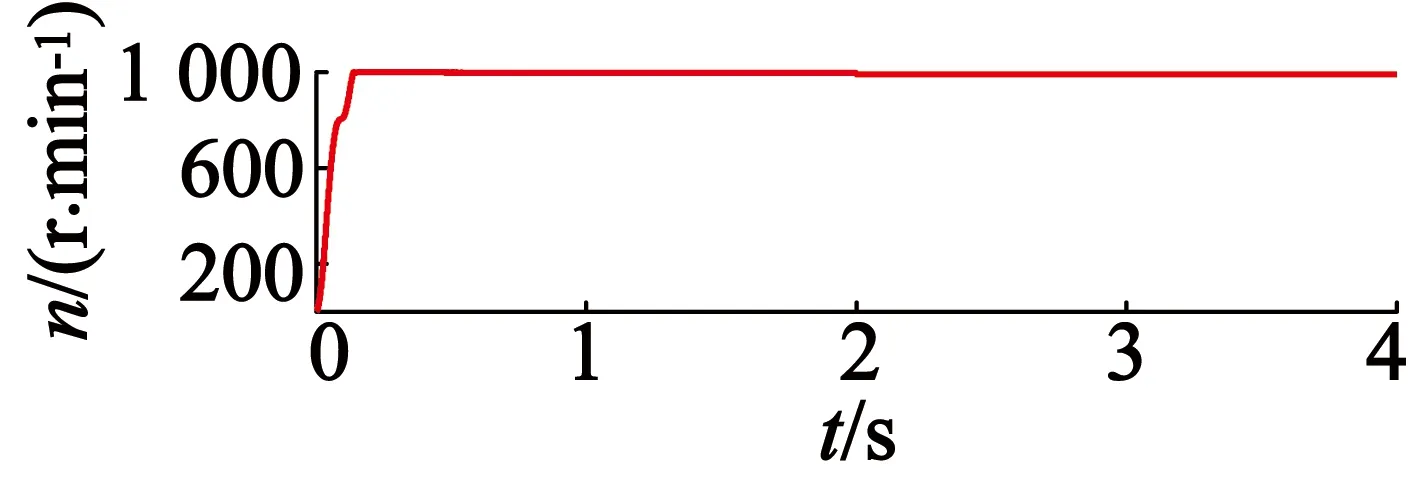
图10 分数阶PIλ控制负载下的转速响应曲线

通过以上转速和转矩波形的比较得出，转矩和转速成反比的关系，证明本文的设计是正确的。在分数PIλ的控制下，电机在0.150 s达到稳态，匀速运转。与普通PI控制在0.152 s达到稳态相比，分数阶PIλ更早达到稳态且超调更小。由于在2 s加入1.3 N·m负载转矩，电机的转矩发生变化，分数阶PIλ在2.010 s达到另一个稳态值1.3 N·m，并且有少许的波动。从图11、图12的对比来看，分数阶PIλ控制的调速性能总是优于普通PI控制。

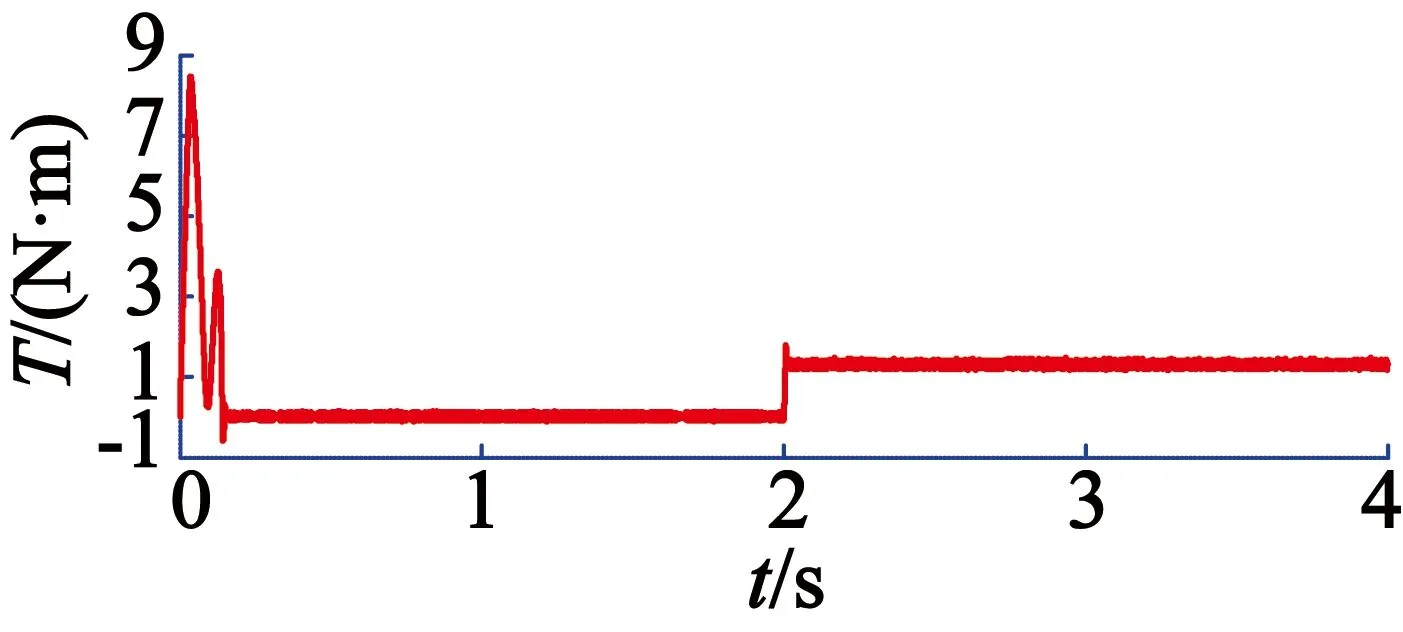
图11 普通PI控制负载下的转矩响应曲线

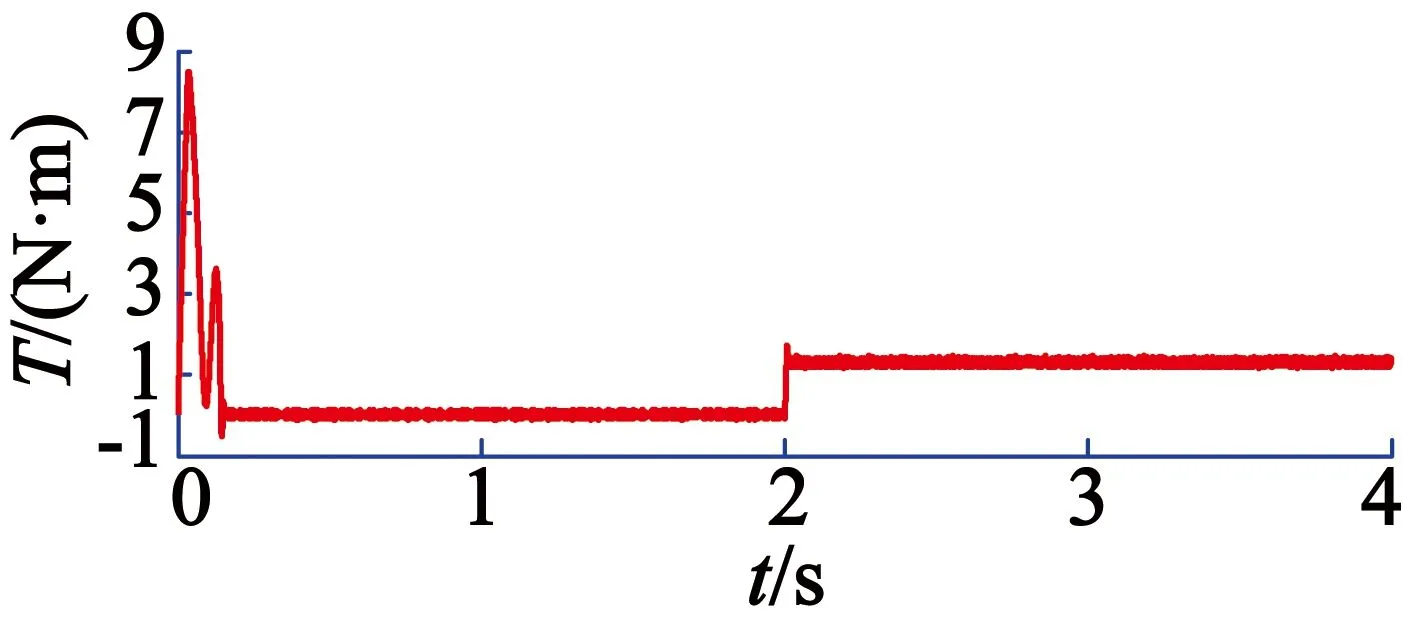
图12 分数阶PIλ控制负载下的转矩响应曲线

电机在0～2 s间负载转矩1.3 N·m，2 s时负载转矩为零，仿真时间为4 s。以下分别为转速n和转矩T的波形图进行仿真与对比。

由图13和图14波形对比可以得出，电机带初始负载转矩启动，普通PI在0.28 s时第一次达到稳定值，转速为988 r/min。在2 s去载，转速增加，在2.010 s时达到另一个稳定值992 r/min。分数阶PIλ控制在0.27 s时第一次达到稳态值，转速为996 r/min。在2 s去载，转速增加，在2.008 s时达到另一个稳态值997 r/min。因此分数阶PIλ更早达到稳态，更接近额定转速，并且波动更小。

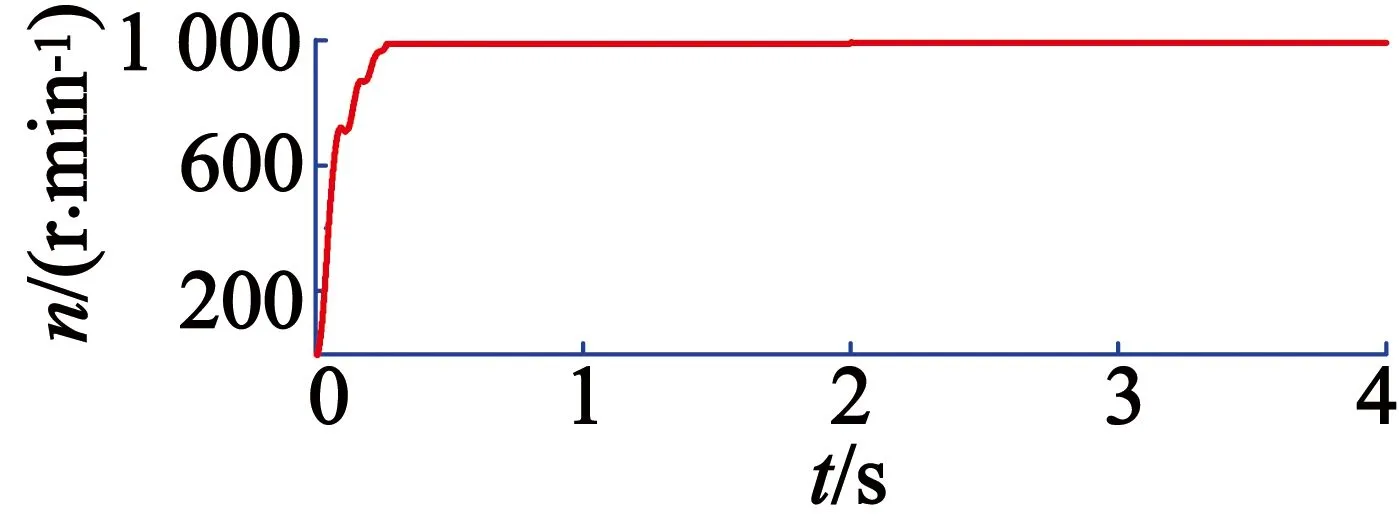
图13 普通PI控制去载下的转速响应曲线

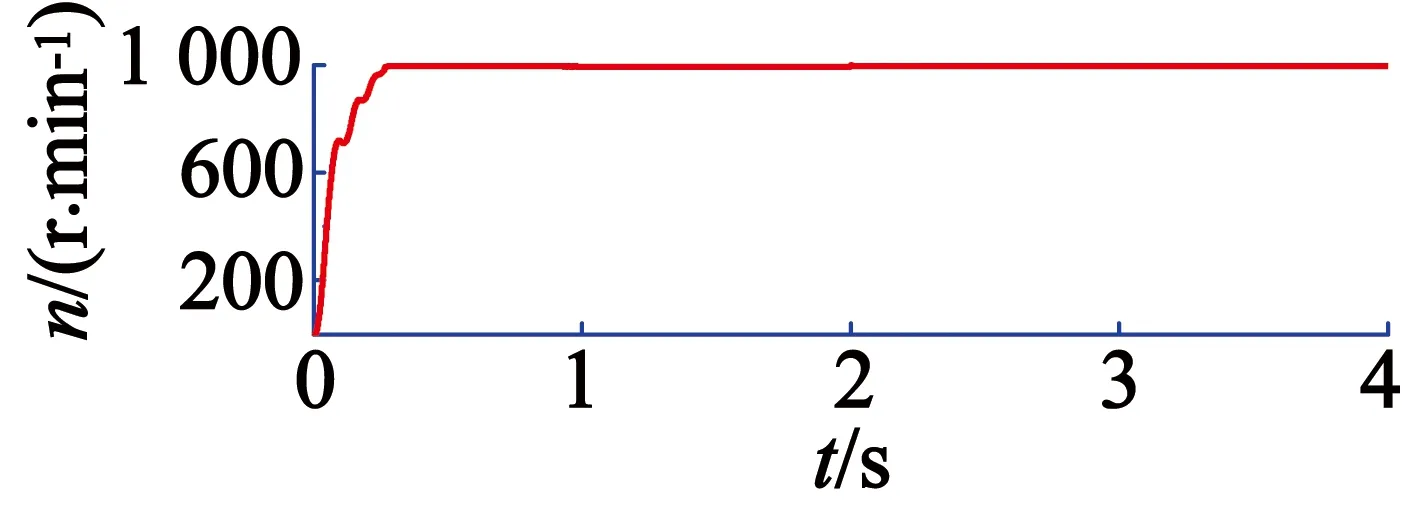
图14 分数阶PIλ控制去载下的转速响应曲线

由图15和图16波形对比可以得出，普通PI控制下，在0.29 s第一次达到稳态值1.3 N·m在2 s时去载时，在2.010 s负载转矩稳定。从图中可以看出，分数阶PIλ控制在0.27 s第一次转矩达到稳态值1.3 N·m，在2 s时去载后，2.006 s达到稳态，可见分阶数PIλ转矩能更早达到稳态。

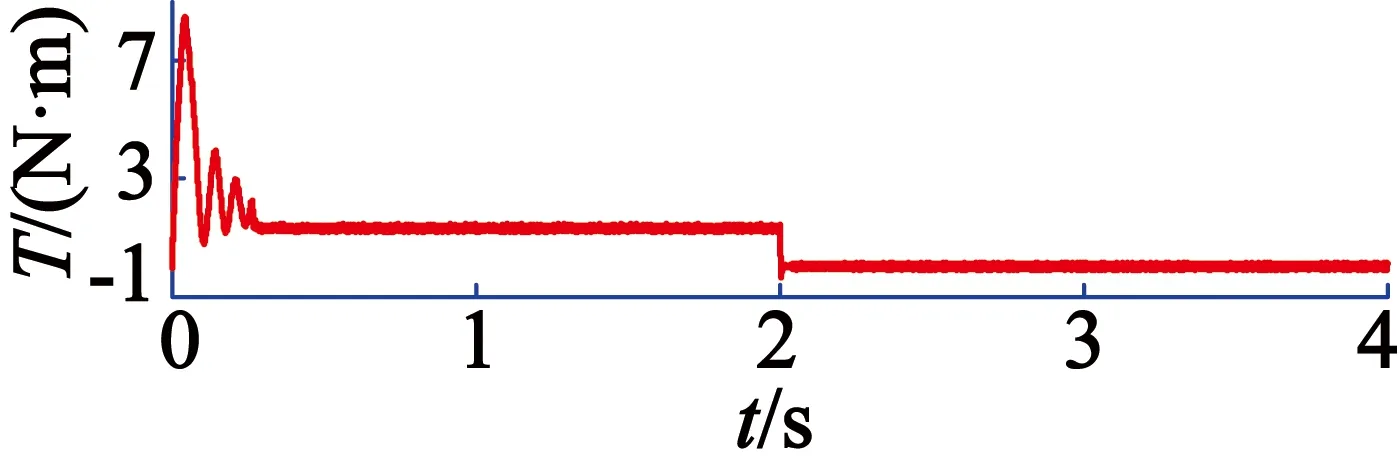
图15 普通PI控制去载下的转矩响应曲线

图16 分数阶PIλ控制去载下的转矩响应曲线

2.2.2不同阶数λ之间的仿真与对比

通过对不同阶数λ之间的仿真与对比，以寻求最佳值。对于分数阶PIλ控制器最优值选取，我们在0.1～0.9之间分别取值仿真。比阶数在0.7和0.8下控制的电机更稳定，故在此细化对比阶数取值0.7和0.8的情况。下面通过对λ为0.7与0.8的情况分空载、负载、去载进行数据对比，说明如何分析得出最佳分数阶PIλ控制器阶数值。

电机空载启动，仿真时间为4 s，表2为空载时，六相无刷直流电机分数阶PIλ控制节数λ为0.7与0.8的转速n和转矩Te、反电动势Eabc、电流Iabc的波形对比表格。

表2 空载实验下阶数取值0.7与0.8数据对比

电机在0～2 s，负载转矩1.3 N·m，2 s时负载转矩为零，仿真时间为4 s。表3为负载时，六相无刷直流电机分数阶PIλ控制阶数λ为0.7与0.8的转速n和转矩Te、反电动势Eabc、电流Iabc的波形对比表格。

表3 负载实验下阶数取值0.7与0.8数据对比

电机在0～2 s间，负载转矩1.3 N·m；2 s时负载转矩为零，仿真时间为4 s。表4为去载时六相无刷直流电机分数阶PIλ控制λ为0.7与0.8的转速n和转矩Te、反电动势Eabc、电流Iabc的波形对比表格。

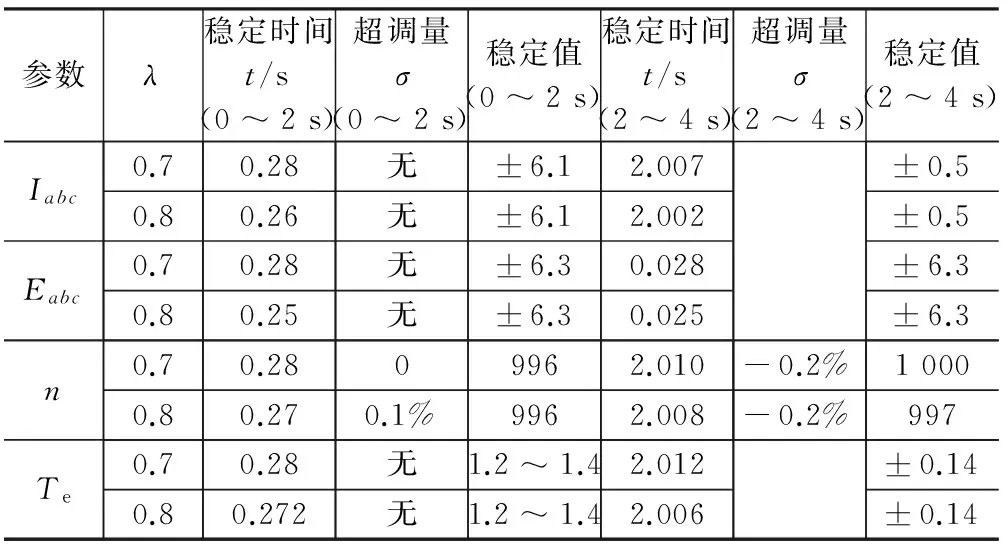
表4 去载实验下阶数取值0.7与0.8数据对比

当阶数取值为0.8时往往能比阶数取值0.7时更快达到稳定值，并且波形脉动小,所以我们取λ数值为0.8。

3 结 语

本文以六相无刷直流电机控制系统为研究对象，将分数阶PIλ控制器进行最优化设计并与普通PI控制器进行仿真比较。通过MATLAB电机模型上的仿真实验结果表明：普通PI控制器和分数阶PIλ控制器(阶数λ在0.5～0.9之间)相比，无刷直流电机通过分数阶PIλ的控制方式，能使电机达到额定转速并且转矩的波动更小。且当分数阶PIλ控制器的阶数为0.8时，控制效果最佳。同时通过分数阶PIλ的控制方式克服了电机非线性的缺点，具有较强的适应能力，分数阶PIλ控制具有更广阔的发展前景。

[1] 夏长亮,方红伟.永磁无刷直流电机及其控制[J].电工技术学报,2012,27(3):25-34.

[2] 朱光起.基于十二拍控制模式的无刷直流电机速度控制策略研究[D].哈尔滨：哈尔滨工业大学,2013.

[3] 张晓红，赵显红.直流无刷电机控制系统的研究[J].微计算机信息，2009,(2)：146-147.

[4] 计晶.基于DSP的无刷直流电机调速系统的设计与实现[D].北京：北京印刷学院，2014.

[5] 侯磊.无位置传感器无刷直流电机调速系统的研究[D].济南：山东大学，2007.

[6] 徐伟，屈百达，徐保国，等.基于模糊PID模型的无刷直流电机转速控制[J].科学技术与工程,2010,10(32)：7926-7929.

[7] 成都贝翔科技有限公司.多控制模式无刷直流电机控制系统：202231657U[P],2012-05-23.

[8] 吴凌燕，蔡岗.BLDCM在Simulink中的图形化仿真与分析[J].太原师范学院学报(自然科学版)，2010，9(4):63-65.

[9] 田小敏.智能分数阶PID控制器的研究[D].合肥：安徽理工大学，2012.

[10] PODLUBNY I.Fractional-order systems and PID controllers[J].IEEE Transactions on Automatic control. 2009,44(1):208-214.

[11] CHATTOPADHYAY S,BANDYOPADHYAY M.Simplified method of speed control of a DC Motor through DAS using MATLAB-based PID controller and study of its application in a voltage control system of a DC generator[J].International Journal of Measurement Technologies and Instrumentation Engineering (IJMTIE),2013,3(4):68-76.

[12] KUMAR N S,KUMAR C S.Design and implementation of adaptive fuzzy controller for speed control of brushless DC motors[J].International Journal of Computer Applications,2010,1(27):36-41.

Analysis and Simulation on Fractional Order PIλControl of Six Phase Brushless DC Motor

PENGSheng-nan,LIUXiao-bing,LONGJu

(Xihua University,Chengdu 610039,China)

established the approximate formula of fractional order PIλ, and the simulation model of the fractional order PIλspeed control system and common PI control are built in the MATLAB/Simulink environment. The simulation experiment results show that compared to the ordinary PI control, when the fractional order PIλcontrol in the order value is the range of 0.5～0.9, it not only can more quickly and accurately track the given speed, but also can load disturbances and parameter changes with better anti-disturbance ability and stability. Analyze the waveforms of different orders , and the optimal order of the PIλcontroller was 0.8 in the range of 0.5～0.9.

fractional order PIλ; brushless DC motor of six phase; MATLAB

2016-07-10

西华大学研究生创业基金项目(ycjj2016097)

TM33

A

1004-7018(2017)02-0051-04

彭晟楠(1993-),女，硕士研究生，研究方向为智能控制。