基于参数辨识的永磁同步电动机无位置传感器控制

陈达波

(重庆水利电力职业技术学院，永川 402160)

基于参数辨识的永磁同步电动机无位置传感器控制

陈达波

(重庆水利电力职业技术学院，永川 402160)

研究了基于参数辨识的永磁同步电动机无位置传感器控制算法。通过逆变器向电机绕组注入电压激励，根据其响应的电流来离线辨识电机的定子电阻和交轴电感。为了避免逆变器死区引起的辨识误差，采用差分的方式进行信号注入。利用辨识得到的电阻和电感值进行动态磁链的估计，结合软件锁相环估计出转子位置，从而能够在电机参数未知的情况下实现永磁同步电机的无传感器运行。通过实验验证了参数辨识算法和无传感器算法的有效性。

永磁同步电机；无位置传感器；动态磁链；参数估计

0 引 言

永磁同步电机(以下简称PMSM)通过在电机的转子上安装永磁体取代了励磁绕组，可以减小电机体积并且提高性能与可靠性，应用领域越发广泛[1]。

许多应用场合中，由于成本或体积限制，PMSM无法安装位置传感器，此时需采用无位置传感器的控制策略，利用逆变器采样到的电压电流估计出PMSM的转子位置。无传感器转子位置估计算法可以分为2类：第一类是基于信号注入的方法[2-3]，该类算法不需要电机参数，但是会引入高频噪声和转矩脉动，常用于低速段。第二类是基于定子绕组反电势的算法[4-5]，该类算法利用电机模型得到反电势信息，进而估计转子位置，但是需要准确的电机模型参数。实际应用中，第二类算法更为常用。

为了保证无传感器转子位置估计算法的准确性，需要对电机的参数进行精确的测量或辨识。为了避免测量的繁琐，将电机的参数辨识集成进驱动器成为了近年来的研究热点。文献[6]采用遗传算法来估计PMSM的参数，收获了良好的辨识结果。文献[7]采用模型参考自适应法估计电机参数，但要同时估计所有参数会导致算法的收敛速度很慢，甚至无法收敛。

本文介绍一种基于参数辨识的永磁同步电动机无位置传感器控制方法。首先向电机注入直流和交流电压激励，利用电流响应来辨识出定子电阻和交轴电感。同时采用差分注入的方式避免逆变器死区的影响。然后，采用动态磁链法估计转子位置并用于矢量控制，估计算法中用到的电阻和电感参数使用先前的参数辨识结果。最后，通过实验验证了该方法的有效性。

1 基于信号注入的参数辨识方法

本文使用的无传感器控制方法需要用到电机2个电气参数，分别是定子电阻Rs和交轴电感Lq。下面论述使用逆变器对PMSM参数进行辨识的方法。

1.1 定子电阻辨识

首先将电机转子强制定位在特定位置θr=0处，然后在d轴注入直流电压，q轴电压为零，即Ud=Udm,Uq=0。由于不存在转矩分量，这样仍可使电机转子保持在静止状态。由PMSM的d-q轴坐标系方程:

在转子静止且电流恒定的稳态下，方程简化为：

通过检测d轴电流响应即可计算得到定子电阻Rs=ud/id。在实际辨识过程中，为了防止上下桥臂同时导通造成短路，在导通和关断之间加入了一段死区延时。死区会造成实际输出电压和期望输出电压之间有偏差。该偏差跟电流的方向和大小有关，但是在负载变化不大的情况下，可以认为该误差的平均值是不变的。

考虑死区影响时，式(2)变为：

(3)

其中，Dd是d轴给定占空比，ΔD是死区所占的占空比，Ubus是母线电压，由AD采样得到。

进而有：

(4)

其中ΔRs为死区效应导致的辨识误差。

若采用差分注入的方式，注入2个幅值不等的Ud，即:

(5)

(6)

式(5)乘以Ubus2，式(6)乘以Ubus1，两式相减，有：

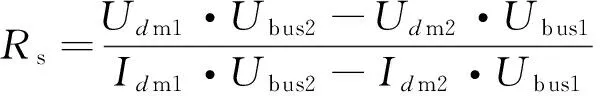
(7)

从而可以在死区时间ΔD未知的情况下通过检测电流差值进行计算，准确得到Rs。

特别地，若母线电压Ubus恒定，式(7)简化为：

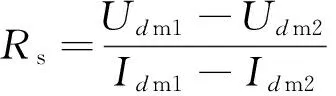
(8)

1.2 交轴电感辨识

仍将电机转子强制定位在θr=0处，电机在静止(ωr=0)状态下dq轴系方程简化为：

在q轴注入角频率为ω的正弦激励电压，即：

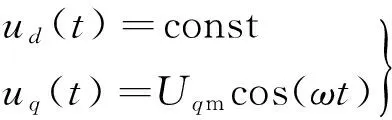
(10)

注意到，为了保证电机转子不转动，在q轴注入正弦激励电压信号的同时，需要在d轴注入一个直流定位电压恒量，而且q轴注入的正弦电压频率要适当高一些，其理论分析如下。

当采用式(10)的注入方式时，电机定子磁场是在d轴附近往复振动的磁场，定子磁场对永磁体施加的电磁转矩可以描述成:

(11)

考虑电机的机械方程：

(12)

从而转子转速可以由图1得到。

图1 高频振动磁场下的电机转速

由于1/(Js+B)环节具有低通滤波的效果，因此当q轴注入频率足够高的时候，高频振动磁场不会产生转速，电机仍然保持静止。

稳态情况下用相量分析，q轴的电压激励：

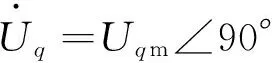
(13)

由式(9)可得激励信号频率为ω时q轴阻抗：

(14)

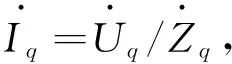
(15)

在此基础上，由Uqm,Iqm求取阻抗。与辨识定子电阻一样，为了避免逆变器PWM死区引起的电压幅值误差，同样使用差分方式，在同一频率下注入2个幅值不同的正弦电压，并检测当前频率下响应电流的幅值，计算出该频率下的阻抗值：

(16)

进而可以得到q轴电感表达式：

(17)

当定子电阻Rs和交轴电感Lq辨识出来之后，便可用于无传感器转子位置估计算法。

2 基于动态磁链的位置估计算法

动态磁链概念通过引入转子附加磁链，将凸极PMSM的转矩控制等效为隐极机的转矩控制。定义动态磁链:

(18)

则转矩表达式可以写成：

(19)

式(19)表明通过引入动态磁链凸极机的转矩表达式与隐极机转矩表达式相同，而动态磁链中引入的附加磁链为d轴电流与d，q轴电感差值的乘积，其方向与id同方向。又由于id与转子磁链同方向，因此动态磁链与转子磁链同方向，则通过观测动态磁链的方向即可获得转子位置。

根据式(1)建立PMSM的空间矢量方程：

通过引入积分运算，可以得到建立在静止两相α-β坐标系下的动态磁链矢量观测器：

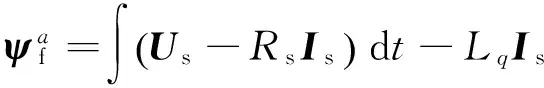
(21)

其中各个矢量定义如下：

此时采用如图2所示的软件锁相环就可以得到转子的速度和位置。

图2 基于反电势积分法的转子位置估计算法

从式(21)可以看出，基于动态磁链的位置估计算法需要用到积分器，而在实际系统中，电流采样的直流偏置会造成积分器的溢出，因此需改进积分器结构避免直流偏置带来的溢出。常用的方法是使用低通滤波器形式的改进积分器，即引入一个非常低的截止频率，使低通滤波器对直流的增益为有限值。

从推导中看到，基于动态磁链概念的位置估计算法可将凸极机的控制等效为隐极机，其算法只需使用到2个电气参数，即定子电阻Rs和交轴电感Lq。由于不需要用到直轴电感Ld和永磁体磁链ψf，就降低了参数辨识的复杂度，从而，使用式(8)和式(17)的电阻电感计算公式就可以满足无传感器算法对参数辨识的需求。

3 实验验证

为了验证上述基于参数辨识的永磁同步电动机无位置传感器控制方法的有效性和实用性，在一台凸极性PMSM上进行了实验。其标称参数如下：定子电阻0.71 Ω，d轴电感6.2 mH，q轴电感7.8 mH。

本文的实验平台采用ST公司的低成本32位定点处理器STM32F103作为控制芯片，系统时钟设为72 MHz。功率模块采用TI的IPM，型号为DRV8432，其开关频率设为20 kHz。为了验证无传感器位置估计算法的性能，安装了1 024线的光电编码器作为对比。PMSM采用矢量控制方式，控制框图和实验平台如图3、图4所示。首先在电机静止状态下注入直流和交流激励，通过电流响应获取电机参数Rs,Lq，然后利用动态磁链的方法获得转子位置并用于电机的矢量运行。电机运行时，采用MTPA的控制方法来提高电流利用率。

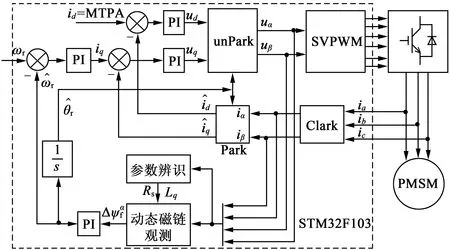
图3 PMSM矢量控制框图

图4 实验平台图

3.1 参数辨识实验

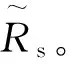
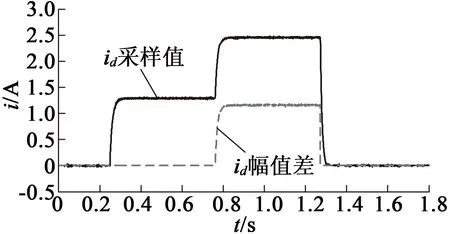
图5 实验平台图

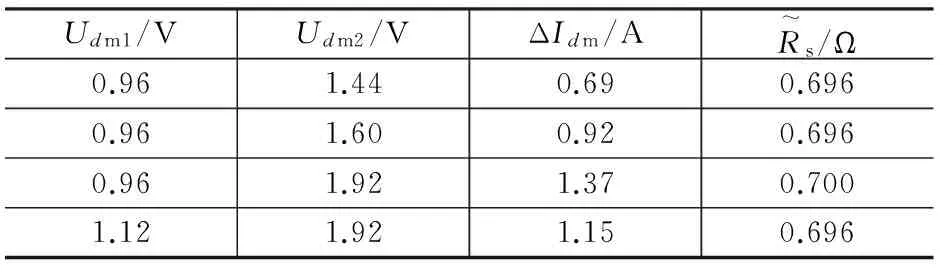
Udm1/VUdm2/VΔIdm/AR～s/Ω0.961.440.690.6960.961.600.920.6960.961.921.370.7001.121.921.150.696

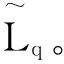
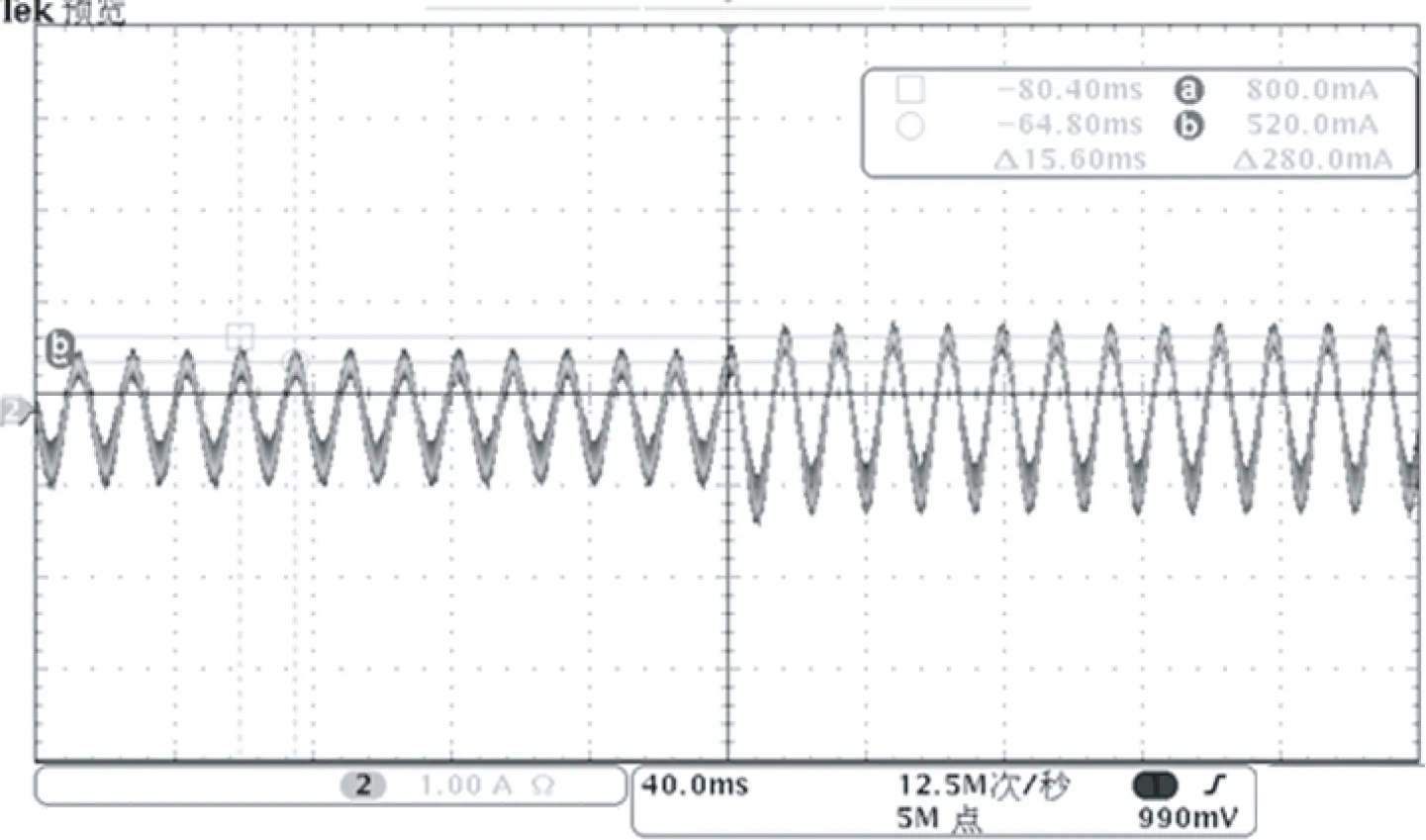
图6 交轴电感辨识时的交轴电流(截图)

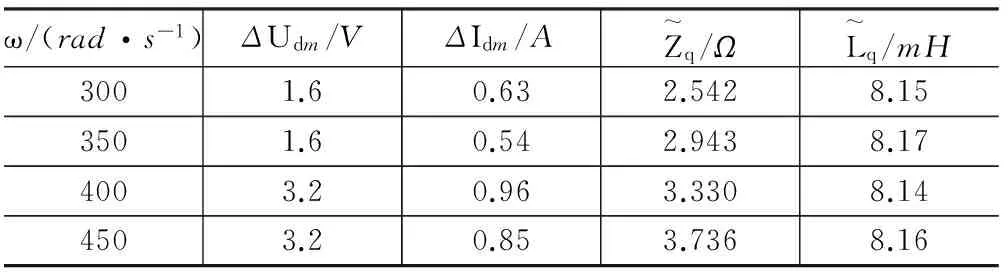
表2 交轴电感的辨识结果

因此，采用本文介绍的基于信号注入的参数辨识方法可以准确获得PMSM的定子电阻和交轴电感值，其辨识精度可以满足无传感器算法的要求。

3.2 位置估计实验

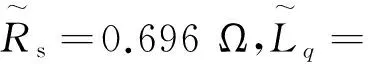
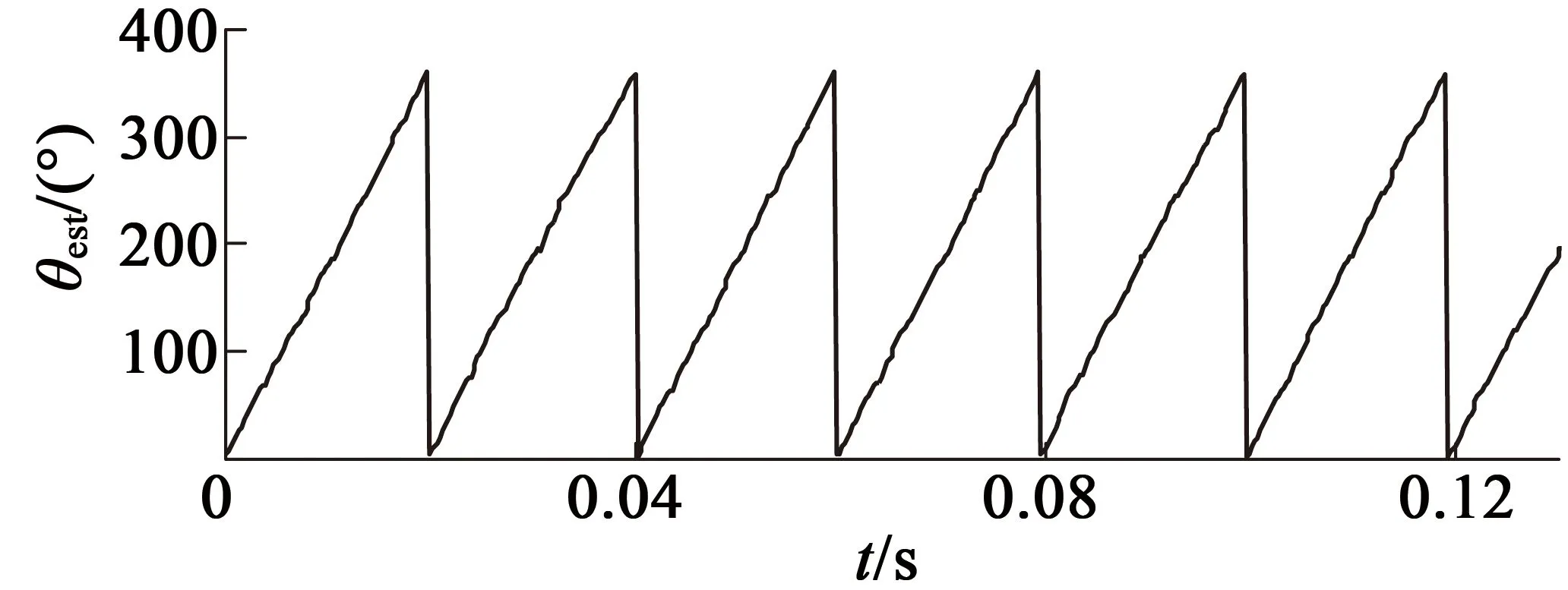
(a) 估计转子位置

(b) 位置估计误差

图8为采用的控制算法时PMSM的调速性能。电机从1 000 r/min升速到3 250 r/min，再逐渐降速。可以看到，当采用基于参数辨识的永磁同步电动机无位置传感器控制时，PMSM的实际转速能够准确跟踪给定指令，转速估计误差控制在±10 r/min内。这表明该算法能够保证PMSM的调速性能。

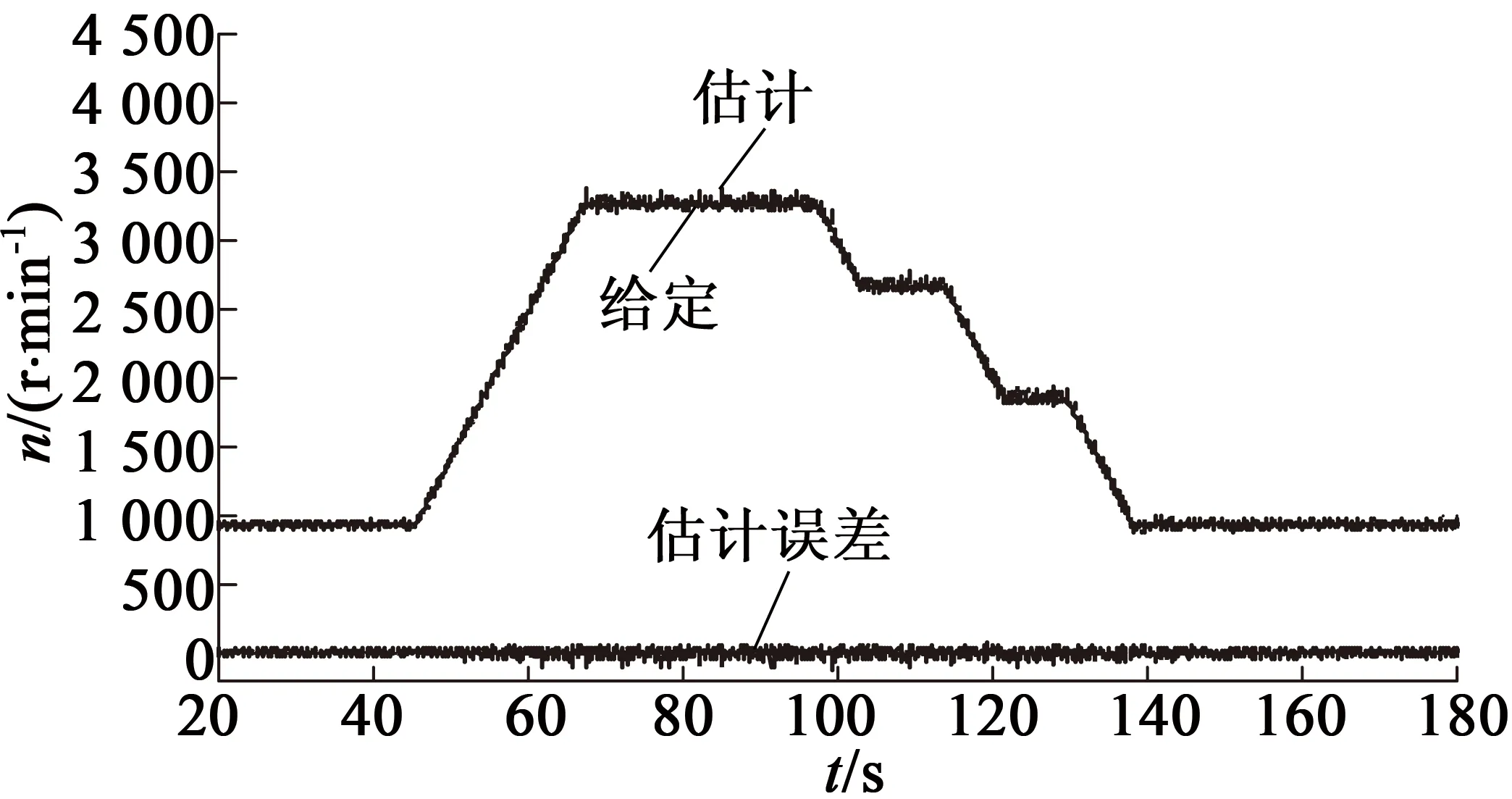
图8 采用所提算法的PMSM调速性能

4 结 语

本文针对PMSM的无传感器控制及其参数辨识需求，介绍了一种基于参数辨识的PMSM无传感器控制算法。通过逆变器注入合适类型的电压信号，从电流响应中获取电机的参数信息，为了避免死区的影响，采用差分形式注入，辨识得到的电阻和电感值可以用于PMSM的转子位置估计。本文采用基于动态磁链的位置估计算法，实现简单，且只要求定子电阻和交轴电感的参数。通过实验验证了该方法的有效性，参数辨识和位置估计的性能都能够满足无传感器控制的要求，采用本文介绍的算法可以获得很好的调速性能。

[1] 王成元,夏加宽,杨俊友,等.电机现代控制技术[M].北京：机械工业出版社,2006.

[2] JANG J H,SUL S K,HA J I,et al.Sensorless drive of surface-mounted permanent-magnet motor by high-frequency signal injection based on magnetic saliency[J].IEEE Transactions on Industry Applications,2003,39(4):1031-1039.

[3] 王高林,杨荣峰,于泳,等.内置式永磁同步电机无位置传感器控制[J].电机与控制应用,2010(30):93-98.

[4] PAICU M C,BOLDEA I,ANDREESCU G D,et al.Very low speed performance of active flux based sensorless control:interior permanent magnet synchronous motor vector control versus direct torque and flux control[J].IET Electric Power Applications,2009,3(6):551-561.

[5] LEE H,LEE J.Design of iterative sliding mode observer for sensorless PMSM control[J].IEEE Transactions on Control Systems Technology,2013,21(4):1394-1399.

[6] 肖曦,许青松,王雅婷,等.基于遗传算法的内埋式永磁同步电机参数辨识方法[J].电工技术学报,2014,29(3):21-26.

[7] 陈振锋,钟彦儒,李洁.嵌入式永磁同步电机自适应在线参数辨识[J].电机与控制学报,2010,14(4):9-13.

Sensorless Control of Permanent Magnetic Synchronous Motor Based on Parameter Identification

CHENDa-bo

(Chongqing Water Resources and Electric Engineering College,Yongchuan 402160,China)

A method of sensorless control of permanent magnetic synchronous motor based on parameter identification is proposed. Voltage signal was injected to the motor via inverter, and the current response was used to off-line identify the stator resistance and cross-axis inductance. To avoid the adverse effect of inverter dead-zone on parameter identification, the injection signal was in the difference form. The identified resistance and inductance were used to estimate active flux, the rotor position was able to be obtained combing software phase locked loop. The sensorless control of motor could be achieved even though the electric parameters were unknown. The validity of the proposed method is verified by ample experiments.

permanent magnet synchronous motor; position sensorless; active flux; parameter estimation

2016-07-17

TM341;TM351

A

1004-7018(2017)02-0079-04

陈达波(1983-)，男，硕士，讲师，注册电气工程师，研究方向为电力系统自动化。