基于十八区段的PMSM高性能转矩控制

邢 岩，王 旭，杨 丹，张志美

(1.通化师范学院，通化 134002；2.东北大学，沈阳 110819)

基于十八区段的PMSM高性能转矩控制

邢 岩1，王 旭2，杨 丹2，张志美2

(1.通化师范学院，通化 134002；2.东北大学，沈阳 110819)

传统直接转矩控制采用6扇区的圆形磁链控制，扇区边界处电压矢量对定子磁链的作用效果不对称的问题，导致磁链和转矩脉动大，而且在考虑定子电阻压降时，电压矢量选择表存在误差。针对上述问题，推导了定子电压矢量对磁链的控制公式，分别分析了忽略和考虑定子电阻压降影响时的定子磁链性能，提出了十八区段控制方法及改进的电压矢量选择表。比较传统直接转矩控制和十八区段直接转矩控制的系统性能，结果表明十八区段直接转矩控制在保持算法简单、动态响应迅速的基础上，能够有效地降低磁链和转矩脉动。

永磁同步电动机；直接转矩控制；磁链和转矩脉动；十八区段

0 引 言

直接转矩控制因具有鲁棒性强，动态响应快，不需要旋转坐标系变换模型简单，实现内部转矩闭环时不需要转子位置信息[1-3]等优点而受到越来越多的关注[4]。1986年DTC策略首次在感应电机控制系统中提出[5]，之后直接转矩控制策略受到广泛重视，国内外学者对DTC策略进行了深入研究，促进了DTC的理论发展和实际应用[6-10]。

直接转矩控制摒弃了解耦的思想，把磁链空间分成6个扇区，采用滞环比较器控制磁链和转矩，实现了对磁链和转矩的直接控制。滞环比较器的应用使得控制系统动态响应快，对参数依赖少，但它需要用到定子磁链的位置信息。当定子电阻随电机温度变化带来测量误差时，会导致定子磁链扇区选择不准确，影响电动机控制系统的性能。本文详细阐述了DTC系统中定子磁链性能，提出十八区段控制方法、相应的电压矢量选择表及其实现方法。理论分析和仿真实验表明十八区段方法磁链增量在区段分界处基本对称，可以有效减小磁链和转矩脉动。

1 传统DTC定子磁链性能分析

直接转矩控制中对定子磁链和电磁转矩的控制是在α-β两相静止坐标系下实现的，永磁同步电机在α-β两相静止坐标系下的电压方程可写成：

(1)

式中：us为定子空间电压矢量，在不同的时刻，us分别代表空间电压矢量U1，U2，U3，U4，U5，U6；is为定子电流；ψs为定子磁链;Rs为定子电阻。

忽略定子电阻压降时，得到定子电压与定子磁链的关系式：

(2)

假定控制系统采样周期为T，将式(2)离散化可得：

(3)

式(3)描述了一个采样周期内空间电压矢量us对定子磁链矢量的作用，图1为其对应的矢量图表示形式，图中θuψ为施加的空间电压矢量与定子磁链矢量之间的夹角；Δδ为负载角变化量。

图1 电压矢量对磁链矢量的影响

进一步给出空间矢量与磁链变化幅度间的定量关系式，即一个采样周期内，在us的作用下磁链幅值的变化量：

在θ1扇区，逆时针方向旋转时，施加电压矢量U2或U3分别控制幅值|ψs|增加或减小，记定子磁链矢量与U2的夹角为θuψ1∈(30° , 90°)，与U3的夹角为θuψ2∈(90° , 150°)，电压空间矢量幅值为|us|，根据式(4)一个周期内定子磁链变化量：

(5)

(6)

式中:θuψ1和θuψ2分别为定子磁链矢量ψs与U2,U3的夹角为θuψ2以扇区中心线为中心。根据上述关系，画出θ1扇区内，分别选择电压矢量时磁链幅值变化曲线，如图2所示。

(a)磁链幅值增加(b)磁链幅值减小

图2 传统DTC定子磁链变化曲线

图2中，θ表示则磁链ψs与θ1扇区中心线(即电压矢量U1)的夹角，θ∈(-30° , 30°)。

考虑定子电阻压降影响时，由式(1)得：

(7)

式中:Es为定子反电势矢量。设系统采样周期为T，将式(7)离散化可得：

(8)

进一步得到定子反电势矢量与磁链变化幅度之间的定量关系式：

(9)

式中:θeψ为定子反电动势矢量和定子磁链矢量之间的夹角。

而定子电压矢量和定子反电势矢量的夹角：

(10)

综上所述，可得到考虑夹角γ的影响时定子电压矢量对定子磁链幅值的作用效果，如图3所示。图3中角α为定子磁链矢量与扇区边界线之间的夹角。

图3 电压矢量对磁链幅值的影响

2 传统DTC电压矢量表存在的问题

传统DTC电压矢量中，当定子磁链ψs位于θ1扇区时，选择空间电压矢量U3为减小磁链增加转矩，选择空间电压矢量U5为减小磁链减小转矩[11-12]。实际上，当ψs位于图3中ψs1位置时，如果α角小于γ角，那么U3的作用是增加磁链增加转矩。同样，当ψs位于图3中ψs2位置时，如果α角小于γ角，那么空间电压矢量U5的作用效果是增加定子磁链幅值减小电磁转矩。其他扇区的分析及结论相同，即很难选出一个电压矢量，使得无论定子磁链处于一个扇区内的任何位置，都可以对定子磁链起到减小的作用。

综上所述，考虑定子电阻压降时，对于传统的6扇区分区方法，没有一个定子电压矢量，可以在一个扇区内始终控制定子磁链幅值减小。也就是说，传统直接转矩控制的电压矢量选择表在某些情况下是错误的，电机低速运行时定子电阻压降Rsis所占比例较大，这种错误尤为明显。

此外，由图2可以看出，一个扇区内定子电压矢量对定子磁链的作用是不对称的，在扇区边界线附近尤为明显。例如，当θ∈(-30°, -10°)时，一个周期内，磁链增加幅度很少，而磁链减小幅度很大，θ越小时这个差异越大。这将导致定子磁链在一个扇区内非均匀变化，磁链轨迹偏离理想圆，从而引起电流的畸变，影响系统性能。表1给出了定子磁链位于θi扇区时，施加电压矢量Ui+1和Ui+2引起的定子磁链幅值变化范围。

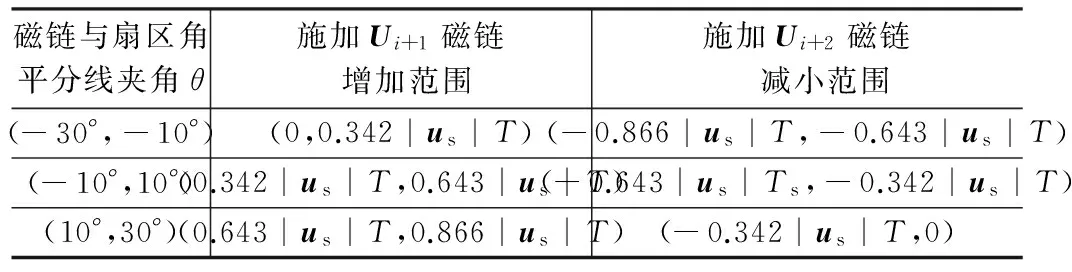
表1 扇区θi内磁链变化范围表

3 十八区段直接转矩控制及性能分析

3.1 十八区段直接转矩控制

由前面的分析可以看出，传统直接转矩控制的电压矢量选择表在某些情况下是错误的，电机低速运行时，这种错误更加明显。而且每个扇区内定子电压矢量对定子磁链的作用效果不对称，引起磁链脉动和电流畸变。

针对上述问题，本文提出了十八区段直接转矩控制方法。即将传统DTC的一个扇区细分成3个小区段，整个定子磁链空间分成18个区段(θ1,θ2, …,θ18)，每个区段为20°，如图4所示。根据定子电压对磁链和转矩的作用效果和图1可以推出十八区段的电压矢量选择表，如表2所示。

图4 定子磁链空间细分为18个区段示意图

表2 十八区段电压矢量选择表

根据表2，当定子磁链矢量处于图3中ψs1位置(α<γ)时，选择U4减小磁链增加转矩；当定子磁链矢量处于图3中ψs2位置(α>γ)时，选择U3减小磁链减小转矩，即表2中θ2区段和θ18区段对应的电压矢量。纠正了传统直接转矩中，当ψs位于图3中ψs1和ψs2位置并且α<γ时，选择U3减小磁链增加转矩，选择U5减小磁链减小转矩的错误。

3.2 磁链控制性能的分析

采用表2的电压矢量选择方法，考虑逆时针方向运行时，根据式(11)和式(12)作出一个区段内磁链幅值增加量和减小量的曲线，如图5所示。

(11)

(12)

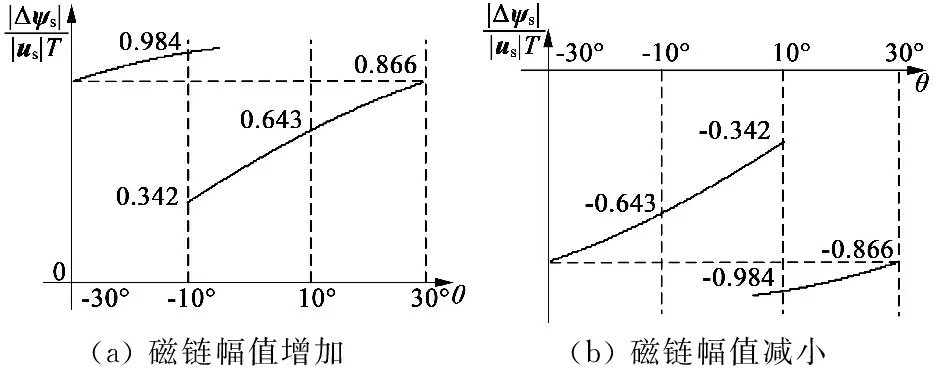
(a)磁链幅值增加(b)磁链幅值减小

图5 十八区段DTC磁链幅值变化曲线

十八区段方法中将原始的60°扇区划分为3个20°的区段，六扇区细分为18个区段。由图5可以看出，重新划分的每个小区段中磁链增加量和减小量基本对称。以定子磁链处于原始θ1扇区为例，此时θ∈(-30° , 30°)，分别列出θ∈(-30° , -10°)，θ∈(-10° , 10°)，θ∈(10° , 30°)这3个区段时，施加相应空间电压矢量时磁链增加和减小的范围，如表3所示。用同样的方法分析其余15个区段，其定子磁链幅值变化范围与上述3个区段相同。

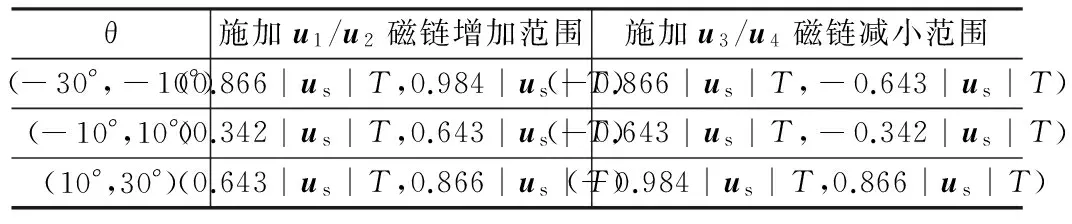
表3 扇区θ1内磁链变化范围

对照表1和表3可知，与传统DTC方法相比，十八区段划分方法，对空间电压矢量的选择更加细致、合理，有效解决了传统六扇区划分方法中扇区边界处磁链增加幅度和减小幅度不平衡的问题。

4 实验分析

为了验证所提出的新型直接转矩控制方法的有效性，本文对传统DTC和十八区段DTC进行了仿真实验，为了模拟实际电机运行，使用固定步长仿真算法中的ode4(Runge-Kutta)龙格-库塔算法，步长值设置为1×10-6s。电机参数：PN=1 kW,ωN=1 500 r/min,Rs=2.857 Ω,Ls=8.5 mH,p=2,ψf=0.175 Wb,J=0.000 8 kg·m2,B=0.000 1 N·m·s。仿真条件：系统参考转速为1 200 r/min，参考定子磁链为0.2 Wb，负载转矩为1 N·m，转矩比较器滞环宽度为0.1 N·m，磁链比较器滞环宽度为0.01 Wb。

图6和图7分别为相同条件下传统DTC方法和十八区段DTC方法的仿真波形，包括转速波形、定子磁链波形、转矩波形和定子电流波形。从图6(a)和图7(a)中可以看出，两种控制方法中电机转速均在0.2 s内达到参考值1 200 r/min，之后稳定运行于参考值，可见十八区段DTC保持了动态响应快这一优点。对比图6(b)和图7(b)，十八区段DTC对扇区的划分更加精细，因此磁链脉动大幅度降低，定子磁链运行轨迹更接近理想磁链圆，并且实际磁链圆的环宽变窄。由于定子磁链控制准确，定子磁链脉动降低，电磁转矩脉动也相应减小，如图7(c)所示。十八区段DTC系统的三相定子电流波形如图7(d)所示，可以看出三相定子电流对称，与图6(d)相比，图7(d)中定子电流谐波含量少，脉动小，波形曲线较细，控制系统性能有所提高。

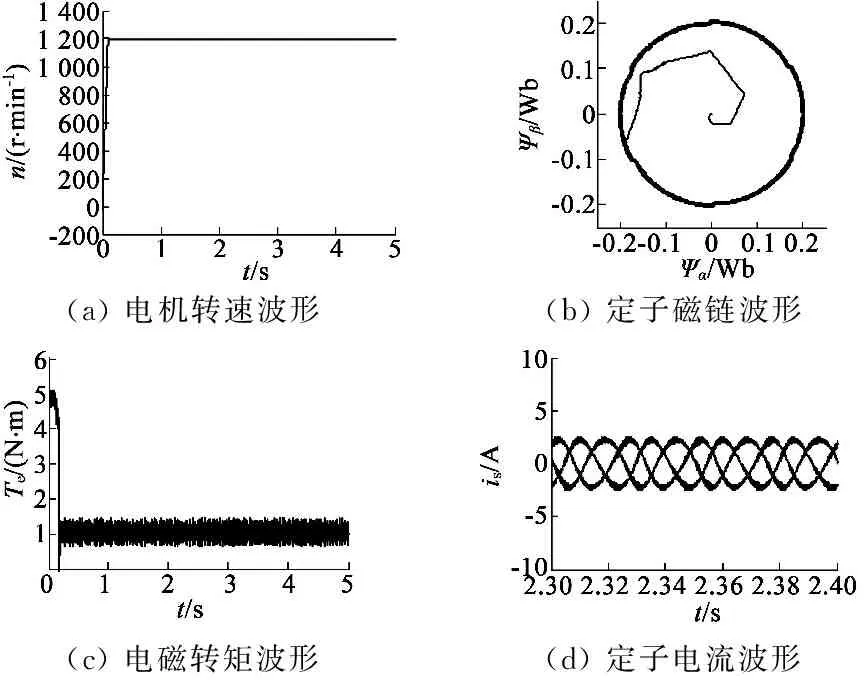
(a)电机转速波形(b)定子磁链波形(c)电磁转矩波形(d)定子电流波形

图6 传统直接转矩控制仿真波形

(a)电机转速波形(b)定子磁链波形(c)电磁转矩波形(d)定子电流波形

图7 基于十八区段的直接转矩控制仿真波形

从前面的对比可以看出，所提出的十八区段DTC方法具有与传统DTC相同的响应速度，但是磁链和转矩脉动明显降低，电流谐波含量明显减少。对2种控制方法中电机A相定子电流波形进行傅里叶分析。由于电机稳定运行时的转速为1 200 r/min，因此定子电流基波频率为40 Hz。分析时采用从2.05 s开始的10个周期波形，结果如图8所示。

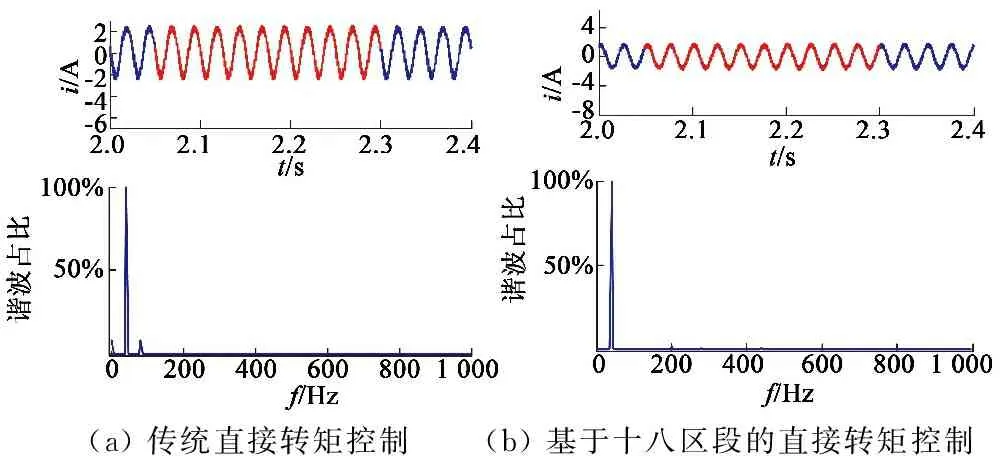
(a)传统直接转矩控制(b)基于十八区段的直接转矩控制

图8 不同控制策略时定子电流输出谐波

为了方便对比分析，表4给出两种DTC方法系统性能的比较结果。

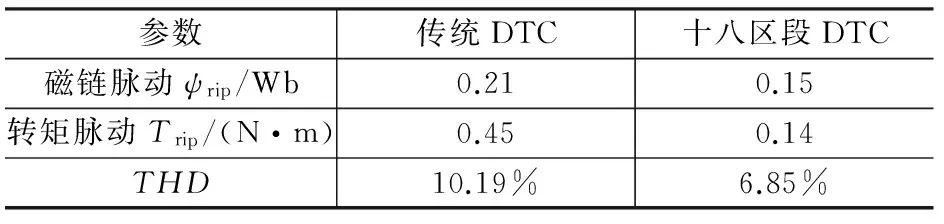
表4 两种控制方法系统性能比较

5 结 语

本文详细分析了传统直接转矩控制中定子磁链性能，指出电压矢量选择表存在的问题及磁链和磁链/转矩脉动产生原因,提出了十八区段直接转矩控制方法，推导了十八区段控制法电压矢量选择表和磁链幅值变化范围，从理论上分析十八区段DTC系统的性能。文中给出了相同条件下传统DTC和十八区段DTC方式的转速曲线、定子磁链轨迹、转矩曲线和定子电流波形，实验结果表明十八区段DTC方法能够有效的减小磁链和转矩脉动，提高电流正弦性，改善系统控制性能。

[1] ZHONG L，RAHMAN M F，HU Y W，et al．A direct torque controller for permanent magnet synchronous motor drives[J]．IEEE Transactions on Energy Conversion，1999，14(3)：637-642．

[2] MOHAMED A R I.A novel direct instantaneous torque and flux control with an ADALINE-based motor model for a high performance DD-PMSM[J].IEEE Transactions on power electronics, 2007,22(5):2042-2049.

[3] 邢岩，王旭，刘岩,等.一种新型永磁同步电机定子磁链观测器[J].东北大学学报(自然科学版)，2013，34(6)：766-769.

[4] ANDTEESCU G D，PITIC C I，BLAABJERG F，et al.Combined flux observer with signal injection enhancement for wide speed range sensorless direct torque control of ipmsm drives[J].IEEE Transactions on Energy Conversion，2008，23(2) ：393-402.

[5] TAKAHASHI I，NOGUCHI T.A new quick-response and high-efficiency control strategy of an induction motor[J].IEEE Transactions on Industry Applications，1986，22(5)：820-827.

[6] YAMAMOTO Y,YOSHIDA Y,ASHIKAGA T.Sensorless control of PM motor using full order flux observer[J].IEEE Transactions on Industry Applications,2004,124(8):743-749.

[7] 王旭，邢岩，刘岩,等.永磁同步电机无速度传感器直接转矩控制系统研究[J].东北大学学报(自然科学版)，2012，33(5)：618-621.

[8] RAHMAN M F，HAQUE M E，TANG L，et al.Problems associated with the direct torque control of an interior permanent-magnet synchronous motor drive and their remedies[J].IEEE Transactions on Industry Electronics，2004，51(4)：799-809.

[9] CORLEY M J,LORENZ R D.Rotor position and velocity estimation for permanent magnet synchronous machine at standstill and high speed[C]//Industry Applications Conference.IEEE,1996:36-41.

[10] ZHONG L,RAHMAN M F,HU W Y,et al.Analysis of direct torque control in permanent magnet synchronous motor drives[J].IEEE Trans on power electronics,1997,12(3):528-536.

[11] ZHENG L，FLETCHER J E. A novel direct torque control scheme for a sensorless five-phase induction motor drive[J].IEEE Transactions on Industry Electronics，2007，58(2) ：503-513.

[12] ORTEGA C，ARIAS A.Inproved waveform quality in the direct torque control of matrix-converter-fed PMSM drives[J].IEEE Transactions on Industry Electronics，2007，57(6) ：2101-2110.

High Performance Torque Control of Permanent Magnet Synchronous Motor Based on Eighteen-Section Control

XINGYan1,WANGXu2,YANGDan2,ZHANGZhi-mei2

(1.Tonghua Normal University,Tonghua 134001,China;2.Northeastern University,Shenyang 110819,China)

Traditional direct torque control (DTC) uses six-section circle-flux. The effect of voltage vectors on stator flux is asymmetrical when the stator flux is near the section line, and results in large ripples. When the voltage of stator resistance was considered, the select table of voltage vectors has defect. To deal with the problems mentioned above, the flux formula was deducted in the paper to analyze the performance of stator flux when neglect or consider the voltage of stator resistance, and eighteen-section control method and the improved voltage select table was presented. The performance of these two section control methods was compared. The results prove that the method presented in this paper can decrease flux and torque ripples effectively, besides its simple arithmetic and quickly dynamic-response.

permanent magnet synchronous motor(PMSM); direct torque control; flux and torque ripples; eighteen-section

2016-05-12

吉林省教育厅科学研究计划项目(吉教科合字[2016]244号，245号)

TM341;TM351

A

1004-7018(2017)02-0069-04

邢岩(1986-)，女，博士，讲师。