梁式框支剪力墙结构位移的抗风可靠性分析

黄慎江, 刘海龙

(合肥工业大学 土木与水利工程学院,安徽 合肥 230009)

梁式框支剪力墙结构位移的抗风可靠性分析

黄慎江, 刘海龙

(合肥工业大学 土木与水利工程学院,安徽 合肥 230009)

文章以梁式转换框支剪力墙的顶点位移为研究对象,选择3种转换层及下部与上部若干层的不同等效侧向刚度比和3种不同转换层位置作为影响因素,在《工程结构可靠性设计统一标准》(GB 50153—2008)给出的年最大风压模型的基础上,结合《高层建筑混凝土结构技术规程》(JGJ 3—2010)对等效侧向刚度比、转换层位置以及框支剪力墙顶点位移的规定,得到梁式框支剪力墙顶点位移在最大风压模型下的位移失效概率及其可靠度指标,为梁式转换框支剪力墙在风荷载作用下结构位移的控制提供一种新的思路。

顶点位移;等效刚度比;转换层;失效概率;可靠度

随着国家城镇化的稳步推进以及城市建设用地的日益紧张,具有多重使用功能要求的建筑必然会越来越多,这种建筑结构下部可以布置空间较大的商业、大堂、会议厅、文化娱乐设施,上部楼层可以布置开间较小的住宅、办公用房、酒店等。这种结构形式通常是在转换层上部采用剪力墙结构,转换层及其下部采用落地剪力墙和框支柱构成。不同的功能要求,有不同的转换形式。对国外59栋带转换层的高层调查表明,梁式转换约63%,桁架约27%,其余约占10%[1]；同时由于梁式转换结构具有传力直接、明确、计算方便等优点而被广泛采用。

高层建筑结构在设计中,除了要满足结构承载能力的要求,还要控制结构的位移,使其满足正常使用要求。对高层建筑结构进行位移控制的目的在于[2]:① 避免填充墙和装修破坏以及电梯轨道的变形;② 避免主体结构出现大的裂缝,甚至损坏;③ 避免结构引起附加内力效应;④ 使结构具有足够的刚度避免结构的运动让居住者产生不舒服的感觉[3]。影响建筑结构位移的主要因素是地震作用、风荷载作用和结构的抗侧刚度。由于《建筑结构荷载规范》[4]没有明确提出风荷载位移的可靠性概念,因此对于风荷载作用下的高层抗风设计具有十分重要的意义。严格地说,风荷载的可靠性分析是动力可靠性分析,但是考虑到实际的应用,可以近似地把动力可靠性分析转化为静力分析问题,可按照统一标准在“静风压”作用下按静力可靠度分析方法进行分析[5]。

1 相关规定

带转换层的高层建筑结构,由于转换层下部采用大空间、大柱网的结构形式,结构的层高较高,底部刚度相对于上部剪力墙结构刚度小,容易在转换层处发生刚度突变,进而产生较大的内力和变形,不利于结构的抗震。因此我国《高层建筑混凝土结构技术规程》[6](以下简称《高规》)采用转换层及下部结构与上部若干层的等效侧向刚度比来控制转换层处刚度突变的程度进行平滑的过度。根据文献[6]规定,当转换层设置在第2层以上时,转换层下部与上部的等效侧向刚度比re宜接近于1,非抗震设计时不应小于0.5,抗震设计时不应小于0.8。计算公式为:

(1)

其中,Δ1为转换层及其下部结构的顶部在单位水平力的作用下的侧向位移;Δ2为转换层上部若干层顶部在单位水平力作用下的位移;H1、H2分别为转换层及其下部的高度、转换层上部若干层的高度,两者宜接近且H1≥H2。

《高规》对转换层的位置做出如下规定:8度时,不宜超过3层,7度时不宜超过5层,6度时,可适当提高;对高度在150 m以下的高层建筑结构按弹性方法计算的风荷载标准值作用下的顶点弹性水平位移限值[U/H]和层间最大水平位移限值[Δu/h],无论是部分框支剪力墙,还是除框架外转换层,均为1/1 000。

根据文献[4]，对于风荷载比较敏感的高层建筑物(高度大于60 m),其基本风压应该乘以系数1.1。

2 顶点位移概率分布函数推导

首先做如下假定:① 风荷载在框支剪力墙上的分布形式采用梯形分布;② 按弹性理论方法计算和分析;③ 不考虑结构的扭转。

根据《高规》,沿高度变化的风荷载标准值Wik为:

(2)

则沿各楼层节点的水平集中风荷载标准值Fik为:

(3)

进而可以推出第i楼层(i=1,2,…,n)的剪力为:

(4)

每一层的层间位移Δi、层间位移角θi和顶点位移Δm为:

(5)

(6)

(7)

将(2)～(5)式带入(7)式可以得到框支剪力墙结构顶点的位移为:

(8)

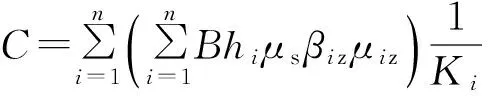
(9)

(2)～(8)式中,i为楼层数;μs为风荷载体型系数;βiz为i处风振系数;μiz为i处风压高度变化系数;B为结构水平宽度;hi为楼层节点处上下层高的1/2之和;hi′为楼层的层高;Ki为第i层抗侧刚度;W0为年最大风压。

不计风向,W0服从极值Ⅰ分布[7]:

(10)

其均值和标准差分别为:

(11)

其中,w0为基本风压。

对于高层结构的顶点位移,可以近似认为服从极值Ⅰ分布[8],因此框支剪力墙的顶点位移也近似认为服从极值Ⅰ分布:

(12)

(13)

对于系数C的概率分布和统计参数很难得到,在结构初步设计时可以近似认为是确定的。进而得到:

(14)

把(11)式带入(14)式即可得到年最大风压的平均值和方差,继而可以得到框支剪力墙结构顶点位移的功能函数和失效概率[9]:

(15)

其中,[Δm]为顶点位移规定限值。进一步可得到可靠度指标β。

3 梁式框支剪力墙算例分析

3.1 等效侧向刚度比和转换层位置的选取

本算例依据《高规》,等效侧向刚度比的取值分别为0.88、1.22、1.55;转换层的位置分别取在第3层、第5层、第7层。当等效侧向刚度比不变时,转换层的位置依次从第3层增加到第7层。因此,该算例共有9种分析情况。同时,等效侧向刚度比的大小,通过落地剪力墙的厚度、上部剪力墙的厚度和肢长来调整,结构的总层数保持不变。

3.2 算例基本信息

某钢筋混凝土框支剪力墙结构,总共39层,总高度121.5 m,转换层位于第3层,采用梁式转换,转换层及下部框支层梁柱的混凝土强度等级为C40,转换层以上为C35,转换层及框支层的层高为4.5 m,上部剪力墙的层高为3.0 m,其中框支柱的截面尺寸为1 400 mm×1 400 mm,转换梁的截面尺寸为1 200 mm×1 400 mm,落地剪力墙的厚度为400 mm,转换层上部剪力墙的厚度为200 mm,楼板厚度为150 mm,转换层楼板厚度为250 mm,框支层的楼板厚度为200 mm。

基本风压为0.45 kN/m2,地面粗糙度为B类。其转换层及框支层的平面图形如图1所示,转换层上部剪力墙结构如图2所示。

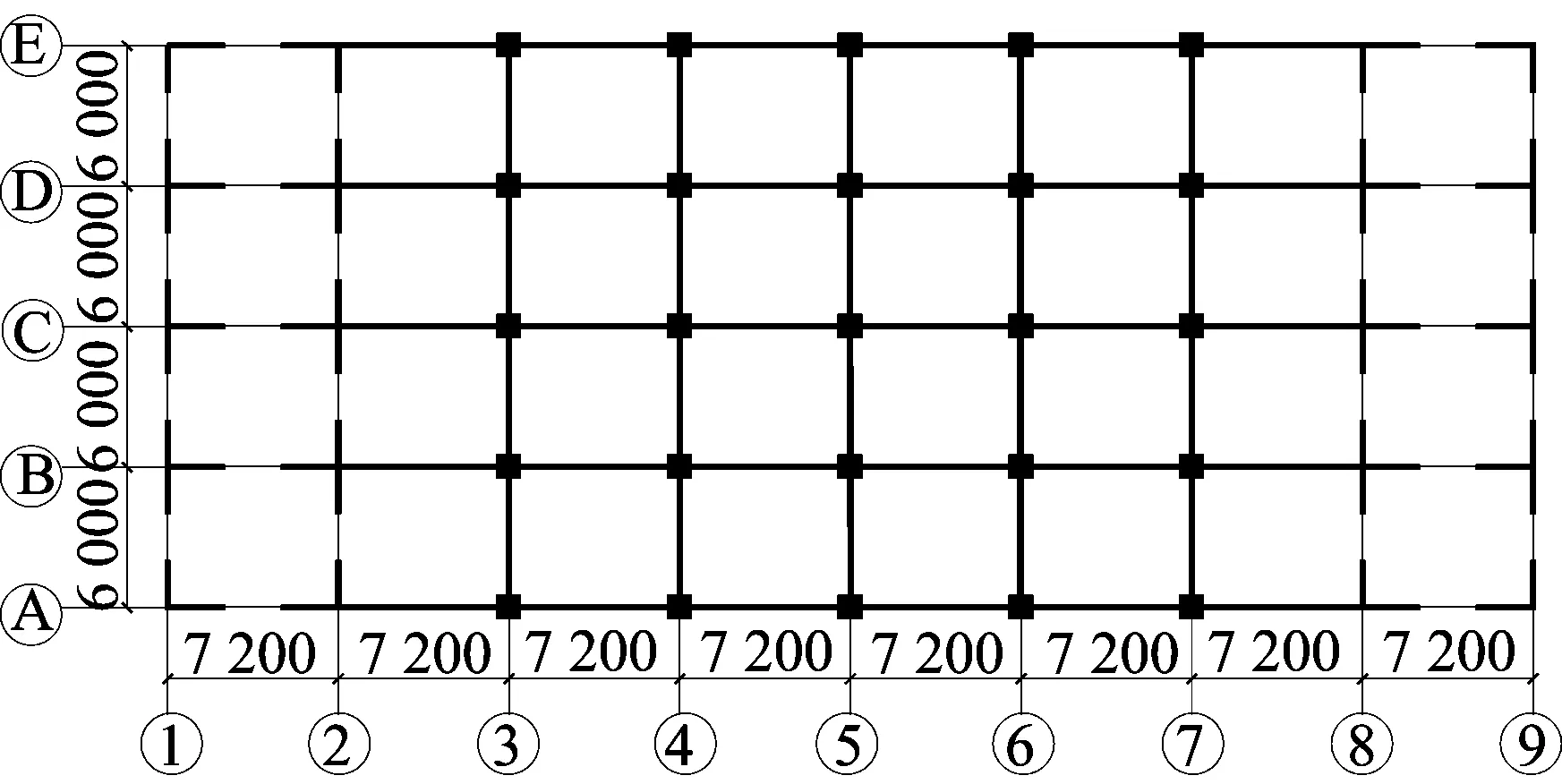
图1 转换层及下部平面布置图

图2 转换层上部结构平面布置图

3.3y方向位移角和位移分析

以y方向的位移角和位移为例,可以得到各个等效侧向刚度比下的层间位移角,如图3所示。

图3 不同re下转换层处的层间位移角

从图3可以看出层间位移角都满足《高规》规定,且先增大后减小,在转换层处发生突变。当re不变时,随着转换层的升高,层间位移角的突变程度相似。当转换层位置不变时,随着re增大,层间位移角逐渐减小,这是因为结构的绝对刚度增大。最大层间位移角的大小和所在楼层位置见表1所列。由表1可以看出,在转换层位置不变时,随着re的增大,最大层间位移角的位置不发生改变。当re不变时,随着转换层位置的升高,最大层间位移角的位置逐渐升高。

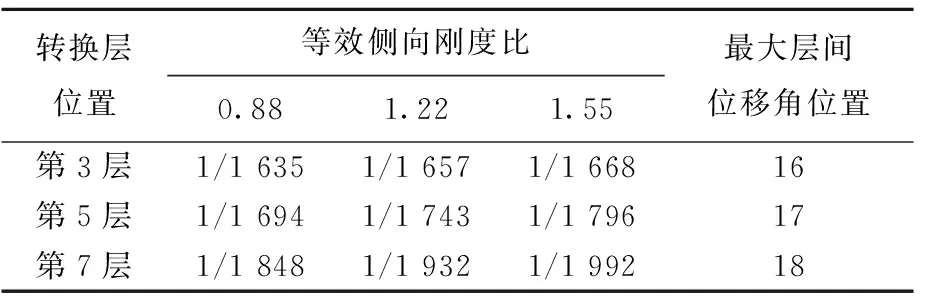
表1 最大层间位移角和转换层位置

y方向各个楼层的位移如图4所示。

图4 不同re下转换层处的结构位移

从图4可以看出,各个楼层的最大位移均发生在顶点。在等效侧向刚度比不变的情况下,随着转换层位置的升高,结构的位移在逐渐减小,这是因为,随着转换层位置的升高,为了保持等效侧向刚度比不变,增大了落地剪力墙的厚度,使结构的绝对刚度增大,同时风荷载作为一种外荷载,变化不大,所以结构的位移变小。在转换层位置不变的情况下,随着等效侧向刚度比的增大,结构的绝对刚度增大,结构下部对上部的约束作用增大,结构的位移变小。各种状况下结构顶点的位移见表2所列。

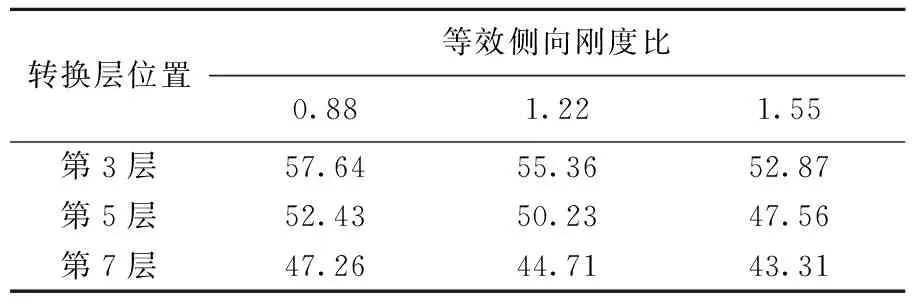
表2 结构顶点位移 mm

从绝对量上看,等效侧向刚度比为0.88、1.22、1.55时,随着转换层位置的升高位移减小的最大值分别为5.21、5.52、5.31 mm,从相对量来看,等效侧向刚度比为0.88、1.22、1.55时,位移减小的最大幅度分别为9.86%、10.99%、10.04%。

当转换层在第3层,等效侧向刚度比从0.88增大到1.55,位移减小的最大绝对量为2.49 mm,最大相对幅度为4.49%;当转换层在第5层时,等效侧向刚度比从0.88增大到1.55时,位移减小的最大绝对量为2.67 mm,最大相对幅度为5.31%;当转换层在第7层时,等效侧向刚度比从0.88增大1.55时,位移减小的最大绝对量为2.55 mm,最大相对幅度为5.39%。

从以上位移减小的绝对量和相对量分析可以看出:当等效侧向刚度比不变时,随着转换层位置的升高,结构顶点位移减小的绝对量和顶点位移减小的最大相对幅度要大于当转换层位置不变时,随着等效侧向刚度比的增大,结构顶点位移减小的绝对量和顶点位移减小的最大相对幅度。这说明了等效侧向刚度比不变时,随着转换层位置的升高,结构整体的绝对刚度要大于转换层位置不变时,随着等效侧向刚度比的增大,结构整体的绝对刚度。虽然框支剪力墙转换层位置的升高,会减小风荷载作用下的位移,但是转换层位置过高,为了使等效侧向刚度比满足要求,就需要增大落地剪力墙的厚度或者数量,影响结构的使用功能要求,同时不利于结构的抗震。

由(2)～(14)式可以计算出不同转换层位置、不同等效侧向刚度比情况下结构顶点位移的失效概率以及可靠度指标,见表3所列。

从表3可知,在年最大风荷载作用下,等效侧向刚度比不变时,随着转换层位置的升高,结构顶点位移的失效概率减小,可靠度指标不断增大,当转换层位置不变时,随着等效侧向刚度比增大时,结构的失效概率减小,可靠度指标增大。

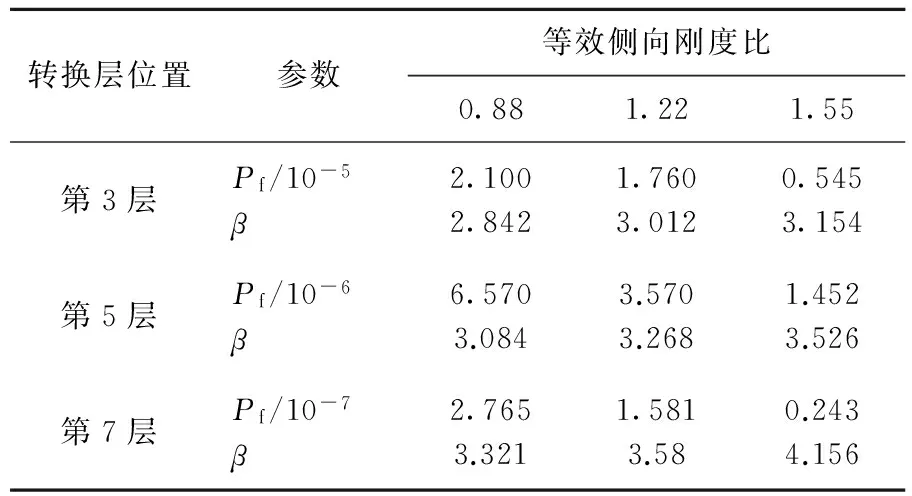
表3 顶点位移的失效概率和可靠度指标

4 结 论

(1) 等效侧向刚度比不变,随着转换位置升高,结构的位移和位移角逐渐减小,且最大位移角的位置随着转换层位置的升高而增大。当转换层位置不变时,随着等效侧向刚度比增大,结构的位移和位移角逐渐减小,但是最大层间位移角的位置不发生改变。

(2) 转换层位置不变时,随着等效侧向刚度比的增大,结构顶点位移逐渐减小,其减小的幅度小于在等效侧向刚度比不变时,随着转换层位置的升高,其位移减小的幅度。

(3) 当转换层位置不变时,随着等效刚度比的增大,结构整体刚度的绝对量小于等效刚度比不变、转换层位置升高时结构整体刚度的绝对量。

(4) 在转换层位置不变时,随着等效刚度比的增大,结构的下部对上部的约束作用增强。结构顶点位移减小,结构顶点位移的失效概率变小,可靠度指标变大。

(5) 在等效侧向刚度比不变时,随着转换层位置的升高,结构刚度的绝对量变大,风荷载作为外荷载变化不大,结构顶点的位移变小,结构顶点位移的失效概率变小,可靠度指标变大。

(6) 框支剪力墙结构在满足转换层下部和上部等效侧向刚度比不变的情况下,可以适当增大转换层的位置,减小风荷载对结构位移的影响。

[1] 黄慎江,凌琦.带高位梁式转换层框架-剪力墙结构体系抗震性能研究[J].合肥工业大学学报(自然科学版),2011,34(8):1232-1236.

[2] 彭伟,李彤梅,葛宇东.高层建筑结构设计原理[M].成都:西南交通大学出版社,2010:6-7.

[3] 方鄂华,钱佳茹,叶列平,等.高层建筑结构设计[M].北京:中国建筑工业出版社,2003:74-75.

[4] 中华人民共和国住房和城乡建设部.建筑结构荷载规范:GB 50009—2012[S].北京:中国建筑工业出版社,2012：30-62.

[5] 董安正.高层建筑结构抗风可靠性分析[D].大连:大连理工大学,2002.

[6] 中国建筑科学研究院.高层建筑混凝土结构技术规程:JGJ 3—2010[S].北京:中国建筑工业出版社,2010：177-178.

[7] 中华人民共和国住房和城乡建设部.工程结构可靠性设计统一标准:GB 50153—2008[S].北京:中国建筑工业出版社,2008：49-50.

[8] 张相庭.高层建筑抗风抗震设计计算[M].上海:同济大学出版社,1997:20-22.

[9] 赵国潘,金伟良,贡金鑫.结构可靠度理论[M].北京:中国建筑工业出版社,2000:12-13.

(责任编辑 张淑艳)

Wind resistance reliability analysis of top displacement of frame-supported shear wall with beam-type transfer

HUANG Shenjiang, LIU Hailong

(School of Civil and Hydraulic Engineering, Hefei University of Technology, Hefei 230009， China)

The top displacement of the frame-supported shear wall with beam-type transfer is studied. In view of three kinds of different equivalent lateral stiffness ratio of transfer storey’s lower and upper structure and three kinds of different transfer storey positions, and on the basis of the annual maximum wind pressure model by the Unified Standard for Reliability Design of Engineering Structures(GB 50153-2008) and the provisions of equivalent lateral stiffness ratio, transfer storey position and top displacement of frame-supported shear wall by the Technical Specification for Concrete Structures of Tall Building(JGJ 3-2010), the top displacement failure probability and the reliability index of the frame-supported shear wall with beam-type transfer under maximum wind pressure model are obtained. The study can provide a new idea for the control of top displacement of the frame-supported shear wall with beam-type transfer under wind load.

top displacement; equivalent stiffness ratio; transfer storey; failure probability； reliability

2015-08-03；

2015-10-19

黄慎江(1964-),男,江苏靖江人,合肥工业大学副教授,硕士生导师.

10.3969/j.issn.1003-5060.2017.02.017

TU318.1

A

1003-5060(2017)02-0225-05