一种基于A*算法的空间多自由度机械臂路径规划方法

宗成星, 陆 亮, 雷新宇, 赵 萍

(合肥工业大学 机械工程学院,安徽 合肥 230009)

一种基于A*算法的空间多自由度机械臂路径规划方法

宗成星, 陆 亮, 雷新宇, 赵 萍

(合肥工业大学 机械工程学院,安徽 合肥 230009)

针对机械臂在运动过程中可能会与工作环境中的障碍物发生碰撞的问题,文章提出了一种基于A*算法的机器人避障路径规划算法。在给定的避障环境下运用A*算法搜索一条给定的自起点到终点的最优避障路径,考虑到机械臂在运动过程中的稳定性,采用二次B样条曲线对该路径进行平滑优化;根据标准的D-H法对机械臂进行建模,建立机械臂的运动学方程,并求取一组能够最优实现避障路径的运动学逆解;检测机械臂本体与障碍物是否发生碰撞,若发生碰撞,结合机器人逆解的多解性,重新选择最优的一组可行解。通过软件Solidworks建立虚拟样机导入ADAMS软件进行仿真实验,最终验证了基于A*算法的空间多自由度机械臂避障路径规划的有效性和可行性。

空间机械臂;A*算法;路径规划;二次B样条;碰撞检测;虚拟样机

路径规划是机器人学领域研究的热点课题之一,对工业机器人的生产制造至关重要。机器人路径规划问题主要解决的是在给定的避障环境下机器人能够自主地搜索一条自起始点到目标点的最优避障路径[1]。为了使机器人能够快速、准确地完成任务,一方面要保证机械臂沿着避障路径平稳地运动,另一方面还要确保机械臂不能与障碍物发生碰撞[2]。目前，已有的二维平面运动路径规划算法技术已不能满足更复杂的工作需要，因此迫切需要一套成熟的三维路径规划算法。文献[3]提出了基于快速扩展随机树(rapidly-exploring random tree,RRT)搜索算法的路径规划,该算法以机器人的起始点作为随机数的根节点,以基准向量作为基准选择节点的扩展方向,通过运动学反解规划全局优化路径；文献[4]提出了基于A*算法变步长搜索的路径规划法；文献[5]提出了一种基于遗传算法的避障路径规划,其针对单个或多个避障物的工作环境,以运动的时间、移动的空间距离以及轨迹长度作为优化指标,在实现避障路径规划的同时进行优化。

本文主要研究的内容如下:

(1) 三维避障路径规划。建立三维坐标下包含障碍物的几何模型,选取合适的算法规划一条自起始点到目标点的最优避障路径,因为考虑到三维空间建模的难度,所以提出了三维环境下A*启发式搜索算法,该算法能够有效快速地对笛卡尔空间中6个方向进行均匀步长搜索,得到一条基于机械臂末端位置的自起始点到目标点的最优避障路径。考虑到机械臂运动的稳定性,利用n次B样条曲线优化搜索的避障路径,以确保机械臂能够稳定地避开障碍物。

(2) 针对上述避障路径,以某具体空间机械臂为例,分析并建立运动学方程,规划基于机械臂末端的轨迹算法。

(3) 碰撞检测。检测机械臂各杆件与障碍物是否发生碰撞，如果发生碰撞,结合机器人逆解的多解性,重新选择最优的一组可行解。

本文最后通过Solidworks建立虚拟样机导入ADAMS软件进行仿真实验,验证了基于A*算法的空间多自由度机械臂避障路径规划的有效性和可行性。

1 场景建模与碰撞检测

1.1 空间机械臂模型

本文研究的空间机械臂是空间开链结构,某工业机械臂平面结构简图如图1所示,其中串联机械臂的运动关节包括移动关节和转动关节。根据其结构特点,将机械臂各杆件碰撞模型简化为长方体模型。

图1 工业机械臂平面结构简图

1.2 障碍物模型

空间障碍物一般都是不规则的几何形状物,为了方便地判断机械臂碰撞问题,必然要对障碍物进行规则化处理。基于空间机械臂的模型,障碍物模型采用长方体包络[1],如图2所示。采用长方体包络障碍物必然会扩大障碍物的区域,但大大简化了碰撞检测方法,对规划出来的路径更具有安全性。

图2 长方体包络检测示意图

1.3 碰撞检测方法

为了解决机械臂整体与障碍物之间的碰撞问题,本文采用了长方体包络检测法,即把机械臂各杆件和障碍物都包络成长方体。假设包络N自由度机械臂各杆件的长方体分别为{R1,R2,…,RN},而包络L个障碍物的长方体分别为{O1,O2,…,OL}。通过对{R1,R2,…,RN}的各条棱边线段与{O1,O2,…,OL}各个面是否有交点的检测,把上述碰撞问题转化为空间直线段与四边形之间的位置关系的判断。

已知空间线段上2个端点p1(x1,y1,z1)和p2(x2,y2,z2)、空间四边形的法向量M=[m1m2m3]以及4个顶点的坐标,由空间解析几何知识可知,直线段与平面位置关系可以用空间直线段方向向量与空间四边形法向量之间的关系判断,其中T=[x2-x1y2-y1z2-z1]。若M·T=0,则直线段与平面平行,没有交点;若M·T≠0,则直线段与平面有交点,设为p0(x0,y0,z0)。判断该交点是否是碰撞点,若是，则必须满足2个条件[3],即交点必须在线段上和交点在四边形内部。障碍物是长方体包络而成,因此前、后面平行于z轴,左、右面平行于y轴,上下面平行于x轴。对平行于x轴的上平面来说,设平面4个顶点为:s1(x3,y3,z3),s2(x4,y4,z3),s3(x5,y5,z5),s4(x6,y6,z6)。

若有:

min(z1,z2)≤z0≤max(z1,z2)，

min(x3,x4)≤x0≤max(x3,x4)，

min(y3,y4)≤y0≤max(y3,y4),

则p0是线段与四边形的交点,其他情况类似。

2 基于A*算法避障搜索路径

2.1A*算法规划路径

A*算法是一种启发式搜索算法,是通过估算函数来实现的,机械臂每走一步都需要计算该函数的值,且该函数值最小的节点也就是机械臂下一步需要到达的位置。启发式函数的一般表达式如下:

(1)

其中,g(n)为机械臂从路径的初始节点到路径规划中的节点n所花费的实际代价;因为机械臂已知从初始节点到节点n实际花费的时间和走过的实际长度,所以函数g(n)值是实际数值;h(n)为从当前节点n到路径规划终点所花费的估算代价;函数F(n)为机械臂在整个路径规划中的总代价。本文中估算函数h(n)为机械臂末端位置与目标节点之间的距离，即

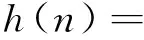
2.2 路径平滑优化

由A*算法均匀步长搜索出的避障路径是一条空间直线段,机械臂在运动过程中会出现抖动,因此采用二次B样条曲线对避障路径进行平滑处理,使得机械臂能够连续稳定地工作。

设有控制顶点D1,D2,…,Dn,则K阶(K-1)次B样条曲线的数学表达式为:

(2)

其中,Ni,k(t)是k-1次B样条曲线的基函数,本文提出的二次B样条曲线每段由3个控制点组成,其基函数矩阵表示为:

3 机械臂规划算法实现

3.1 空间机械臂建模

建模的基本思想为:针对给定的机械臂,1个连杆建立1个坐标系，用齐次变换来描述该坐标系之间的位置与姿态,通过递归的方式得到末端机械臂相对于基坐标系的齐次变换矩阵。建立的第i-1坐标系和第i坐标系之间可以用平移和旋转来实现变换,最后得到相邻坐标之间的变换通式[6],即

其中,θi、αi-1、ai-1、di为相应的连杆参数,即各关节的转角、相邻关节之间的扭转角、连杆长度、相邻关节之间的偏距。

根据D-H法,可以依次计算出相邻坐标系之间的变换矩阵，再顺序右乘即可得到六自由度空间机械臂末端相对于基坐标系的齐次变换矩阵，即

(3)

3.2 机械臂运动学逆解

机器人逆运动学问题,即已知笛卡尔坐标系中机械臂末端位姿矩阵,求机械臂各关节的转角变量。逆运动学求解的问题主要包括3个方面:① 解的存在性,只要保证期望位姿在机械臂的工作空间内即可。② 多解性问题,一般来说,六自由度串联机械臂最多有16组运动学逆解[7-8],逆解的数目取决于机械臂的结构连杆参数里连杆长度和偏距所含非零项的个数;本文研究的机械臂最多有8组运动学逆解,实际上只需要每个关节的1组解。针对该问题,本文选择的方法是结合每个关节的运动范围及“最短行程解”来优化多解问题。③ 求解方法,包括数值解法和封闭解法2类,本文采用封闭解法中的代数解法对机械臂运动学方程进行求解;但是并不是所有的机械臂都能使用该方法,必须在满足Pieper准则[2]的前提下才可以进行代数求解,最后得到所有关节转角变量的数学表达式。

将(3)式进行变换可得:

(4)

由矩阵对应项相等得到12个方程组,求解这些方程组得到8组不同的关节角变量值,然后结合各关节角变化范围及“最短行程”[6]进行优化。如果环境中没有障碍物时,那么采用最短行程原则,即尺寸大的机械臂关节角移动距离少,尺寸小的机械臂关节角移动距离大。如果可行解有多组,那么结合最短行程原则选择1组最优解。

“最短行程原则”优化算法步骤如下：

(1) 已知当前机械臂各个关节角θ1、θ2、θ3、θ4、θ5、θ6。

(2) 通过机械臂运动学逆解得到8组解θn1、θn2、θn3、θn4、θn5、θn6,其中n=1,2,…,8。

(3) 根据机械臂各关节角的变化范围删除部分不可行解,需满足如下关系,即

(4) 再根据“最短行程原则”优化步骤(3)中的机械臂各关节角的解集,得到1组最优解,即

3.3 机械臂避障路径规划算法

(1) 初始化机械臂的起始点、终止点以及每个关节的初始关节角,在三维空间中建立障碍物模型。

(2) 三维路径规划。采用A*算法在给定的三维空间6个方向进行搜索,得到一条基于机械臂末端位姿的、自起点到终点的最优避障路径。为确保机械臂平稳地工作,提取获得的路径数据信息,采用二次B样条曲线对该路径进行平滑处理。

(3) 机械臂运动学逆解。将步骤(2)中得到的三维路径带入Matlab中编写逆解函数进行运动学反解。如果反解失败,那么该点不在机械臂末端执行器工作空间范围内,返回步骤(2)。

(4) 机械臂运动学正解。规划路径上的每个点逆解之后都将得到8组不同的关节角,将最优的1组关节角带入机器人正运动学方程,并得到每个关节的空间坐标。

(5) 碰撞检测。由步骤(4)得到的各关节的空间坐标可以确定具体机械臂相邻两关节间的线段方程,检测机械臂与障碍物间的碰撞情况。若发生碰撞,则返回步骤(4)结合机器人逆解的多解性,在其他几组解中重新选择1组可行解；反之,该解为最优的1组关节角度。

4 仿真结果分析

本文仿真试验的空间机械臂是以工业上最常用的PUMA560型机器人为研究对象。利用标准的D-H法[6]对机械臂进行数学建模,各关节坐标如图3所示,得到的D-H参数见表1所列。

图3 采用D-H表示的PUMA560机械臂关节坐标 表1 六自由度的D-H参数

θi/(°)αi-1/(°)ai-1/cmdi/cm关节变量范围/(°)θ1000-160～160θ2-900d2-225～45θ30a20-45～225θ4-90a3d4-110～170θ59000-100～100θ6-9000-266～266

设置机械臂的D-H参数为：a2=4,a3=1,d2=3,d4=4;初始关节角θ1=90°,θ2=0°,θ3=-90°,θ4=0°,θ5=0°,θ6=0°。仿真实验是在5 cm×5 cm×5 cm的空间里进行的,障碍物是长、宽、高均为2 mm的长方体,其中任取工作空间的点(1,5,3)为起点,点(5,1,2)为终点,A*算法的搜索步长为1,算法搜索的最优避障路径结果如图4所示。采用二次B样条曲线对A*算法搜索的最优避障路径进行优化,其中A*算法搜索的直线段由10个点组成,即

D0(1,5,3);D1(1,5,2);D2(2,5,2);D3(2,4,2);

D4(3,4,2);D5(4,4,2);D6(5,4,2);D7(5,3,2);

D8(5,2,2);D9(5,1,2)。

每段二次B样条曲线由3个相邻的控制点组成,则10个点构成的8段二次B样条曲线仿真结果如图5所示。

图4 A*算法搜索的最优避障路径规划

图5 二次B样条优化的避障路径规划

将末端位置的轨迹方程结合机器人逆运动学方程,求解出每个关节的关节角度,并把最后一个关节的关节角导入ADAMS中生成样条曲线spline-1,在末端位置添加一个旋转驱动,定义为AKISPLZ(time,0,spline-1,0)[9]。在ADAMS中对PUMA560进行运动仿真,可以看到机器人按照给定的要求运动,当杆件之间有干涉运动时,系统会自动报错并停止,结果如图6和图7所示。

图6 机械臂工作仿真模型

图7 机械臂末端位置避障路径规划仿真模型

5 结 论

本文针对空间多自由度机械臂三维路径规划问题,提出并实现了在三维空间内基于A*算法的轨迹避障方法,同时考虑机械臂运动的平稳性,得到了一条自起始点到目标点的最优避障路径。ADAMS仿真结果验证了该方法下机械臂本体在运动过程中能够避开所有障碍物,因此,本文方法对机械臂避障路径规划具有可行性和有效性。

[1] KENNEDY J,EBERHART R C.Particle swarm optimization[C]//Proceedings of IEEE International Conference on Neuarl Networks.Perth:IEEE，1995:1942-1948.

[2] 熊有伦.机器人技术基础[M].武汉：华中科技大学出版社,1996.

[3] 代彦辉,梁艳阳,谢钢,等.基于RRT搜索算法的六自由度机械臂避障路径规划[J].工业控制与应用,2012,31(10):31-37.

[4] 汪首坤,邸智,王军政,等.基于A*改进算法的机械臂避障路径规划[J].北京理工大学学报,2011,31(11):1302-1306.

[5] 韩涛,吴怀宇,杜钊君,等.基于遗传算法的机械臂实时避障路径规划研究[J].计算机应用研究,2013,30(5):1373-1376.

[6] 蔡自兴,谢斌.机器人学[M].北京:清华大学出版社,2000,59-65.

[7] MANOCHA D,CANNY J F.Efficient inverse kinematics for general 6R manipulators[J].IEEE Transaction on Robotics and Automation,1945,5(9):648-657.

[8] TEVATIA G,SCHAAL S.Inverse kinematics for humanoid robots[C]//IEEE International Conference on Robotics and Automation.NJ,USA:IEEE,2000:294-299.

[9] 李增刚.ADAMS入门详解与实例[M].北京:国防工业出版社,2006:191-193.

(责任编辑 胡亚敏)

A path planning approach for multi-DOF spatial manipulator via A*algorithm

ZONG Chengxing, LU Liang, LEI Xinyu, ZHAO Ping

(School of Mechanical Engineering, Hefei University of Technology, Hefei 230009, China)

A novel approach for path planning of spatial serial robot manipulator based on A*algorithm is proposed, seeking to solve the problem that the manipulator might collide with the obstacles in the work space. Firstly, the optimal obstacle avoidance path from a given start point to the end point is obtained by using A*algorithm in a given obstacle avoidance space, and then quadratic B-spline curve is used to smooth the path so as to ensure the stability of the motion. Secondly, the manipulator is modeled and analyzed with standard D-H method, the kinematics equations are built up and a group of optimal inverse kinematic solutions to realize the path are obtained. Finally, this approach detects whether there is a collision between robot and the obstacles, and if there is, then the alternative optimal solution is chosen within the multiple solutions of the inverse kinematics. The result of simulation experiment which introduces the virtual prototype established by Solidworks into ADAMS verifies the effectiveness and feasibility of the proposed path planning approach for multi-DOF spatial manipulator to avoid obstacle.

spatial manipulator; A*algorithm; path planning; quadratic B-spline; collision detection; virtual prototype

2015-10-14；

2016-01-10

国家自然科学基金资助项目(51405128);安徽省自然科学基金资助项目(1508085QE82)

宗成星(1991-),男,安徽宣城人,合肥工业大学硕士生； 赵 萍(1988-),女,山东烟台人,博士,合肥工业大学副教授,硕士生导师.

10.3969/j.issn.1003-5060.2017.02.005

TP391.9

A

1003-5060(2017)02-0164-05