融合Gabor特征的SFM算法三维人脸建模

吴从中, 张凌华, 詹 曙

(合肥工业大学 计算机与信息学院,安徽 合肥 230009)

融合Gabor特征的SFM算法三维人脸建模

吴从中, 张凌华, 詹 曙

(合肥工业大学 计算机与信息学院,安徽 合肥 230009)

采用运动恢复结构(structure from motion,SFM)算法进行三维人脸建模一直以来受到研究者的关注,但其对错误的匹配点比较敏感,因此，文章提出了一种融合Gabor特征的SFM算法三维人脸建模方法。该方法利用Gabor滤波器提取纹理特征,判别轮廓特征点匹配的准确性;针对图像数增多,传统因子分解法不易修正旋转矩阵的问题,利用旋转矩阵的性质求得修正矩阵,避开方程组的求解;提出引入迭代最近点算法将稀疏三维特征点与三维模型进行配准,缩小空间距离,并结合薄板样条函数插值生成特定的三维人脸模型,为增强真实感,进行纹理映射。实验结果表明，该方法有效提高了匹配点的准确性,能够重建出具有较强真实感的三维人脸。

运动恢复结构(SFM);Gabor滤波器;因子分解;修正矩阵;迭代最近点(ICP)

三维人脸建模技术作为计算机视觉领域的一个重要部分[1],被广泛应用于人脸识别[2-3]、计算机游戏和影视制作等多个领域。文献[4]采用激光扫描仪的方法得到的三维人脸模型数据精度高、速度快,但是对计算机的性能要求比较高;Posdamer等人提出结构光的方法,取得了较好的结果,文献[5-6]对该方法做了进一步的改进,建立一个基于结构光的快速获取系统。图像序列重建的方法可以分为基于3D形变模型(morphable model,MM)的方法[7-9]和基于运动恢复结构(structure from motion,SFM)的方法[10]，前者需要大量的模型参数,一旦找到最优的模型参数,就可以重建出精细的3D人脸模型。然而大量的参数使得计算成本较高,并且参数计算可能陷入局部最小。文献[11]提出了利用压缩感知理论估计三维原型人脸与目标人脸的形状相似性,并根据相似性对原型样本进行筛选并构建相应的形变模型的方法。

基于SFM的三维重建算法[12-14],不需要利用目标形状的先验信息。不考虑面部表情变化的情况下,刚性的SFM算法可以通过分析在不同视点观察到的稀疏人脸2D特征点的序列坐标得到其三维结构信息。该方法不需要优化3D平均人脸的参数,只需准确找到每幅图像上相对应的人脸特征点的坐标。稀疏的点匹配方法[15]大量减少了寻找匹配点的难度,但头部发生一定程度的偏转时,稀疏的特征点也容易发生匹配错误。文献[14]提出采用形状转换矩阵(shape conversion matrix,SCM)方法确定自遮挡时人脸特征点的正确位置。SCM方法采用最小二乘法使观察到的面部特征点更接近真实值。文献[16]采用灰度共生矩阵(gray level co-occurrence matrix, GLCM)方法移除错误的特征点后,再进行3D人脸建模。然而在照片数量比较少,特征点数也相对较少的情况下,缺失特征点对建模会带来一定的影响。

本文提出利用Gabor滤波器提取的纹理特征判断特征点是否匹配,采用运动恢复结构的因子分解法计算稀疏点的三维数据,并根据得到的三维数据将三维人脸模型插值为特定的三维人脸模型。

1 系统组成

本文系统的输入是相机拍摄的中性表情的3幅不同姿态的人脸图像,采用主动外观模型提取人脸特征点,利用局部Gabor纹理特征判断特征点匹配性,并手动寻找正确的匹配点,在SFM算法下获得稀疏的三维数据,迭代最近点配准后用一般三维模型插值成特定人脸稠密模型,并进行纹理映射。

本文三维人脸建模流程如图1所示。

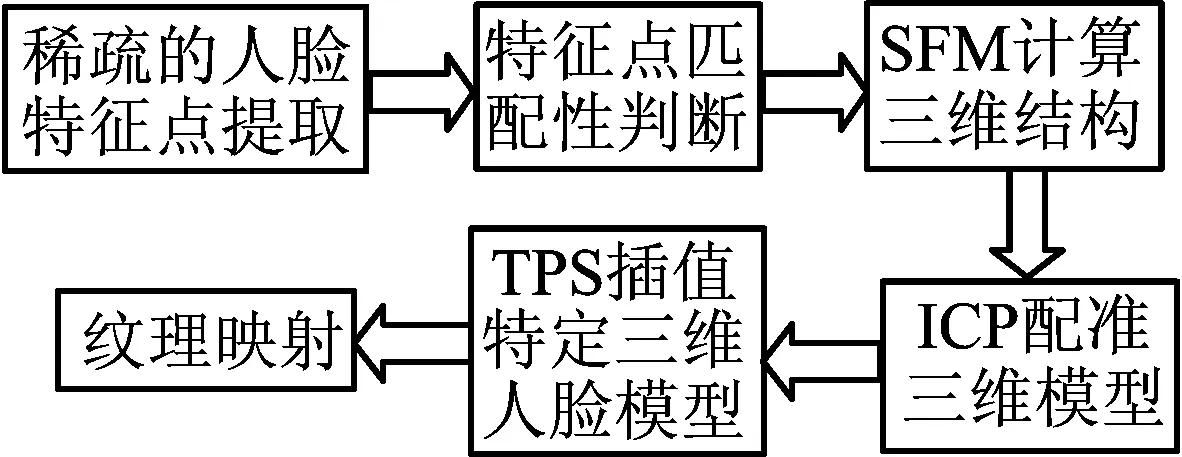
图1 三维人脸建模流程

2 算法描述

2.1 人脸特征点提取

在获得的F幅人脸图像上标定出相同数量的人脸特征点,例如眼睛、鼻子和面部轮廓。这些特征点的标定可以采用手动标定或者利用主动形状模型(active shape model,ASM)[17]和主动外观模型(active appearance model,AAM)等自动特征点检测器标定。本文引用文献[18]的AAM算法获得F幅图像N个人脸特征点的坐标{(xfn,yfn)|f=1,…,F;n=1,…,N}，可得到矩阵W为:

(1)

其中,X、Y均为F×N矩阵,表示所有特征点的xfn、yfn坐标。

2.2 特征点选择

本文利用Gabor滤波器计算脸部轮廓特征点所在图像块的Gabor特征,通过选择有效的特征计算对应图像块之间纹理特征的相关系数,判断特征点的匹配性,并寻找正确的匹配点。因为Gabor小波变换具有与哺乳动物视皮层细胞的刺激响应系统相似的特性,所以通过Gabor滤波器提取的特征具有很好的方向选择性和尺度选择性,并且通过设计合适的Gabor滤波器可以克服不同光照带来的影响[19-20],这是本文选择Gabor特征的原因。

2.2.1 Gabor纹理特征

Gabor函数的定义如下:

(2)

其中,z为坐标(x,y)处的像素值;u和v分别为方向和尺度;波向量ku,v=kveiφu,kv=kmax/fv,φu=πu/8,最大频率kmax=π/2,f为频域核间距因子;σ为窗的宽度与波长的比例。

一幅M×N的图像块I(z),其Gabor特征Gu,v(z)为:

(3)

其中,φu,v(z)为Gabor滤波器。

在实验设置方面,可以选择不同尺寸的Gabor窗、不同的方向和尺度进行实验,以5个尺度v={0,1,2,3,4},8个方向u={0,1,2,3,4,5,6,7}为例。M×N图像块的维度为MN×1,对图像块上每一个像素提取40个特征值,则最终I(z)提取的Gabor特征为MN×40的矩阵。

2.2.1 相似度计算

计算图像块I(z)的有效特征与参考点所在图像块对应的Gabor特征的相关系数,并对其求平均。例如,定义一个相关系数矩阵C∈RF×N,矩阵C中的cij表示第i幅图像、第j点图像块的相关系数,其中cij的公式为:

(4)

其中,li,j为第i幅图像、第j点图像块的纹理矢量;lref,j为参考图像的第j点图像块的纹理矢量;P为有效的相关系数个数。

对于cij中相关系数低的特征点,本文认为它不是正确的匹配点,并进行手动寻找该点的匹配点。

2.3SFM算法

通过矫正匹配点获得人脸特征点坐标W后,采用从运动中恢复结构的因子分解法得到人脸稀疏三维结构[21-22]。W可以分解为:

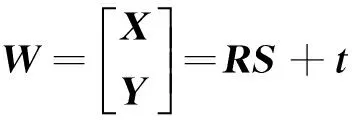
(5)

其中,R为正交投影旋转矩阵;t为平移矩阵;S为人脸三维结构矩阵。

将特征点的中心平移到图像坐标原点,有

(6)

(7)

其中,U为2F×2F阶酉矩阵;D为半正定2F×N阶对角矩阵,并且对角线上的值从大到小排列；V为N×N阶酉矩阵。分别取它们的前三列U2F×3、D3×3和VN×3,则旋转矩阵和结构矩阵的近似解为:

(8)

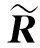
(9)

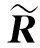
为解决上述问题,本文提出了利用旋转矩阵性质的方法求解每帧的修正矩阵。文献[22-23]中提到的旋转矩阵的性质如下:

对于任意的3×3正交矩阵

当|D|=1时,D中元素c1、c2、c3的求解方法为:

(10)

2.4 稠密三维模型

稀疏的三维数据丢失许多面部细节,因此有必要把稀疏的三维特征点变成稠密的三维数据。本文利用文献[24]提出的薄板样条函数将三维人脸模型对特定人脸的稀疏特征点插值,重建出三维特定人脸稠密模型。

2.4.1 迭代最近点配准

在进行插值之前,本文提出引用迭代最近点(interative closest point,ICP)三维配准的方法[25]对三维模型粗配准,缩小三维模型和参考控制点之间的距离。对空间三维中的2个点集X和Y进行配准,以使目标函数最小,目标函数如下:

(11)

其中,三维模型的点集作为目标点集X,参考点集Y从结构矩阵S中获得,求解得到变换矩阵R和T,使得X和Y满足一定度量准则下的最优匹配。求解步骤为:

(1) 在第k次迭代中计算目标点集X中与Y对应的点Xk,使Dmin=‖Y-Xk‖2。

(2) 计算旋转矩阵Rk和平移矩阵Tk,使得‖RkXk+Tk-Y‖2=min。

(3) 计算Xk+1=RkXk+Tk,Dk+1=‖Y-Xk+1‖2。

(4) 如果Dk+1不小于给定阀值返回到步骤(1),直到小于该阀值时迭代结束,求得变换矩阵。

2.4.2 薄板样条函数插值

薄板样条函数插值的目的是找到一个非线性插值函数F,把ICP配准后的三维模型插值到稀疏特征矩阵Y中,其中函数F为:

F(x)=t+Rx+DTs(x)

(12)

其中,x为3×N的矩阵,为三维模型的控制矩阵;t为平移矩阵;R为旋转矩阵;D为形变参数矩阵;s为薄板样条函数,其表达式为:

(13)

其中，ρ(x)的定义为:

(14)

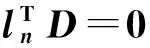
(15)

三维模型上的所有点通过F函数对Y进行插值,便获得稠密的特定三维人脸模型。为了获得具有真实感的三维人脸,将人脸纹理映射到对应的人脸模型上。

3 实验与结果分析

为了证明采用Gabor滤波器提取纹理特征,判断特征点的匹配性对SFM算法重建人脸模型的重要性。本文做了以下2组实验。

实验1 在IMM face database上选取20个人,每人6幅人脸图像,采用AAM提取每幅人脸图像的13个轮廓特征点作为测试点,分别利用Gabor特征、GLCM、局部二值模式(local binary mode,LBP)和Tamura提取测试点和准确点所在5×5图像块的纹理特征,纹理特征相关系数大于0.9则认为是匹配点。它们之间的实验结果对比见表1所列,由表1可以看出Gabor特征判别特征点匹配性更可靠。

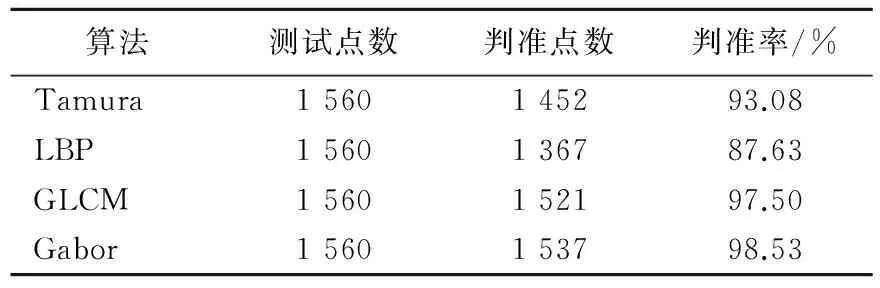
表1 判断轮廓特征点准确度

选取同一人脸的3幅图像,其中正面图像得到的轮廓特征点作为参考点,其他2幅图像(脸部朝左侧为图像1，脸部朝右侧为图像2)轮廓点作为需要验证的点。在每幅图像的轮廓点上都提取它们所在5×5图像块的40个Gabor特征,其中选取图像块的16个有效Gabor特征作相关系数。同一人的轮廓特征点相关系数如图2所示。

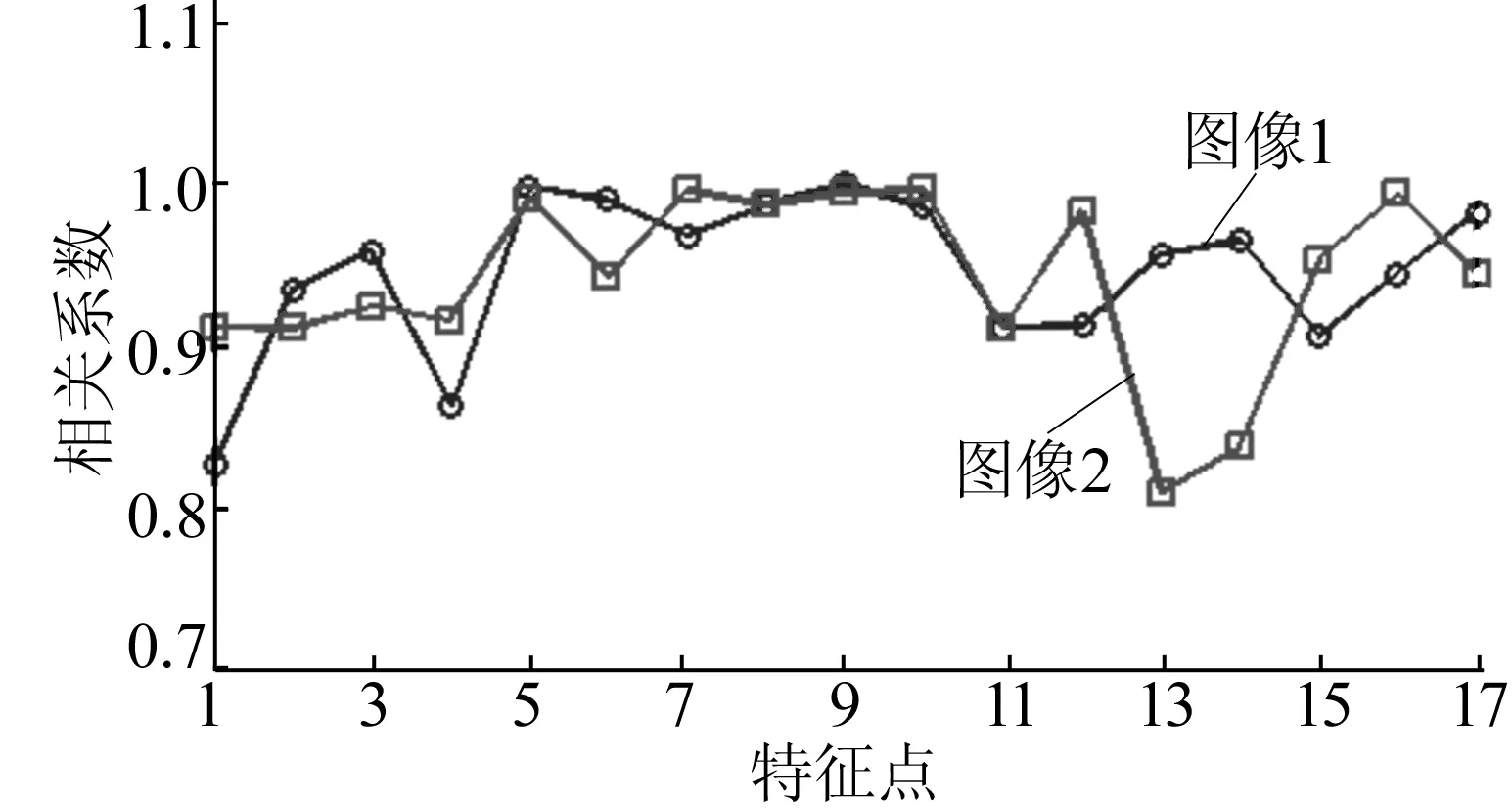
图2 轮廓特征点的相关系数

由图2可以看出,有2个特征点的相关系数低于0.9。对于相关系数小于0.9的点,则认为是不匹配点,并在其周围手动寻找匹配点。

图2的轮廓点未判断特征点匹配性时和修改不匹配的特征点后,两者之间的对比如图3所示。由图3可以看出修改匹配点后,得到的三维数据更准确。

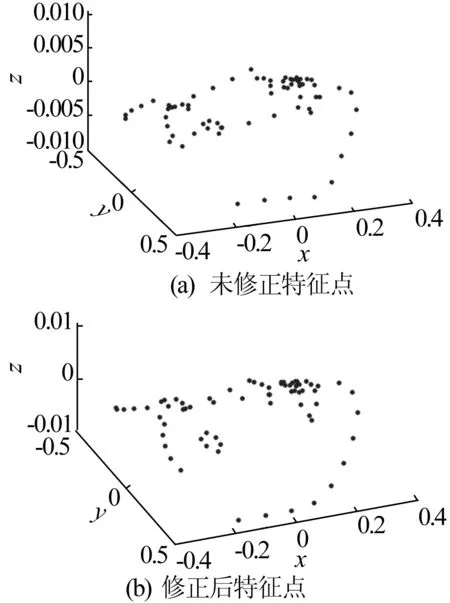
图3 三维稀疏特征点

实验2 ICP配准。X为3 003个点组成的三维人脸模型,Y从结构矩阵S中获得。配准前后的对比结果如图4所示。由图4可以看出,配准后缩小了2个点集之间的空间距离。

图4 ICP配准前后的对比结果

实验结果表明:本文提出的采用Gabor滤波器提取纹理特征,判断特征点匹配性可靠性更高,而且ICP配准后明显缩小了2个空间点集的距离,成为三维人脸建模中不可或缺的一部分。采用每人3幅不同姿态的照片判断特征点匹配性之后重建出来的三维人脸模型如图5所示。直接在通用人脸模型上贴图与在特定人脸模型上贴图的对比如图6所示。

图5 三维人脸重建

图6 模型对比

从图6c可以看出,人脸轮廓的贴图效果更加逼真,由此可知建立特定三维人脸模型对重建三维人脸的重要性以及本文方法的有效性。

4 结 论

本文提出了一种融合Gabor特征的SFM算法三维人脸建模方法。针对特征点不匹配造成SFM算法获得错误三维结构的问题,利用Gabor滤波器提取的纹理特征判断特征点的匹配性,可以有效地降低错误率;利用旋转矩阵性质的方法求得修正矩阵,避免了因子分解中方程组的求解问题;引用ICP三维配准,减小了空间距离。本文方法的不足是没有考虑表情变化下的三维人脸建模。在以后的工作将会继续研究非刚性SFM算法在三维人脸表情建模和三维人脸识别中的应用。

[1] JENI L A,COHN J F,KANADE T.Dense 3D face alignment from 2D videos in real-time[C]//IEEE International Conference on Automatic Face & Gesture Recognition and Workshops.[S.l.:s.n.],2015:1-8.

[2] BLANZ V,VETTER T.Face recognition based on fitting a 3D morphable model[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2003,25(9):1063-1074.

[3] 汪海波,陈雁翔,李艳秋.基于主成分分析和Softmax 回归模型的人脸识别方法[J].合肥工业大学学报(自然科学版),2015,38(6):759-763.

[4] LEE Y C,TERZOPOUIOS D,WAITERS K.ReaIistic modeIing for faciaI animation[C]//Proceedings of the SIGGRAPH95.Los Angeles:[s.n.],l995:55-62.

[5] BEUMIER C,ACHEROY M.3D facial surface acquisition by structured light[C]//International Workshop on Synthetic-Natural Hybrid Coding and Three Dimensional Imaging.Santorini:[s.n.],1999:103-106.

[6] 徐成华,王蕴红,谭铁牛.三维人脸建模与应用[J].中国图象图形学报,2004,9(8):893-903.

[7] BLANZ V,VETTER T.A morphable model for the synthesis of 3D faces[C]//Proceedings of SIGGRAPH 99.Los Angeles:[s.n.],1999:187-194.

[8] 王成章,尹宝才,孙艳丰,等.改进的基于形变模型的三维人脸建模方法[J].自动化学报,2007,33(3):232-239.

[9] ZHU Xiangyu,YAN Junjie,YI Dong,et al.Discriminative 3D morphable model fitting[C]//IEEE International Conference and Workshops on Automatic Face and Gesture Recognition.[S.l.]:IEEE,2015:1-8.

[10] ZHANG P B,HUNG Y S.Non-rigid structure from motion through estimation of blend shapes[C]//The International Conference on Digital Image Computing:Techniques and Applications(DICTA).[S.l.]:IEEE,2015:1-7.

[11] 周大可,吴子扬,杨欣.基于压缩感知理论的3维人脸快速重建[J].中国图象图形学报,2014,19(6):924-931.

[12] 王琨,郑南宁.基于SFM算法的三维人脸模型重建[J].计算机学报,2005,28(6):1048-1053.

[13] 张剑.融合SFM 和动态纹理映射的视频流3维表情重建[J].计算机辅助设计与图形学学报,2010,22 (6):949-958.

[14] LEE S J,PARK K R,KIM J.A SfM-based 3D face reconstruction method robust to self-occlusion by using a shape conversion matrix[J].Pattern Recognition,2011,44(7):1470-1486.

[15] PARK U,JAIN A K.3D model-based face recognition in video[C]//The 2007 International Conference on Advances in Biometrics.Berlin:Springer-Verlag,2007:1085-1094.

[16] YANG Chang,CHEN Jiansheng,XIA Cong,et al.A SFM-based sparse to dense 3D face reconstruction method robust to feature trackong errors[C]//IEEE International Conference on Image Processing.[S.l.:s.n.],2013:3617-3621.

[17] 蒋建国,宣浩.基于MDL 形状模型的医学图像分割[J].合肥工业大学学报(自然科学版),2011,34(4):497-500.

[18] TZIMIROPOULOS G,PANTIC M.Optimization problems for fast AAM fitting in-the-wild[C]//the 2013 IEEE International Conference on Computer Vision.Washington,D.C.:IEEE Computer Society,2013:593-600.

[19] 胡正平,徐波,白洋.Gabor特征集结合判别式字典学习的稀疏表示图像识别[J].中国图象图形学报,2013,18(2):189-194.

[20] DE JONG M A,WOLLSTEIN A,RUFF C,et al.An automatic 3D facial landmarking algorithm using 2D Gabor wavelets[J].IEEE Transactions on Image Processing,2016,25(2):580-588.

[21] TOMASI C,KANADE T.Shape and motion from image stream under orthography:a factorization method[J].International Journal of Computer Vision,1992,9(2):137-154.

[22] 邱少华,文贡坚,回丙伟,等.从运动中恢复目标结构的改进因子分解法[J].中国图象图形学报,2013,18(9):1142-1148.

[23] 王之卓.摄影测量原理[M].武汉:武汉大学出版社,2007:554-555.

[24] PARK U,JAIN A K.3D face reconstruction from stereo video[C]//The 3rd Canadian Conference on Computer and Robot Vision.Washington,D.C.:IEEE Computer Society,2006:41-48.

(责任编辑 闫杏丽)

A method of fusing Gabor features for 3D face modeling by SFM algorithm

WU Congzhong, ZHANG Linghua, ZHAN Shu

(School of Computer and Information, Hefei University of Technology, Hefei 230009, China)

3D face modeling based on structure from motion(SFM) has always attracted researchers’ attention. But it is sensitive to false matching feature points. In this paper, a method of fusing Gabor features for 3D face modeling by SFM algorithm is presented. In this method, texture features extracted by Gabor filter are introduced to evaluate the reliability of outline feature points. With more images, the traditional factorization method is not easy to correct rotation matrix. To solve this problem, the property of a rotation matrix is adopted to calculate corrective matrix. It also avoids solving the equations. Then, sparse 3D feature points and the 3D model are registered by using the iterative closest point(ICP) algorithm to reduce the space distance. And combining the modified 3D model and the shape obtained by thin plate spline interpolation, the person-specific 3D face model can be reconstructed. Finally, the texture is mapped to enhance the realism. The experimental results show that the proposed method is effective in improving the accuracy of matching points and reconstructing higher realistic 3D faces.

structure from motion(SFM); Gabor filter; factorization; corrective matrix; iterative closest point(ICP)

2015-11-23；

2016-03-05

国家自然科学基金资助项目(61371156)；安徽省科技攻关计划资助项目(1401B042019)

吴从中(1965-)，男，安徽安庆人，合肥工业大学副教授，硕士生导师.

10.3969/j.issn.1003-5060.2017.02.008

TP391.41

A

1003-5060(2017)02-0180-06