Peck公式在合肥地铁盾构施工地面变形监测中的适用性分析
2017-04-01徐小马朱大勇卢坤林
徐小马, 朱大勇, 卢坤林
Peck公式在合肥地铁盾构施工地面变形监测中的适用性分析
徐小马1,2, 朱大勇1,2, 卢坤林1,2
(1.合肥工业大学 土木与水利工程学院,安徽 合肥 230009; 2.合肥工业大学 土木工程结构与材料安徽省重点实验室,安徽 合肥 230009)
采用盾构法进行隧道施工,难免会引起地层移动而导致不同程度的沉降,而采用Peck公式进行沉降预测时,首先要利用实测数据对该公式进行验证,并给出适合该地域的计算参数。文章利用合肥轨道交通盾构施工中的地表监测数据对Peck公式进行验证,同时计算出沉降槽宽度参数和地层损失率,为该公式在合肥盾构施工过程中预测地表沉降值提供了依据。
地铁;盾构隧道;Peck公式;地面变形;沉降
从技术原理角度来说,盾构法隧道施工会引起地层移动而导致不同程度的沉降,即使采用先进的土压平衡和泥水平衡式盾构,并辅以盾尾注浆技术,也难以完全防止地面沉降,地面沉降过大对地表建构筑物会产生巨大风险[1]。在众多预测地面变形形态和沉降量的方法中,Peck公式应用最为广泛[2-6]。1969年美国土力学专家Peck教授提出了预测地面变形的公式,该公式是一个经验公式,是基于有限的地区实测资料得到的,在使用该公式时要结合地区特点确定相关参数来对沉降变形进行预测。近年来,我国兴起地铁建设的热潮,各地地铁盾构隧道施工中逐渐积累了一些实测资料,但仍比较零散,也没有形成比较统一的结论[6-7]。我国研究者根据各地盾构施工中公开的资料分析了该公式的适用性,并且给出了初步的建议值[6]。但是我国地域辽阔,各地地质条件差异性很大,很难用统一的参数预测各地盾构施工沉降。很多研究者根据各地的地铁施工沉降数据对Peck公式适用性进行分析,对沉降槽计算方法进行修正[8-11]。各地应利用各自的数据对该公式做适用性分析并给出参数,而目前对于合肥地区的相关研究很少。合肥轨道交通1号线已经完成土建工程,进入铺轨和电气设备安装阶段,3号线也已经开工建设,在盾构施工中积累了很多监测数据。本文结合合肥地区已有的监测数据对该公式在本地区的适应性进行分析并确定相关参数。
1 Peck公式及其适用性检验方法
1.1 Peck公式
Peck在分析大量地表沉降观测数据的基础上,提出了地表沉降槽符合高斯分布的假设,认为地层变形由地层损失引起,施工引起的地面沉降是在不排水的条件下发生的,从而假定地表沉降槽体积等于地层损失体积[2]。其计算公式为:
(1)
其中,s为地面任一点y处的沉降量;smax为地面最大沉降量,位于沉降曲线的对称中心上(对应于隧洞轴线位置,y=0);y为从沉降曲线对称中心到计算点的距离;i为从沉降曲线对称中心到曲线拐点的距离,一般称为“沉降槽宽度”。沉降槽示意图如图1所示。

图1 沉降槽示意图
对于沉降槽宽度的取值,很多研究者给出了不同的方法[7]。目前最常用的是根据文献[3]在伦敦地区的经验,i和隧道深度z0之间存在以下简单的线性关系:
i=Kz0
(2)
其中,K为沉降槽宽度参数,主要取决于土性。对于无黏性土,K值为0.2~0.3;对于硬黏土,K值为0.4~0.5;而对于软的粉质黏土,K值可高达0.7[3]。
定义地层损失率Vl为单位长度的地表沉降槽的断面面积(假设单位长度上的沉降断面一致)占隧道开挖面积的百分比。在不排水条件下,地层损失体积和地面沉降体积应该是相等的。地层损失率Vl与最大位移之间的关系可以通过对(1)式的积分得到[5],设单位长度为1,则有:
(3)
其中
由(3)式可得:
(4)
由(1)式、(2)式及(4)式可得:
(5)
1.2 检验公式适用性的方法
要判断观测数据是否符合Peck公式,并获得相关参数,可以采用如下方法[5]。
(6)
(7)
根据以上方法,可以判别沉降曲线是否符合高斯分布,同时还可以获得相关的拟合参数,包括地层损失率Vl和沉降槽宽度参数K。
2 Peck公式在合肥地区的适用性分析
2.1 合肥轨道交通概况与样本数据获取
合肥轨道交通线路规划[12]及样本来源如图2所示,轨道交通远景线网总长586 km,其中市区线路7条,全长215.3 km;市域线路5条(含1条机场专用线),全长107.2 km。远期中心城区城市轨道交通规划方案由6条城市轨道交通线路组成,共设置了15个轨道交通枢纽。
截止目前,合肥已经动工3条线路。其中1号线施工建设基本结束,即将通车;2号线全线土建施工中;3号线大部分站点开始施工。本文样本数据主要来自合肥轨道交通1、2号线施工和第三方监测数据。
本次验证数据来自1号线土建4标段(图2中区段1)、6标段(图2中区段2)和2号线9标段(图2中区段3)。3个标段分布在合肥市中、南和西北方向3个位置,每隔40~60 m左右取1个监测断面,共计112个样本,尽可能选择周边建筑物少、平坦无堆载的断面,具体位置分布见表1所列。盾构施工时都采用直径6 m的土压平衡和泥水平衡式盾构,并辅以盾尾注浆技术进行施工。
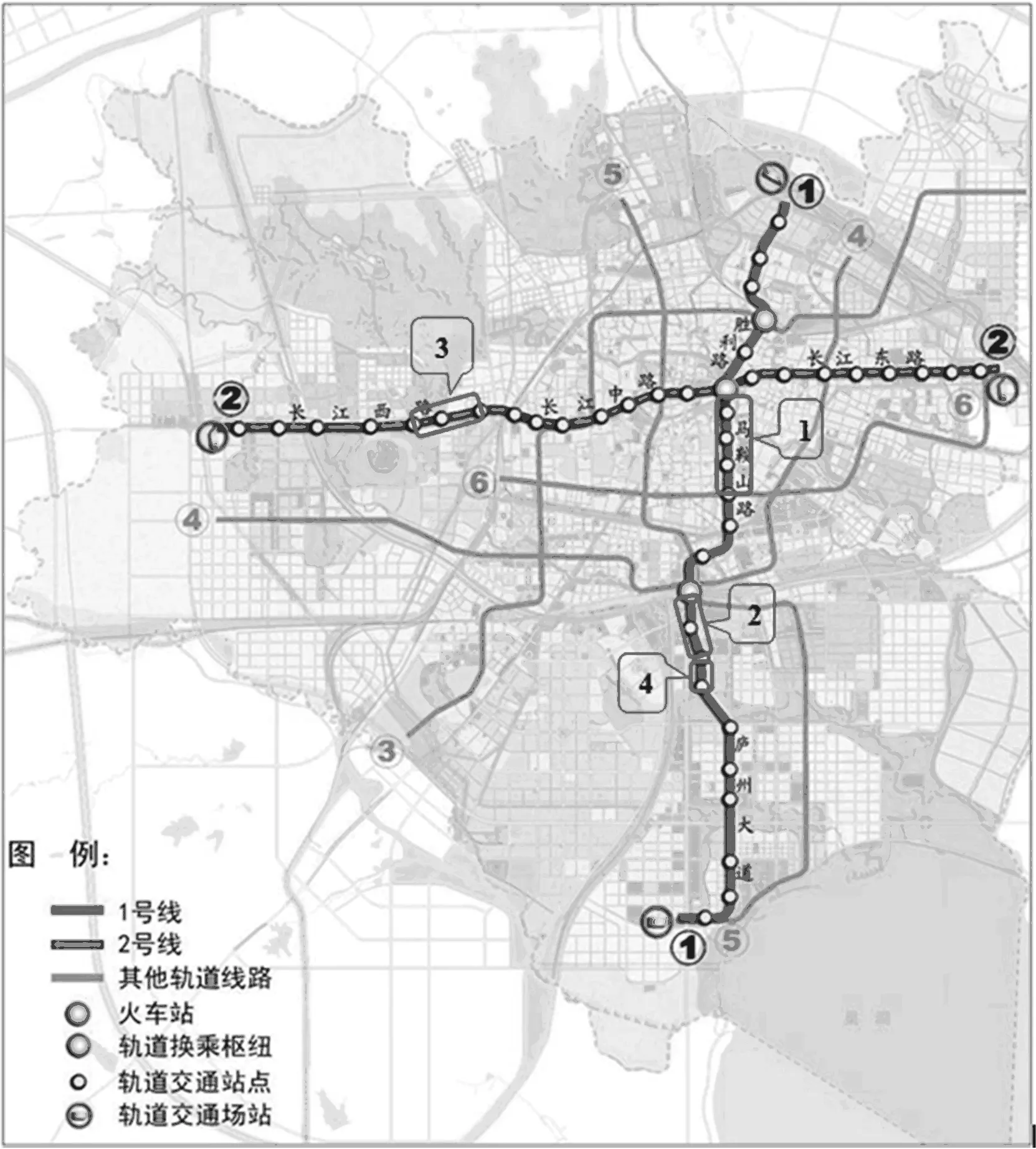
图2 合肥轨道交通线路规划及样本来源 表1 样本数据分布
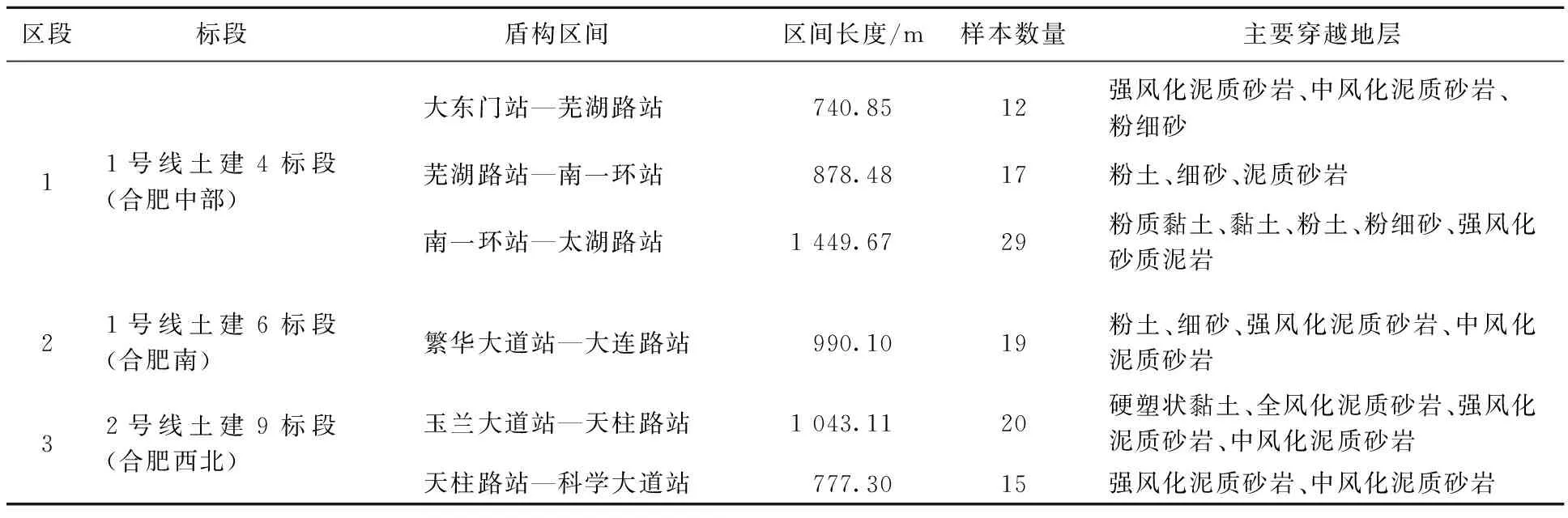
区段标段盾构区间区间长度/m样本数量主要穿越地层11号线土建4标段(合肥中部)大东门站—芜湖路站740.8512强风化泥质砂岩、中风化泥质砂岩、粉细砂芜湖路站—南一环站878.4817粉土、细砂、泥质砂岩南一环站—太湖路站1449.6729粉质黏土、黏土、粉土、粉细砂、强风化砂质泥岩21号线土建6标段(合肥南)繁华大道站—大连路站990.1019粉土、细砂、强风化泥质砂岩、中风化泥质砂岩32号线土建9标段(合肥西北)玉兰大道站—天柱路站1043.1120硬塑状黏土、全风化泥质砂岩、强风化泥质砂岩、中风化泥质砂岩天柱路站—科学大道站777.3015强风化泥质砂岩、中风化泥质砂岩
2.2 适用性分析
按照如下步骤分析判断Peck公式的适用性,并计算相关参数。
(1) 通过实地测量获取监测断面最终沉降量数据。
(3) 若是线性关系,则利用(4)式反算出地层损失率Vl,利用(7)式计算沉降槽宽度i,利用(2)式计算沉降槽宽度参数K。

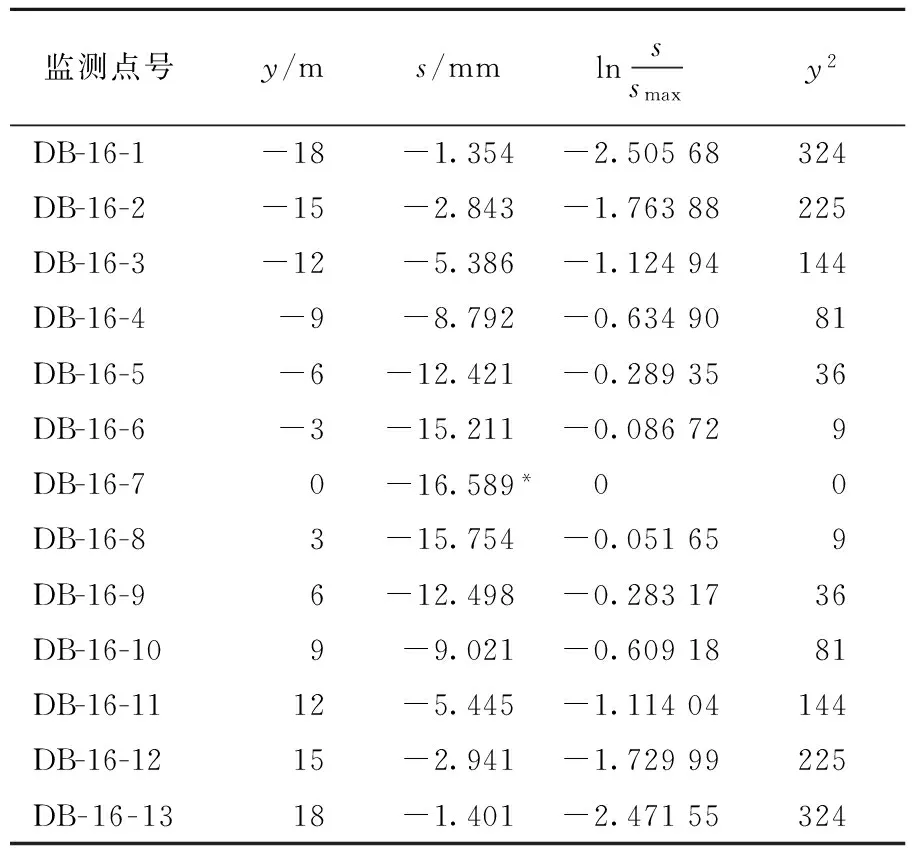
表2 DB-16监测断面沉降数据
注:*数据为DB-16监测断面沉降数据最大值smax。
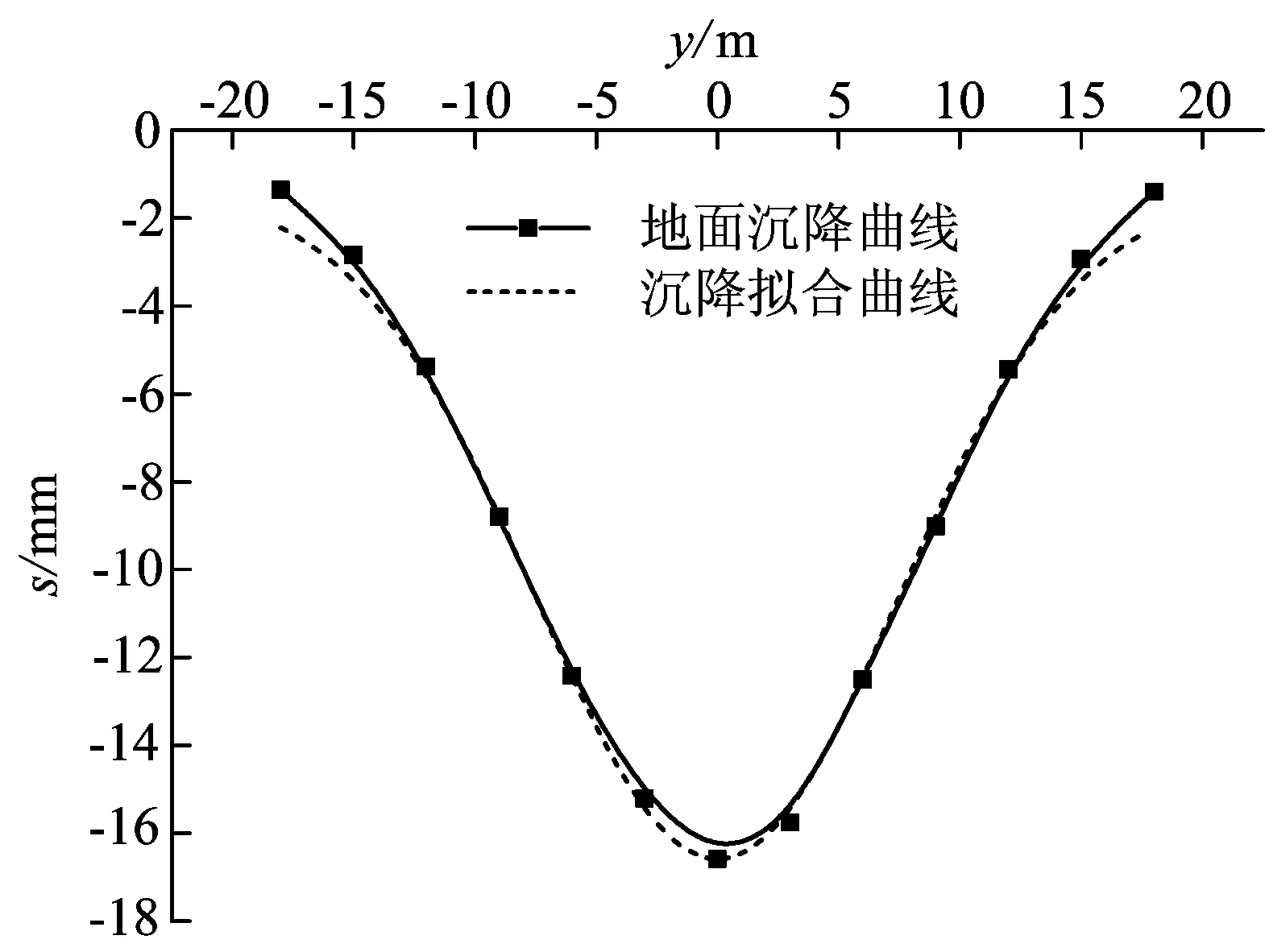
图3 DB-16监测断面沉降曲线

图4 DB-16监测断面关系
从图3可以看出,由DB-16断面监测数据的沉降曲线能较好地拟合成高斯分布。
由上述结果可知,沉降基本满足Peck公式时,“ln(s/smax)-y2”关系的相关系数接近于-1,由于相关文献并未给出具体判断标准,通过分析,本文设定左、右侧拟合相关系数R2≤-0.95时认为沉降满足Peck公式。同样,相关文献也未对满足Peck公式的地表沉降对称性进行相关研究,为了评价沉降左、右对称性的情况,本文引入对称参数C,计算公式为:
(8)
其中,mL、mR为左、右侧拟合斜率。
通过分析认为,当C≤5%时为对称性好;当C≥20%时为无对称性;当5% 2.3 沉降槽宽度参数与地层损失率计算 在表1所列的6个盾构监测区间上共选取112个监测断面的监测数据,按照2.2节DB-16断面数据的处理方法进行计算,共计98个符合高斯分布(R2≤-0.95),占样本数量的87.5%。利用(2)式计算得到沉降槽宽度参数K,在98个数据中有89个在0.5~0.7之间,约占样本数量的91%。 对实测数据分析可知,合肥地铁盾构施工中的地面沉降基本满足高斯分布的规律。K主要分布在0.5~0.7之间,其中穿越地层为粉细砂、中风化泥质砂岩时K在0.5~0.6之间,穿越地层为强风化泥质砂岩时K在0.6~0.7之间。 同样选取以上98个断面利用(4)式反算出地层损失率Vl,有90个数据在0.8%~1.8%之间,占92%。 大东门站—芜湖路站区间12个断面K与Vl计算结果见表3所列。 表3 大东门站—芜湖路站区间监测断面K与Vl计算结果 根据上述统计结果可以确定合肥地区的沉降槽宽度参数K为0.5~0.7,地层损失率Vl为0.8%~1.8%。 下面对正在开挖断面(1号线土建8标段,大连路站—花园大道站区间,图2中区段4)进行地表沉降预测,K取统计结果的中值0.6;Vl取中值1.3%,预测结果见表4所列。 由表4可知,采用监测数据统计得出的K和Vl值作为Peck公式计算参数,能较准确地预测盾构施工中地表沉降量的大小。 表4 Peck公式预测地表沉降结果 本文计算分析了112组监测样本数据,证实了Peck公式适用于合肥轨道交通建设。根据相关公式求解统计出合肥地区的沉降槽宽度参数K的范围为0.5~0.7,建议计算时取0.6;盾构隧道的地层损失率Vl的范围为0.8%~1.8%,建议计算时取1.3%。 为了判断沉降对称性,本文引入对称参数C,能较好地判断出地表沉降的对称情况。在监测过程中仍然有部分数据和预测值相差较大,说明盾构施工受多种因素影响,并且在某些情况下并不可控。下一步研究工作将探寻各种因素和条件对沉降的影响,不断完善Peck公式的适用范围和计算方法。 [1] 应国柱,汪鹏程,朱大勇,等.模糊层次分析法的改进及其在地铁施工风险评估中的应用[J].合肥工业大学学报(自然科学版),2014,37(10):1244-1248. [2] PECK R B.Deep excavations and tunneling in soft ground[C]//Proceedings of the 7th International Conference on Soil Mechanics and Foundation Engineering.Mexico City:[s.n.],1969:225-290. [3] NEW B M,O’REILLY M P.Tunnelling induced ground movements:predicting their magnitude and effects[C]//Proceedings of the 4th International Conference on Ground Movements and Structures.London:Pentech Press,1991:691-697. [4] KNOTHE S.Observations of surface movements under influence of mining and their theoretical interpretation[C]//Proceedings of the European Congress on Ground Movement.[S.l.:s.n.],1957:210-213. [5] ATTEWELL P B,YEATES J,SELBY A R.Soil movements induced by tunnelling and their effects on pipelines and structures[M].Glasgow:Blackie Academic & Professional,1986:10-50. [6] 沈培良,张海波,殷宗泽.上海地区地铁隧道盾构施工地面沉降分析[J].河海大学学报(自然科学版),2003,31(5):556-559. [7] 韩煊,罗文林,李宁.地铁隧道施工引起沉降槽宽度的影响因素[J].地下空间与工程学报,2009,5(6):1188-1193. [8] 刘印,张冬梅,黄宏伟.盾构隧道局部长期渗水对隧道变形及地表沉降的影响分析[J].岩土力学,2013,34(1):290-298. [9] 王如路.上海软土地铁隧道变形影响因素及变形特征分析[J].地下工程与隧道,2009(1):4-9,55. [10] 郭延华,吴龙海.南京地层地铁隧道施工的Peck公式修正[J].河北工程大学学报(自然科学版),2013,30(1):41-44. [11] 姚爱军,赵强,管江,等.基于北京地层地铁隧道施工的Peck公式的改进[J].地下空间与工程学报,2010,6(4):789-793. [12] 合肥城市轨道交通有限公司.合肥市城市轨道交通近期建设规划线路[EB/OL].(2010-07-22)[2015-10-10].http://60.174.200.182:81/plan-info.asp?newid=5. (责任编辑 张淑艳) Applicability analysis of Peck formula in ground deformation monitoring of Hefei metro shield construction XU Xiaoma1,2, ZHU Dayong1,2, LU Kunlin1,2 (1.School of Civil and Hydraulic Engineering, Hefei University of Technology, Hefei 230009, China; 2.Anhui Key Laboratory of Structure and Materials in Civil Engineering, Hefei University of Technology, Hefei 230009, China) The application of shield tunneling method in tunnel construction will inevitably generate the strata movement, which will lead to different degrees of settlement. When using the Peck formula for settlement predication, the formula needs to be verified by the experimental data. And the calculation parameters suitable for the region should be gotten. In this paper, the formula is verified by the surface monitoring data of Hefei metro shield construction. And the trough width parameter and volume loss ratio are calculated. The study provides a basis for the predication of the value of surface settlement in the process of shield construction in Hefei. metro; shield tunnel; Peck formula; ground deformation; settlement 2015-10-30; 2015-11-19 国家自然科学基金资助项目(51179043;41402256);轨道交通建设工程质量安全监督站科研资助项目(2015FFCZ0617) 徐小马(1990-),男,安徽芜湖人,合肥工业大学硕士生; 朱大勇(1965-),男,安徽枞阳人,博士,合肥工业大学教授,博士生导师. 10.3969/j.issn.1003-5060.2017.02.014 TU433 A 1003-5060(2017)02-0210-05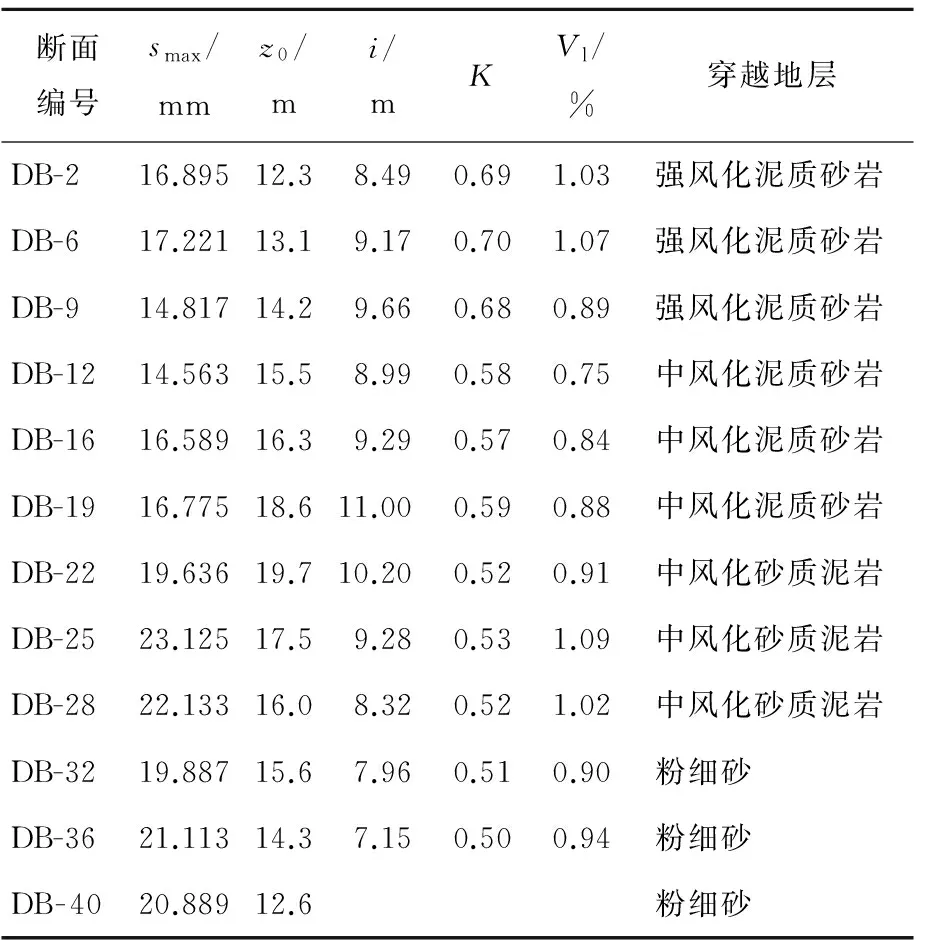
3 Peck公式验证
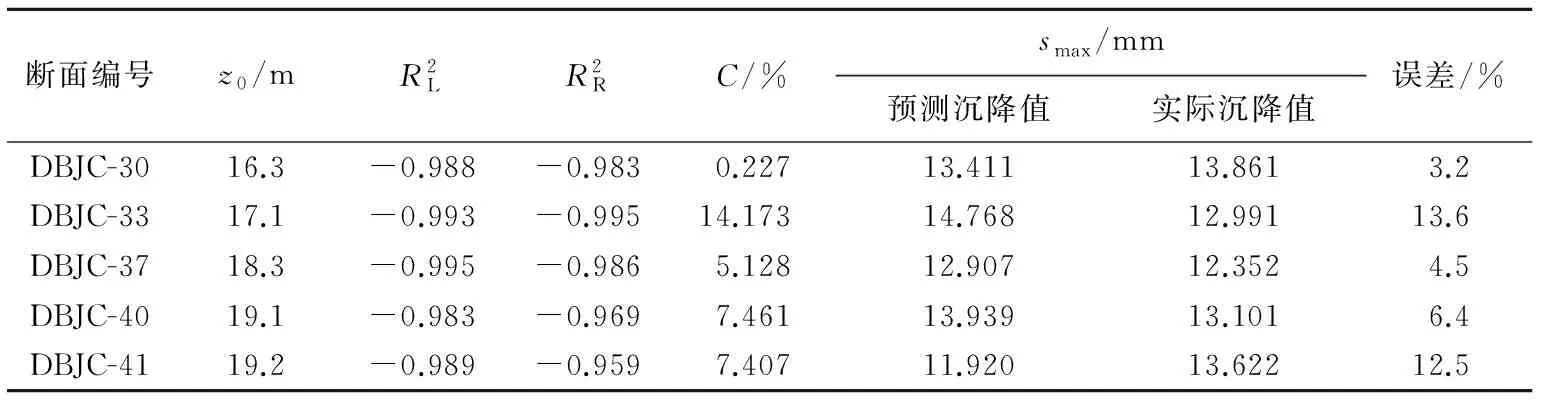
4 结 论
