泥质夹层的三维预测与地质模型的等效粗化表征 <br/>——以加拿大麦凯河油砂储集层为例

泥质夹层的三维预测与地质模型的等效粗化表征
——以加拿大麦凯河油砂储集层为例

2020-05-05尹艳树陈和平黄继新冯文杰刘焱鑫高禹锋

石油勘探与开发 2020年6期

尹艳树，陈和平，黄继新，冯文杰，刘焱鑫，高禹锋

（1. 长江大学地球科学学院，武汉 430100；2. 中国石油勘探开发研究院，北京 100083）

0 引言

薄的泥质夹层对油砂蒸汽辅助重力驱开发（SAGD）具有重要影响，是开发后期剩余油分布的主控因素，如何提高泥质夹层的预测精度是油砂开发面临的重要问题。油砂储集层中薄泥质夹层厚度一般小于20 cm，常规测井曲线难以识别，其横向延展预测更加困难。同时薄泥质夹层地质模型三维表征输出的千万级别的网格数量给油藏数值模拟带来巨大的计算量，往往需要对其进行模型粗化，降低网格数量以适应数值模拟的需要。薄泥质夹层在地质模型网格中所占比例较小，传统粗化方法容易将其过滤掉，所得粗化模型难以体现薄泥质夹层的影响。

泥质夹层对储集层垂向渗透率具有较大影响，Haldorsen 等[1]认为夹层的存在使流线迂曲度增加，进而降低垂向渗透率，提出采用流线方法计算储集层有效垂向渗透率；Begg 等[2-3]基于流线理论框架，将流线方法从二维扩展到三维，但该方法的缺点是将地质模型中的所有细网格等效为一个粗网格；Green 等[4]给出了二维和三维情况下夹层长度和宽度的统计函数表达式，给Begg 等提出的垂向渗透率粗化等效计算提供了统计学解释，但对油藏范围内不同粗化网格内部夹层的追踪和统计未能给出有效解决方案，难以对实际油藏生产预测提供支持；李君等[5]通过计算粗化范围内砂岩连通性实现了渗透率的表征，较好再现了夹层影响下不同方向渗透率值的差异，但该方法通过判断砂岩连通与否来决定网格值是否有效，对有效网格渗透率的粗化计算采用常规的加权平均，未能考虑夹层导致的流体流动路径增加，故粗化后渗透率值误差较大。

本文以加拿大麦凯河油砂丰富的岩心资料为基础，开展泥质夹层延伸范围预测，提出存在夹层时模型粗化过程中渗透率的表征方法，最大限度体现夹层对流体流动的影响，并通过指标对比验证方法的有效性。

1 研究区概况

加拿大麦凯河油砂位于加拿大阿尔伯达省阿斯巴斯卡地区，面积760 km2，预计建产规模200×104t/a。油砂储集层顶面埋深160～180 m，储集层平均净厚度18 m，平均饱和度75%，有效孔隙度约32%，渗透率1～5 μm2，研究区取心井185 口，井距为600～800 m。

据现有研究成果[6-9]，研究区白垩系麦克默里组分为下、中、上3 段，上段（研究目的层段）受潮汐与河流作用影响，砂体以潮汐砂坝和砂坪为主，两侧发育混合坪沉积，弱水动力时期发育泥质物披覆沉积，类似心滩坝中落淤层，后期经潮流作用改造保存不完整。岩心显示上段储集层发育泥质夹层，有少量间断，其产状多为水平状，厚度较薄，多为毫米级；露头剖面显示上段泥质夹层多为水平状，连续性差，延伸距离大多数小于10 m。储集层中频繁发育的泥质夹层渗透率极低，甚至为非渗透层，直接阻碍了油砂SAGD开发中蒸汽腔的发育，严重影响油砂开发效果。

2 泥质夹层三维预测

2.1 基于泥质夹层终止频率的夹层分布预测

泥质夹层对开发存在严重的影响[10-14]，泥质夹层的分布规模可采用露头资料进行预测[15-17]，但因部分泥质夹层只是部分出露，通过露头观察所得泥质夹层长度统计不具有完备性。Geehan 使用几何概率来推断具有无偏性的泥质夹层长度分布，但要求露头是规则方形的，实际露头很难符合条件[18]；White 等[19]提出使用终止频率和埃尔朗模型来计算泥质夹层规模，为泥质夹层规模预测提供了新的方法，该方法认为在露头上的泥质夹层终止情况与实际生活中的排队耗时理论一致。生活中两人排队、一人排队等待另一人到来及等待两人出现的时间间隔等同于在露头剖面上看到泥质夹层终止（露头范围内可以测量泥质夹层长度）、仅看到泥质夹层一端及未能看到泥质夹层终止。通过观察每一条泥质夹层端点出现状况获得其终止频率[19]：

式中nT,i为在有限露头上观察到的第i 个泥质夹层终止的数量（nT,i=0，1 或2）。如果泥质夹层完全穿越工区，则其终止数量为0；如果有一端延伸出工区，则终止数量为1；如果两端均没有延伸出工区，则终止数量是2。

观测到0，1 或2 个终止的概率可以分别用几何概率来计算：

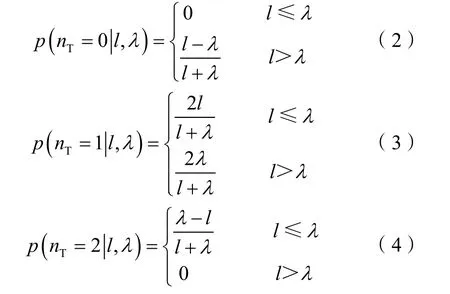
长度为l 的泥质夹层观测终止数量均值为：

将（3）式、（4）式代入（5）式可得到终止端点数量的期望值为：

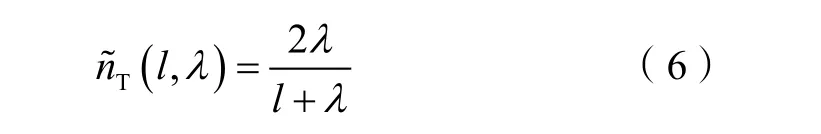
由（6）式可知，如果l 远小于λ，则期望观察到两个端点；如果l 远大于λ，则没有观察到端点；如果l 等于λ，则总是观察到一个端点。

在长度为λ的露头剖面上，观察到长度为l 的泥质夹层的概率为：

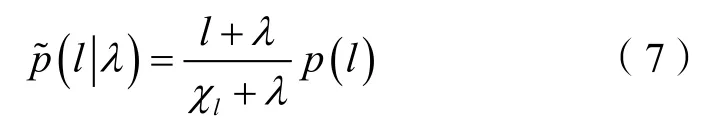
长度为l 的泥质夹层的观测平均终止数量期望值则可以通过下式计算：

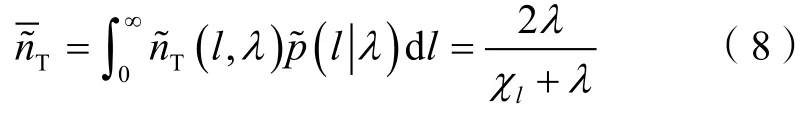
观察到不同端点个数的泥质夹层长度的均值为：

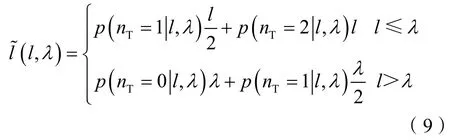
（9）式整理得：

观察到不同端点个数的泥质夹层长度期望值可以通过下式计算：

将（8）式和（11）式带入（1）式，可以获得简化的终止频率计算公式：

以及泥质夹层平均长度计算公式：

因此，只需要统计泥质夹层在岩心上发育的端点数量，就可以计算出泥质夹层的终止频率，进而利用（13）式计算平均延伸长度，实现泥质夹层规模预测。

2.2 麦凯河油砂储集层内泥质夹层分布预测与建模

2.2.1 岩心夹层终止频率统计与夹层规模预测

麦凯河油砂储集层取心井185 口，基本覆盖全区，岩心上泥质夹层连续状态可以认为是对地下储集层中泥质夹层分布情况的抽样观察。因此，可以根据岩心照片上泥质夹层的终止情况预测泥质夹层延伸长度。

对研究区内50 口取心井泥质夹层的端点和长宽进行统计，共识别出5 905 个泥质夹层，其中5 544 个穿越整个岩心筒，即端点为0 的有5 544 个，出现概率为93.9%。端点为1 的泥质夹层253 个，出现概率为4.3%。有2 个端点的泥质夹层108 个，出现概率为1.8%。其中有2 个端点的泥质夹层平均长度约为40 mm，平均厚度约为2 mm，基于终止频率计算的平均长度为0.1 m，与泥质夹层平均长度0.04 m 具有较好的可比性。基于终止频率计算得到厚度2～4 mm 的泥质夹层平均长度为1.19 m；厚度4～8 mm 的泥质夹层平均长度为3.86 m，与露头观察到的泥质夹层平均延伸长度0.87 m较为接近；厚度大于16 mm 的夹层延伸平均长度计算值为45.92 m（见表1）。

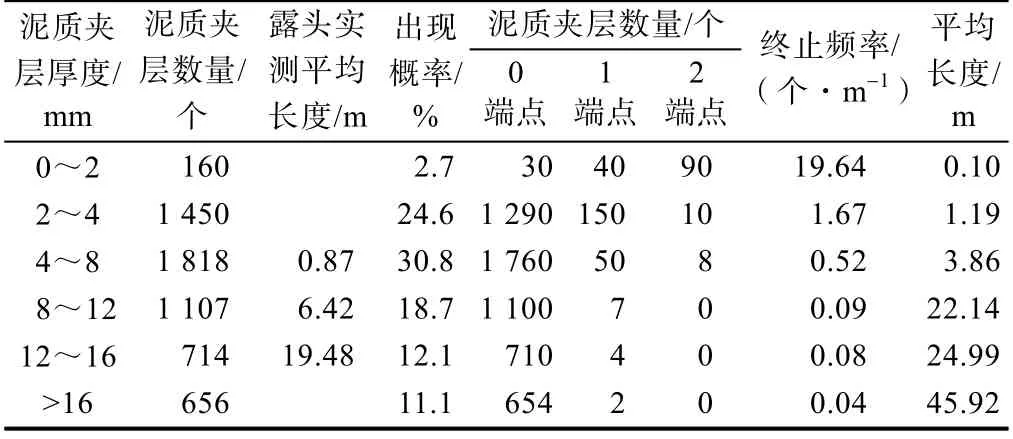
表1 不同厚度泥质夹层端点数、终止频率及平均长度

利用终止频率预测的夹层延伸范围与实际解释成果也具有较好的可比性。Burton 等[20]对犹他州的Sego砂岩进行了露头观察和解释，完全终止的泥质夹层长度分布在0.1～15.0 m，均值为5.0 m，利用终止频率预测的泥质夹层长度在0～45.0 m，均值为16.3 m。本文对麦克默里组倾斜泥质夹层也进行了分布预测，储集层结构精细解剖表明，倾斜泥质夹层延伸距离为37.2～107.0 m，本文方法预测的泥质夹层平均延伸长度为67.8 m。倾斜泥质夹层较本文研究区泥质夹层延伸距离稍长主要是因为倾斜泥质夹层连续性相对较好。由此可见利用岩心观察的终止频率可以用于夹层延伸距离的预测。

将统计的泥质夹层厚度与计算的延伸长度进行回归分析，两者之间呈较为显著的正相关（见图1）。可通过井资料获得的泥质夹层厚度对泥质夹层横向规模进行函数表征。

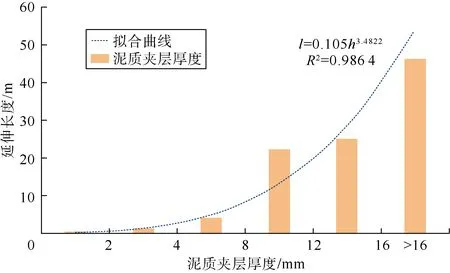
图1 泥质夹层厚度与延伸平均长度关系图

2.2.2 薄夹层三维地质建模

由于泥质夹层近似水平，分布频率大、延伸距离短，其形态可简化为长方体，三维分布可采用示性点建模方法进行预测。示性点过程是一种常用的随机地质建模方法[21-27]，通过点分布函数产生空间点，随后在该点赋予目标体属性（如目标体类型、几何形态等）。当目标体属性百分比达到规定阈值时，不再产生空间点，获得一个模拟实现。研究区广泛连续分布的砂岩中夹杂薄泥质夹层，背景相可设置为砂岩相，随后在砂岩背景中产生薄泥质夹层，模拟终止条件由井统计的泥质夹层百分比进行控制。

建立模型时，根据不同厚度泥质夹层，给予不同的长宽抽样值，例如夹层厚度在8～12 mm 时，选择均匀分布函数，下限为8 mm，上限为12 mm，平均值为10 mm。随机抽样该网格点泥岩厚度，利用图1 建立的泥质夹层厚度与长度关系确定泥岩延伸长度。根据泥质夹层规模，将模拟网格步长设置为5 m×5 m×2 mm，网格总量为343×231×2 100=166 389 300。设置好相关参数，采用目标建模方法实现泥质夹层三维空间分布预测（见图2），所建模型很好地再现了不同厚度泥质夹层的形态和空间分布。整体上，泥质夹层近似水平，规模均较小，发育频率较高，绝大多数泥质夹层仅穿越一口井，井间随机分布大量泥质夹层。

图2 研究区泥质夹层分布三维模型

渗透率模型采用序贯高斯模拟方法，以井解释渗透率值作为参考，泥质夹层处设置为非渗透，完成渗透率模型建立（见图3）。模型整体渗透率值较高，一般超过500×10−3μm2，同时在此背景下，分布有大量泥质夹层局部低渗区。

3 模型等效粗化方法

3.1 迂曲路径计算等效粗化

图3 研究区渗透率分布三维模型

泥质夹层的存在会使流体流动路径发生改变，影响剩余油分布。夹层改变流动路径本质上表现为增加流体穿越该空间的流动长度，等效于微观结构中流体流动迂曲度。因此，将粗化网格作为宏观结构体，而内部夹层则是微观结构，只需要确定流管在夹层约束下的迂曲路径，就可以通过达西公式计算其不同方向的渗透率[1-3]。

对每个流管应用达西定律：

在垂直方向上，总的流量为：

把 jQ 带入（15）式有：

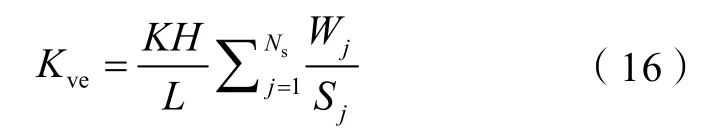
假定每个流管具有相同的截面积，则有：

于是有：

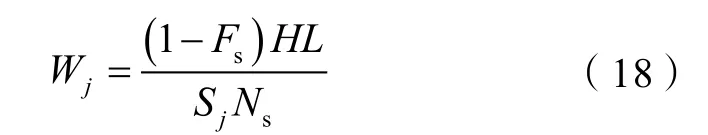
将（18）式带入（16）式，则有：

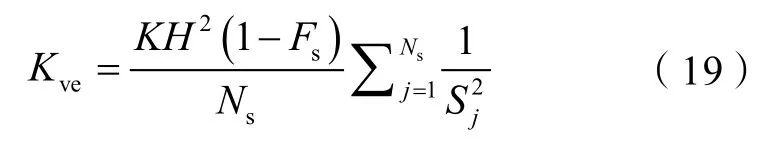
可见，一旦确定了每一根流管的迂曲度，那么垂向上受夹层影响后的等效渗透率均值就可通过（19）式计算。Green 等[4]基于统计理论给出了流动路径长度的计算公式：

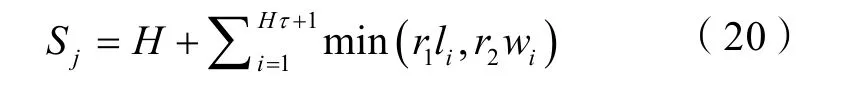
如果在储集层中存在足够多随机分布的泥质夹层，则每个流管遇到的泥质夹层个数是相对恒定的。在三维情况下，最短流动路径平均值为：

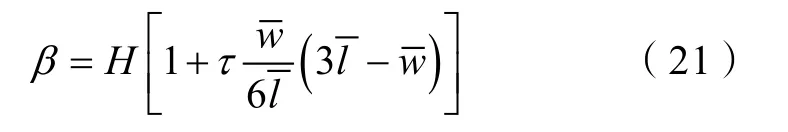
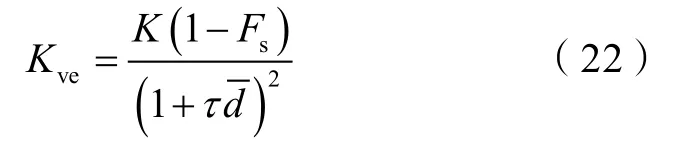
其中

由此可见，计算流动路径长度难题在于获得粗化网格内泥质夹层的平均长度和宽度。Deutsch 等[28]设计了一种在粗化网格中追踪砂岩体并计算连通砂岩体积的方法，其核心是将每一个粗化网格作为一个模型，其内部包含若干个细网格，选择其中一个细化网格，沿其相邻的网格找寻泥质夹层点（见图4）。在三维情况下，每个网格需要追踪相邻的26 个方向，获得该泥质夹层的连通范围。采用Deutsch 设计方法可获得泥质夹层三维体。本文将泥质夹层三维体分别投影到XOY、YOZ、ZOX 面，即可获得泥质夹层在Z 方向、X 方向和Y 方向的投影面积。在XOY 面上，沿X 或者Y 方向逐网格获得泥质夹层延伸长度或宽度，平均后即可获得泥质夹层在Z 方向上的平均长度和宽度，实现基于迂曲路径计算的泥质夹层的等效粗化。

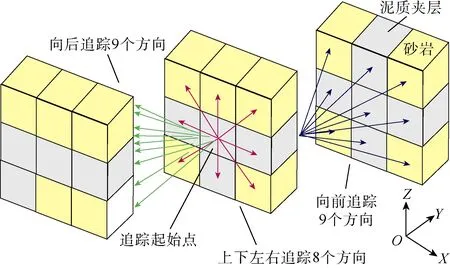
图4 网格追踪方向示意图

3.2 模型粗化

精细地质模型网格数量巨大，难以直接应用于油藏数值模拟，一般需要进行粗化处理，将千万级别网格节点数量等效为百万或十万级网格模型。由于夹层厚度薄，传统的粗化方法往往将其过滤掉，难以体现其对蒸汽腔发育以及油藏开发效果的影响，因此需要寻找新的粗化方法，最大限度保留泥质夹层的特征，满足精细数值模拟需求。

分别采用本文提出的迂曲路径计算、商业软件中通常采用的流动特征等效粗化方法对建立的精细模型进行粗化，粗化后网格数量为113×75×25=211 875 个。从粗化后的模型看，迂曲路径计算等效粗化模型（见图5）中由于夹层完全穿越整个粗化网格，因此存在渗透率为0 值的区域，可以体现泥质夹层对流体的遮挡作用；应用商业软件形成的流动特征等效粗化模型（见图6）很难发现夹层遮挡，渗透率值不存在0 值区域，仅在局部表现出显著降低。

图5 迂曲路径计算等效粗化模型

图6 流动特征等效粗化模型

进一步对比过井剖面（见图7）发现，与精细网格模型相比，迂曲路径计算等效粗化模型泥质夹层数量减少，但是泥质夹层在局部明显的遮挡作用得到保留；流动特征等效粗化模型仅显著降低了渗透率，并未对流体流动形成阻碍，未体现夹层的遮挡作用，可见迂曲路径计算等效粗化方法精度更高。

3.3 粗化结果验证

在粗化网格中选取一个局部区域（模型网格为50×50×25）对粗化方法的效果进行对比验证。分别以原始精细地质模型、迂曲路径计算等效粗化模型、流动特征等效粗化模型为基础进行SAGD 油藏数值模拟。

从模拟的温度场形态分布情况看（见图8），迂曲路径计算等效粗化模型与原始精细地质模型的结果较为相似，均表现为局部受夹层渗透率低（或为0）的影响，蒸汽难以波及，温度较低，蒸汽腔扩展受限，同时温度场分布不均匀；流动特征等效粗化模型蒸汽大范围波及，温度场分布较为均匀，蒸汽腔扩展未受阻，主要是因为流动特征等效粗化过程中过滤掉了夹层的遮挡作用，粗化后渗透率场相对平滑。

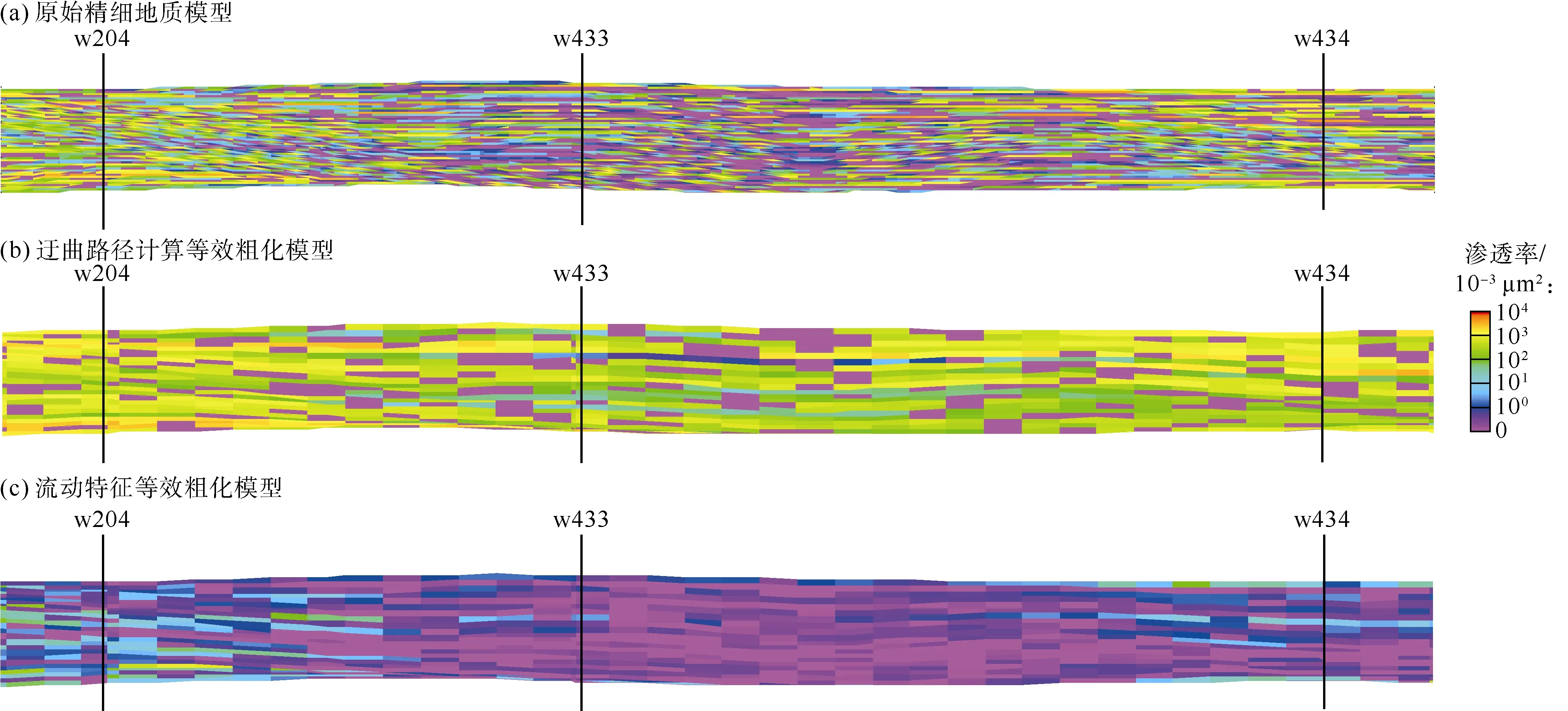
图7 过井剖面粗化结果对比

图8 3 种模型的模拟温度场分布对比

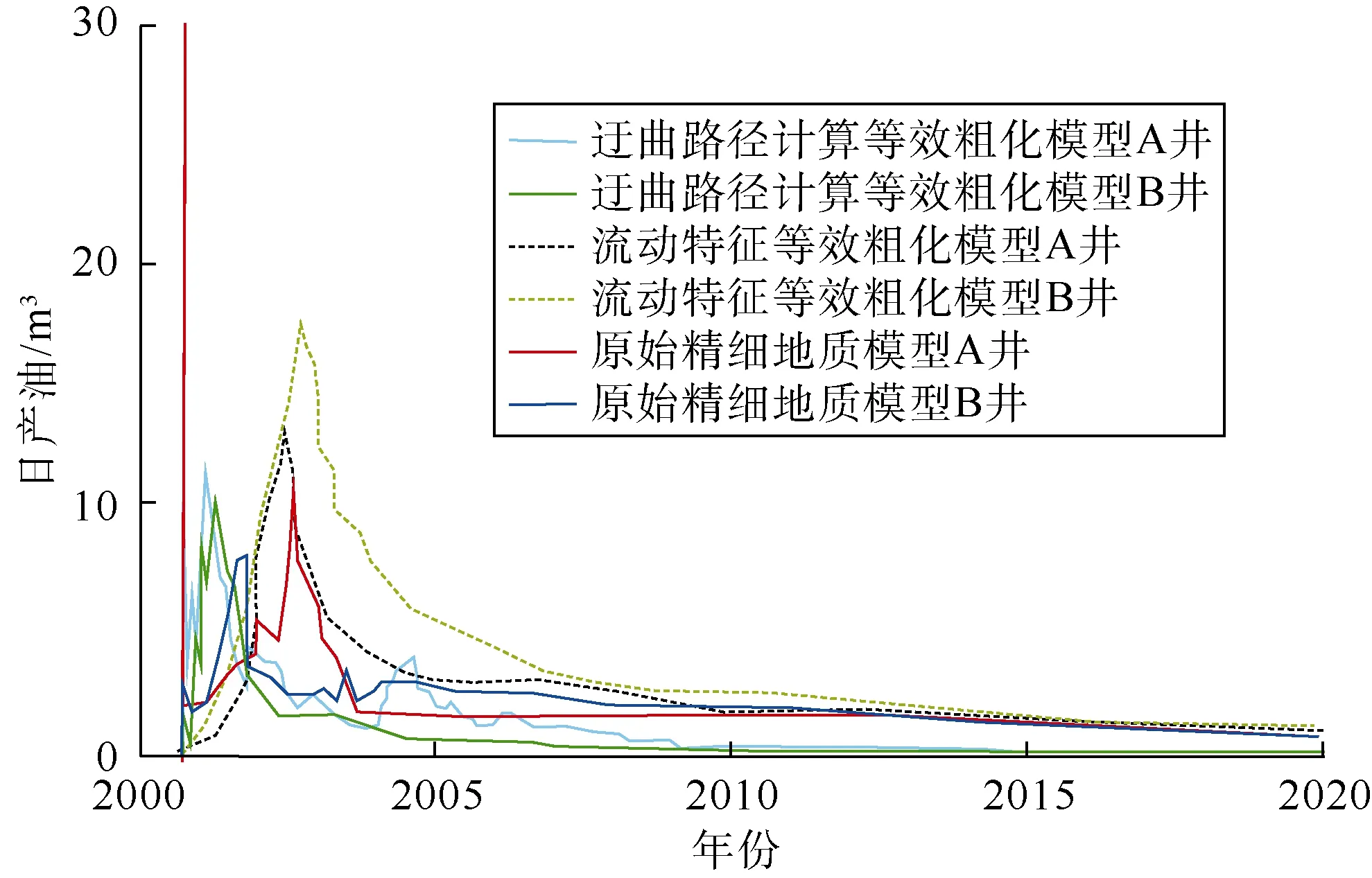
图9 3 种模型日产油量对比

从3 种模型的单井日产油开发指标对比（见图9，局部模型模拟结果）可以看出，流动特征粗化模型没有考虑夹层对渗流的遮挡效应，A 与B 井日产油量最高，初期与原始精细地质模型接近，中后期远高于精细地质模型；迂曲路径计算等效粗化模型两口井日产油量初始阶段与原始精细地质模型较为接近，产油峰值也接近，中后期则低于原始精细地质模型，这主要是因为模型粗化过程中泥质夹层全穿越网格时，将其渗透率设置为0，成为空网格，但泥质夹层很薄，仅占据粗化网格极小部分，粗化网格内还存在部分原油且可经侧向运移产出，网格粗化后该部分原油未参与计算，因此模拟计算中后期日产油量降低。

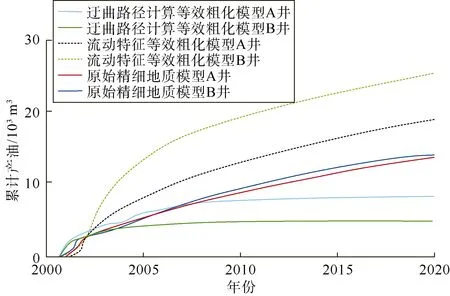
图10 3 种模型累计产油量对比

累计产油量指标对比（见图10，局部模型模拟结果）也有相似的规律，流动特征粗化模型两口井累计产油量较高，原始精细地质模型累计产油量居中，迂曲路径计算等效粗化模型最低。整体上看，迂曲路径计算等效网格粗化方法考虑了夹层的遮挡影响，其数值模拟结果与精细网格模型更为接近，也更能代表实际地质条件的影响，该方法是有效的。

该粗化方法应用于加拿大长湖油田西区受潮汐影响的曲流河点坝侧积层的粗化，粗化模型较好地体现了侧积层对开发的影响，拟合效果好。表明本文提出的方法能够适用于不同类型和产状的泥质夹层等效粗化。