数形结合助推数学问题“五化”

陈湘芬

数形结合不仅是一种教学方法，还是一种重要的数学思想。在小学教学中巧妙运用数形结合思想，可以使抽象的数学概念形象化、计算算理直观化、模糊情境具象化、复杂问题表象化、几何图形简约化，从而激活学生思维，拓宽学习思路，提高解题能力，让学生感受数学学习之旅的无穷魅力。

一、用形表数，数学概念形象化

概念教学是数学教学的难点，因为小学生以形象思维为主，理解抽象的概念知识有一定难度。借助直观模型，用形表数，可以把抽象的概念形象化，从而帮助学生在直观中理解抽象的数学知识。

在公开教学《3的倍数的特征》时，用百数表学生找到了3的倍数的特征，我趁机追问：“为什么2、5的倍数的特征只要看个位上的数就可以了，而3的倍数的特征要看各个数位上的数字和呢？”学生一下子就蒙了，探究中我借助信息技术数形结合一步步演示分小棒过程，如24根小棒先拿出20根，3根3根分余2根，余下的2根与4根合起来刚好6根，6是3的倍数，所以24是3的倍数。而且24中个位与十位相加2+4=6，因此得出，一个数各个数位上的数字和是3的倍数，这个数就是3的倍数。学生、听课教师顿时豁然开朗。巧用数形抓住数学本质，学生不仅知其然，更知其所以然。

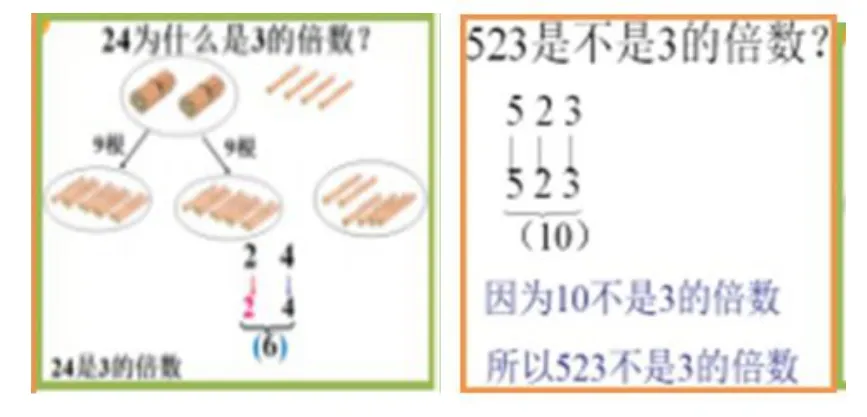
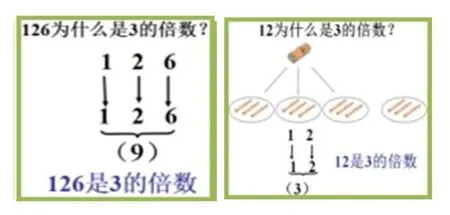
如《积的变化规律》一课，在学生初步感知积的变化规律后，我让学生将发现的规律应用于解决实际问题，感受由数的变化引起面积的变化。

计算长方形的面积：（单位cm）（见下左图）

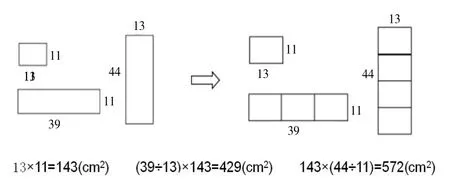
借助形的支撑，多数学生很自然地把左图变成了右图，通过对比，都能具体描述积的变化规律。

用形解数，最大程度地考量了小学生形象思维为主的现实，既可以由数解释形，也可以由形概括数，自然落实数形结合的思想。这样，学生不仅掌握了概念的特征，还深刻理解了概念的本质特征，有效地促使学生的知识结构实现了迁移。

二、化数为形，计算算理直观化

利用图形来直观地解释一些比较抽象的数学原理与事实，让人一目了然。尤其是对于小学生，其思维的抽象程度还不够高，可以借助直观模型来帮助理解。例如，利用面积模型来解释两位数乘两位数的算理，长方形模型来理解分数乘法的算理。

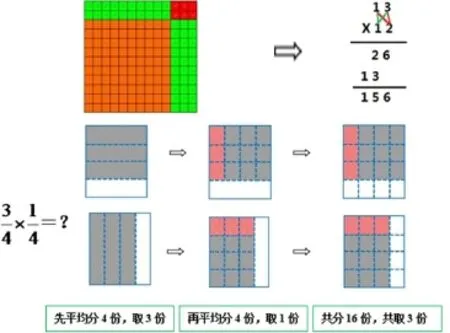
上面只展示两种折法(先横后竖）与（先竖后横）。学生通过动手折一折、涂一涂很快发现：在分数乘法中，遇到分数乘分数的问题，只要分子乘分子、分母乘分母就可以了（能约分的先约分再计算比较简便）。

一个简单的图形清楚地诠释了计算的道理，直观地演绎了数学计算过程，让学生对数学计算有更深入的认识和理解，原本抽象难懂的计算过程顿时生动形象起来，进而更好地提高学生对数学运算的应用意识。

三、借形想数，模糊情境具象化

数形结合思想，简单地说就是将数学中的语言及数量关系和直观几何图形相联系，进而达到举重若轻、轻松解题的目的。在许多数学问题中，已知条件看似容易，但学生要将问题的情境对应为数量关系有一定难度。这时，教师就可以运用数形结合思想，让学生借助图形更好地理清对应的数量关系，从而使模糊情境具象化，提高解题的正确率。

如用长13分米，宽5分米的长方形铁皮剪成几个半径为10厘米的圆做桶底，可以剪多少个圆？

学生一看到这题马上会想到用“大面积÷小面积”的方法，实际上这种解题方法是不适合的。因为实际生活中完整的圆剪下后余料是不可能再利用的。可以引导学生借助草图帮助理解。

如A、B、C、D、E五人进行乒乓球单循环赛，比赛进行一段时间统计如下：A已赛了4场，B已赛了3场，C已赛了2场，D已赛了1场，这时E已赛了几场？到比赛结束还需要进行几场比赛？

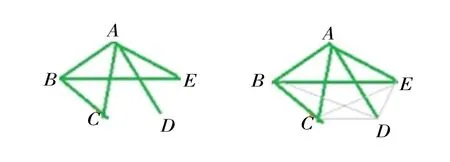
通过画图，结果一目了然：E已赛了2场。到比赛结束还需要进行4场比赛。就这样，巧用数形结合，让模糊数学问题清晰化，使学生在看得见、摸得着的情况下正确分析数量关系，寻找解决问题的策略，把学生的思维引向更深处。

四、以形解数，复杂问题表象化

利用数形结合平台，可以将抽象的数学知识转化成为便于学生理解的表象，降低学生的解题难度，同时培养学生的观察能力、推理能力、发散思维能力。

通过观察题目，大家都知道此题从简单开始一步步算。其实像算式可以引导学生画图理解（如下图）。学生发现只要用大正方形面积减去剩余面积即可，而剩余部分面积刚好是整个正方形的。即

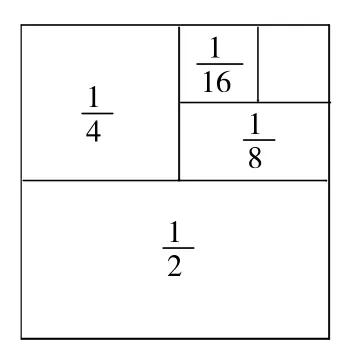
学生在计算过程中还发现加数有规律，后一个加数是前一个加数的。这些加数无限加下去，最后所得的和都等于1减去最后一个加数；加数的项数越多，和越接近1。但是这个无限接近于1的数到底是多少呢？利用面积模型，在模型上表示出这些加数，学生借助图形理解：无限加下去，最终的得数是1，感受极限思想。

又如，牧场上长满了牧草，而且每天都在匀速生长。这片牧场的草可供24头牛吃6天，或者供21头牛吃8天。那么，这片牧场上的草可供16头牛吃多少天？（假设每头牛每天吃草量相同）

这种题目可以先画图，再利用数形之间的关系来解答，降低解答难度。

1.先求每天长草量。

先把每头牛每天吃草量具体化，设1头牛1天吃1份草，那么24头牛6天吃草量24×6=144（份），21头牛8天吃草量21×8=168（份）。（见下图）

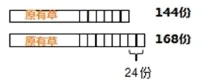
（168-144）÷（8-6）=12(份）。

2.再求原有草量。

144-12×6=72（份）。

3.最后求吃的天数。

72÷（16-12）=18（天）。

引导学生：每天新长草量12份，不够16头牛吃，只能派4头牛去吃原有的草量，所以原有草量每天减少4份。

数形结合，可以让抽象的复杂的“牛吃草”问题迎刃而解。学生在解疑的过程中，知识建构得既生动又深刻，同时还在解题中体会到了数学之美，感受到了数学学习的独特魅力。

五、用数示形，几何图形简约化

《九章算术》指出：析理以辞，解体用图。运用数形结合思想，将三视图与数字巧妙结合，使学生解决问题的方法更具有简约化与创造性，有助于培养学生的空间观念。

如求出下图的体积。（小正方体棱长为1cm）

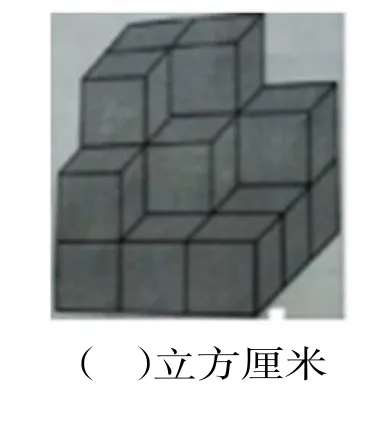
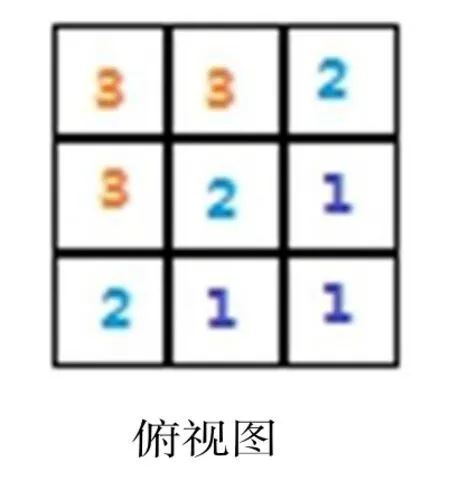
从平时的练习中发现，学生用数数的方法数错的也不少。但是利用俯视图（右上图），并在相应的位置注上数字，结果显而易见3×3+2×3+1×3=18（cm3），简单又正确。

这类还原立体图形题，可以数形巧结合，根据左视图和主视图推断出主视图相应格子中小正方体的个数，不用摆小正方体也能正确快速解答。

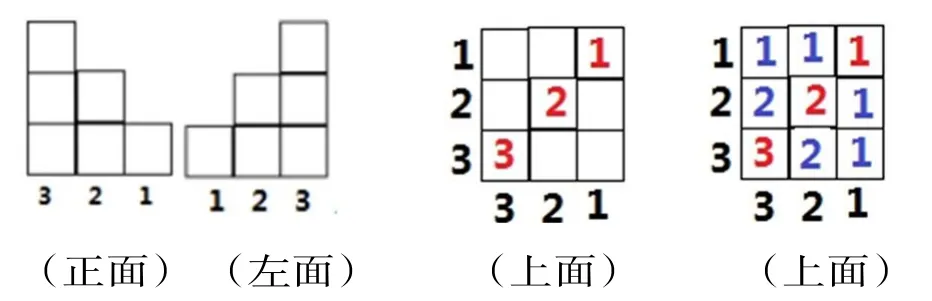
最少:3+2+1=6（个）最多:3+6+5=14（个）

实物图验证（见上图）。

著名数学家华罗庚教授曾经说过：“数缺形时少直观，形缺数时难入微。数形结合万般好，隔离分家万事非。”期待数学教坛同仁多多用心于数形结合，在实际教学中努力钻研教材，灵活运用数形结合思想，让数形结合思想渗透在数学教学的每个领域，真正走进学生的心灵，帮助学生更深刻地理解数学知识，体会数学之美，从而使数学学习成为怦然心动的魅力之旅。