基于地震灾害智能决策系统的中心选址
2017-03-31武警警官学院管理科学与工程系四川成都610213
周 帆(武警警官学院管理科学与工程系,四川成都610213)
基于地震灾害智能决策系统的中心选址
周 帆
(武警警官学院管理科学与工程系,四川成都610213)
针对应急救援中心选址提高救援效率的问题,依据地震灾害智能决策系统对受灾程度进行判断,综合考虑地震受灾点的严重程度与道路情况,以救援时间最小化为目标,建立应急救援中心选址优化模型,并运用Dijkstra算法进行求解.通过算例研究,获得应急救援的最优选址方案,表明理论具有可行性,为中心选址提供了理论参考.
中心选址;Dijkstra算法;地震灾害;智能决策
0 引言
近年来,我国地震灾害频发,像5.12汶川地震与4.14玉树地震等,都具有突发性与破坏性,地震的发生让人民的生命财产受到严重破坏与损失.在救援过程中,应急中心库可以对人员、药品、食品等调拨运输,建立合适的应急中心库,能够有效地减少救援时间,提高救援效率,有着不可替代的作用.因此,确定应急中心库的位置,是灾后应急救援的一个重要课题.
在选址的研究中,应考虑不同受灾程度,严重地点需要物资和救援力量更多且更为急迫,在救援过程中,会对受灾点多次进行运输.近年,武警部队开发了地震灾害智能决策系统,能够提供震后受灾点的严重程度与本地的交通地理情况,为应急中心的选址提供了依据.选址过程中,考虑道路情况与受灾程度综合选址,以减少救援的总时间,为救援提供参考.
1 基于地震灾害智能决策系统的选址模型分析
1.1 受灾程度分类
地震后,在地震灾害智能决策系统中输入震级、震源深度、建筑物情况、人口密度、地震发生时间等数据,系统就能在10分钟内推算出死亡、重伤、脑外伤、骨折等各类数据,为救援方案的制定提供参考.同时,系统可以查询展示受灾点的相应信息,如公共卫生资源、相关经济和社会信息叠加、地震特点信息等;还可以提供实时空间定位,分析地震灾害模型并生成最佳救援路径,综合受灾地点的各类数据,快速评估灾区伤害伤情.
地震灾害智能决策系统对地震区域的所有地点进行受灾程度的判断,根据伤亡人数、地区的防灾水平、所需物资、破坏程度等对各受灾点的受灾程度划分成5个等级,分别为特别严重,严重,中等,一般,轻微,根据受灾程度做出运输次数表:

表1 受灾程度与运输次数
1.2 道路分类
在地震之后,灾区的工作将以救援工作为重心,第一标准就是救援的时间,如果能缩短救援路途中所花费的时间,就能使救援行动更加有效.因此,在救援的实际行动中,救援车辆将会在道路允许的情况下,行驶至最大速度.所以,依据《中国人民共和国道路交通安全法》中的第四十二条、第六十七条,《中国人民共和国道路交通安全法实施条例》的第四十五条、第七十八条,关于机动车辆在道路行驶时的限速问题,对所有道路类型及速度进行划分如下:

表2 道路类型与速度
因此,假设,救援车辆在各类道路上的行驶速度为上表所示速度.
1.3 构建模型
建立一个救援中心,设有m个受灾点,n个道路节点,其中受灾点也可作节点.利用地震灾害智能决策系统,各个节点为各级道路之间的交接点,对受灾地区的所有道路情况进行归类汇总,得出各节点和受灾点之间的一步可达距离矩阵为:
单位为km,其中矩阵中的自身可达,可达距离表示为0, 两节点如果不可达,则在相应节点表示距离为无穷大,然后根据在各类路段的行驶速度,建立各个节点之间路段的速度矩阵为:
单位为km/h.用距离矩阵与速度矩阵进行点除运算得出各节点到达各节点的时间矩阵为:
L=S./V
计算得:
表示为各个节点之间路段所需的时间矩阵,其中单位为小时.然后根据受灾程度与受灾点一一对应,建立运输次数矩阵:
E={e1…em}T
(4)
运用Dijkstra算法计算出各个节点到所有受灾点的时间,并建立各节点到各个受灾点的时间向量:

(5)
各节点到所有受灾点总时间矩阵
Ti=E·ti
(6)
取最小值:
Min(T)=Ti(1im+n)
(7)
i所对应节点为选择节点,式中tij为从i节点到j受灾点的时间,Ti为节点i到所有受灾点时间之和, 选出最佳节点之后,利用二分法,选择此节点到下一步可达节点的中点,并对L中相应时间信息进行更新,令
K=L
(8)
K(i,j)=K(i,j)-1/2K(i,j)
(9)
K(i,k)=K(i,k)+1/2K(i,j)
(10)
j为i节点移动方向上的相邻节点,k表示与i节点直接相接的其他节点.更新之后,计算总时间,取总时间最小值所对应的节点方向路段,对所选路段进行分段.因为时间单位为小时,为了减小误差,确保时间最优化,把变量控制在一分钟以内,u为路段划分的段数
u=K(i,j)/0.01
(11)
路段有u-1个节点,每一个节点为i节点的更新点,更新时间矩阵信息后,求各个更新点到所有受灾点的总时间,得矩阵:
A={a1…au-1}
(12)
求最小值:
MinA=ax
(13)
如果ax
2 算例分析
设置20个节点,其中7个受灾点,受灾程度分别为特别严重、严重、严重、中等、中等、一般、轻微,依据(6)可得:
E={100,70,70,40,40,20,5}T
因为只涉及一个中心库的选址,而现实情况下的中心库不会只有一个,所以所设的节点之间的距离,距离均不大于200km,且自身可达,生成距离矩阵为:

表3 可达距离矩阵S
各道路行驶速度矩阵为:

表4 速度矩阵V
运用MATLAB软件和Dijkstra算法计算:
L=S./V
得时间矩阵t为:

表5 时间矩阵t
计算时间矩阵T:
Ti=E·ti
得:
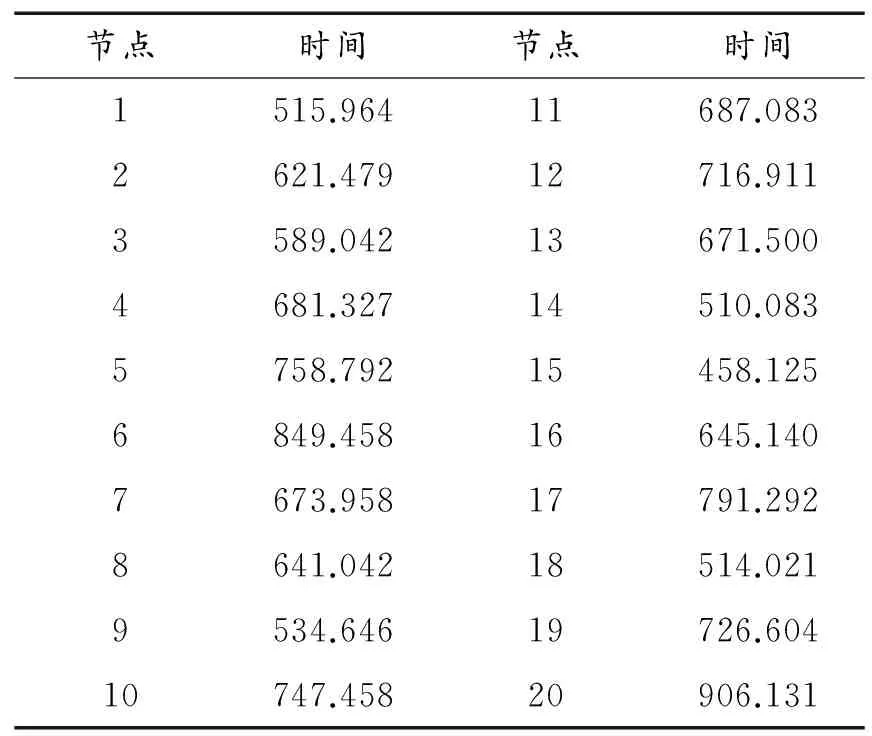
表6 时间矩阵T
Min(T)=T15
Min(Tik)=T15(1)
u=87.5≈87
ax=459.1>T15=458.0
综上所述,此次中心选址的最佳点为节点15,其坐标可通过图上信息求得.
3 结束语
本文主要运用Dijkstra算法,对不同受灾程度,以及现实道路情况下的中心选址进行了研究,为灾后救援的中心选址提供理论参考.本文在地震灾害智能决策系统的基础上,对受灾点的运输次数进行分类,并依据灾区现实道路情况进行建模,求解运输时间最少的最佳中心库地址.在实际的选址过程中,要结合实际情况选择,可能最优点并不适合建立中心库,此时需要寻求次优点.本文旨在通过数据分析的方式,选择出最好的中心库地址,以提高救援的效率,为灾后的救援行动奠定基础.
[1] 董文龙,丁 辉,樊毫军,侯世科.地震灾害救援智能决策系统平台的研制[J]. 中国急救复苏与灾害医学杂志,2014(9):796-799.
[2] 韦 晓,常相全.基于改进蚁群算法的应急物流中心选址问题研究[J]. 价值工程,2014(17):26-27.
[3] 骆达荣.基于灾度相对分类的应急物流中心选址[J]. 技术经济与管理研究,2013(7):105-109.
[4] 曹振华,王宇翔.基于Dijkstra算法的区域物流网络配送路径优化[J]. 物流技术,2015(2):146-147.
[5] Feng Ye,Qiuhong Zhao,Menghao Xi.ChineseNationEmergencyWarehouseLocationResearchbasedonVNSAlgorithm[J].Electronic Notes in Discrete Mathematics,2015(87): 425-435.
[6] ReVelle C.S.,Laporte Gilbert.ThePlantLocationProblem:NewModelsandResearchProspects[J].Operational Research,1996(6):864-874.
[责任编辑 范 藻]
The Central Location of the Intelligent Decision System Based on Earthquake Disaster
ZHOU Fan
(Management and Engineering Department of Officers College of PAP, Chengdu Sichuan 610213, China)
In order to improve the efficiency of emergency rescue center location problem, based on the intelligent decision-making system for earthquake disaster to determine the extent of disaster, and the severity of the road considering the earthquake disaster point, the rescue time is minimize as the goal, establish emergency rescue center location optimization model, and using Dijkstra algorithm. Through a case study, the optimal location scheme of emergency rescue is obtained, which shows that the theory is feasible, and provides a theoretical reference for the center location.
Center location; Dijkstra algorithm; Earthquake disaster; Intelligent decision
2016-12-24
周 帆(1995—),男,湖南岳阳人.主要从事应急救援研究.
F259.21
A
1674-5248(2017)02-0018-04
