基于上凸序列的修正GM(1,1)模型

孔新海，马 新，梁少林(.广安职业技术学院，四川广安68000；.西南科技大学理学院，四川绵阳600；.四川文理学院财经管理学院，四川达州65000)

基于上凸序列的修正GM(1,1)模型

孔新海1，马 新2，梁少林3
(1.广安职业技术学院，四川广安638000；2.西南科技大学理学院，四川绵阳621010；3.四川文理学院财经管理学院，四川达州635000)

针对GM(1,1)模型对上凸序列建模时会出现误差较大的情况进行了研究.证明了GM(1,1)模型的还原序列为下凸序列，分析了其对上凸序列建模时的残差变化规律，并提出了通过对称变换把上凸序列转化为下凸序列再建GM(1,1)模型的一种新方法.实例也证实了新方法比原始GM(1,1)模型具有更高拟合精度.

上凸序列；GM(1,1)模型；对称变换

灰色预测模型是灰色理论中重要的组成部分，是处理小样本和贫信息的重要工具.GM(1,1)是灰色预测模型中最重要并且应用最广泛的模型.近年来，GM(1,1)模型已被广泛地应用于工业生产、社会科学等各个领域.[1-2]但是在实际的应用过程中，GM(1,1)模型也会出现误差较大的情况，因此许多学者提出了一系列的改进方法.文献通过对白化方程的分析，[3-5]得出了背景值的准确计算公式；文献使用非齐次指数函数来拟合其累加生成序列，[6]重新推导了新的背景值计算公式，突破了发展系数的限制.文献分别采用加权最小二乘和总体最小二乘法对GM(1,1)参数估计方法进行了改进.[7,8]文献则分别通过优化白化方程的初值和边值对GM(1,1)模型进行了改进.[9,10]然而，无论采用上述哪一种方法，用GM(1,1)模型对原始序列进行模拟预测时，其还原值序列总为下凸序列.如果对于上凸序列进行建模，则会导致预测序列与原始序列发展趋势不一致.为了克服这种模型误差，文中提出用对称变换把上凸序列先转化为下凸序列再建GM(1,1)模型的方法.

1 序列凸性的定义

定义1 对于某一序列x(0)={x(0)(1),x(0)(2),…,x(0)(n)}，若满足Δ(0)(k)Δ(0)(k-1) (2kn)时，则称序列x(0)为上凸序列；若满足Δ(0)(k)≥Δ(0)(k-1)(2kn)，则序列x(0)为下凸序列，其中Δ(0)(k)=x(0)(k)-x(0)(k-1).特别地，当Δ(0)(k)<Δ(0)(k-1)(或Δ(0)(k)>Δ(0)(k-1))时，称序列x(0)为严格上凸(或下凸)序列.

定理1 若序列x(0)={x(0)(1),x(0)(2),…,x(0)(n)}是上凸(或下凸)序列，则满足不等式：

2x(0)(k)≥x(0)(k+1)+x(0)(k-1)

(1)

或

2x(0)(k)x(0)(k+1)+x(0)(k-1))

(2)

证明：设x(0)={x(0)(1),x(0)(2),…,x(0)(n)}是上凸序列，则由定义1可知：

2x(0)(k)=(x(0)(k+1)-Δ(0)(k+1))+(x(0)(k-1)+Δ(0)(k)) =(x(0)(k+1)+x(0)(k-1))-(Δ(0)(k+1)-Δ(0)(k)) ≥x(0)(k+1)+x(0)(k-1)

(3)

特别地，当x(0)为严格上凸序列时，上式不含等号.同理，可证x(0)为下凸序列时，(3)式不等号反向.

2 灰色GM(1,1)模型及其特性

x(0)(k)+az(1)(k)=b

(4)

为GM(1,1)模型的基本形式；连续微分方程

dx(1)/dt+ax(1)=b

(5)

称为GM(1,1)模型的白化方程.(4)式的最小二乘估计参数满足关系

[a,b]T=(BTB)-1BTY

式中

B=-z(1)(2) 1

-z(1)(3) 1

⋮ ⋮

-z(1)(n) 1,Y=x(0)(2)

x(0)(3)

⋮

x(0)(n)

把参数a,b的估计值代入(5)式,求解白化方程然后离散化,可得相应的时间响应序列为

(0)(k+1)=(1-ea)(x(0)(1)-ba)e-ak

(6)

在利用GM(1,1)模型进行建模时，通常都是正数序列，而在这种情况下GM(1,1)模型的模拟和预测序列也通常都是正数(极少数数据异常的情况除外).因此本文仅对GM(1,1)模型的输出序列为正数的情况进行讨论.以下定理给出了GM(1,1)模型在上述情况下的凸性.

定理2 当GM(1, 1)模型的输出序列均为正数时，则其输出序列为下凸序列.

证明：由于GM(1, 1)模型的输出序列均为正数，亦即(6)式的值在对一切k=1,2,…都是正数，此时有

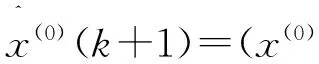
(7)

为方便叙述，记C=(x(0)(1)-b/a)(1-ea).注意到e-ak>0，因此C>0.考察增量序列

和

将(8)式与(9)式相比，有

(i)当a>0时，有e-a<1，因此(10)式小于1，即

Δ(0)(k+1)Δ(0)(k)<1

(11)

Δ(0)(k+1)>Δ(0)(k)

(12)

(ii)当a<0时，有e-a>1，因此(10)式大于1，即

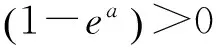
Δ(0)(k+1)>Δ(0)(k)

(14)

综上，根据定义1知GM(1, 1)模型的还原式(6)在定理的条件下得出的序列为下凸序列.

注意到上述定理中未讨论a=0的情况.虽然在实际的计算中可能会出现这种情况，但在这种情况下GM(1,1)无意义，因此定理2满足大多数实际计算的情况.

定理2 证明了GM(1,1)模型的还原值实际上是一个下凸序列，因此用GM(1,1)模型对上凸序列直接建模会产生很大的误差.如图1所示，当原始序列是上凸序列时，用(6)拟合计算得到的序列与原始序列的几何形状不一致.

3 凸序列的对称变换

由上面的分析可知，只要把上凸序列转换成下凸序列就可以避免这种模型误差.凸性转换最有效的方法就是轴对称变换.对于单调递增的上凸序列，可以按y=x(0)(n)进行对称变换；对于单调递减的上凸序列，可以按y=x(0)(1)进行对称变换；对于具有极值点的上凸序列，可以极值点为分界点，把原序列分成单调递增上凸序列和单调递减上凸序列.

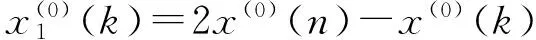
证明：若X(0)为单调递增上凸序列，则

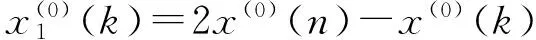
对于X(0)为单调递减上凸序列，同理可证.

4 基于上凸序列的修正GM(1,1)模型

对于上凸序列建立GM(1,1)模型，先要对原始序列进行对称变换，然后对变换序列建立GM(1,1)模型，最后再逆变换还原.下面给出具体的算法流程.

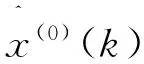
5 实例分析

例1[11]2003～2008年我国人均能源消费量为X(0)={1427,1647,1810,1973,2128,2200}，单位：千克标准煤.这是个单调递增的上凸序列，如果分别用原始GM(1,1)和数据经对称变换之后的GM(1,1)建模，模拟结果如表1所示.

表1 单调递增的上凸序列模拟结果

从表1可以看出，原始单调递增的上凸序列经对称变换之后建立的GM(1,1)模型，其拟合的平均相对误差要明显小于直接用GM(1,1)建模的平均相对误差.

例2[12]某油田在递减阶段的年产量为：X(0)={14.38,14,13.06,12.09,10.98,9.88,8.27}，单位：107t/a.这是个单调递减的上凸序列，如果分别用原始GM(1,1)和数据经对称变换之后的GM(1,1)建模，模拟结果如表2所示.

表2 单调递减的上凸序列模拟结果

表2结果同样显示：对于单调递减上凸序列，经对称变换之后建立GM(1,1)模型，其拟合效果要好于直接建立GM(1,1)模型.

6 结论

由前面的证明可以知道，GM(1,1)模型还原序列具有下凸性，对于下凸序列，如果直接用GM(1,1)建模，会导致预测序列的趋势与原序列的发展趋势不一致.经过进一步分析发现，采用GM(1,1)模型对上凸序列进行拟合时，单纯从GM(1,1)模型本身入手进行改进，并不能明显地提高GM(1,1)模型的精度，甚至还可能出现误差变大的情况.通过引入对称变换，把上凸序列转化为下凸序列，从根本上解决了模型误差.而对称变换函数的选择具有多样性，将在另文中讨论.

[1] Ma X, Luo D, Ding X F, et al.AnalgorithmbasedontheGM(1, 1)modelonincreasingoilproductionofmeasuresoperationforasinglewell[C]//2013 IEEE International Conference on Grey Systems and Intelligent Services, 2013: 158-160.

[2] 王宇熹, 汪 泓, 肖 峻. 基于灰色 GM(1,1)模型的上海城镇养老保险人口分布预测[J]. 系统工程理论与实践, 2010(12): 2244-2253.

[3] 谭冠军.GM(1.1)模型的背景值构造方法和应用[J]. 系统工程理论与实践, 2000(4): 98-103.

[4] 罗 党,刘思峰,党耀国.灰色模型GM(1, 1)优化[J]. 中国工程科学, 2003(8): 50-53.

[5] 刘 乐, 王洪国, 王宝伟.基于背景值构造方法的 GM(1,1)模型优化[J]. 统计与决策, 2009 (1): 153-155.

[6] 王正新, 党耀国, 刘思峰. 基于离散指数函数优化的GM (1,1)模型[J]. 系统工程理论与实践, 2008(2): 61-67.

[7] 何 霞. 灰色 GM(1,1) 模型参数估计的加权最小二乘方法[J]. 运筹与管理, 2012(6): 23-27.

[8] 袁 豹, 岳东杰, 李成仁. 基于总体最小二乘的改进 GM(1,1)模型及其在建筑物沉降预测中的应用[J]. 测绘工程, 2013(3): 52-55.

[9] Wang Y, Dang Y, Li Y, et al.AnapproachtoincreasepredictionprecisionofGM(1, 1)modelbasedonoptimizationoftheinitialcondition[J]. Expert Systems with Applications, 2010(8): 5640-5644.

[10]张 彬, 西桂权. 基于背景值和边值修正的 GM (1, 1) 模型优化[J]. 系统工程理论与实践, 2013(3): 682-688.

[11]中华人民共和国国家统计局编. 中国统计年鉴[M].北京：中国统计出版社, 2009：24-27.

[12]孔新海,刘志斌,魏 勇. 单调递减序列的离散变换及其灰色建模[J]. 统计与决策, 2012(10): 19-21.

[责任编辑 范 藻]

On the Improved GM(1, 1) Model Based on Concave Sequence

KONG Xinhai1, MA Xin2, LIANG Shaolin3

(1.Guang'an Vocational and Technical College, Guang'an Sichuan 638000;2. Science School of Southwest University of Science and Technology, Mianyang Sichuan 621010;3.Finance-Economy Management of Sichuan University of Arts and Sciences, Dazhou Sichuan 635000, China)

The issues of big errors of GM(1, 1) model for concave sequence modeling have been studied in this paper. Firstly, the restored sequence of GM(1,1) model is proved to be concave, and the characters of residuals of GM(1, 1) model built on concave sequence have been analyzed. Secondly, two symmetry transformations are introduced to transform the original concave sequence, and then built the GM(1, 1) model based on the transformed sequence. The new method has been compared to the traditional modeling method, and the results show that the accuracy of the new method is very high, and it is applicable for all concave sequence modeling.

Concave sequence; GM(1, 1) model; Symmetry transformation

2016-11-10

四川省教育厅一般项目“难采储量评价方法及其应用研究”(14ZB0388)

孔新海(1983—)，男，江西余干人.讲师，博士，主要从事灰色系统理论方法研究.

N941.5

A

1674-5248(2017)02-0007-04