浅析初中数学几何推理与图形证明方法

秦汉文

【摘 要】初中教学中，数学课程是重点组成成分之一。数学知识具有抽象性、理论性和逻辑性较强的特点，学生在学习的过程中难度较大，几何推理与图形证明是初中数学知识的重点内容之一，是初中生数学知识学习过程中的一大难点。正因为如此，教师在实际教学过程中，必须从提升学生的图形想象能力和空间思维能力入手，才能够帮助学生加深对知识的理解，并提升正确解题的能力。在这种情况下，本文从初中数学几何推理与图形证明教学中的缺陷入手，从抓住题干要素正确解题的方法、几何推理与图形证明教学中引入定理和重要概念等方面入手，对提升初中数学几何推理与图形证明教学质量的方法展开了探讨。

【关键词】初中数学 几何推理 图形证明 方法

【中图分类号】G633.63 【文献标识码】A 【文章编号】2095-3089（2016）34-0233-01

一、初中数学几何推理与图形证明教学中的缺陷

现阶段，我国的初中数学教学过程中，几何推理与图形证明是难点和重点内容之一。学生在对这部分知识进行学习的过程中，需要具备较强的抽象性思维和空间想象力。然而，现阶段我国部分初中数学教师在教学过程中，仍然沿用传统的教学模式，即在详细讲解课程重点理论知识的基础上，通过大量的习题，引导学生内化知识内容。这种教学模式在应用过程中，教师是课堂主体，学生作为客体，只能够对理论知识进行死记硬背，然而较强的理论性和逻辑性知识，不仅导致学生在记忆过程中难度较大，同时学习兴趣大大下降，在长时间的知识学习过程中，很容易产生对各种理论的混淆，学生的几何推理思维和图形证明能力无法得到有效培养。由此可见，传统以教师为主的教学模式不利于提升初中数学教学质量，新时期，教师必须从以下两方面入手，切实提升学生的解题能力，才能够为培养学生的數学素养奠定良好的基础。

二、抓住题干要素正确解题

初中数学几何推理与图形证明教学中，教师应将各种类型的例题引入课堂，帮助学生对知识点进行消化和理解才能够提升教学效率和质量。在例题的讲解中，首要任务就是培养学生正确的“读题”能力。事实上，题干看起来短小，但是其中包含了大量的关键要素，是解题和证明的关键，在读题中，教师应引导学生拆解题干，将其中的重要要素提取出来，并挖掘隐含的条件，从而为构建清晰的解题思路奠定良好的基础。如果题设相对复杂，学生更应当具备抽丝剥茧的能力，将题设中的各个要素提取出来，在对各个要素进行排列的过程中，应结合图形进行，并将这些要素应用于证明问题的过程当中。读题的能力需要教师在教学过程中长期对学生进行引导，才能够促使学生在解题的过程中，不受其他因素的干扰，做出正确的判断，并提升解题速度。

三、几何推理与图形证明教学中引入定理和重要概念

在几何推理中，根本性因素是定理，在对定理进行推广的过程中，可以演变出更多的几何推理与图形证明知识。在这种情况下，教师在实际教学过程中，应积极引进各种定理和概念。同时，较高的概括性是定理的主要特点，如果一味的要求学生进行死记硬背，不仅不利于提升学习效率和质量，甚至还很容易打击学生的学习积极性，因此定理和相关概念的引入，必须注重应用科学的方法。在反复应用相关定理的基础上，多数几何推理题都能够迎刃而解。

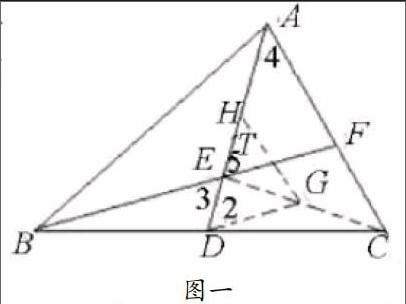
例如，在以下例题中，教师就可以适当的引入定理，帮助学生对理论知识进行掌握和深入理解的同时，提升学生实际解题的能力。“已知三角形ABC如图一所示，边BC的中点为D，连接AD，E为AD上任意一点，并连接、延长BE，F是AC与BE的交点，此时AC=BE，那么证明EF=AF。”单纯的解读题干可以发现，题目内容相对复杂，然而，在对题干进行深入挖掘的过程中学生就能够意识到，该题干描述的是等腰三角形，而所涉及的定理是“等边对等角”。在这种情况下，学生通过对“中点”、“三角形”等基础知识的联想，就会意识到需要对HG和DG等辅助线进行构建，接下来，在进行角与角之间的转换过程中，需要对平行线段性质以及等腰三角形相关性质进行应用，最后在完成证明的过程中，对“等角对等边”的理论进行应用。

在这种情况下，实际证明过程如下：连接EC，G为EC中点，H为AE中点，接下来，分别对HG和DG进行连接，那么可知DG=GH。因此角1和角2相等，由于角2、角3、角5是相等的，而角1同角4是相等的，那么则说明角4同角5相等，因此可以得到AF=EF。

由该例题可以看出，在实际的几何推理与图形证明教学中，要求学生能够对各种定理进行充分的了解，并提升学生灵活应用定理的能力，才能够顺利解答任何题型。

结束语：

综上所述，同小学数学知识相比，初中数学知识难度更大、理论性和逻辑性较强，其中一个关键的教学难点就是几何推理和图形证明，学生在实际解题的过程中，必须能够对各种原理和概念进行灵活的运用，而对题干进行正确的解读，并快速准确的找到重点要素是学习几何推理和图形证明知识的关键。教师在教学过程中，应注重数形结合教学模式的科学应用，引导学生在实际解题中对原理和概念进行更加深入的掌握，并通过灵活应用原理和概念，提升解题能力。