额外维个数及尺度对Casimir引力的影响

赖劼

（广东技术师范学院天河学院，广东广州 510540）

1948年荷兰物理学家亨德里克·卡西米尔提出了Casimir效应 （卡西米尔效应）[1],即两块靠得足够近的金属板将会产生相互吸引的现象，这个吸引力被称作Casimir力：

它由普朗克常数ħ，光速c，和平板间的距离a的关系式来表示，它是作用于真空中的两块平行理想导体板单位面积相互的力,随后的实验验证了该吸引力的存在。Casimir效应是一种有关真空涨落的量子现象，它起源于当量子化体积有边界或者所在的空间为非欧几里得时的真空扰动振幅的变化[2]。Casimir效应应用到物理学各个方面，包括弦论、基本粒子物理、M理论、宇宙学、拓扑缺陷、凝聚态物理的研究领域中都出现了有关Casimir效应的研究工作。

1 额外维对Casimir力的影响

为了探讨额外维的个数及尺度对Casimir力的影响，我们分别就 3+1维、3+2维、3+3维情况下的Casimir力进行分析：

应用Casimir能量的定义：

由Casimir力等于能量的负导数，则Casimir压强即为对能量求偏导数：

为了计算出Casimir压强，根据第三类贝瑟尔函数的第一种变换式[3]：

我们得到存在1个额外维Casimir压强：

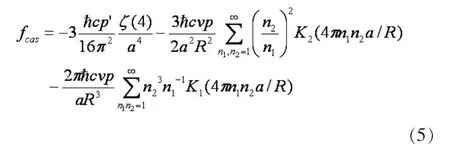
存在2个额外维Casimir压强：

存在3个额外维Casimir压强：

将不同额外维Casimir压强的计算结果式 （5），式（6），式（7）进行数值比较。 得到式（5）、式（6）、式（7）在测量平行理想导体板的实验误差范围在10%之内的考虑下，通过将存在额外维的平板计算的平板的力的结果进行优化处理，将得到了在实验的误差范围内对额外维尺度大小的限制。平板间距离与额外维尺度大小的比值μ，通过这个比值大小的变化，我们可以清楚的得到额外维个数的增多，对额外维尺度大小的影响。在误差范围内，额外维个数对额外维尺度大小限制的变化。当两个额外维的尺度不同时，在误差范围内，对额外维尺度大小限制的变化，结果表明当额外维的一个尺度在变小时，在实验的误差范围内，平板间距和另一个额外维的尺度的比值在变小，即对这一个额外维尺度的限制范围在变大。也就是说，要使额外维存在的条件满足，与板间距相比的这一个额外维的尺度大小可以控制在一个更大的范围内。并且，我们可以通过观察发现，当两个额外维的比值为0.2时，此时的板间距和其中一个额外维的比值等于只存在一个额外维，即5维时空的情况，也就是说，当两个额外维的比值为0.2时，就与只存在一个额外维的情况没区别了，而且，此后板间距同其中一个额外维的比值将不再发生变化，此时与板间距相比的那个额外维尺度的大小将对Casimir效应起到主导的作用。

我们将（5），式（6），式（7）数值计算结果制成表格1，以便对额外维尺度的增加，在误差范围内额外维尺度的限制的变化进行直观的分析（其中= μ）。

表1 额外维尺度的限制的变化

通过表1，我们可以得出结论：我们发现板间距同额外维的尺度的比值确实因为额外维的个数的增加而变大，即对额外维的尺度的限制范围变小。也就是说，要使额外维存在的条件满足，额外维的尺度大小需要控制在一个更小的范围内。这样我们就可以证明出额外维个数的增加反而限制了额外维尺度的大小。

为了对不同额外维个数下Casimir压强随板间距离a变化有一个直观的比较，我们将这三个结果进行绘图分析，为了方便绘图，我们令额外维的尺度大小都取 R，且 R=1，这样式（5），式（6），式（7）计算的数值作出了以下的图1。图1表示出了沿与平板面垂直方向的Casimir压强，分别在3维时空，3+1维时空，3+2维时空和3+3维时空尺度当R=1时的变化。

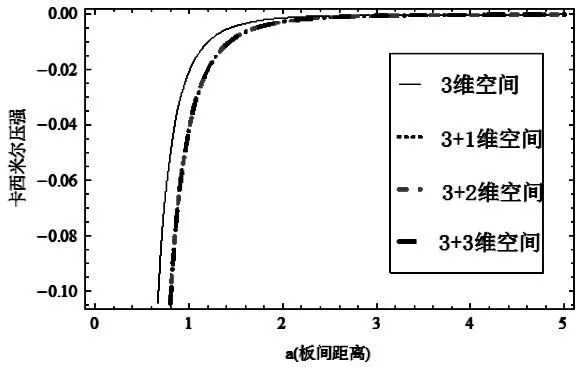
图1 不同维度Casimir压强变化趋势

我们令式（6）中的 R1=R2=R，式(7)中的 R1=R2=R3=R，这样式（5），式（6），式（7)的结果就会出现三项相同的项，而这三项刚好是式（5）的结果。为了清楚的得到额外维个数以及尺度大小的影响，我们需要从式（5），式（6）和式（7）中将这三项单独分析，在跟式(6),式（7）剩余各项的结果分别进行数值比较，可得出以下结论：

为便于分析，我们令公式中，则相同的三项为：

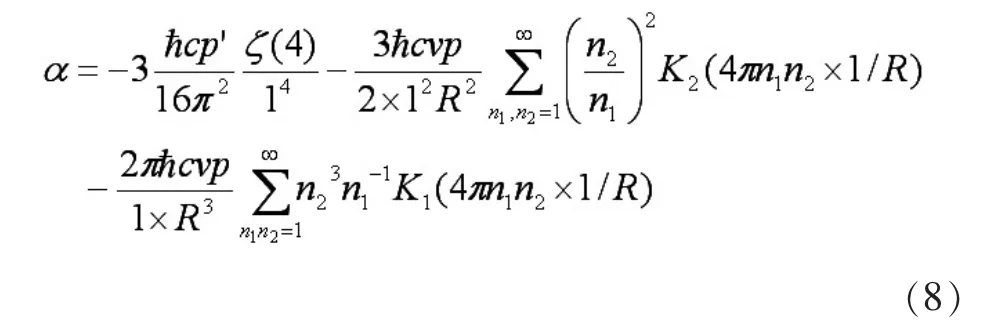
我们看到这里的α其实就是式（5）中的a=1的结果。

对于式（6），我们摘除上面的那三项后，同样取a=1，剩余的各项为：

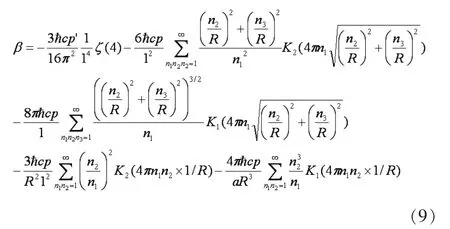
同理，对于式（7），我们摘除相同的三项后，取α=1，剩余的各项为：

对α，β，γ这三个参数式分别进行数值分析时我们取 ħ=c=1，以及 p′=2，p=3。

表 2 是在分别取 R=1，2，3，4，5 的值时，α，β，γ 三式的具体对应数值。

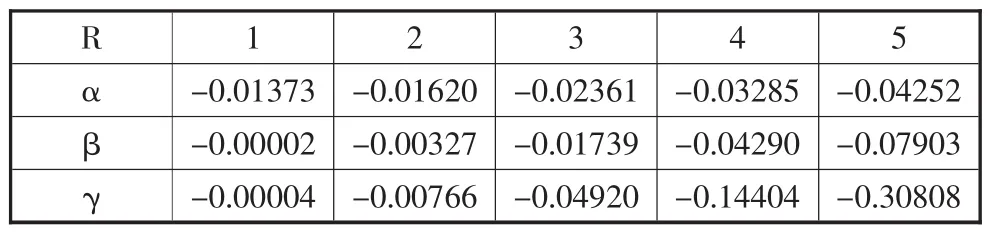
表2 α，β，γ变化数值

从表2中，我们可以得出结论：当额外维尺度时R=1，式（6），式（7）中起主导的项是跟式（5）中相同的那三项α，而当额外维尺度R≥2后式（6）和式（7）中除此三项以外的其余各项β，γ也开始发挥作用，我们看到而当 R=3时式（6）和式（7）剩余的项 β，γ的数量级已经跟式（5）中的那三项α的数量级相当了，当R≥4之后，剩余项β，γ的数值甚至超过了式（5）中那三项α的数值。

2 结语

通过表2的纵向比较也表明了随着额外维个数的增加，Casimir吸引力是越来越来大的。并且额外维的尺度的大小对Casimir力也有影响，当额外维尺度R≥1时，额外维的个数几乎对Casimir力的大小无影响，当R≥2时，额外维的个数才开始对力的大小发挥作用。

[1]Casimir HBG.On the attraction between two perfectly conducting plates[J].Proc K Ned Akad Wet，1948（51）:793-795.

[2]J.Strathdee.Kaluza-Klein Theory[J].Mod.Phys.A，1986（1）:1.

[3]王竹溪，郭敦仁.特殊函数概论[M].北京：北京大学出版社，2000.