不同晶体模型的微波布拉格衍射

郑 航，吴奕初，杨 薇，刘海林,李美亚

(武汉大学 物理科学与技术学院，湖北 武汉 430072)

不同晶体模型的微波布拉格衍射

郑 航，吴奕初，杨 薇，刘海林,李美亚

(武汉大学 物理科学与技术学院，湖北 武汉 430072)

研究了不同晶体模型下布拉格衍射规律，讨论了简单立方(100)晶面微波衍射图出现2级衍射和3级衍射所需的条件. 将简单立方模型改造成四方模型，讨论了四方晶体模型的衍射峰随晶面间距的变化规律. 设计了体心和底心立方模型，并观察到了(100)晶面的消光现象. 采用有限点阵理论模拟计算结果也与实验测量数据一致.

微波;布拉格衍射;晶体模型;晶面间距

微波光学与布拉格衍射是近代物理实验的重要内容[1]. X射线布拉格衍射实验，技术含量高，自动化程度高，但也存在不足：成本高，学生的参与度低，对实验仪器各部件了解不足[2]. 而在微波布拉格衍射实验中，3 cm固态微波源易获取，模拟晶体结构可调节，整个仪器结构组成简单. 微波波长在0.001～1 m之间,X射线波长介于0.001～10 nm之间,微波的波长远大于X射线，用微波模拟X射线的布拉格衍射实验，可以得到肉眼可视的模拟晶格，即将现象从微观尺度放大到宏观尺度. 因此有利于学生对X射线在实际晶体布拉格衍射的了解和认知.

早在1981年天津大学的应广寿等[3]使用向量叠加的办法，推出了布拉格衍射峰的位置并解释了衍射图中次级峰出现的原因. 俞书乐等[4]制作了底心立方模型，观察到消光现象. 2006年起，可检索到国内刊物发表的微波单缝及布拉格衍射相关论文有十余篇，例如，文献[5]证明了入射波一定时衍射极大由晶面间距决定；文献[6]介绍了微波单缝衍射实验中出现的畸变现象；文献[7]设计了线阵模拟晶体，能有效地调节晶面间距；文献[8-9]讨论了布拉格定律的衍射级数与微波波长的关系及实验测量系统的改进. 柳艳等[10]测量发现体心立方的衍射峰强度比简单立方的衍射峰强度明显增加，但文献中未给出模拟晶体的点阵参量及各晶面如何同时测量等细节；刘强春等[11]改变模拟晶体的实际位置，研究了模拟晶体位置对布拉格衍射峰位置的影响. 另外，文献检索发现国外学者也对微波布拉格实验进行了深入研究或对仪器设备进行了改进，值得国内同行参考和借鉴，相关内容可参考文献[12-14].

考虑到简单立方结构的晶体非常罕见，本文在研究简单立方模型的基础上，进一步探讨四方、体心立方及底心立方等不同晶体模型的微波布拉格衍射实验. 实验中观察到了体心立方和底心立方模型(100)面的消光现象，并在向量模拟方法确定衍射峰的位置[3]基础上，推导了多层晶体的模拟公式.

1 实验原理及方法

1.1 微波布拉格衍射实验原理

在微波布拉格衍射实验中，仿照X射线衍射与真实晶体的相互作用关系，以微波代替X射线，以晶格常量与微波波长相近的模拟晶体代替真实晶体，用微波照射模拟晶体，得出从不同晶面的格点上反射的微波产生干涉应该具有的条件，即布拉格衍射条件：

2dsinθ=nλ,n=1,2,…，

(1)

其中，d为面间距，θ为掠入射角，λ为微波波长，n为衍射级数.

1.2 实验仪器和晶体模型

实验采用北京大华无线电仪器厂生产的DHMS-1微波分光仪． 3 cm固态微波发射源提供波源，它是由固态信号发生器生成与所需微波频率相同的电流，而后由喇叭口天线发出具有平面波面的微波，经过中间的实验仪器后，到达接收喇叭天线再将微波强度信号转变成电流信号，电流信号由微安表读出.

点阵常量为4 cm简单立方模型由5×5×5共125颗小金属球组成，将每条横线上的小球等间距排列好，前后上下一致，可以逐层调节，先粗调后细调. 四方模型实际就是原来的简单立方模型，调节微波入射方向的(100)晶面间距，由简立方调节成四方(a≠b=c)，a可以2～5 cm变化，b=c=4 cm保持不变． 体心立方和底心立方模型是在4 cm简单立方模型的基础上添加位于体心64颗金属球或底心的80颗金属球. 实验中采用9 mm尼龙线作连接线，白色棉线用于给小球提供足够的摩擦力使之不易滑动，在木框架打孔，用于给位于体心的金属球提供连接线固定位置，最后组装成点阵常量为4 cm体心立方和底心立方模型.

2 实验探究

2.1 简单立方的峰位模拟和实验检验

简单立方的模拟晶体的晶格常量a=4 cm，微波源波长3 cm固定不变. 在测定(100)晶面的衍射强度分布图时，选取合理的入射角20°～70°，法线和入射角组成的平面与(100)晶面相互垂直，且法线始终在另一个与被测(100)晶面相互垂直的(010)面内，测量(100)面随掠入射角θ变化的衍射波强度，可得到(100)面和(200)面的衍射峰. 同样(110)面和(120)面与(100)面存在固定夹角，只是比(100)面的操作多一步，即事先转动固定的角度差. 对于简单立方(110)面，固定角度差是45°，(120)面与(100)面的固定角度差是25.6°.

A1=cos 2φ,A2=cosφ，A3=1,

A4=cos (-φ),A5=cos (-2φ),

(2)

合向量为

A=A0(1+2cos 2φ+2cosφ)，

(3)

强度正比于振幅的平方值，因此

I=I0(1+2cos 2φ+2cosφ)2.

(4)

图1 矢量合成示意图

实验中，简单立方的(100)面的1级衍射强于2级衍射，是因为微波在晶面间进行了多次衍射，最后结果是多次衍射结果的叠加. 列出前5层的晶体模型的模拟公式组：

(5)

(6)

实际上，由125颗金属球构成的5×5×5晶体模型包含着4×4×4晶体模型、3×3×3晶体模型、2×2×2晶体模型和1个小球晶体模型，其衍射图中必然有这些晶体模型的组分． 取各组分的比例因数均为0.5，各层的向量如上，则总合向量为

A=A0(6.562 5+10cos 2φ+12.5cosφ+

5cos 1.5φ+6.25cos 0.5φ).

(7)

所以简立方(100)晶面衍射强度模拟公式为

I(100)=I0(6.562 5+10cos 2φ+12.5cosφ+

(8)

同理，得到简立方(110)和(120)晶面衍射强度模拟公式：

I(110)=I0(8.062 5+2cos 4φ+5cos 3φ+

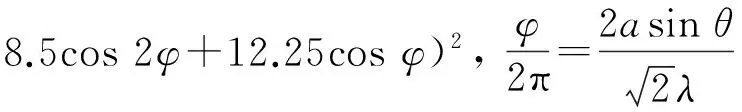
(9)

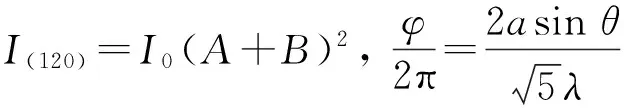
(10)

A= 3.312 5+2cos 6φ+2cos 5φ+cos 4.5φ+

4cos 4φ+4.5cos 3φ+cos 3φ,

B= 2cos 2.5φ+6.5cos 2φ+6cosφ+

2.25cos 1.5φ+2.25cos 0.5φ.

由以上公式绘图，取θ为20°～70°，就可得到简立方3个主要晶面模拟图.

图2给出了4 cm简立方3个主要晶面(100)，(110)和(120)衍射的模拟图与实验图. 通过比较模拟和实测结果可以发现(100)面的衍射峰和(200)面的衍射峰的位置合理，并且2个峰的强度也比较合理. 然而(100)面强度明显大于(200)，是因为散射波在反射路程中部分被其他金属球再次散射到其他方向，路程越远，强度越小． 这说明微波在晶格中衍射有多次散射，最终结果是多次散射的复合结果. (110)面的衍射峰的峰位在32°，(120)面的衍射峰的峰位在57°，拟合比较好，对次级峰的拟合也比较好. 次级峰是由各晶面的子散射波叠加而来的，可以由拟合式(8)～(10)计算出. 目前理论模拟图中的各曲线可解释各晶面的多次衍射强度相对强弱及次级峰出现位置，但各晶面的衍射峰相对强弱取决于晶体模型的大小、点阵金属球数以及晶面间距等多种因素，图2(a)只能给出相对强度的变化趋势.

(a)模拟图

(b)实验图图2 4 cm简立方3个主要晶面衍射的模拟图与实验图

将晶体的晶格常量增加为a=5 cm，取θ为20°～70°，绘出(100)晶面的模拟图和实验图． 结果表明：图3(a)的37°和64°主峰，分别对应(200)和(300)晶面，图3(b)在37°和62°处出现这2个主峰，分别与它们相对应，在23°，26°和30°附近出现次级峰，而(100)峰位小于20°，微波可能直射部分而未被测量到；在25°和57°出现2个衍射峰，分别对应(110)和(220)晶面，这与理论值的25°和58°基本吻合.

比较图2和图3，可观察到晶面间距变大衍射峰向低入射角方向移动；选择较大的晶面间距(如5 cm)，可观察到(100)晶面的2级和3级衍射峰，及(110)晶面的1级和2级衍射峰. 采用有限点阵向量叠加模拟结果与实验数据一致，可解释相对衍射峰的强度变化和次级峰出现的位置.

(a)模拟图

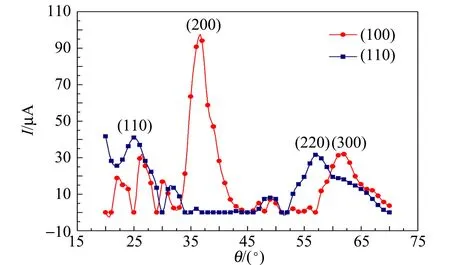
(b)实验图图3 5 cm简立方(100)和(110)面衍射的模拟图与实验图

2.2 四方模拟晶体峰位变化规律

在本次实验中，波长不变，模拟点阵可以由简立方调节成四方(a≠b=c)，a可以从1～5 cm变化. 当a较小时，小球大小不可忽略，在间距a大于小球的直径2 cm时，测量误差较小. 模拟晶体在水平面中的面指数表示为(hk0)，则面间距可表示为

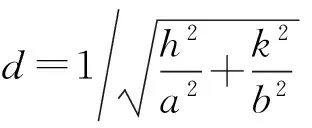
(11)

代入布拉格公式，得到：

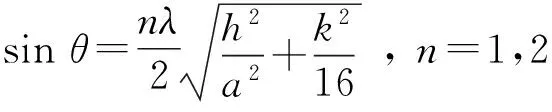
(12)

实验中θ角从20°开始，到仪器极限74°，因此0.34≤sinθ≤0.96.

当n=1，λ=3时，对于四方晶体的间距为a的(100)面，计算可得1.56≤a≤4.39，在此范围内可以得到(100)晶面的衍射峰；对于(110)晶面，要想看到峰，则a≥1.70；同样，对于(120)晶面，1.59≤a≤5.25；对于(210)晶面，a≥0.42.

当n=2，λ=3时，对于四方晶体的间距为a的(200)面，计算可得3.12≤a≤8.77;对于(220)晶面，要想看到峰，则3.58≤a≤6.23. 同样，对于(240)晶面，a≥3.40；对于(420)晶面，a≥1.25.

当n=3，λ=3时，对于四方晶体的间距为a的(300)面，计算可得4.68≤a≤13.19;对于(330)晶面，没有合理范围，所以在本次实验不可能找到(330)的衍射峰. 事实上，如果晶面间距太大，衍射峰强度太弱，实验上也观察不到.

结合2≤a≤5，获得本次实验可以得到的衍射峰和四方晶体中可变值a的允许范围见表1.

表1 四方晶体中点阵参量a的允许范围

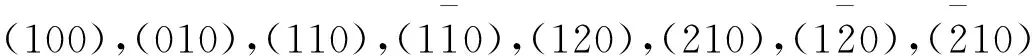
对比a=3.5 cm的四方模型的(100)，(110)晶面，a=4.0 cm的四方(简立方)模型的峰位发生移动. 对于a=4.8 cm的四方的(100)晶面出现2次与3次衍射，衍射强度分布图在39°和70°，分别是(200)面和(300)面的峰位. 作3种四方模型的峰位比较图4，可发现(100)晶面和(200)晶面的衍射峰随间距变大而向低掠入射角方向移动，因为2级峰在1级峰后侧，所以间距增大到一定程度时，(100)衍射峰会先行移出20°角外侧而消失. 类似地，四方晶体模型(110)晶面的衍射峰随间距变大而也向低掠入射角移动，而在3种四方晶体模型中(010)的峰位始终不变，保持在22°位置，因为b=4 cm，(010)晶面间距保持不变.

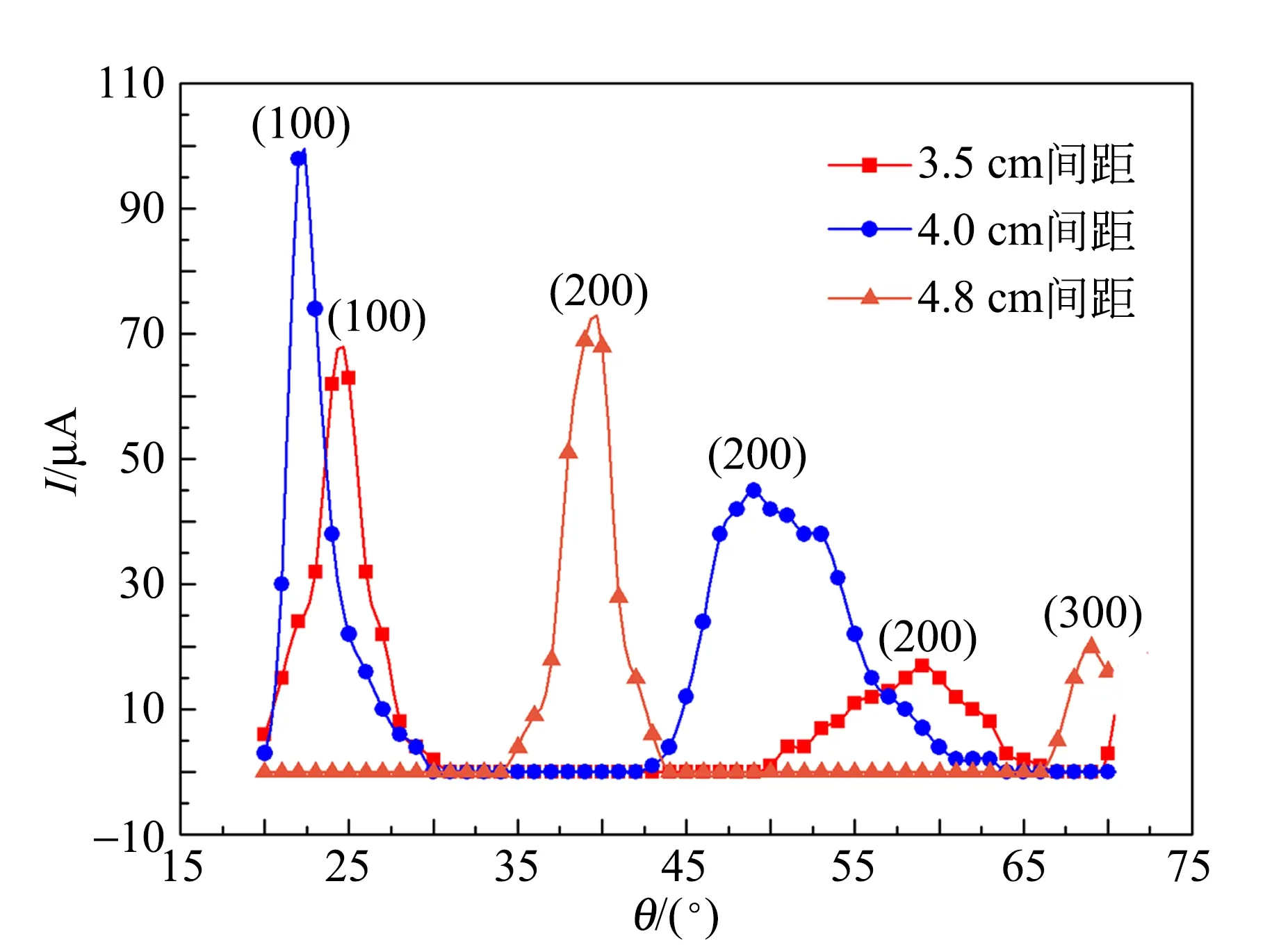
图4 3种不同间距四方模型的峰位

2.3 体心立方和底心立方的衍射强度分布和消光现象

由固体物理学基础知识可知[15]，对于体心立方结构，晶胞中的2个相同的原子位于(0,0,0)和(0.5,0.5,0.5)，则衍射波的强度可表示为

Imh,mk,ml∝f2[1+cos π(nh+nk+nl)]2+

f2[sin π(nh+nk+nl)]2.

(13)

式中f是散射因子，n是衍射级数. (13)式表明，衍射图中找不到衍射面指数和(nh+nk+nl)为奇数的衍射斑，故(100)的峰位将消失或被有效减弱.

同理，对于底心立方结构，晶胞中的2个相同的原子位于(0,0,0)和(0.5,0.5,0)，则衍射波的强度可表示为

Imh,mk,ml∝f2[1+cos π(nh+nk)]2+

f2[sin π(nh+nk)]2.

(14)

(14)式表明：衍射图中找不到衍射面指数和(nh+nk)为奇数的衍射斑，故其(100)的峰位也将消失或被有效减弱.

图5给出点阵常量为4 cm的简单立方、体心立方和底心立方3种不同晶体模型(100)面衍射强度分布. 从图中可以看出，对比简单立方，体心立方衍射图中原有的(100)晶面衍射峰被消光，而(200)晶面衍射峰仍存在，并且比简单立方的更陡，微波的散射波更强，这符合体心立方模型的(200)面的层数以及体心立方模型中参与衍射的金属球都多于简单立方的实验事实.

图5 简立方、体心立方和底心立方(100)面衍射峰比较

同样，底心立方的(100)衍射强度分布类似于体心立方，在其衍射图中(200)晶面的峰位在49°，而(100)面由于被消光而未出现. 另外，实验也证实(110)晶面衍射峰未出现消光，且观察到(120)晶面也存在消光现象.

3 结 论

立方晶体实验满足布拉格衍射规律，晶面间距变大衍射峰向低入射角方向移动；选择较大的晶面间距(如5 cm)，可观察到(100)晶面的2级和3级衍射峰，以及(110)晶面的1级和2级衍射峰. 采用有限点阵向量叠加模拟计算结果也与实验测量数据一致，可解释相对衍射峰的强度变化和次级峰出现的位置. 四方晶体比简单立方更复杂，详细分析了四方晶体模型不同晶面的衍射峰随晶面间距的变化规律，并示例实验证实四方与简单立方的异同. 体心立方和底心立方模型的衍射实验中观察到衍射消光现象，即(100)晶面的衍射峰被明显减弱. 揭示了微波布拉格衍射中随着晶体结构类型和结构参量变化而引起的衍射峰强度和位置的变化.

[1] 吴思诚，王祖铨. 近代物理实验[M]. 北京:高等教育出版社，2005：292-297．

[2] 吕蓬，廖坤山，陈宏斌. 布拉格衍射实验的类比教学研究[J]． 淮北师范大学学报(自然科学版)，2014，35(4)：84-87．

[3] 应广寿，李华，肖家鑫，等. 用微波的布拉格衍射测定模拟晶体的晶格常数实验简介[J]. 物理实验，1981，1(2)：41-44，69．

[4] 俞书乐，汪家友. 微波布拉格衍射实验内容的扩充和设备的改进[J]. 物理实验，1987，7(6)：241-243．

[5] 康伟芳，薛玉春，刘帅. 布拉格衍射及其应用[J]. 大学物理实验，2006，19(2)：11-14．

[6] 霍伟刚，程世红，王秋薇. 微波单缝衍射实验中的畸变现象研究[J]. 物理实验，2008，28(9)：1-4．

[7] 侯林利，章志敏，周小红，等．一种新型模拟晶体的设计[J]. 大学物理实验，2010,23(2):12-15．

[8] 何颖卓，李春芝. 微波布拉格衍射实验中测量衍射极大值的新方法[J]. 大学物理实验，2013，26(5)：9-12．

[9] 徐春阳，陈文婷，王晓栋，等. 微波布拉格衍射中立方晶体晶面衍射测量与模型选取讨论[J]. 物理实验，2014，34(10)：45-48．

[10] 柳艳，王旗，朱盼盼，等. 简立方晶体与体心立方晶体的微波布拉格衍射比较[J]. 大学物理实验，2013，26(增)：4-5．

[11] 刘强春，花宁，尹新国. 微波布拉格衍射实验中模拟晶体位置选取的讨论[J]. 吉林师范大学学报(自然科学版)，2006(1)：78-80．

[12] Cornick M T, Field S B. Microwave Bragg diffraction in a model crystal lattice for the undergraduate laboratory [J]. American Journal of Physics, 2004,72(2):154-158.

[13] Amato J C, Williams R E. Rotating crystal microwave Bragg diffraction apparatus [J]. American Journal of Physics, 2009，77(10)：942-945.

[14] Yuan C P, Lin S Y, Chang T H, et al. Millimeter-wave Bragg diffraction of microfabricated crystal structures [J]. American Journal of Physics, 2011,79(6):619-623.

[15] 陆栋，蒋平，徐至中. 固体物理学[M]. 上海：上海科学技术出版社，2010:7-8.

[责任编辑：任德香]

Microwave Bragg diffraction of different macroscopic crystal models

ZHENG Hang, WU Yi-chu, YANG Wei， LIU Hai-lin, LI Mei-ya

(Experiment Teaching Center for Physics, Wuhan University, Wuhan 430072, China)

The rules of microwave Bragg diffraction under different macroscopic crystal models were investigated. Experimental results showed that 2nd- and 3rd-order diffraction peaks appeared in simple cubic (100) plane when choosing larger plane spacing (e.g 5 cm). The relationship between the position of diffraction peaks and the spacing of different crystal planes was analyzed by adjusting simple cubic model into tetragonal crystal model. Both body-centered and base-centered cubic models were exquisitely designed and constructed, the extinction phenomenon of the (100) crystal plane was observed. Finally, the results simulated by the interference of the scattered waves from limited lattice points were in good agreement with the measured data.

microwave; Bragg diffraction; crystal model; plane spacing

2016-07-04

国家自然科学基金资助项目(No.J1210061);湖北省及武汉大学教学改革研究项目(No.JG201429)

郑 航(1993-)，男，福建平潭人，武汉大学物理科学与技术学院2012级本科生.

吴奕初(1964-)，男，福建上杭人，武汉大学物理科学与技术学院教授，博士，主要从事正电子湮没技术在材料科学中的应用研究和近代物理实验教学工作.

O436.1

A

1005-4642(2017)03-0006-05