驻波法测量声速实验的探讨

邵维科，赵 霞，轩植华

(1.中国科学技术大学 a.少年班学院； b.物理学院，安徽 合肥 230026)

学生园地

驻波法测量声速实验的探讨

邵维科a，赵 霞b，轩植华b

(1.中国科学技术大学 a.少年班学院； b.物理学院，安徽 合肥 230026)

通过建立起声波无限次反射的模型，对用驻波法测量声速实验的原理进行探讨. 利用该模型拟合实验结果、分析实验数据和现象，揭示了理论的合理性及尚存的局限.

声速；驻波；无限次反射

声速测量作为大学物理实验的基础实验，在许多教材[1-4]中都有出现，在一些具体的实验题目设计中也有涉及[5]. 在阐述声速测量的实验原理时，尽管有些教材[4]给出了正确的电压-接收与发射换能器位置关系图，但均简单地解释为发射换能器发射的声波和接收换能器反射的声波叠加形成驻波，接收器接收到的是驻波在接收器位置的声压. 很多文献[6-9]都对这模型提出了质疑，该模型的缺陷在于其中反射波方程隐含了假设，即反射面在原点，而实际上反射面是在换能器面上. 基于声波在两换能器面间无限次反射叠加的构想，建立了更完善的模型，并对模型进行了验证.

1 驻波模型的缺陷

在媒质中传播的声波有3个基本变量：声压相对于静态的增量p、介质微元微振动的速度u、介质的密度相对于静态的增量ρ. 为方便起见声学理论将p称作声压，把ρ称作密度增量. 这里介质微元指的是流体力学中常用的包含一定量介质粒子，宏观上足够小、微观上足够大的介质块.

对于空气中的声波，若它的3个基本变量只依赖于直角坐标(称这种声波为一维声波)，则在线性近似下，这3个变量互成比例，即

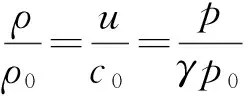
(1)

其中ρ0为空气密度，c0=γp0/ρ0为空气中的声速，γ=cp/cV为空气的比热容比，p0为大气压. 定义声阻抗率Z为声压p与速度u之比，在空气中，Z=p/u=ρ0c0.

测量波长所利用的驻波模型建立在一维、线性声波的假设基础上，适用上面的定义和公式. 发生器发出的是时谐波，其声压满足

p+(x,t)=P0ei(kx-ωt),

(2)

式中+表示正向传播，P0为声压的幅度，初相位设为0.k为声波的角波数，ω为声波的角频率，二者满足

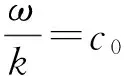
(3)

平面声波，即一维时谐声波在反射和折射时满足入射角等于反射角；入射角i和折射角r之间遵循Snell定律，即

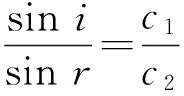
(4)

其中c1和c2分别为2个介质中的声速.

若两介质间的声阻抗率之比为

z=Z1/Z2,

(5)

则界面上的折射、反射声压与入射声压之比，即声压透射系数T、声压反射系数R满足

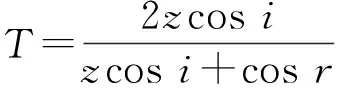
(6)

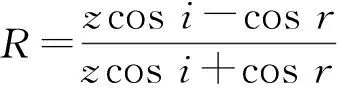
(7)

垂直入射时，i=r=0，(6)～(7)式化为

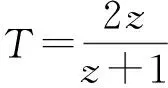
(8)

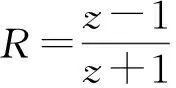
(9)

文献[1]给出的反射波表达式为

p-(x,t)=P0e-i(kx+ωt),

(10)

从而p+和p-叠加形成驻波，其在接收器面xr处的取值为

(11)

教材原式用空气微元的微振动振幅来表征声波，这里为统一起见用振幅和声压的关系将其改写成声压式，不失其意.

(2)式和(10) 式中无衰减，意味着空气的声阻抗率为实数，则应有

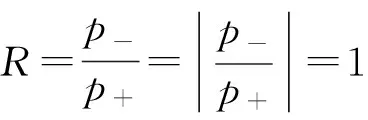
(12)

由 (9) 式

z→∞ ,

(13)

这里，z特指换能器与空气间的声阻抗比，表明换能器反射面为理想反射面. (10)式实际上蕴含了换能器声阻抗率非常大，换能器面上发生完全的反射这一假设.

(12)式仅对理想反射面才成立，由该式可以计算反射面位置x0

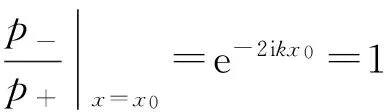
(14)

又由(10)式中初相位为0，可得

x0=0 ,

(15)

即反射面在原点处. 但是事实上反射面为接收器面，即x0=xr，两者显然矛盾. 若考虑x0变化带来的影响，则(10)式可以修改为

p-(x,t)=P0e-i(kx+ωt-δ),

(16)

注意到 (12) 式仍成立，故

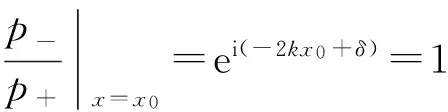
(17)

即

δ=2kx0,

(18)

p-(x,t)=P0e-i(kx+ωt-2kx0),

(19)

从而接收器面上的压强也要做出修正. 由(8)和(13)式得

T=2 ,

(20)

故

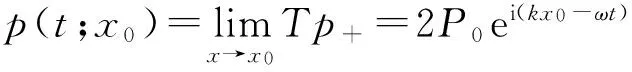
(21)

声速的测量实验中，一般用接收器在不同位置处的声压幅度来求得声压变化的周期[1-4]，而由(21)式，声压在各处的幅度都为2P0，与接收器位置无关. 这个预言不符合声压幅度周期性变化的实验现象，无法获得波长.

2 无限次反射形成叠加声场

上文已经阐明，仅靠发射波p+和1次反射波p-叠加形成的声场无法得到与实验相符合的预言，但是可以设想，声波并不会在第1次反射后就传向无穷远处，而是会遇上发射器面发生第2次反射，进而遇上接收器面发生第3次反射……直至无穷. 显然，若按照上文中往返2次波叠加的驻波模型的假设，换能器声阻抗极大、发生完全的反射且介质无衰减，则无限次反射叠加的结果必然是声压趋于无穷. 为使声压收敛于有限值，必然要考虑介质的衰减和反射的损失(如换能器尺寸有限)，即声波在空气中的角波数不再是实数k，而是复数κ=k+iη，其中η的物理意义为声波的衰减系数，并且换能器和空气间的声阻抗比z和声压反射系数R也变为复数. 但是衰减和反射的损失在1次反射中非常小，即应有

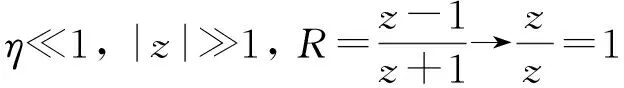
(22)

为表述清晰，不妨按产生顺序记第1次来波、第1次回波、第2次来波……为第1，2，3……列波. 则接收器处接收到的第n+2列波的声压pn+2(t;x0)相对于第n列波的声压pn(t;x0)相位落后2κx0，振幅变为R2倍，即以下递推式

pn+2(t;x0)=pn(t;x0)R2e2iκx0,

(23)

由(2)式，第1列波在接收器处的声压为

p1(t;x0)=P0ei(kx0-ωt),

(24)

则第2列波的声压为

p2(t;x0)=Rp1,

(25)

接收器处总声压为

Peffei[φ(x0)-ωt],

(26)

由于测量量是示波器上信号的幅度，相位φ(x0)-ωt表示信号图像的左右移动，可以舍去不计. 记剩余部分为有效声压peff，则

peff(x0)=Peff=|1+R|P0(1+

|R|4exp (-4ηx0)-2|R|2exp (-2ηx0)·

cos (2kx0+2argR))-1/2.

(27)

从(26)式可以看到，无限次反射叠加的声波在两个换能器之间形成了复杂声场，既非行波也非驻波. 而有效声压peff确实以λ/2为“周期”，所以教材中往返2列波叠加的驻波模型能得出正确的波长，是因为它恰好和有效声压具有同样的周期性.

为了进一步考察有效声压peff的性质，考虑cos (2kx0+2argR)=+1/-1处，注意到η≪1，因此

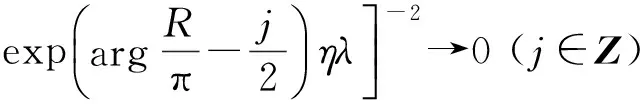
(28)

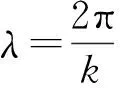
故这2组位置可以近似看作图线的极大值点和极小值点，因而

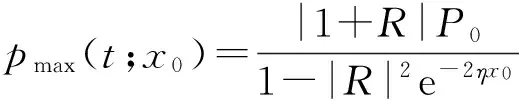
(29)

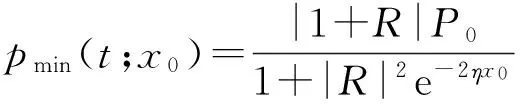
(30)

又由 (22) 式

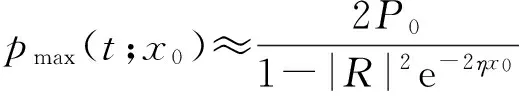
(31)

pmin(t;x0)≈P0.

(32)

即峰值随接收器右移而减小，谷值基本不变. 后面的实验结果基本支持了此结论.

3 实验对理论的检验

使用SV5型声速测量仪进行了多次实验，图1给出了其中某次测量的典型结果. 可以利用Mathematica软件，用式 (27)拟合数据. 但是由于测量的区间处在 (27) 式的中段，没有精确地确定x0=0的位置，故拟合时必须对零点作修正. 另一方面，示波器的电压示数和实际的声压间有一转换比α，故实际使用的拟合公式为

Vmeas(x0)=αpeff(x0+ξ)=

α|1+R|P0(1+|R|4exp [-4η(x0+ξ)]-

2|R|2exp [-2η(x0+ξ)]·

cos [2k(x0+ξ)+2argR)]-1/2,

(33)

式中ξ为零点漂移量.

拟合时确保|R|<1，即声波反射时一定是衰减的，并且固定波长λ为实验图像中各峰最高点间距均值的2倍，拟合参量为|R|，α|1+R|P0，η，ξ，argR. 共做2次拟合：第1次拟合时固定|R|=1，令其他4个参量的初始值为0，可以得到这4个参量的初次拟合值；然后以4个初次拟合值为初始值，并且使|R|的初始值稍小于1，再次拟合得到全部5个参量的最终拟合值. 表1为4次测量的拟合参量，图1为实验数据和拟合曲线.

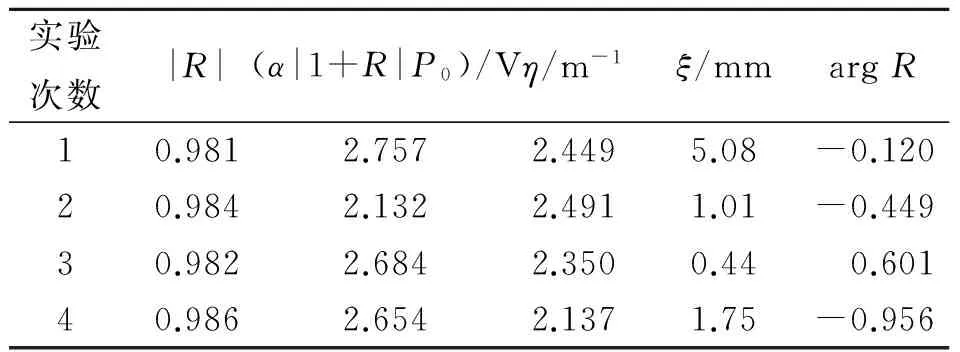
表1 各参量拟合值

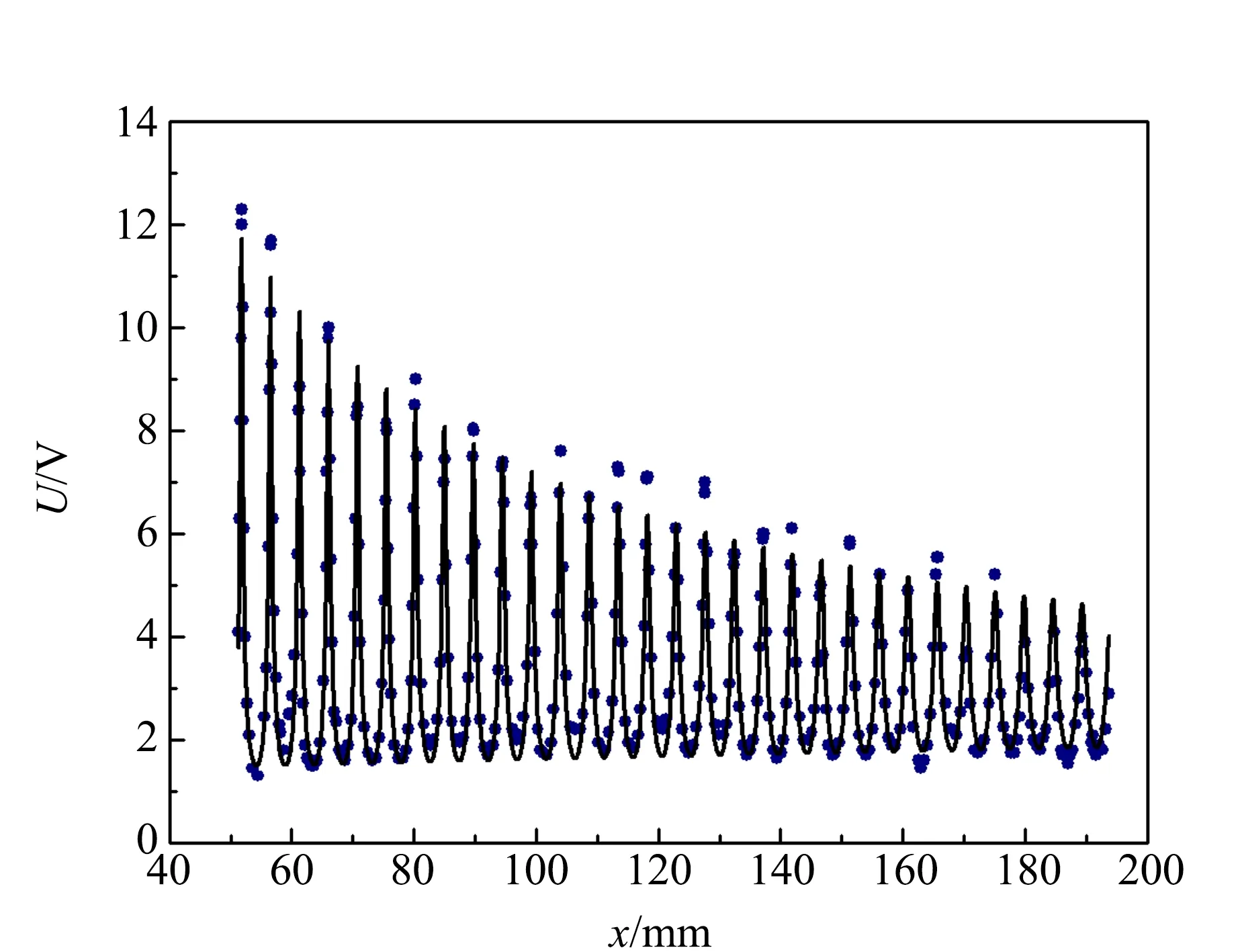
图1 实验测量(表1中第4次)与拟合结果

在拟合过程中可以发现，令|R|=1后得到的其他4个参量的初次拟合值在较大的初始值范围内都收敛到同一组值上；而再次拟合时|R|的初始值即使有很小的变化也会导致收敛到的最终拟合值不同. 这点从 (33) 式也显见，常量ξ和R不独立，可以被归入到|R|和argR中，这就导致数值可以在这几个常量之间有一定的自由分配，所以通过拟合无法得到这几个数的实验值，只能通过其他实验事先确定|R|或argR，才能得到剩下2个常量的值. 拟合结果中ξ和argR有较大误差正是此原因.

从图1可以发现，总体上来看，拟合曲线和实验数据点的变化趋势互相吻合，尤其是二者的周期性符合得相当好.

但是仍有一些实验结果理论模型不能解释，例如图像的“峰”和“谷”处有一部分符合得很好，另一小部分有一定的差距.

其次，从表1可以发现，α|1+R|P0的误差不很大，但是按其物理意义，α和|1+R|应是固定常量，而P0比可以用几次测量的标度之比来估计. 由图1，α|1+R|P0之比应约为1.2-∶1∶1.2∶1.2+，而由表1，为1.29∶1∶1.26∶1.24. 可以看到，此处理论与实验的符合程度并不高.

再次，式(28)～(32)成立的前提条件是η≪1，而η的拟合值说明这个条件并不成立. 注意到式 (28) 是拟合时固定波长λ为实验图像中峰间距的2倍的依据，如果该式不成立，则峰的间距和λ/2理论上不相等. 但是在拟合中发现两者之间的差距很小，峰间距仍然是λ/2的很好的近似.

另一方面，仍尚有一些结果用无限次反射的模型不能解释，如图线峰和谷不能完全符合，η≪1条件的不成立，等等. 事实上，进一步的研究可以发现，图线的复杂性中又有一定的规律性. 这将通过进一步做更深入的研究来加以解释.

4 结束语

在整体上实验结果验证了声波在两换能器面间无限次反射的模型，并揭示了周期法测声速的正确性. 实验教材的驻波模型也正是因为和真实声场具有相同的周期性才能得到正确的声速，但是2列波叠加的驻波理论的周期性是建立在不完备的假设基础之上的， 因而无限次反射的模型是更完善的理论模型. 利用该模型，可以对原理类似的实验[10]作出更精细的预言. 事实上，该模型预言在衰减系数η非常小和非常大时的现象有显著的不同，这也等待进一步的计算和验证.

[1] 谢行恕，康士秀，霍剑青. 大学物理实验(第二册)[M]. 2版. 北京:高等教育出版社，2005:11-15.

[2] 袁广宇. 大学物理实验(一级)[M]. 3版. 合肥:中国科学技术大学出版社,2014:76-87.

[3] 柴成钢. 大学物理实验[M]. 北京:科学出版社,2004:131-138.

[4] 王廷兴，郭山河，文立军. 大学物理实验(上册，理工基础部分)[M]. 北京:高等教育出版社，2003:133-137.

[5] 陈建军，龚国斌，高文莉，等. 超声检测综合实验[J]. 物理实验，2016，36(1)：24-27，34.

[6] 缪亚立. 声速测量原理释疑[J]. 物理与工程，2004，14(6):58-60.

[7] 郑庆华. 声速测量实验的探讨[J]. 大学物理，2007，26(9):31-33.

[8] 梁济仁，黄开连. 驻波法测量声速[J]. 广西民族大学学报(自然科学版)，2009，15(3):68-72,101.

[9] 胡险峰. 驻波法测量声速实验的讨论[J]. 物理实验，2007，27(1):3-6,9.

[10] 欧阳丽婷，杨旭东，刘敏蔷，等. 水面波驻波演示仪[J]. 物理实验，2016，36(2)：26-28.

[责任编辑：郭 伟]

Study on sound speed measurement experiment by standing wave model

SHAO Wei-kea, ZHAO Xiab, XUAN Zhi-huab

(a. School of the Gifted Young; b. School of Physical Science,University of Science and Technology of China, Hefei 230026, China)

The standing wave model in sound speed measurement experiment was discussed using infinite reflection model. The new model was validated by fitting the experimental results and analyzing the data and new phenomenon, with which the validity and limitation of it were shown.

sound speed; standing wave; infinite reflection

2016-05-31；修改日期：2016-11-02

安徽省高校省级教学研究重点项目(No.2015jyxm009)

邵维科(1996-)，男，浙江金华人，中国科学技术大学少年班学院2014级本科生.

赵 霞(1973-)，女，四川阆中人，中国科学技术大学物理学院副教授，博士，从事凝聚态物理方向的研究.

O422.1

A

1005-4642(2017)03-0048-04

“第9届全国高等学校物理实验教学研讨会”论文