分析Ⅱ类自发参量下转换光场光子通量分布辅助纠缠源调节

王子逸，王合英，孙文博

(1.中国人民大学 附属中学，北京 100080； 2.清华大学 物理系，北京 100084)

分析Ⅱ类自发参量下转换光场光子通量分布辅助纠缠源调节

王子逸1，王合英2，孙文博2

(1.中国人民大学 附属中学，北京 100080； 2.清华大学 物理系，北京 100084)

分析并测量了405 nm泵浦光产生的Ⅱ类SPDC纠缠点附近小范围内光子通量的空间分布，辅助Ⅱ类SPDC纠缠源调节，从而有助于减少教学实验所需时间，增强学生对纠缠点空间定位理论的理解，有助于学生更好地开展实验学习. 并为对光场进行详细分析以建立程序自动调节纠缠源提供了基础和可能.

量子纠缠；自发参量下转换光场；光子通量；纠缠源

量子纠缠是一种特殊的量子态，它在量子力学中具有极其重要的地位. 量子纠缠的概念最早由薛定谔和著名的EPR样缪提出[1-3]. 量子纠缠的特殊性质使其在量子计算、保密通讯、量子态隐形传送方面具有显著的应用价值[4-6].

自发参量下转换光场(spontaneous parametric down-conversion, SPDC)是单色强泵浦光子流作用于非线性介质时，与量子真空噪声综合作用产生的非经典光场. SPDC光场可用于产生高质量的纠缠光子对，被广泛应用于量子纠缠的研究和应用中. 清华大学近代物理实验室从2009年起开始开展基于Ⅱ类SPDC的量子纠缠教学实验. 教学实验中学生普遍反映收获颇多，但也存在以下问题：对纠缠光子产生机制及纠缠点定位方法缺少深刻的理解，学生对光场分布的理解不够准确，导致实验调节耗时较长[7-8]. 针对以上问题，对Ⅱ类SPDC光场近纠缠点区域小范围内光子通量空间分布进行了理论分析，并利用基于单光子计数器的光子收集系统进行实验测量,辅助搭建双光子偏振纠缠源.

1 理论分析与数值模拟

SPDC过程中1个泵浦光光子转化为1个信号光光子与1个空闲光光子，在一定条件下频率简并的信号光与空闲光光子对具有量子纠缠特性. 基于不同的偏振模式SPDC可分为Ⅰ类和Ⅱ类. Ⅰ类SPDC产生1个偏振相同的光锥，Ⅱ类SPDC产生2个偏振相互垂直的光锥. Ⅱ类SPDC 2个光锥交点处的光子具有偏振纠缠的特性. Ⅱ类SPDC的空间结构及偏振特性如图1所示.

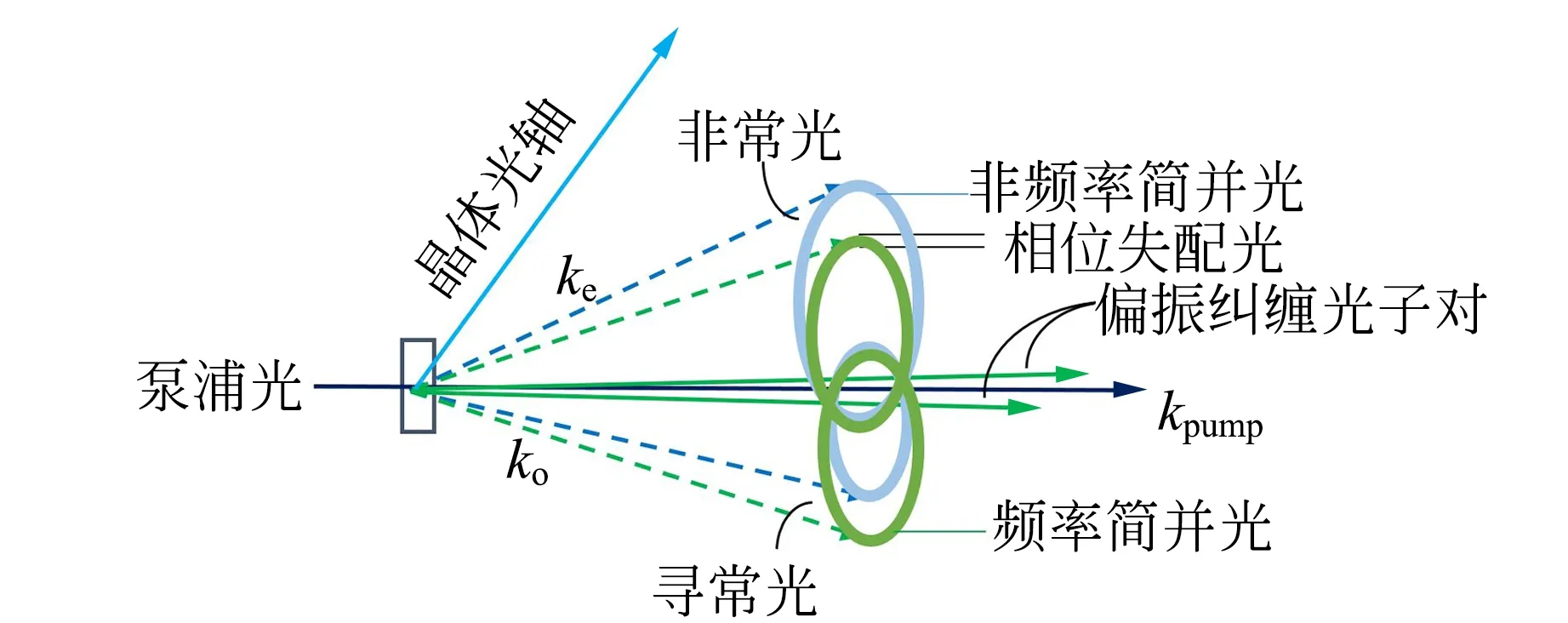
图1 Ⅱ类SPDC光场示意图

SPDC是强泵浦光在非线性介质中与量子真空噪声导致的自发辐射进行参量震荡所产生的. 在这个过程中，泵浦光的能量被耦合进信号光与空闲光中. 信号光与空闲光首先要满足能量守恒，为使产生的信号光与空闲光光强达到最大，也要满足相位匹配，即动量守恒：

ωs+ωi=ωp,

(1)

ks+ki=kp,

(2)

其中ωs,ωi及ωp分别为信号光(signal)、空闲光(idler)以及泵浦光(pump)的频率，ks,ki及kp分别表示信号光、空闲光和泵浦光的波矢.

Ⅱ类SPDC可以产生非频率简并的信号光与空闲光，空间分布可通过(1)～(2)式计算. 在相位失配情况下，即信号光与空闲光波失不符合相位匹配时，信号光与空闲光仍能以较弱的光强产生. 所产生的光强大小与相位失配量Δk相关.

因为Δk是三维矢量，为简化计算，将相位失配量Δk分解为相对于泵浦光的纵向分量Δkz和垂直分量K，定义：

Δkz=kpz-ksz-kiz,

(3)

K=Ks+Ki，

其几何关系如图2所示.

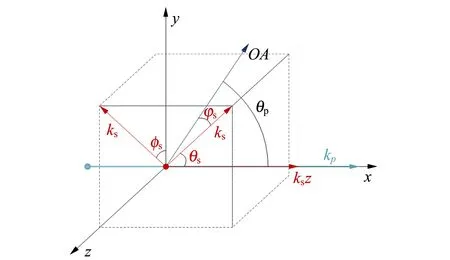
图2 Ⅱ类SPDC几何关系示意图

根据K. Koch等人的计算结果，SPDC光场所产生的单位频率及单位出射角所对应光子通量为[9-10]

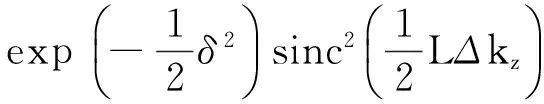
(4)

其中np,ns和ni是泵浦光，信号光与空闲光的折射率，deff是BBO晶体的有效二阶非线性系数，L是作用长度,δ=Kw是信号光与空闲光的无量纲横向动量，w泵浦光半径除以e2.

对于任意的信号光与空闲光光子对，其所处平面与光轴所在竖直平面夹角φs在0°～360°间均匀分布. 而在双光子偏振纠缠源调节过程与光子测量过程中，单光子计数器接收恒定空间角内的光子. 因此当接收器处于光场不同位置时，其接收的光子对应的φs范围也不同. 如图3所示，图中圆环为在相位匹配情况下805～810 nm信号光光子的出射角分布，图中三角区域为一确定的φs所对应的区域. 由于接收器对应的空间角不变，随着接收器逐渐远离泵浦光，其接收范围如图3中长方形区域所示，从中容易看出随接收器与泵浦光距离增大，接收器接收的光子所对应的φs范围变小. 由于光场并非标准圆，此变化关系无法直接计算得到，需要通过理论模拟得出.

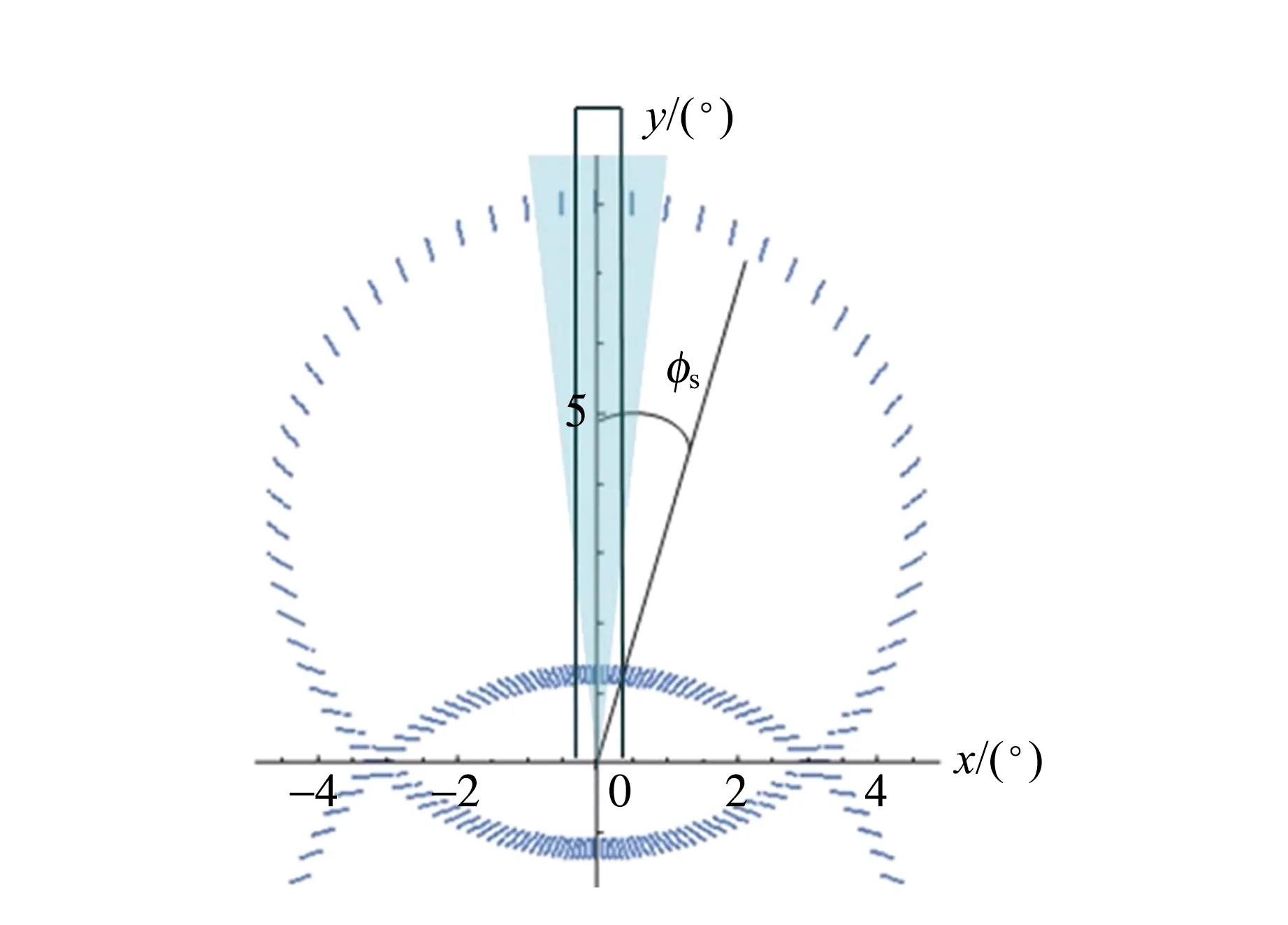
图3 修正因子示意图

基于前文所述，在模拟单光子计数器测量到的光子通量空间分布时需要添加基于光场空间结构的修正因子，用来表示在光场不同位置时单光子计数器接收到的光子对应的φs大小相对值. 修正因子与出射角相关，但基于前文出射角空间分布的计算理论，在相位匹配条件下光子波长与出射角呈一一对应关系，故可以将修正因子转化为与波长相关的因子. 添加修正因子后，(4)式可以写为

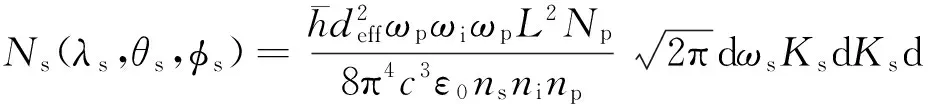
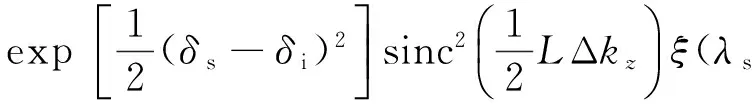
(5)

基于(1)～(2)式，可解得确定波长的信号光出射角，由计算可得在相位匹配条件下，对于确定的φs信号光波长与其出射角具有一一对应关系. 且基于(5)式可以计算得在出射角θs处不同波长的信号光因相位失配产生的光子通量.

故在理论模拟过程中以信号光波长为基础进行遍历，首先计算得到此信号光的出射角，之后将相位匹配光与相位失配光产生的光子通量进行累加，得到此出射角对应的光子通量，遍历完成后得到光子通量的角分布.

模拟得到的信号光与空闲光光锥交点处信号光光子通量空间分布如图4所示. 其中纠缠光子的出射角约为3.0°，而从中可以看出该出射方向上光子通量并不是最大值.

在实际情况中，纠缠光子出射方向为信号光与空闲光光锥的交点，在此处的光子通量为信号光与空闲光通量的叠加. 基于信号光与空闲光空间结构上的对称性，将两者光子通量分别计算并叠加后得到Ⅱ类SPDC光场信号光与空闲光光锥交点处的光子通量空间分布(图5).

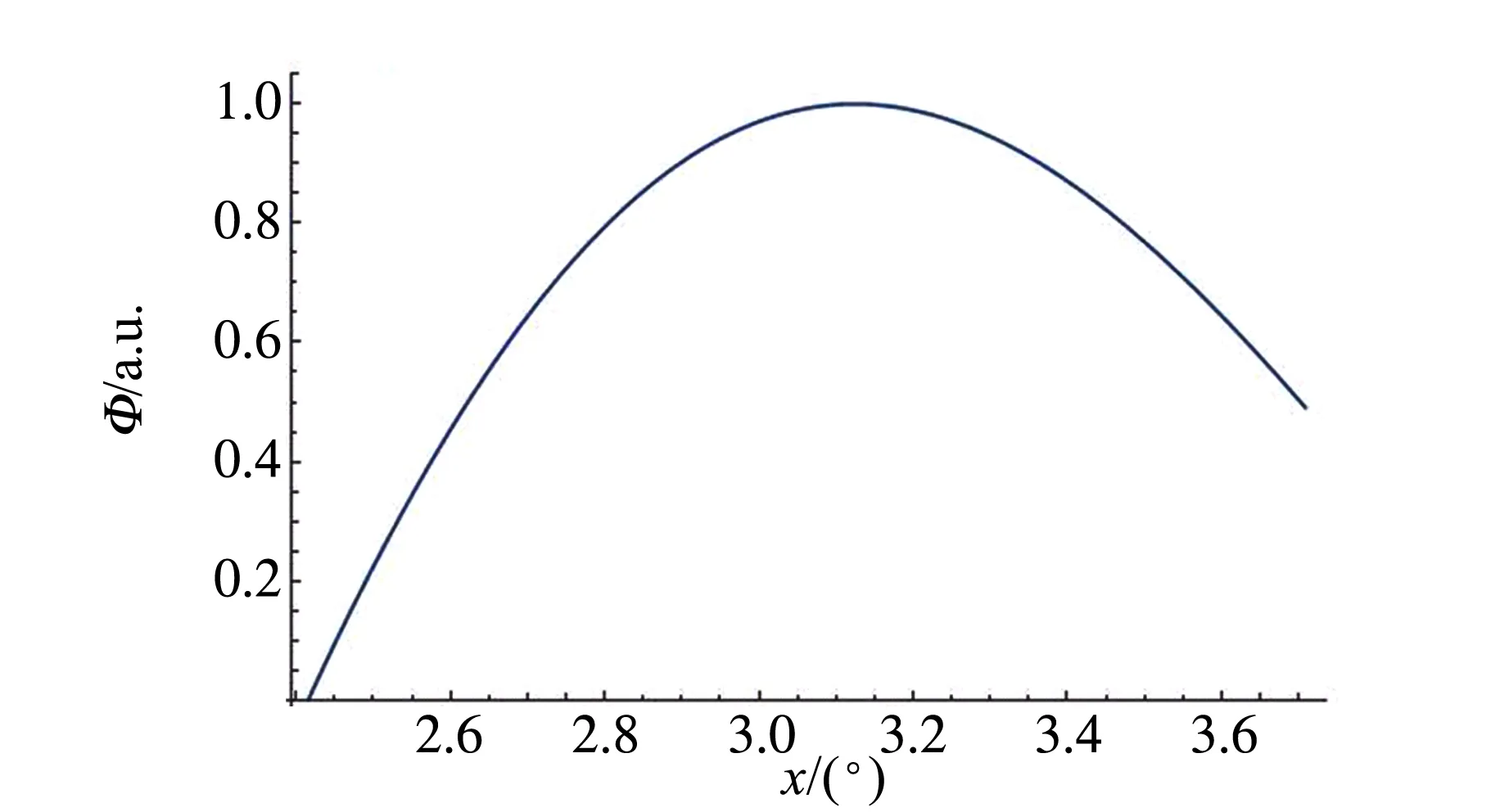
图4 近纠缠点区域信号光通量空间分布

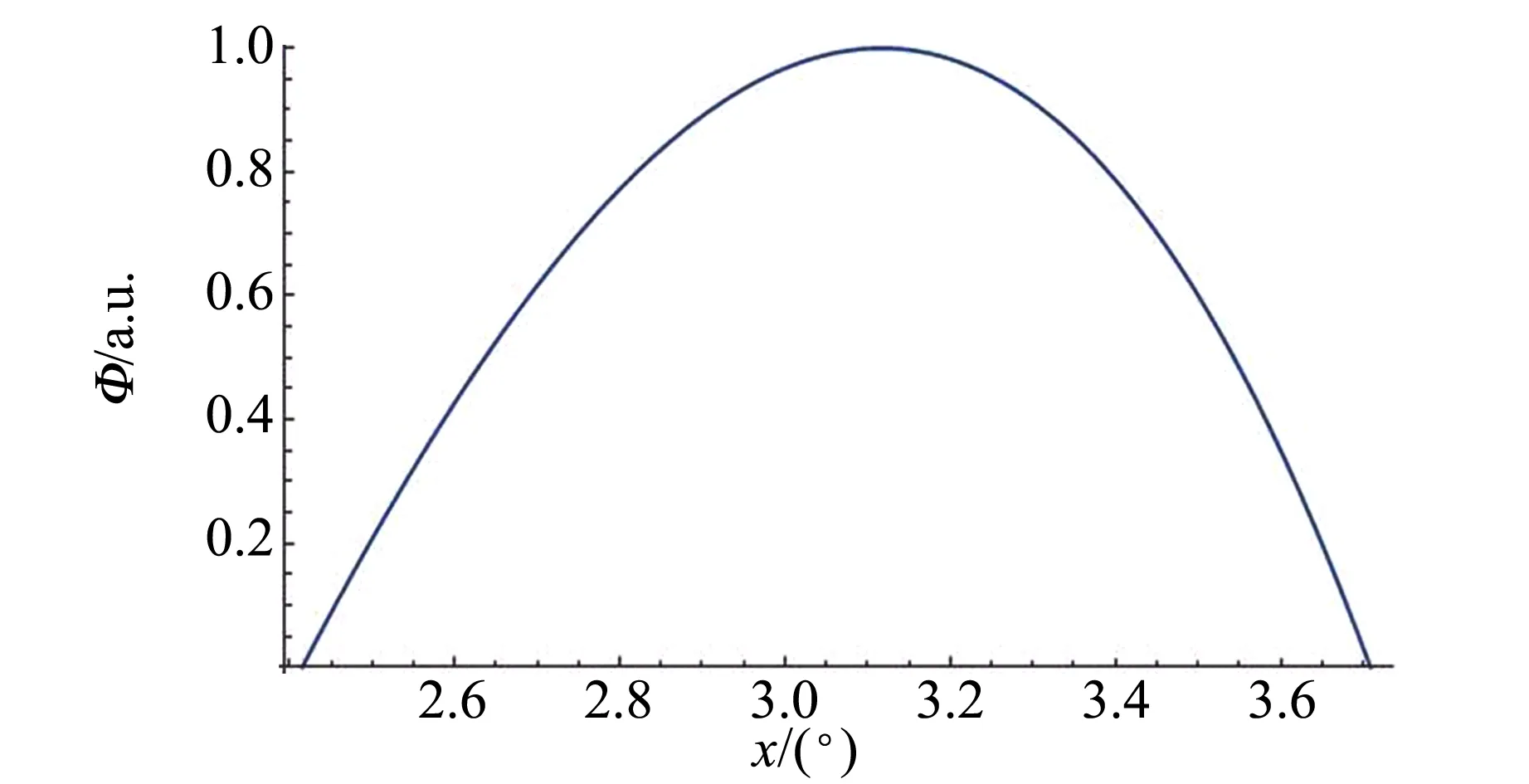
图5 近纠缠点区域光子通量空间分布

2 实 验

本实验中测量Ⅱ类SPDC光场中信号光与空闲光光锥相交区域内光子通量沿水平方向的空间分布. 实验光路如图6所示，通过2个反射镜以调节泵浦光的高度与俯仰，并通过透镜使其聚焦在BBO晶体上. 用尾光接收桶接收透过BBO晶体的泵浦光，防止其干扰测量结果. 光纤准直器固定在可调俯仰角和水平角的移动台上，移动台可以进行竖直方向与水平方向的移动. 光纤一端 连接在光纤准直器上，另一端连接到单光子计数器上，使光纤准直器作为单光子计数器的接收器. 单光子计数器产生的信号进入电子学系统进行处理，再进入计算机系统产生读数.

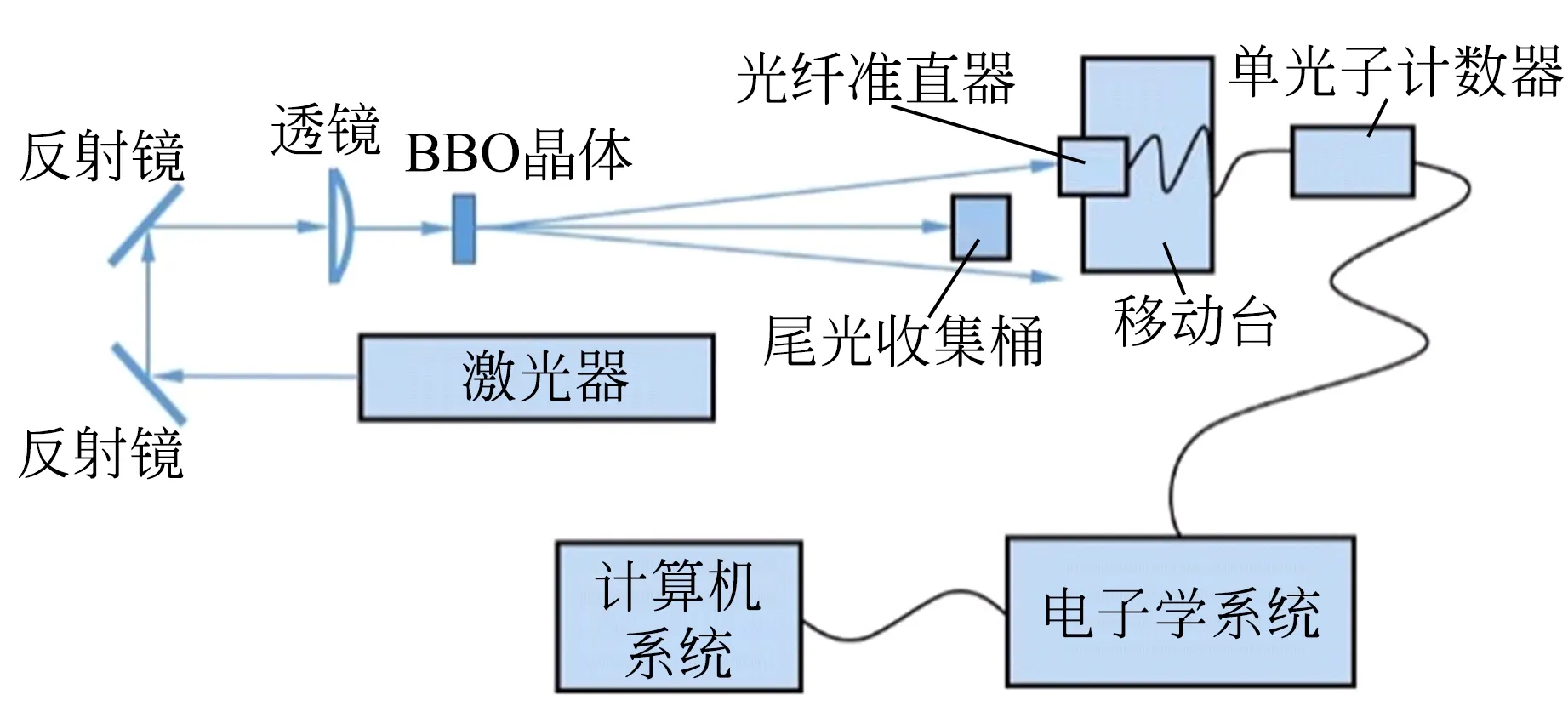
图6 光子通量空间分布测量实验光路图

实验装置如图7所示，BBO晶体晶轴方向在竖直平面内，使信号光与空闲光相交区域处于水平平面内. 首先通过反打光系统将光纤准直器对准纠缠光子的出射方向，并将这个位置作为测量的基准点(在信号光与空闲光相交区域内，频率简并光子即为纠缠光子). 之后沿与出射光垂直的方向以恒定步长进行水平移动，在每个节点调节水平角使得单光子计数器示数最大，并记录最大示数，以此对信号光与空闲光光锥交点处的光子通量进行水平方向的扫描测量. 为了排除背景光的影响，在每个点处旋转BBO晶体90°，并记录旋转晶体前后的示数. 基于理论计算，BBO晶体旋转90°后单光子计数器所对应方向无显著SPDC光场光子通量，所以旋转晶体前后的示数差即为去除背景光后的SPDC光场光子通量.

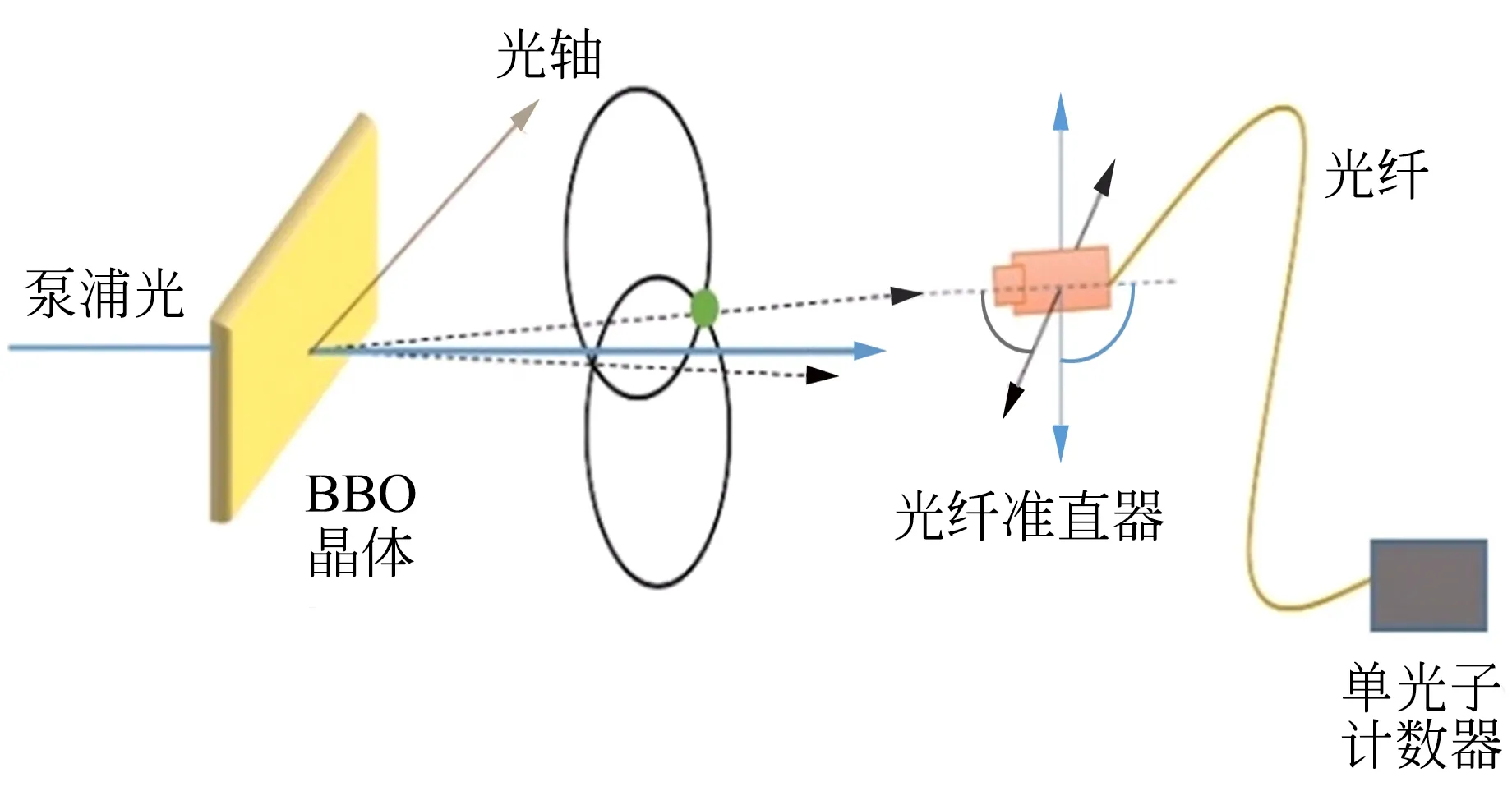
图7 光子通量空间分布测量实验示意图

实验仪器参量：

1)半导体激光器发射激光波长405 nm，线宽0.7 nm，功率18 mW.

2)可见光反射镜反射效率90%.

3)聚焦透镜焦距500 mm.

4)主BBO晶体尺寸7 mm×7 mm×2 mm，切割角度θp=42.6°，光轴在xy平面内与x轴的夹角φ=30°，表面增透膜810 nm/405 nm.

6)单光子探测器(相对)探测效率92%.

7)移动台精度0.01 mm，行程25 mm.

3 结果与讨论

Ⅱ类SPDC光场信号光与空闲光交点处光子通量空间分布的实验测量结果与理论模拟结果如图8所示.

在实验测量中，接收器所在竖直平面距BBO晶体400 mm，所以通过接收器的水平位置来表示光子通量的空间分布. 由于实验中泵浦光准确光强和各元件的反射率等参量的准确值不明，无法准确模拟出光场的光子通量值，故在此讨论光子通量相对值的空间分布.

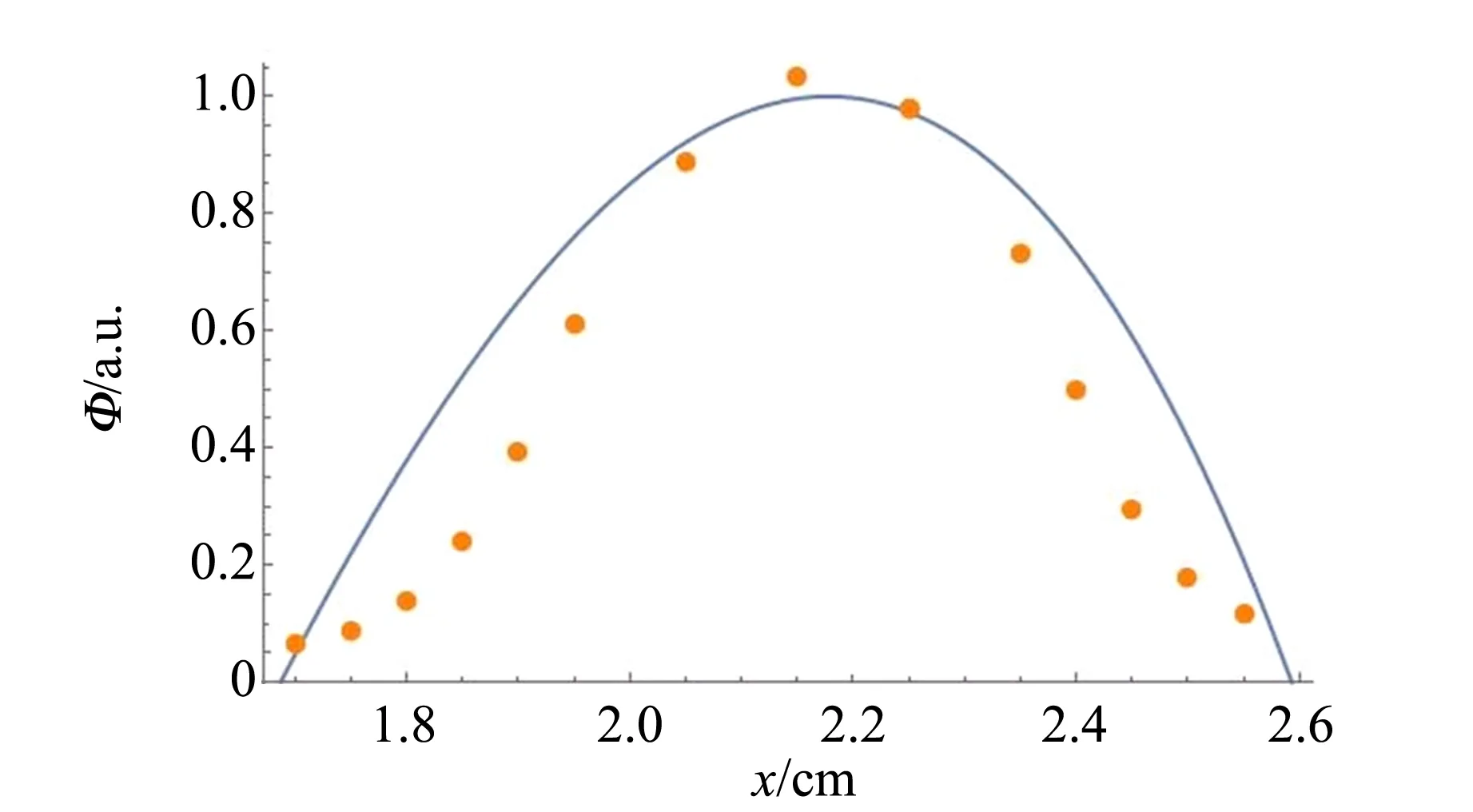
图8 信号光与空闲光交点处光子通量空间分布

由图8可以看出，实验数据与理论数据有一定偏差. 偏差产生的原因是在调节接收器至基准点时竖直方向位置与俯仰角有一定误差， 使得接收器与纠缠光子出射方向距离增大时所测得的光子通量相对于理论结果衰减更快.

图8中2.1 cm处对应纠缠光子出射方向，可以看出在实验中光子通量最大的出射方向与纠缠光子的出射方向有一定偏差. 此偏差是相位失配光以及相位匹配条件下非频率简并的出射光导致的. 但在纠缠源的调节过程中，单光子计数器接收不可忽略的空间角内光子，而纠缠光子出射方向和光子通量最大的出射间的偏差相对较小，所以在调节过程中当单光子计数器示数达到最大时，可认为其已对准纠缠光子的出射方向. 基于这个思路可以有效地辅助学生进行纠缠源的调节，将对纠缠点的定位依据由2个单光子计数器的符合计数转化为了1个单光子计数器单路的计数，简化了对纠缠的定位.

基于以上对于光子通量空间分布的分析，快速地搭建了基于Ⅱ类SPDC光场的双光子偏振纠缠源，并使用CSHS不等式进行验证，实验结果S=2.3，以50个标准差破坏不等式，验证了此纠缠源产生光子对的纠缠特性.

4 结 论

通过计算机模拟得到了纠缠点附近Ⅱ类SPDC光场光子通量空间分布，并使用单光子计数器进行了实验上的验证,促进了学生对SPDC光场空间结构与空间分布的认识，加深了学生对量子纠缠实验现象的理解. 在实验中可应用此结果，从而仅依据单光子计数器单路示数辅助定位光场中的纠缠点位置，辅助双光子偏振纠缠源的搭建，进而降低此类传统纠缠源教学实验的操作难度，提高学生调节纠缠源的效率，减少实验所需要的时间.

[1] Einstein A, Podolsky B, Rosen N. Can quantum-mechanical description of physicalreality be considered complete?[J].Physical Review, 1935,48(10):696-702.

[2] Schrödinger E. Diegegenwärtige situation in der quantenmechanik [J]. The Science of Nature, 1935,23(50):823-828.

[3] Schrödinger E. Discussion of probability relations between separated systems [J]. Proceedings of the Cambridge Philosophical Society, 1935,31(4):555-563.

[4] Feynman R P. Simulating physics with computers [J]. International Journal of Theoretical Physics, 1982,21(6/7):467-488.

[5] Shor P W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer [J]. Siam Review, 1997,26(5):1484-1509.

[6] Ekert A K. Quantum cryptography based on Bell’s theorem [J]. Physical Review Letters, 1991,67(6):661-663.

[7] 王合英，孙文博，陈宜保，等. 光子纠缠态的制备和测量实验[J]. 物理实验，2009，29(3)：1-5．

[8] 孙文博，王子逸，王合英，等. 分析自发分量下转换光场结构辅助搭建双光子纠缠源[J]. 物理实验，2014，34(4)：5-10.

[9] Koch K, Cheung E C, Moore G T, et al. Hot spots in parametric fluorescencewith a pump beam of finite cross section [J]. IEEE Journal of Quantum Electronics, 1995,31(5):769-781.

[10] Hsu F K, Lai C W. Absolute instrument spectral response measurements using angle-resolved parametric fluorescence [J]. Optics Express, 2013,21(15):18538-18552.

[11] 孙文博,王合英,陈宜保,等. Ⅰ类量子纠缠实验教学系统[J]. 物理实验，2016,36(6)：1-5.

[责任编辑：郭 伟]

Analyzing photon flux distribution of type-ⅡSPDC for adjustment of entangled twin-photon source

WANG Zi-yi1， WANG He-ying2, SUN Wen-bo2

(1. High School Affiliated to Renmin University of China, Bejing 100080， China;2. Department of Physics, Tsinghua University, Bejing 100084, China)

The photon flux distribution near the entangled photons in type-ⅡSPDC was investigated to help the adjustment of entangled twin-photon source. The result of this article further decreases the time needed for this teaching experiment and enhances students’ understanding for locating entangled photons. And the result provides basis for the precise mapping of type-Ⅱ SPDC and automatically adjusting program for entangled twin-photon source.

quantum entanglement; spontaneous parametric down conversion; photon flux; entangled twin-photon source

2016-05-30

国家基础科学人才培养基金支撑条件建设项目(No.J1210018)；清华大学实验室创新基金项目(No.110007019)

王子逸(1999-)，男，北京人，中国人民大学附属中学学生.

指导教师：孙文博(1980-)，男，辽宁锦州人，清华大学物理系工程师，学士，从事近代物理实验教学.

O431

A

1005-4642(2017)03-0052-04

“第9届全国高等学校物理实验教学研讨会”论文