一个条件不等式的推广及其应用

福建省莆田第三中学(351100) 翁国富

一个条件不等式的推广及其应用

福建省莆田第三中学(351100) 翁国富

我们知道,长方形的对角线与相邻两边所成的角α,β满足cos2α+cos2β=1且有tanαtanβ=1.由此容易得到

结论1 设锐角α,β满足 cos2α+cos2β=1,则tanαtanβ=1.

无独有偶,文[1]通过构造长方体,利用长方体的对角线与三条棱所成角α,β,γ和三条棱长的关系证得如下结论2所示的条件不等式：

结论2 设锐角α,β,γ满足cos2α+cos2β+cos2γ=1则tanαtanβ tanγ≥(易知当且仅当α=β=γ时等号成立).

结论1、2分别揭示了二维平面内的长方形、三维空间内的长方体的对角线与边(棱)所成角的内在联系,如果推广到n维空间,会有什么样的相应结论?即若锐角α1,α2,···,αn满足cos2α1+cos2α2+···+cos2αn=1,那么tanα1tanα2···tanαn≥?

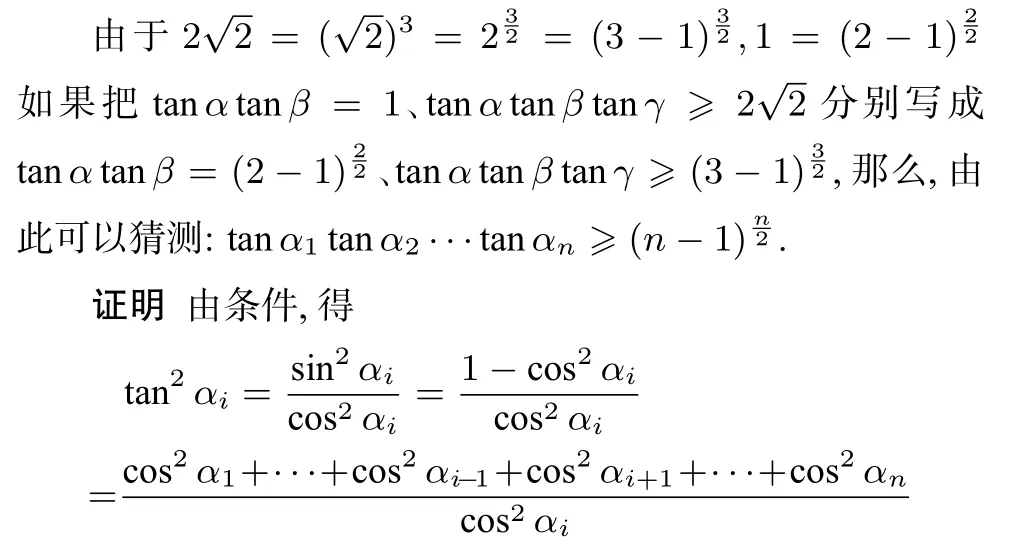
结论3若锐角α1,α2,···,αn满足cos2α1+cos2α2+ ···+cos2αn=1,则当且仅当n=2或α1=α2=···=αn时等号成立.

结论3揭示了n维空间内的“长方体”的“体对角线”与相邻的“棱”所成角的内在联系.特别地,当n=2,3、时,结论3分别为结论1、2.

以上结论有着广泛的应用,如果用于解决一类条件不等式问题,可以使问题化繁为简,化难为易,收到意想不到的效果.兹举例说明.

[1]程贤清.构造长方体巧证不等式[J].中学数学研究(华南教大), 2014,10.