例谈复合函数零点问题的求解策略

江苏省丹阳市教师发展中心(212300) 汪正文

例谈复合函数零点问题的求解策略

江苏省丹阳市教师发展中心(212300) 汪正文

问题的提出

复合函数的零点问题是高中数学的一个难点和热点,不仅涉及到函数的各种性质,蕴含着丰富的数学思想与方法,同时还由于其具有“内”“外”两层函数的特殊性,从而增添了解题所需的思维难度.对于这类问题,学生普遍感觉难以把握,本文试图从复合函数的定义、有关零点的命题以及典型题例的剖析着手,从中归纳出解题要领,以飨读者.

1 复合函数的定义

设函数u=φ(x)的定义域为是A,值域是B;又设函数y=f(u)的定义域是C,且B⊆C,y∈M,这时对A内每一个x,通过φ,得到B内唯一的一个u与此x对应,再通过f又得到M内唯一的一个y与此x对应.因此对于A内的每一个x先通过φ再通过f,得到M内唯一的一个y与此x对应,这就确定了一个从A到M的函数,称它是由u=φ(x)与y=f(u)合成的复合函数(也称嵌套函数),记为y=f[φ(x)].称u为中间变量,为了叙述方便起见,不妨将u=φ(x)称为内层函数,称y=f(u)为外层函数.

2 有关命题与结论

函数的零点问题不仅与函数、方程、不等式、导数等知识交汇融合,同时还涉及“函数与方程”、“化归与转化”、“数形结合”、“分类与讨论”等数学思想.以下引入上述思想的相关命题,以便为下面的分析与求解提供理论支撑.

命题1函数y=f(x)在x∈D上有n个零点⇔方程f(x)=0在x∈D上有n个解⇔方程组在 x∈D上有n组解⇔函数y=f(x)的图像与x轴在x∈D上有n个交点(其中n∈N).

命题2函数y=f[g(x)]在x∈D上有n个零点⇔方程在x∈D上有n个解⇔方程组中x在D上有n个解(其中n∈N).

命题3若方程f(x)=0有m(m∈N)个不同的实数根x1,x2,···,xm,且方程f(x)=xi(1≤i≤m,i∈N+)有ni(ni∈N+)个不同的实数根,则函数y=f[f(x)]的零点共有(n1+n2+···+nm)个.

证明因为xi是方程f(x)=0的根,所以f(xi)=0,设l1,l2,···,lni为方程f(x)=xi的不同的实数根,所以f(l1)=f(l2)=···=f(lni)=xi,所以l1,l2,···,lni也为方程f[f(x)]=0不同的实数根,即l1,l2,···,lni为y=f[f(x)]的零点.故函数y=f[f(x)]的零点共有(n1+n2+···+nm)个.

命题4若方程f(x)=0有m(m∈N)个不同的实数根x1,x2,···,xm,且方程g(x)=xi(1≤i≤m,i∈N+)有ni(ni∈N+)个不同的实数根,则函数y=f[g(x)]的零点共有(n1+n2+···+nm)个.

证明因为xi是方程f(x)=0的根,所以f(xi)=0,设l1,l2,···,lni为方程g(x)=xi的不同的实数根,所以g(l1)=g(l2)= ···=g(lni)=xi,所以l1,l2,···,lni也为方程f[g(x)]=0不同的实数根,即l1,l2,···,lni为y=f[g(x)]的零点.故函数y=f[g(x)]的零点共有(n1+n2+···+nm)个.

上述命题充分体现了四大数学思想,通过分类讨论和数形转换,不仅为图像法在解决函数零点问题中的运用提供理论保障,同时还为处理嵌套函数零点问题提供了求解方向,即研究内外层函数零点的情况.

3 典例解析

3.1求零点个数问题

例1设函数则函数y=f[f(x)]-1的零点的个数为___.

解析令f(x)=t,则问题转化为求方程组

图1

评注这是一道形如y=f[f(x)]+1型的嵌套函数,c为常数,通过换元解套后,将复合函数零点问题转化为两个简单方程解的个数问题,先由方程②解出t的值或范围,再代入方程①,数形结合即可求解.

例2已知函数f(x)=x3-3x,设h(x)=f(f(x))-c,其中c∈[-2,2],则函数y=h(x)的零点个数为___.

解析由f′(x)=3x2-3,则在(-∞,-1)上,f′(x)＞0,f(x)单调递增;在(-1,1)上,f′(x)＜0,f(x)单调递减;在(1,+∞)上, f′(x)＞0,f(x)单调递增,则其图像如图2所示.令f(x)=t,则方程,由图2知：

图2

当c=2时,由方程②解得：t1=-1,t2=2,

当t1=-1时,方程①为f(x)=-1,此时函数y=f(x)的图像与直线y=-1有3个交点;

当t1=2时,方程①为f(x)=2,此时函数y=f(x)的图像与直线y=2有2个交点,故当c=2时,函数y=h(x)共有5个零点;

同理,当c=-2时,函数y=h(x)有5个零点;

当0＜c＜2时,由图2知,方程②有3个根t3,t4,t5,且t3∈(-2,-1),t4∈(-1,0),t5∈(1,2).结合图2知,函数y=f(x)的图像与直线y=t3,y=t4和y=t5各有3个交点,故此时函数y=h(x)共有9个零点;

同理,当-2＜c≤0时,函数y=h(x)有9个零点.综上,函数y=h(x)的零点为5个或9个.

评注本题是2012年江苏卷最后一题的最后一问,属于y=f[f(x)]+c型的嵌套函数零点问题,但c为参数,通过换元解套后,将复合函数零点问题转化为两个简单方程解的个数问题.结合图2,先通过对c的讨论,研究方程②中t的个数及范围,再将t回代到①式,数形结合可得x的个数.

例3 已知函数 f(x)= x3-3x2+1,g(x)=,则方程g(f(x))-a=0(a为正实数)的实根最多有____个.

评注这是一道形如y=f[g(x)]+a型的嵌套函数,且a为参数,需要作出内外层函数的图像,先结合图4,对a予以讨论得到方程②中t的个数及范围,再结合图3,整合可求得方程①中的个数.

例4已知函数f(x)=x3+ax2+bx+c有两个极值点 x1,x2,若f(x1)=x1＜x2,则关于x的方程3[f(x)]2+2af(x)+b=0的不同实根个数为____.

解析令f(x)=t,则原方程

由f′(x)=3x2+2ax+b,画出y=f(x)的草图5,又x1,x2是函数f(x)的两极值点,则x1,x2是方程②的两实根,又f(x1)= x1＜x2,由图5知：当t=x1时,方程①有2解;当t=x2时,方程①有1解,故原方程共有3个实根.

图5

评注本题是2013年安徽卷第10题,解决本题的关键有两点：(1)关注到方程3[f(x)]2+2af(x)+b=0就是把f(x)代入导方程f′(x)=0而得;(2)换元解套,将一个看似复杂的函数零点问题拆解为两个简单的方程解的问题,当然问题的解决始终离不开“数形结合”.

3.2已知零点个数求参数范围问题

例5 若函数 f(x)=方程f[f(x)]=a只有五个不同的实根,则实数a的取值范围___.

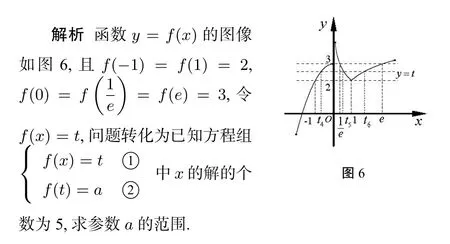
评注本题涉及两个层次的讨论,一是结合图形对a作4种分类,二是由于是分段函数,在同一大层次下,要根据函数变量x范围的限定,相应对t进行讨论,进而整合求解.

例6 已知函数f(x)=若函数y=f[f(x)-a]有4个零点,则实数a的所有可能取值构成的集合是___.

评注利用数形结合时,准确作图至关重要,由于所作图像是局部的,其关键点、关健线及变化趋势若关注不够,极易导致错误结果.本题若未注意到是x＜0时f(x)的一条渐进线,就会列出-1＜a-1＜0且或且的错误式子.

例7设定义域为R的函数

若函数g(x)=f2(x)-(2m+1)·f(x)+m2有6个零点,则实数m的范围为___.

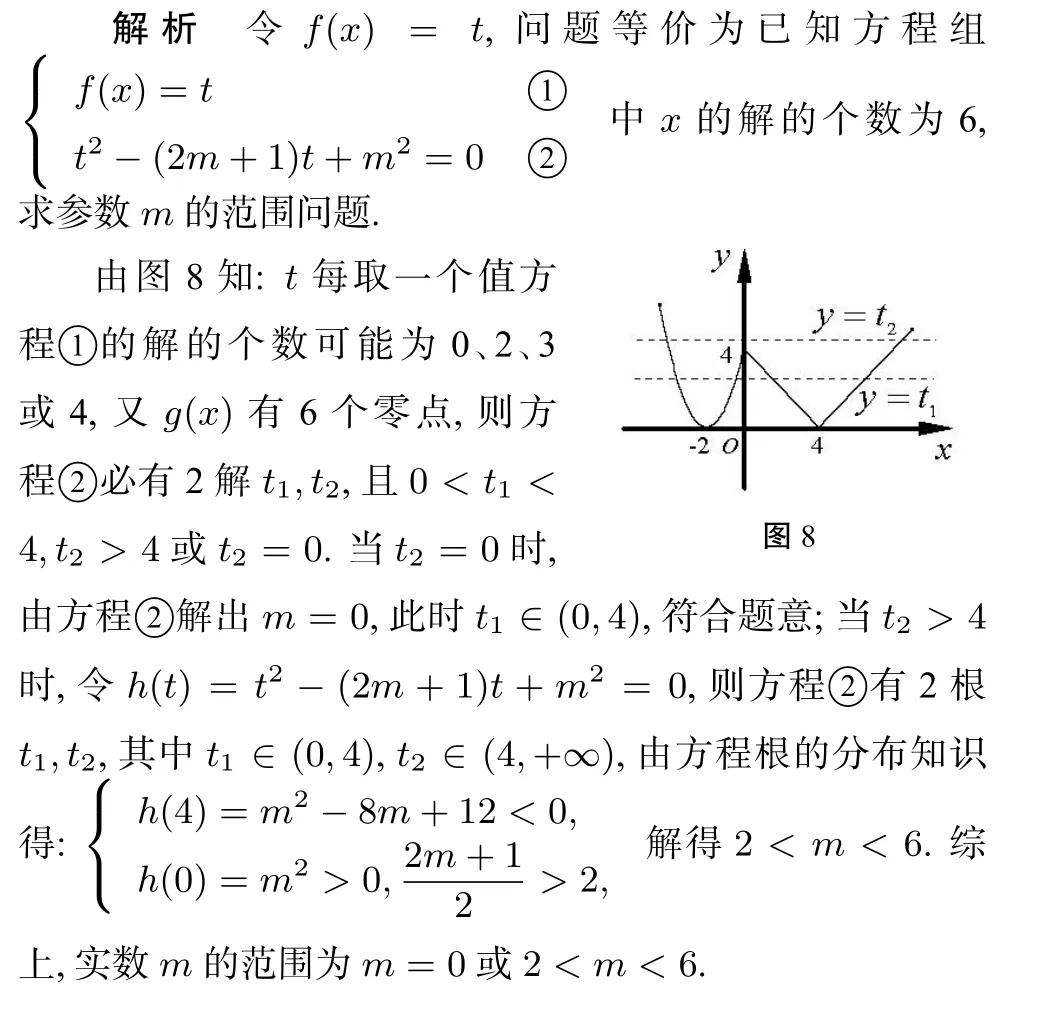
评注本题是形如y=af(x)2+bf(x)+c型嵌套函数,整合考虑内层函数f(x)的图像特征及零点情况,从而将问题转化为一元二次方程有两根解t1,t2,其中0＜t1＜4且t2=0或0＜t1＜4且t2＞4的分布情况,进而由根的分布知识予以求解.嵌套函数的零点或方程根的问题,常与函数的单调性、奇偶性、周期性、对称性等融合在一起,蕴含着函数与方程、数形结合、分类讨论等数学思想与方法.

一般地,对于形如y=f[g(x)]+a型函数零点问题的求解方法,通常是采用数形结合法,先作出内外层函数图像,把函数的零点或方程根的问题转化为函数图像与直线y=k的交点问题;其具体路径：(1)换元解套,令g(x)=t,从而将嵌套函数问题拆解为两个简单的内外层函数t=g(x)和y=f(t);(2)分别画出内外层函数的图像;(3)数形结合,先由f(t)=a,得到t的个数或范围,再将t代入g(x)=t得到x的个数或范围,而对于含参嵌套函数,在上述解题策略的基础上,让含参的值动起来,结合图像特征合理分类,整合予以求解.

[1]杨卫.复合函数的零根探究[J].数学学习与研究,2015(15)：120-121.

[2]宋村,邹生书.复合函数有关零点问题的解法[J].中学数学研究, 2013(10)：39-41.

[3]林慧明,罗明霞.运用换元法巧解一类复合函数零点问题[J].高中数学教与学,2014(6)：7-9.