透视几何概型应用中的易错点

广西壮族自治区柳江中学(545100) 杨艺

透视几何概型应用中的易错点

广西壮族自治区柳江中学(545100) 杨艺

“几何概型”是新课程新增加的内容之一,数学课程标准将其定义为：信息化的现代社会,统计和概率的基础知识已经成为一个未来公民的必备常识,要求学生“初步体会几何概型的意义,会进行简单的几何概率计算”.几何概型概念的理解,重在对试验的正确建模和几何度量的选择.在运用概念解题时,我们应注意不同的说法既可能是概念多样性的不同表述,但也可能导致对概念的本质理解产生偏差,也影响对几何度量的选择.因此,区别古典概型和几何概型,透视几何概型应用中的易错点有利于学生正确理解和掌握几何概型.

一、几何概型的定义与特点

(一)几何概型的定义如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型,简称几何概型.

(二)几何概型的特点(1)无限性,即一次试验中,所有可能出现的结果(基本事件)有无限多个;(2)等可能性,即每个基本事件发生的可能性均相等.

(三)几何概型的计算公式在几何概型中,事件A的概率的计算公式如下：

说明(1)事件A可以理解为试验的全部结果所构成的区域Ω的某一子区域,事件A的概率只与区域A的度量(长度、面积或体积)成正比,而与A的位置和形状无关.(2)用几何概率公式计算概率时,关键是构造出随机事件所对应的几何图形,并对几何图形进行度量.

二、古典概型和几何概型的联系和区别

(一)古典概型和几何概型的联系每个基本事件发生的都是等可能的.

(二)古典概型和几何概型的区别(1)古典概型的基本事件是有限的,几何概型的基本事件是无限的;(2)两种概型的概率计算公式的含义不同.

三、几何概型的应用中的易错点

(一)对几何概型中试验区域的理解误区

例1(2009山东卷•文理)在区间[-1,1]上随机取一个数x,的值介于0到之间的概率为( ).

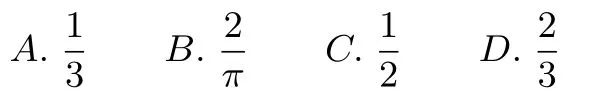
点评根据几何概型的定义,在区间上随机取任何一个数都是一个基本事件.所取的数是区间的任意一个数,基本事件是无限多个,而且每一个基本事件的发生都是等可能的,因此事件的发生的概率只与自变量的取值范围的区间长度有关,符合几何概型的条件.例1中构成事件区域的元素是自变量x的取值范围,而不是的取值范围,所以解法二是正确的,解法一是错误的.

例2.若实数a,b满足a2+b2≤1,则关于x的方程有实数根的概率是( )

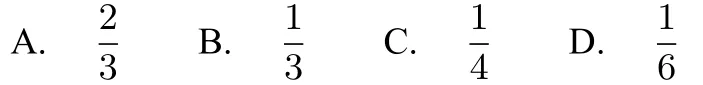
解法一关于x的方程有实数根等价于Δ≥0,即a2-3b2≥0.从而对应区域分别如图1和2所示,面积分别为所以所求概率为

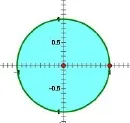
图1

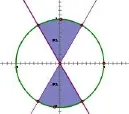
图2

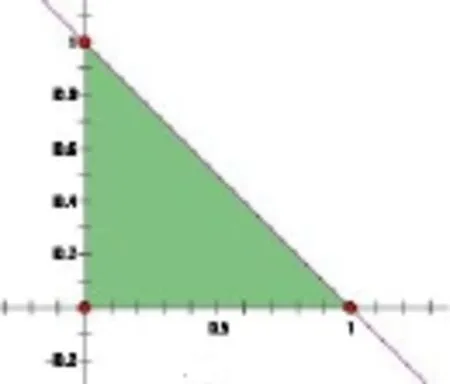
图3

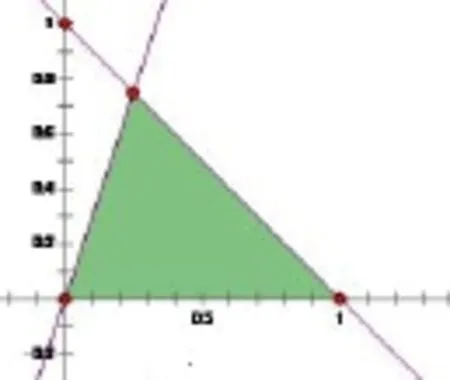
图4

点评例2中构成事件区域的元素是数对(a,b),而不是(a2,b2),所以解法一是正确的,解法二是错误的.

小结导致这两个题目错解的共同原因是都是因为通过变换改变了原来区域的大小,而且在改变过程中前后区域大小的比例不同.比如题1中自变量原来的取值区间[-1,1],经过余弦变换后得到的区间是[0,1],变换前后区间长度的比值为2;的取值区间经过逆变换得到区间长度为变换后前的长度比值为题2中图1和图3面积之比为2π,图2和图4之比为π.

(二)对几何概型中几何度量的理解误区

例3 在0～1之间随机选择两个数,这两个数对应的点把0～1之间的线段分成了三条线段,试求这三条线段能构成三角形的概率.

在平面上建立如图所示的直角坐标系,直线x=0,x= 1,y=0,y=-x+1围成如图所示三角形区域G,每一对(x,y)对应着G内的点(x,y),由题意知,每个试验结果出现的可能性相等,因此,试验属于几何概型,三条线段能构成三角形,当且仅当

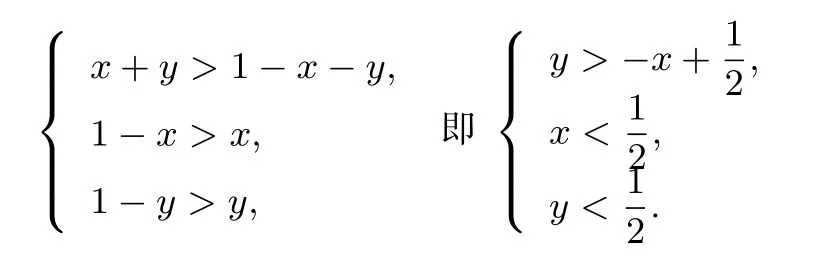
因此图5中的阴影区域D就表示“三条线段能构成三角形”,容易求得D的面积为G的面积为则P(这三条线段能构成三角形)=

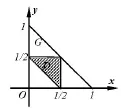
图5

图6

点评本题误把长度看作几何度量.

例4如图6所示,在等腰直角△ABC中,过直角顶点C在∠ACB内部做一条射线CM,与线段AB交于点M,求AM＜AC的概率.

分析当AM=AC时,有∠ACM=∠AMC,故欲使AM＜AC,应有∠ACM＜∠AMC,即所作的射线应落在∠ACM=∠AMC时∠ACM的内部.

点评本题所求事件的本质是在∠ACB内部做一条射线CM,所构成的区域是一个“角”域,故应属于几何概型中的角度之比类型;本题极易易犯的错误是,用长度的比得出这一错误结果.

小结此类题易把构成事件的区域看作长度,关键是要搞清每一结果是在什么区域内产生的.例3的几何度量为面积,而不是长度.例4根据在∠ACB内部作一条射线CM可知,射线构成的区域是一个角域,而不是一条线段.

[1]孙福明.“几何概型”教学必须关注的三个问题[J].高中数学教与学,2012,2.

[2]吴锷.自然流畅水到渠成—“几何概型”课堂观察与点评[J].高中数学教与学,2012,4.