函数思想在不等式比较大小与方程有解问题中的应用

广东广雅中学(510160) 赖淑明

函数思想在不等式比较大小与方程有解问题中的应用

广东广雅中学(510160) 赖淑明

比较指数、对数式的大小,讨论含指数、对数式的方程的根的问题,是高中代数的重要内容,这两类问题的解决方法有很多,但根源还是函数思想.本文借助五个命题,探索函数思想在比较不等式大小与方程有解问题解决中的应用.

性质1函数g(x)=xx(x＞0)在上单调递减,在上单调递增.

性质2 函数g(x)=在(0,e)上单调递增,在 (e,+∞)上单调递减.

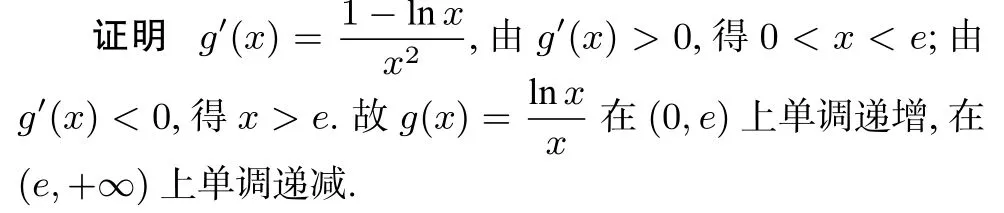
性质2推论当0＜a＜b＜e时,ab＜ba;e＜a＜b时,ab＞ba.

性质3 f(x)=logx(x+t)(t为常数,t＞0)在(1,+∞)上单调递减.

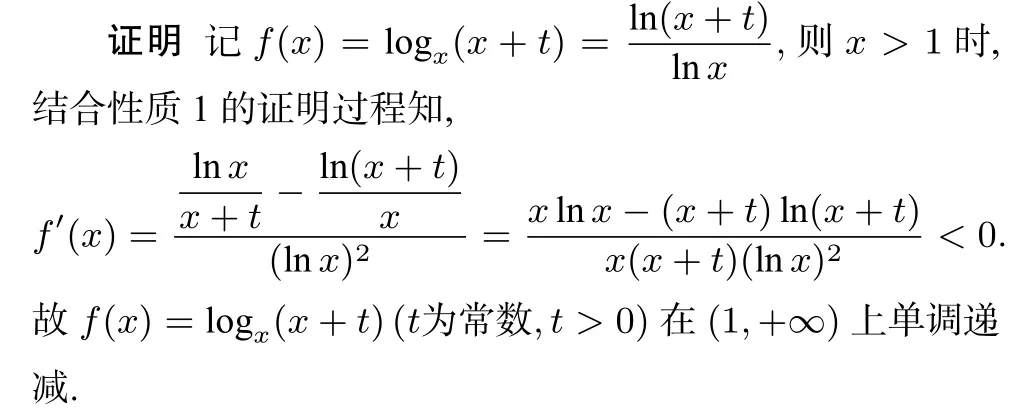
例1比较0.70.6,0.60.7,0.70.7,0.60.6,log67,log45六个数的大小关系.

解因为＜0.6＜0.7,所以根据性质1知0.60.6＜0.70.7.因为0＜0.6＜0.7＜e,所以根据性质2推论知0.60.7＜0.70.6.根据指数函数y=0.6x,y=0.7x的单调性知1＞ 0.70.6＞ 0.70.7、1＞ 0.60.6＞ 0.60.7.综上知0.60.7＜0.60.6＜0.70.7＜0.70.6＜1.因为1＜4＜6,所以由性质3可得：1＜log67＜log45综上所述可得：0.60.7＜0.60.6＜0.70.7＜0.70.6＜1＜log67＜log45.

例2(2014高考湖北理科卷)π表示圆周率,e= 2.71828···为自然对数的底数．

(2)求e3,3e,eπ,πe,3π,π3中的最大数与最小数;

(3)将e3,3e,eπ,πe,3π,π3这6个数按从小到大的顺序排列,并证明你的性质．

综上所述,比较两个数的大小,最终可以转化为函数单调性问题.解决问题的基本思想就是函数思想,通过构造函数,借助函数的单调性比较两个数的大小.

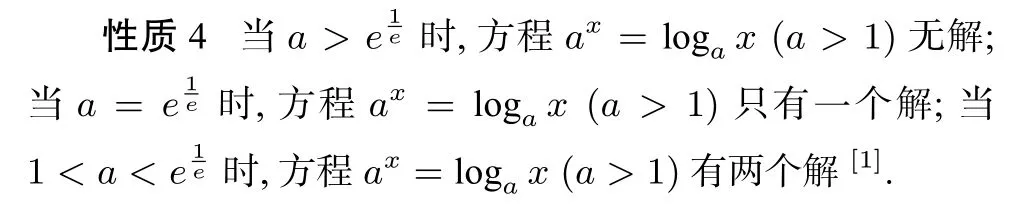
性质5当e-e≤a＜1时,方程ax=logax(0＜a＜1)只有1个解;当0＜a＜e-e时,方程ax=logax(0＜a＜1)有3个解[1].

例3判断下列方程的解的个数.

解因为所以根据性质4知,方程的解的个数是0.因为0＜0.06＜e-e,根据性质5知方程(0.06)x=log0.06x的解的个数是3.

综合以上分析,性质4适用于判断型如ax=logax(a＞1)的方程的解的个数,性质5适用于判断型如ax= logax(0＜a＜1)的方程的解的个数.

求解方程的根的问题,也是求解函数零点的问题.讨论超越方程根的个数问题,更多地可以转化为利用函数性质,研究函数零点个数的问题.

由此可见,抓住函数本质,许多数学解题中的难点问题可以有效突破.

[1]宗敏.对数函数与指数函数图象的交点个数的再探讨[J].考试周刊.2010.3