谈一个数列极限的求法

关键词：数列极限；定积分定义；瑕积分

若选用了高等教育出版社出版的《数学分析》第三版（上册）作为教材的人可能会发现该书第66页处有这样一道习题：

第24题（4）小题：

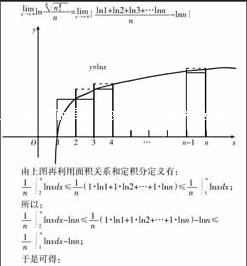
与式（1）的形式进行对比，就会发现，我们只需将式（1）中的数列求倒数后取其对数后可得到（2）式。于是可直接引用（1）式结论（式（1）的证明较易，在这里不再赘述）有：

但是，我们很快会发现被积函数在Inx在[0，1]上的O点不连续，甚至无界。我们通常在利用定积分定义来求数列极限时要求被积函数应在所考虑的闭区间上连续。于时，我们为了避免以上情况的出现，可考虑采用夹逼法来求解极限。

再将（2）式变形为：

以上解法的确绕过了Inx在0处的障碍，使问题得到了完整的解决。但我们回过头来对式（3）进行观察即会发现为一瑕积分，且在区间上收敛。试想一下，我们能否通过瑕积分使问题得到解决？

在《数学分析讲义》第三版中对在区间（a，b]上，以a为瑕点的瑕积分给了如下定义：

由以上定义可以看出该定义及求值奠基于定积分基础之上，若将两定义结合可得到关于瑕积分原始的定义如下。

定义：设f（x）在区间（a，b]上以a为瑕点，取0<？浊

以上建立于补充定义基础上的解题过程，反映了解决這一类极限问题的一般方法。而对于其他极限问题，特别是当作成的瑕积分发散的情况，又需要另作讨论。

参考文献：

[1]刘玉琏，傅沛仁.数学分析讲义（上册）[M].高等教育出版社，1997.

[2]孙家永.解题方法与技巧.高等数学研究，2001.

作者简介：李永安，男，1981年1月出生，大学本科，就职于四川省雅安中学，研究方向为中学数学教育。

？誗编辑 鲁翠红