课堂教学中如何逐步培养学生学习数学的兴趣
2017-03-29赵惠珍
赵惠珍

“兴趣是最好的老师。”这就是说一个人一旦对某事物有了浓厚的兴趣,就会主动去求知、去探索、去实践,并在求知、探索、实践中产生愉快的情绪和体验,所以古今中外的教育家无不重视兴趣在智力开发中的作用。
进入初中后,数学上引进了负数和字母代替数,这是数学知识的飞跃,对学生来说,学数学成了头疼事,有些家长说,小学都能考好,中学怎么了?学校提倡教师苦教,学生苦学,苦学是最好的方法吗?孔夫子说:“知之者不如好之者,好之者不如乐之者。”这就说明要乐学,而要达到乐学,首先要好学,要有兴趣,作为一名数学老师,怎样培养学生学数学的兴趣呢?我是从以下几个方面做的。
一、注重发现数学自身的美,从而培养学生学习数学的兴趣
比如,我讲三角形的四心、外心、内心、垂心、重心时,在初一学习三角形的高线、中线、角平分线时,让每一个学生动手画任意三角形的高线、中线、角平分线,然后观察:无论三角形的形状如何,大小如何,也不管这个三角形是谁画的,三角形是画在什么地方,三角形的三条高总是交于一点(垂心),三条中线交于一点(重心),三条角平分线也交于一点(内心),我们在那么多动的图形中找到静止的东西。然后让学生再量一量,重心把每一条中线是否都分成了2比1,内心到每条边的距离是否相等,对于度量的结论学生肯定不会信服,我告诉学生,随着知识的增加,我们可以逐步去证明这些性质。内心到各边的距离相等,在初二学生学习了角平分线到角两边的距离相等后再让学生去证明,外心和垂心要等线段垂直平分线和圆的内容学习后才能和学生探讨,当时只告诉学生垂心和外心也有性质,等我们以后学到了再慢慢研究,但从本节课我们发现数学很美,学生也感到数学很奇妙。后来学习了线段垂直平分线后,我又让学生画出三角形三边的中垂线,然后观察得出;他们交于一点(三角形外心),又让学生动手量一量,外心到三角形各顶点的距离有什么特点,学生得出结论:距离相等。学习圆的时候,我让学生任画一个圆,再画这个圆的任意一个内接三角形,画出这个三角形的垂心,同时让学生去证明,三角形的垂心关于三角形各边的对称点都在它的外接圆上,重心的证明在平行四边形学完后可以证明,更简单的证法是学完相似后,用相似三角形的性质去证明。
二、用数学知识解决实际生活中的问题,激发学生的学习兴趣
学生在学习了三角形全等的知识后,让学生利用全等三角形的对应边相等,去设计不同的方案,测量池塘的宽,当学生找出不同的方法后,再告诉学生测量池塘的宽还可以用相似,这样学生就会眼睛发光,心想他想了那么多办法,只是其中的一种思想,还有其他思想,他们肯定期待学完相似后能用的方法。同时,我在其他资料上又找到下面材料,让学生去学习。
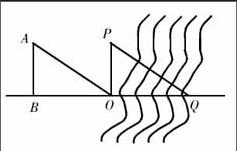
1805年,法军在拿破仑的率领下与德军在莱茵河畔激战,德军在莱茵河北岸Q处,如下图所示,因不知河宽,法军大炮很难瞄准敌营。聪明的拿破仑站在南岸的点O处,调整好自己的帽子,使视线恰好擦着帽舌边缘看到对面德国军营Q处,然后他一步一步后退,一直退到自己的视线恰好落在他刚刚站立的点O处,让士兵丈量他所站立位置B与O点的距离,并下令按照这个距离炮轰德军。试问:法军能命中目标吗?请说明理由。用帽舌边缘视线法还可以怎样测量,也能测出河岸两边的距离吗?法军能命中目标。
理由:已知AB=PO,∠A=∠P,
又∵AB⊥BO,PO⊥BQ,
∴∠ABO=∠POQ=90°,
∵在△ABO和△POQ中,∠A=∠P AB=PO ∠ABO=∠POQ=90°
∴△ABO≌△POQ(ASA),∴BO=OQ
因此,按照BO的距离炮轰德军时,炮弹恰好落入德军Q处;如果拿破仑站在O处,只需转过身来仍可用帽舌边缘视线法测出河岸两边的距离。
三、用一些很有名的定理证明提高学生的兴趣
学习勾股定理时,在引入新课时,我提问古埃及人民在沒有三角板的情况下是怎么用一根绳子画出直角三角形的,然后让学生自学课本,让学生体会毕达哥拉斯怎么就长了一双那么聪明的眼睛,能够发现勾股定理,而两千多年前,各国、各阶层的人民都找到了勾股定理的不同证明方法。
在1876年一个周末的傍晚,在美国首都华盛顿的郊外,有一位中年人正在散步,欣赏黄昏的美景,他就是当时美国俄亥俄州共和党议员伽菲尔德。他走着走着,突然发现附近的一个小石凳上,有两个小孩正在聚精会神地谈论着什么,时而大声争论,时而小声探讨。由于好奇心驱使伽菲尔德循声向两个小孩走去,想搞清楚两个小孩到底在干什么。只见一个小男孩正俯着身子用树枝在地上画着一个直角三角形。于是伽菲尔德便问他们在干什么?只见那个小男孩头也不抬地说:“请问先生,如果直角三角形的两条直角边分别为3和4,那么斜边长为多少呢?”伽菲尔德答道:“是5呀。”小男孩又问道:“如果两条直角边分别为5和7,那么这个直角三角形的斜边长又是多少?”伽菲尔德不假思索地回答道:“那斜边的平方一定等于5的平方加上7的平方。”小男孩又说道:“先生,你能说出其中的道理吗?”伽菲尔德一时语塞,无法解释了,心里很不是滋味。
于是伽菲尔德不再散步,立即回家,潜心探讨小男孩给他留下的难题。他经过反复的思考与演算,终于弄清楚了其中的道理,并给出了简洁的证明方法。他是这样分析的,如下图所示:
1876年4月1日,伽菲尔德在《新英格兰教育日志》上发表了他对勾股定理的这一证法。
1881年,伽菲尔德就任美国第二十任总统,后来人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把这一证法称为“总统”证法。
四、用一些特殊的题目提高学生的兴趣
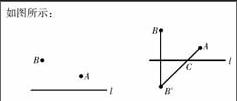
作点B关于直线l的对称点B′,连接AB′,与l的交点就是所要求作的点C。
理由:连接BC,∵点B与B′是关于直线l对称的,∴BC=B′C∴AC+BC=AC+B′C=AC
∴由A到C再到B的距离即为由A到C再到B′的距离,根据“两点之间,线段最短”,可知点C即为所求。
此题考查了轴对称——最短路径问题,将表达式转化为勾股定理,体现了数形结合在解题中的作用。
解1:如图1,作线段AB=2,过A作AC⊥AB,且AC=2,过B在AB的另一侧作BD⊥AB,且BD=1
在AB上任取一点P,设PA=a,则PB=b,则a+b=2,连结PC,PD,CD
构造如图2,其中AB=2,AC=2,BD=1,AC⊥AB,BD⊥AB
P是AB上任意一点,点C是点A关于直线AB的对称点
当D、P、E三点共线时,u的值最小,此时由勾股定理可求得
解3:由图3可知,最小值相对于点(0,2)和点(2,-1)的距离
还有很多激发学生兴趣的例子,比如说,在教学圆时可以可以向学生提问:为什么要把水管做成圆形?为什么把车轮要做成圆形?让学生通过实力去验证。处处留心皆学问,我们在平时教学工作和生活中多反思、多总结。
?誗编辑 鲁翠红
