重型桥式起重机桥架模态分析
2017-03-28宋晋民
宋晋民
(二重集团(德阳)重型装备股份有限公司,四川618013)
设 计
重型桥式起重机桥架模态分析
宋晋民
(二重集团(德阳)重型装备股份有限公司,四川618013)
本文通过对重型桥式起重机桥架进行四种工况下的模态分析,择其前4阶固有频率及其对应振型,对桥架结构的设计时,使其固有频率规避所受外激振的频率,这样可以避免产生共振效应,能有效减少振动幅值。
起重机;桥架;模态分析
随着国内起重机械行业蓬勃发展,有限元设计理念的推广和分析软件的普及应用,缩小了我国起重机设计与国外的差距。本文以2011年二重设计的江苏苏南重工550/100-34m A6 级桥式起重机偏轨箱形主梁为研究对象,运用有限元分析软件ANSYS Workbench,构建主梁的有限元力学模型,计算桥机系统的模态,探讨了桥机自振频率因受到参数的改变所引发的影响。
1 桥式起重机主要技术参数
桥式起重机主要技术参数有:起重量、起升高度、跨度(桥式起重机)、机构工作速度等[1],设计起重机要以此作为基本依据。
1.1 桥机桥架结构及载荷
桥机桥架结构及载荷情况如图1所示。
图1中各个参数的意义:
G1为大车运行机构的重量;
W为作用在主梁单位长度上的各均布重量叠加;
Gx为小车自重;
Q为额定起重量;
Fg为大车在运行时起、制动,满载小车移动产生的水平惯性力;
Wg为大车在运行时起、制动,由W产生的均布水平惯性力;
L为起重机跨度;
L1为大车运行机构重量;
G1为到大车车轮中性面的距离;
L2为司机室与电气设备总重量到大车车轮中性面的距离;
Lx为大车车轮轨距;
a为大横隔板间距;
B为桥架宽度;
B1为大车车轮轴距;
Bx为小车车轮轴距。
1.2 主梁结构
本文优化针对偏轨箱形主梁,其跨中主梁截面如图2所示。
图2中各参数的含义:
B1为上盖板宽度;B2为下盖板宽度;t1为上盖板厚度;t2为下盖板厚度;t3为腹板厚度;H为腹板高度;B为两腹板间隔距离。
本文中的桥架金属结构的主梁为偏轨箱形结构,内部布置成横向大、小隔板及纵向加劲板。对于偏轨双梁桥架,它的两根主梁与桥架中性面对称分布,载荷通过小车轮压作用在箱形梁的主腹板一侧,两根主梁的受力作用、形式是一样的,因此在载荷计算以及ANSYS分析中只需分析单根主梁即可[2]。
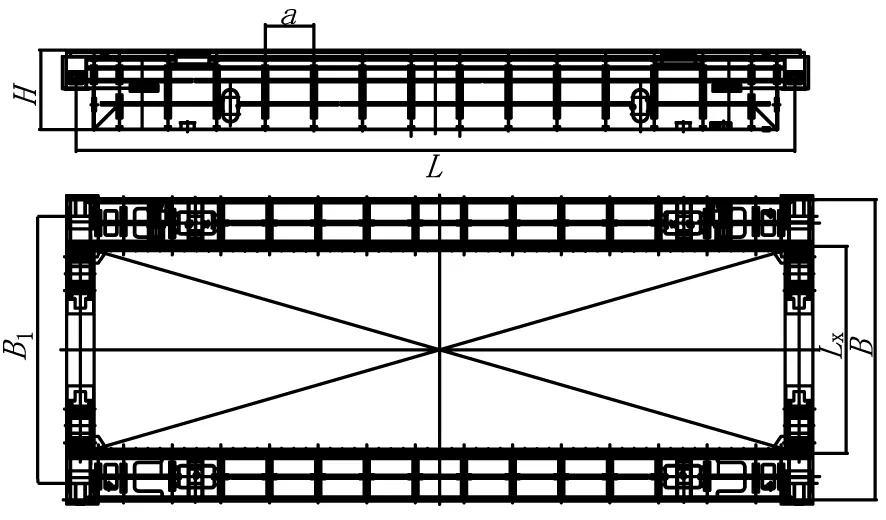
(a)桥架结构

(b)主要载荷

图2 主梁截面图
1.3 起重机主要技术参数
该起重机的主要技术参数和截面尺寸:
工作级别:A6
额定起重量:主550 t、 副100 t
大车轮距:B1=10 m
小车轮距:Bx=8.25 m
小车自重:Gx=2.97×105kg
小车起升高度:h=24.5 m
1.4 主梁参数
桥式起重机单根主梁外形如图3所示。
主梁参数为:
主梁自重:G主=1.16×105kg
主梁跨度:L=34 m
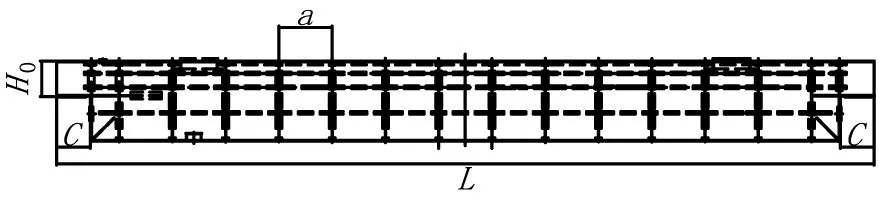
图3 主梁外形图

HB1/B2Bt1t2t3340024592181303018/20
主梁材料:Q345B
大隔板间距:a=2.3 m
变截面C=L/25,H0=L/25。
主梁截面参数值见表1。
2 桥架主梁载荷计算
2.1 载荷种类
在起重机械设计计算中,通常需要进行三类计算,分别是对起重机的零部件或机构的疲劳计算、强度计算和强度验算。所以计算载荷一般有三种组合[3]。
第Ⅰ类载荷组合,即正常工作时起重机所承受的正常载荷。
这种载荷组合用于计算零、部件和结构件的疲劳寿命、磨损或发热,它们都是等效载荷。在进行此类载荷计算时,通常仅需考虑正常情况下频发的载荷,如果在进行磨损和疲劳计算时,可不考虑风载荷施加的作用力。
第Ⅱ类载荷,即在恶劣环境下起重机工作产生的最大载荷,也称作强度计算载荷。
这类载荷用于抗倾覆稳定性验算和静承载能力计算,因为起重机械工作过程中可能会发生最不利的载荷组合,所以此种情况在核定该计算载荷时要加以考虑。最大载荷受限制的情况有:摩擦离合器;主动车轮打滑;电气保护装置动作;液压系统安全阀开启;安全销剪断;松闸装置作用(锻造起重机)等[1]。
第Ⅲ类载荷,验算载荷。
该类型载荷是在起重机工作时发生的事故载荷,或处于非工作状态时可能出现的最大载荷。产生这类载荷时,起重机一般不工作,即使进行工作的情况也极少[3]。
基于起重机实际工作状况,对其进行强度计算和载荷计算。计算主梁时忽略加强筋,简化为等截面梁。垂直方向上,当小车满载,运行至跨中位置时,会产生最大弯矩,所以选择跨中截面计算。
2.2 载荷分析
对主梁所承受的载荷进行简化,用简支梁的力学模型将单根主梁简化处理[1],如图4所示,重点考虑以下载荷:
(1)固定载荷:指主梁的自重,当对主梁加载时,只考虑主梁自重引起的固定载荷,在后面应用ANSYS Workbench分析时,设置重力加速度、主梁材料密度后,软件将自动计算出其自重[4]。

(a)主小车轮压分布图

(b)主梁受力分析图
(2)动载荷:即通过小车重量和额定起升重量产生,经过小车车轮传递到主梁上。在起升机构启、制动时,产生的惯性力,所以在确定作用在主梁上的小车轮压时,要考虑动载系数ψ2,根据《起重机设计手册》[4],选择ψ2=1.25,当小车运行至跨中时,小车轮压分别为P1和P2:

(1)
式中,P1为小车轮压1;P2为小车轮压2;L为跨度,L=34 m;l1为外侧车轮距支点的距离,l1=12.987 5 m;l2为内侧车轮距支点的距离,l2=14.112 5 m;b为内侧两车轮距离,b=5.775 m;E为钢材的弹性模量:E=2.1×1010kg/m2。
3 模态分析理论
模态就是结构本身所具有的振动特性,而模态振型、阻尼比和固有频率三个要素使每一个模态具体化[6]。通过计算和试验获得模态参数,这一获取过程称为模态分析。分析时,采用有限元计算方法取得模态参量称为计算模态分析;而采用试验方法取得模态参量称为试验模态分析。总之,模态分析是运用在动态设计、事故分析等方面的有效手段。
作为动力学基础的模态分析,能够计算模型固有模态的固有频率和固有振型。因此在已知结构的固有频率下,在设计与改进时,可以免于外部激振频率等同结构的固有频率。通过对模态振型的进一步分析,掌握了扭转、弯曲刚度在主梁的分布状况。
模态分析的核心内容就是弄清模态参数。依据Alembert D原理,将弹性体的动力学问题转化为相对简单的静力学问题,需要相应的惯性力的概念,动力学的通用运动方程为:

(2)
式中,[M]为质量矩阵;[C]为阻尼矩阵;[K]为刚度矩阵;[X]为位移向量;f(t)为作用力向量;t为时间。
对于模态分析,则f(t)=0,[C]一般忽略,为无阻尼线性自由振动系统。即M和K都是常量,没有阻尼,结构也没有激励。
无阻尼n自由度自由振动系统运动方程为:
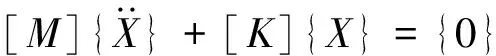
(3)
4 桥架系统模态分析步骤
在ANSYS Workbench软件的Mechanical模块下进行模态分析的过程,实际上和线性静态结构的分析过程相似,有八个步骤:
(1)建模。因为零位移约束是模态分析中唯一有效的载荷, 虽然在模态分析中可以指定载荷,但是在提取模态时,载荷会被忽略掉,因而只需要给有限元模型添加边界约束条件。
(2)设定材料属性。在ANSYS Workbench软件中,材料是在Engineering data里面设置的,默认为structural steel。
(3)存在接触,则定义接触对。
(4)进行网格划分。
(5)存在载荷,则要施加载荷。
(6)采用Frequency Finder设置要得到的结果。
(7)求解。
(8)查看结果。
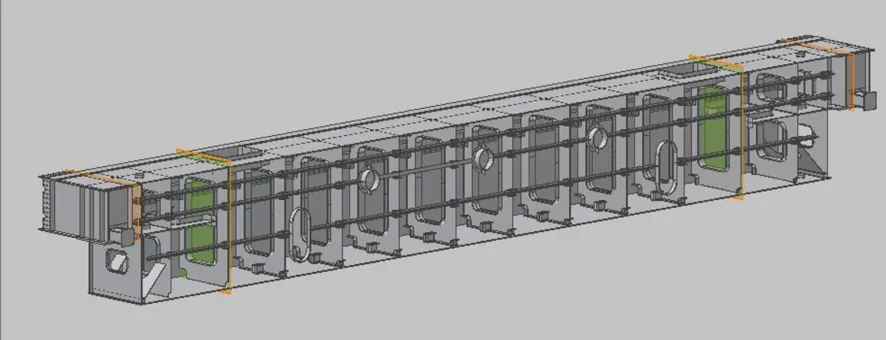
图5 桥架主梁三维模型
4.1 建模
通过应用Inventor对桥架主梁进行三维建模,如图5所示。
4.2 模型的简化
在进行有限元分析时,把所有复杂的情况都考虑进去是不可能的,也是不必要的,因为会使得模型非常复杂甚至不能计算,所以要根据有限元分析的适用条件对模型进行必要的简化。简化模型如图6所示。
(1)去掉模型中的纵向加劲板。由于主梁中纵向加强筋仅与提高主梁的局部稳定性有关,而主梁的强度、刚度都受其影响较小,所以建模时予以忽略,仅设置大隔板更接近实际[5]。
(2)忽略主梁端部和端梁结合处腹板厚度的变化,可把腹板看作是等厚度。

图6 简化的桥架三维模型图
桥架结构相关参数如前所述,可供选择的单元类型为三维壳单元SHELL181,此单元元素是由四个节点构成的四边形壳单元,无需定义截面和偏置。对大车左侧端梁支撑面处进行完全约束,而在大车右端梁两个支撑面处局部约束。桥架结构的力学模型如图7所示。
桥架的网格划分不是十分复杂,针对桥架结构模型,其不规则面通过自动划分方式,并采用自由网格划分,而其规则面则用映射划分。选取合适规格的单元,并将主梁与端梁的搭接接头做相应处置,为了确保计算结果较为精准,桥架结构几何模型被划分成规则的四边形状。求解结果的精度取决于网格划分的精度。通过网格划分,桥架几何模型的节点数共计28 992个,单元总数共计30 016个。如图8所示。
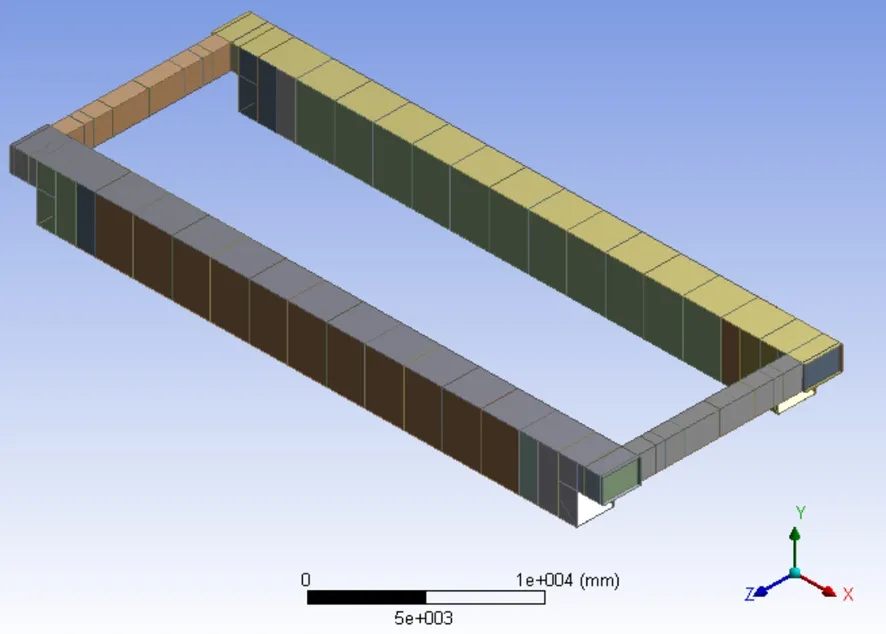
图7 在ANSYS Workbench DesignModeler中的桥架力学模型图
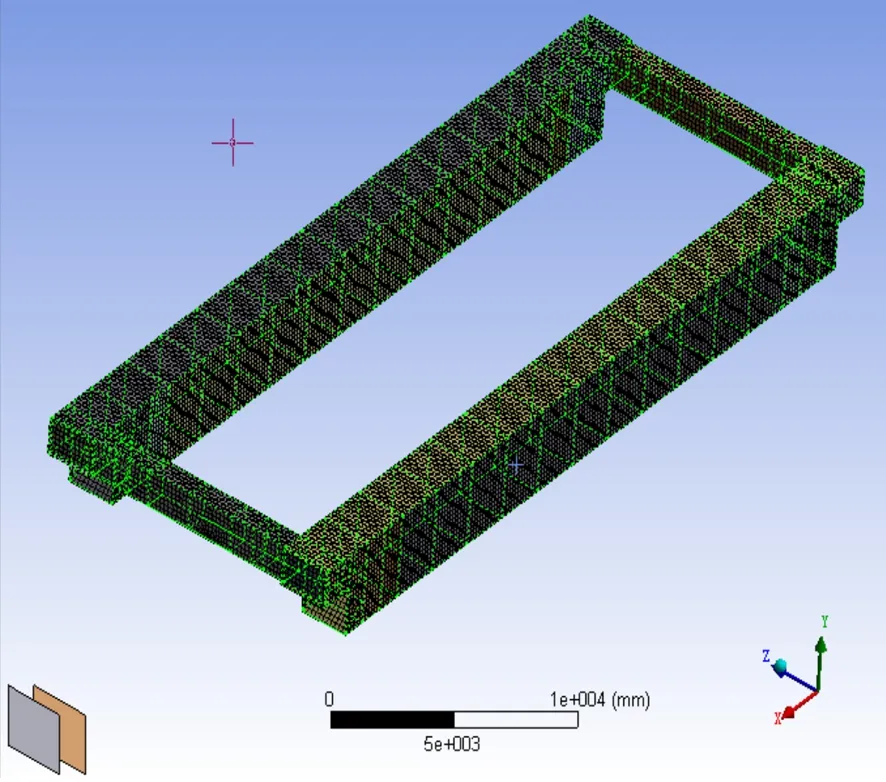
图8 模型在 ANSYS Workbench中网格化
4.3 桥架系统的模态计算
依据ANSYS Workbench软件进行模态分析的计算条件,仅仅考虑桥架的自重、零位移约束,忽略其余载荷[7],最后求出桥架前四阶固有频率见表2,振型见图9。
由图9和表2可以看出:
(1)通过数据分析,当外部激励频率和图表中数值接近时,振幅较大,桥架就会受损,所以,应通过设计降低振动和改变频率范围以避免出现整机振动。
(2)通过对图9中前4阶模态振型的研究得知,只有在外部频率接近主梁固有频率时,才发生共振现象,此种情形下振动较严重的部位是腹板,并形成危险区域,因此在考虑腹板时,一定不能忽略振动的影响因素。

表2 桥架前四阶固有频率

(a)一阶振型(b)二阶振型(c)三阶振型(d)四阶振型
图9 桥架前四阶振型图
Figure 9 The first four vibration mode diagram of bridge frame
(3) 按照GB/T 3811—2008,作为振动系统的动刚度,在满载时,钢丝绳卷筒放下的绳长度约等于额定起升高度时,系统用垂直平面的最低阶固有频率(简称满载自振频率)来表征。对于门式、桥式起重机和装卸桥,当小车运行在跨中时的满载自振频率f应不小于2 Hz[4]。从以上分析可知,起重机满足动刚度要求。
5 结论
为了认知桥架结构的动态特性,根据桥架结构的实际情况施加载荷和约束,并运用ANSYS Workbench软件进行模态分析,提取前几阶固有频率、振型图。通过分析主梁在承受主要载荷情况下的低阶模态,进一步对其低阶振型进行分析,得知当外界激励频率接近主梁自振频率时,主梁振动的主要表现形式为腹板的弯曲和扭曲,因此要想改变振动出现的频率范围,降低上述振动,就必须在设计时通过改变整机结构来获得。
[1] 张质文.起重机设计手册[M].北京:中国铁道出版社,1998.
[2] 程丽珠.桥式起重机主梁结构分析和优化设计[D].吉林:吉林大学,2006.
[3] 陈道南,盛汉中.起重机课程设计[M].北京:冶金工业出版社,1993.
[4] 起重机设计手册编写组.起重机设计手册[M].北京:机械工业出版社,1980.
[5] 皮智谋,宁朝阳.有限元分析软件ANSYS在箱形梁中的应用[J].机电产品开发与创新,2008,21(3):126-128.
[6] 吴琦. 支架设备结构模态实验及计算分析评价[D].大连:大连理工大学,2008.
[7] 曾春. 基于ANSYS的桥式起重机桥架结构有限元动态分析研究[D].武汉: 武汉理工大学,2006.
编辑 陈秀娟
Modal Analysis on Bridge Frame of Heavy Bridge Crane
Song Jinmin
Modal analysis has been carried out for four working conditions of bridge frame of heavy bridge crane, and the first four natural frequencies and the corresponding vibration modes have been chosen. When designing the bridge structure, it makes its natural frequency avoid the vibration frequency of external excitation, which can avoid the resonance effect, and effectively reduce the vibration amplitude.
crane; bridge frame; modal analysis
2016—09—18
TH215
A
