超声速和高超声速燃烧的数值研究

李恩义,乐贵高,马大为,张英琦,高 俣

(1.南京理工大学 机械工程学院,江苏 南京 210094;2.中国北方工业公司,北京 100053)

超声速和高超声速燃烧的数值研究

李恩义1,乐贵高1,马大为1,张英琦1,高 俣2

(1.南京理工大学 机械工程学院,江苏 南京 210094;2.中国北方工业公司,北京 100053)

为了研究HLLC黎曼求解器在超声速和高超声速燃烧问题中的适用性,对4个典型算例进行了数值模拟。基于多组分方程的完全N-S方程,对时间项和空间项离散分别采用2阶Runge-kutta方法和HLLC格式,考虑了H2/Air燃烧的详细化学反应机理,用有限速率化学反应模型模拟燃烧现象。对Sod激波管问题和高超声速钝体绕流进行数值模拟,分析了流场内密度、压力和激波位置;对超声速燃烧和高超声速钝体激波诱导燃烧进行数值模拟,分析了流场内组分特性。数值模拟结果与实验结果或相关文献的计算结果吻合良好,表明了HLLC黎曼求解器在模拟复杂化学非平衡流场中能够准确地分析复杂的物理现象且具有较广的应用范围。

黎曼求解器;化学反应模型;超声速燃烧;高超声速燃烧

在航空航天领域中,超声速和高超声速湍流燃烧有重要的工程意义。比如,对于超声速燃烧装置的研究,由于氢气反应速度快,符合燃烧装置体积小、燃料流速快的特点,所以其在超声速燃烧装置中有着广泛的应用。此外,在高超声速飞行器的气动特性研究中,考虑带有化学反应的非平衡流是极其必要的;为合理分析设计超燃冲压发动机,也须研究带有化学反应的内部燃烧。碳氢燃料的燃烧是一个非常复杂的化学反应,反应会产生自由基、原子和离子等中间产物,而且其化学反应过程与燃料的着火、燃烧的效率以及飞行器的推力相关。燃料与空气的有效混合及其在超声速和高超声速气流中的着火以及稳定燃烧是研究的热点和难点[1]。

根据求解的湍流涡尺度,具有高度非线性的湍流燃烧可以划分为三大类:雷诺平均统计模式[2]、湍流大涡模拟[3]和湍流直接数值模拟[4]。在湍流燃烧模型中,为了使基本方程得到封闭,需要模拟平均化学反应速率,可采用湍流燃烧关联矩模型[5]、概率密度函数反应速率模型[6-7]和火焰面建表模型[8]。在超声速或高超声速流动中,激波和燃烧波会造成流场中温度、压力、组分质量分数和反应源项等的巨大变化,这促使流场中出现了大梯度的空间锋面[9]。空间锋面的捕捉对数值计算的精度有着很高的要求,需要采用高分辨率的计算格式,常见的如TVD[10],NND[11],ENO和WENO[12],AUSM+[13],AUSMPW[14],AUSMPW+[15]等格式。

国内外学者对超声速和高超声速燃烧做了大量的研究。国内,王伟臣[16]考虑10种组分,使用有限速率化学反应模型对羽流后燃现象进行计算,分析了不同来流马赫数和不同飞行高度时后燃对羽流红外辐射强度变化的影响。韩省思[17]研究了超声速燃烧对流体可压缩性的影响,并对标准k-ε湍流模型的可压缩性进行修正,考虑H2/Air详细化学反应机理的计算结果表明,壁面和燃烧对湍流影响都很大。刘君[18]为了研究超燃流动中不同化学反应模型的影响,采用ENO差分格式,模拟了超声速H2/Air预混合气体中钝体激波诱导的振荡燃烧流场,通过3种反应机理的温度、压力与实验值的对比,得到了合理的化学反应模型。张涵信[19]采用NND格式和H2/Air燃烧模型,研究了球头激波诱导燃烧流动,并分析了流场中爆震波、激波以及激波和爆震之间的相互耦合。国外,Kim等[20]研究了不同长深比凹腔以及改进型-后缘倾角等工况下的多组分流场和燃烧流场。Viswanath等[21]通过数值计算研究了JP-8燃料的4种不同化学反应模型,对比了各模型之间的差异性。Jeong Y C等[22]采用有限速率化学反应模型对底部排气弹进行了数值计算,燃烧反应模型采用了详细的10组分25步燃烧反应模型。

本文针对超声速和高超声速燃烧流场,采用基于HLLC的黎曼求解器方法来求解流场特性;在计算中考虑了多组分燃烧,使用有限速率化学反应模型模拟燃烧现象,计算了4种典型算例,验证了文中所采用的方法应用于激波捕捉和分析燃烧流场特性的合理性,为进一步分析提供合理的数值方法。

1 计算方法

1.1 控制方程

本文采用考虑非平衡化学反应的多组分可压缩N-S方程作为控制方程,为了简化计算,仅研究二维流动,其物理域笛卡尔坐标系表达式如下:

(1)

(2)

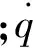
1.2 热力学特性

热力学特性取决于以下几个方程:

(3)

hi=(ai+biT+ciT2+diT3+eiT4)T+ΔHfi

(4)

(5)式中:cp,i为第i种组分的比定压热容,且它是系数分别为ai,bi,ci,di,ei的关于温度的四阶多项式;Gi为第i种组分的吉布斯自由能;ΔHfi为第i种组分在相应参考温度范围内的生成焓。

反应的吉布斯自由能由生成物与反应物的吉布斯自由能之差得到:

(6)

式中:ip表示生成物组分,ir表示反应物组分。

反应的平衡常数为

(7)

式中:Δν为生成物与反应物的物质的量之差,R0为通用气体常数,R1也是一个常数。

1.3 有限速率化学反应模型

有限速率化学反应模型是基于Arrhenius公式计算化学源项,则其化学反应方程式可写为

(8)

而反应中组分i的生成率为

(9)

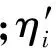
用Arrhenius公式表示的正向化学反应速率为

kf=ATbexp[-Ea/(RT)]

(10)式中:A为指前因子,b为温度T的指数,Ea为活化能。

在超声速和高超声速燃烧中,由于燃料在燃烧室内停留时间和化学反应时间尺度均非常小,因此会造成化学反应不完全和强烈的非平衡特性。为了准确地模拟燃烧流场的特性,必须考虑复杂的化学反应机理。针对H2/Air燃烧,本文采用了文献[23]的详细化学反应机理,反应包括了9种组分,18种基元反应,详细反应方程如表1所示,表中,ns为反应步数。

表1 H2和O2详细化学反应机理模型

*注:M代表第三体组分。

1.4 HLLC黎曼求解器

HLLC格式是基于HLL格式发展而来,它是一种Godunov类型格式。在该方法中,黎曼问题的解可以用图1所示的三波模型来进行近似,可写为

(11)

相应HLLC的数值通量FHLLC可以定义为

(12)

根据Rankine-Hugoniot条件,可得：

(13)

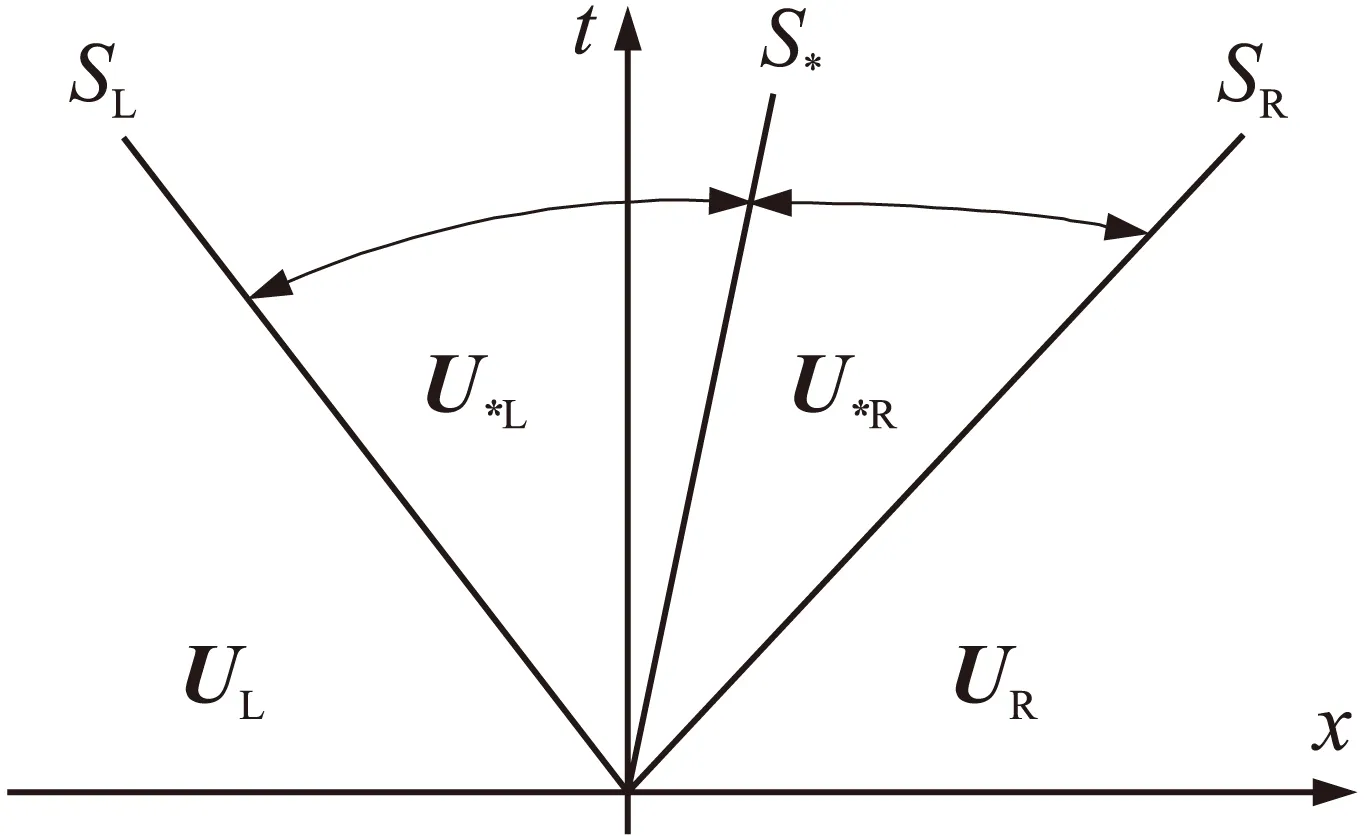
图1 HLLC黎曼求解器

对于式(11)、式(12)、式(13),3个方程却有4个未知通量,为了完成求解需要分析求解2个中间通量F*L,F*R,结合接触间断关系式,可以得出:

(14)式中:K代表R或L分别为激波右侧和左侧,S为波速,U为特征速度通量,“*”为中间通量,pLR为平均压力,详细分析说明可见文献[24]。同时,为了减小数值振荡,提高计算精度和稳定性,需引入Van Leer限制器:

(15)式中:r为当地平均函数的比值,详细说明见文献[25]。

1.5 时间离散

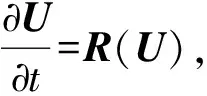
U0=Un

(16)

U(1)=U(0)+(Δt)R(U(0))

(17)

(18)

Un+1=U(2)

(19)

在数值计算中选取的CFL数为0.6。

2 计算结果与分析

2.1 Sod激波管问题

为了验证上述数值方法的激波捕捉精度,本文以典型的Sod激波管进行数值模拟,并与解析解进行对比。计算区域为[0,1]×[0,0.25],采用四边形结构网格,网格大小为Δx=Δy=1/200。图2、图3分别给出了在无量纲时间t*=0.2时刻,激波管中心轴线上的密度ρ与参考密度ρref之比的分布曲线和压力p与参考压力pref之比的分布曲线的数值解和精确解。

图2 沿x轴的密度分布图

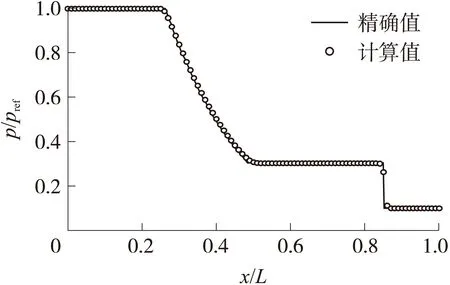
图3 沿x轴的压力分布图

从图2、图3中可以看出,数值解与精确解的吻合程度良好,表明该方法可以准确地捕捉到稀疏波、激波和接触间断。

2.2 高超声速钝体绕流

为了分析验证本文所采用的数值方法在高超声速流动中的激波捕捉能力,对文献[15]中的算例进行数值模拟。自由来流条件:来流速度u∞=3.63 km/s,来流温度T∞=293 K,来流压力p∞=2.4 kPa,钝体半径r0=0.007 m。计算网格采用四边形结构网格,壁面边界层Y+约为1,并对激波位置区域网格加密。图4给出了由HLLC方法计算得出的激波位置,可以看出该方法与实验值吻合良好。

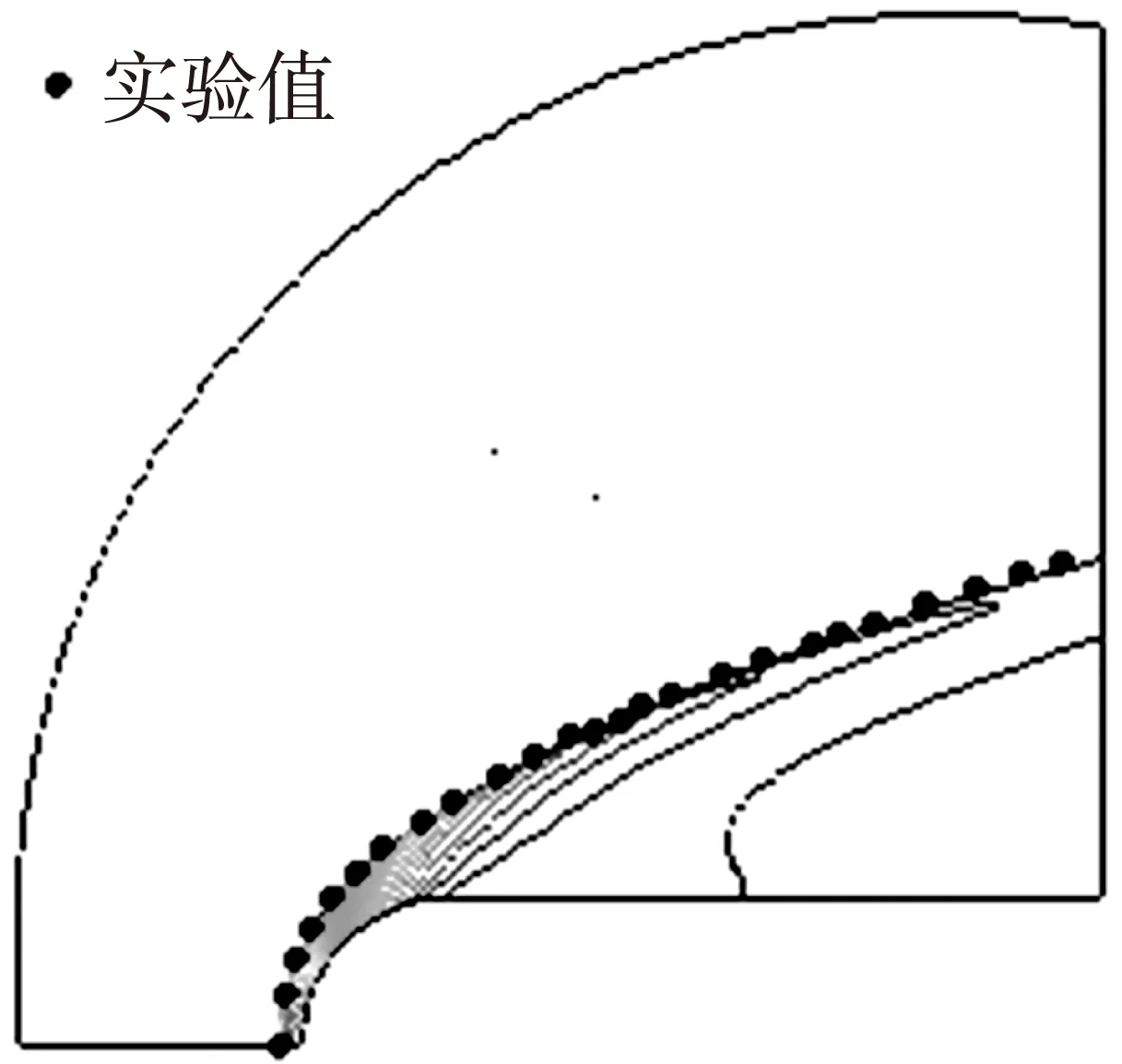
图4 计算压力等高线和实验激波位置图

2.3 超声速H2燃烧

本算例以Marshall和Kurkov[26]的H2/O2燃烧实验为研究对象。在流场计算中,考虑空气来流边界层,使其在x=0处边界层厚度约为1 cm。计算网格采用四边形结构网格,网格量为750×420,壁面边界层的Y+约为1,并在混合区加密网格。主流空气以及燃料氢气的进口边界条件参数见表2。实验装置示意、计算域和坐标轴的选取如图5所示。

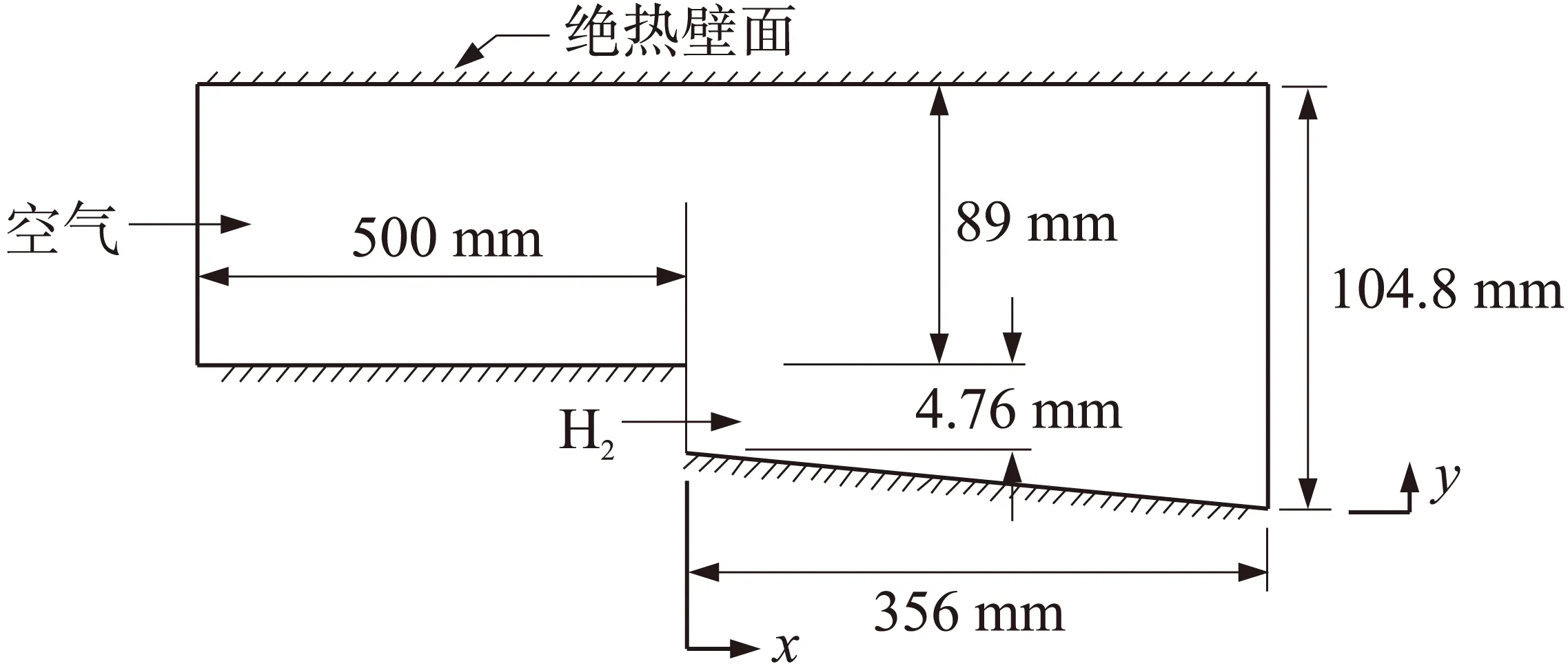
图5 实验装置的计算域

表2 H2和空气的进口边界条件

由于表2中所采用的是组分质量分数,为了与文献中体积分数保持一致,将质量分数w转化为体积分数φ,则第i项组分的体积分数φi为

(20)

式中:Mri为第i项组分的相对分子质量。

图6给出了在x=0.356 m处,出口边界上组分体积分数φ的模拟值和文献计算值对比图。从图中可以看出,文中所采用方法与文献值整体上吻合较好,仅在反应边界附近组分H2O的体积分数有些高估,说明了HLLC黎曼求解器在计算超声速燃烧问题上的有效性。

图6 x=0.356 m处4种组分体积分数的对比

2.4 高超声速钝体激波诱导燃烧

本算例通过数值计算模拟Lehr’s[27]的实验结果,选取的物理模型和自由来流条件:钝体半径r2=15 mm,来流马赫数Ma∞=6.46,来流压力p∞=42 732 Pa,来流温度T∞=292 K。

对于高超声速多组分钝体绕流,在弓形激波之后,由于黏性耗散效应和激波的强烈压缩,巨大的动能损失中的一部分转化为激波层内气体内能使激波后区域温度升高,引起混合气体燃烧。但由于流场中温度不够高,没有引起N2分子分解,不存在N原子及其相关的组分,故文中化学反应不考虑N2燃烧。H2/Air系统化学反应方程可写为:2H2+O2+3.76N2→2H2O+3.76N2。

由于N2的稀释作用下反应放热不足,驻点线上Von Neumann尖峰消失,爆震波与激波减弱。图7、图8和图9分别给出驻点线上的压力、密度和组分质量分数分布的计算值与文献[28]的对比,由图可见,各物理量吻合良好,可以说明HLLC黎曼求解器在计算高超声速燃烧问题上的有效性。

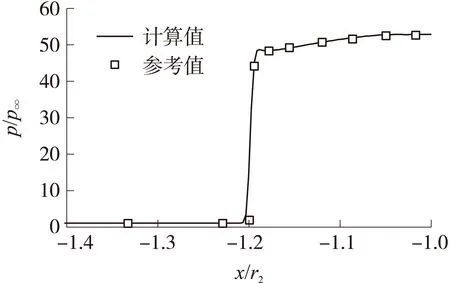
图7 驻点线上的压力对比

图8 驻点线上的密度对比

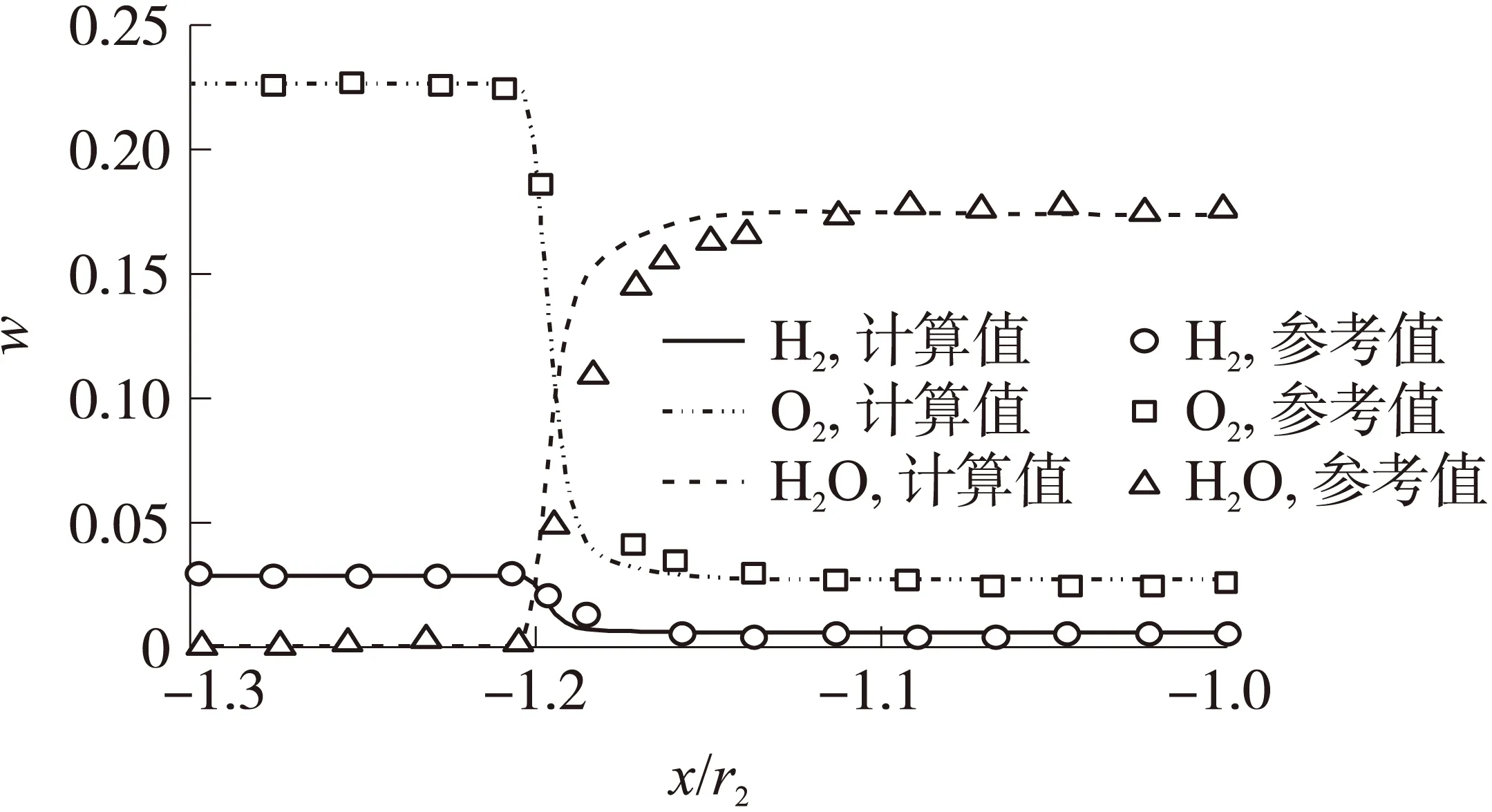
图9 驻点线上的主要组分质量分数分布对比

3 结论

本文基于HLLC黎曼求解器的通量计算格式,对Sod激波管问题和高超声速钝体绕流进行数值模拟,结果表明HLLC黎曼求解器在超声速和高超声速流场中激波捕捉方面具有良好的分辨率。此外,还计算了超声速和高超声速燃烧,数值计算结果与相关参考文献的实验值和计算结果吻合良好,说明了HLLC近似黎曼求解器在计算超声速和高超声速燃烧问题上的有效性,为下一步深入研究提供了依据。

[1] 司徒明.煤油超燃冲压发动机性能分析[J].推进技术,1998,19(2):19-23. SITU Ming.Preformance analysis of hydrocarbon-fueled scramjet[J].Journal of Propulsion Technology,1998,19(2):19-23.(in Chinese)

[2] 汪秋笑,黄东欣,孟华.甲烷-液氧超临界压力非预混湍流燃烧的数值模拟[J].航空学报,2016,31(7):2 132-2 143. WANG Qiu-xiao,HUANG Dong-xin,MENG Hua.Numerical simulation of CH4-LOx non-premixed turbulent combustion at supercritical pressures[J].Acta Aeronautica et Astronautica Sinica,2016,31(7):2 132-2 143.(in Chinese)

[3] 周力行.两相燃烧的大涡模拟[J].中国科学:技术科学,2014,44(1):41-49. ZHOU Li-xing.Large-eddy simulation of two-phase combustion[J].Scientia Sinica Technologica,2014,44(1):41-49.(in Chinese)

[4] 金台.超声速湍流燃烧多物理耦合的直接数值模拟研究[D].杭州:浙江大学,2015. JIN Tai.Supersonic turbulent combustion multi-physical coupled of direct numerical simulation studies[D].Hangzhou:Zhejiang University,2015.(in Chinese)

[5] KLIMENKO A Y,BILGER R W.Conditional moment closure for turbulent combustion[J].Progress in Energy and Combustion Science,1999,25(6):595-687.

[6] EIFLER P,KOLLMANN W.PDF prediction of supersonic hydrogen flames:AIAA 1993-0448[R].Reno,NV:AIAA,1993.

[7] BAURLE R A,GIRIMAJI S S.Assumed PDF turbulence-chemistry closure with temperature-composition correlations[J].Combustion and Flame,2003,134(1):131-148.

[8] PETERS N.Laminar flamelet concepts in turbulent combustion[C]//Symposium(International)on Combustion.Berlin:Elsevier,1988:1 231-1 250.

[9] 罗坤,金台,卢树强,等.超音速氢气燃烧火焰结构特性的直接数值模拟[J].工程热物理学报,2012,33(11):2 010-2 014. LUO Kun,JIN Tai,LU Shu-qiang,et al.DNS of flame structure characteristics in a supersonic hydrogen combustion[J].Journal of Engineering Thermophysics,2012,33(11):2 010-2 014.(in Chinese)

[10] HARTEN A.High resolution schemes for hyperbolic conservation laws[J].Journal of Computational Physics,1983,49(3):357-393.

[11] 张涵信.无波动、无自由参数的耗散差分格式[[J].空气动力学学报,1988,6(2):143-165. ZHANG Han-xin.Non-oscillatory and non-free-parameter dissipation difference scheme[J].Acta Aerodynamic Sincia,1988,6(2):143-165.(in Chinese)

[12] SHU C W.Essentially non-oscillatory and weighted essentially non-oscillatory schemes for hyperbolic conservation laws[M]//Advanced Numerical Approximation of Nonlinear Hyperbolic Equations.Berlin:Springer,1998:325-432.

[13] LIOU M S.A sequel to ausm:Ausm+[J].Journal of Computational Physics,1996,129(2):364-382.

[14] KIM K H,LEE J H,RHO O H.An improvement of AUSM schemes by introducing the pressure-based weight functions[J].Computers & Fluids,1998,27(3):311-346.

[15] KIM K H,KIM C,RHO O H.Accurate computations of hypersonic flows using AUSMPW+scheme and shock-aligned grid technique:AIAA 1998-2442[R].[S.l]:AIAA,1998.

[16] 王伟臣,魏志军,张峤,等.后燃对火箭发动机羽流红外特性的影响[J].航空动力学报,2010,25(11):2 612-2 618. WANG Wei-chen,WEI Zhi-jun,ZHANG Qiao,et al.Influence of afterburning on infrared signature of rocket motor exhaust plume[J].Journal of Aerospace Power,2010,25(11):2 612-2 618.(in Chinese)

[17] 韩省思,叶桃红,朱旻明,等.应用修正的k-ε模型研究超声速H2/Air燃烧[J].推进技术,2008,29(2):158-162. HAN Xing-si,YE Tao-hong,ZHU Min-ming,et al.Numerical simulation of supersonic H2/Air combustion appling modifiedk-εturbulence model[J].Journal of Propulsion Technology,2008,29(2):158-162.(in Chinese)

[18] 刘君.化学动力学模型对H2/Air超燃模拟的影响[J].推进技术,2003,22(1):67-70. LIU Jun.Numerical study on chemical mechanism in supersonic H2/ Air mixture gas flow[J].Journal of Propulsion Technology,2003,22(1):67-70.(in Chinese)

[19] 张涵信,陈坚强,高树椿.H2/O2燃烧的超声速非平衡流动的数值模拟[J].宇航学报,1994,4(2):14-23. ZHANG Han-xin,CHEN Jian-qiang,GAO Shu-chun.Numerical simulation of supersonic non-equilbrium flows for H2/O2combustions[J].Journal of Astronautics,1994,4(2):14-23.(in Chinese)

[20] KIM K M,BAEK S W,HAN C Y.Numerical study on supersonic combustion with cavity-based fuel injection[J].International Journal of Heat and Mass Transfer,2004,47(2):271-286.

[21] VISWANATH R K.Comparison of chemical-kinetics models for predicting premixed and non-premixed flames:AIAA 2006-4745[R].Sacramento,CA:AIAA,2006.

[22] CHOI J Y,SHIN E,KIM C K.Numerical study of base-bleed projectile with external combustion[C]//41st AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit.Ariiona:AIAA.2005:10-13.

[23] SHANG H M,CHEN Y S,LIAW P,et al.Investigation of chemical kinetics integration algorithms for reacting flows:AIAA 1995-0806[R].Reno,NV:AIAA,1995.

[24] TORO E F.Riemann solvers and numerical methods for fluid dynamics:a practical introduction[M].London:Springer Science & Business Media,2013.

[25] KEMM F.A comparative study of TVD-limiters:well-known limiters and an introduction of new ones[J].International Journal for Numerical Methods in Fluids,2011,67(4):404-440.

[26] BURROWS M C,KURKOV A P.An analytical and experimental study of supersonic combustion of hydrogen in vitiated air stream[J].AIAA Journal,1973,11(9):1 217-1 218.

[27] LEHR H F.Experiments on shock-induced combustion[J].Astronautica Acta,1972,17:589-597.

[28] YUNGSTER S,EBERHARDT S,BRUCKNER A P.Numerical simulation of hypervelocity projectiles in detonable gases[J].AIAA Journal,1991,29(2):187-199.

Numerical Investigation of Supersonic and Hypersonic Combustion

LI En-yi1,LE Gui-gao1,MA Da-wei1,ZHANG Ying-qi1,GAO Yu2

(1.School of Mechanical Engineering,Nanjing University of Science and Technology,Nanjing 210094,China; 2.China North Industries Corporation,Beijing 100053,China)

Four typical examples were numerically simulated to investigate the validity of HLLC Riemann solver in the application of supersonic and hypersonic combustion.Based on the perfect Navier-Stokes equations of multi-component equations,the convection fluxes was calculated by the HLLC scheme,while two-stage Runge-Kutta iterative method was used for time discretization.The detailed chemical reaction of H2/Air was considered,and the finite-rate chemical-reaction model was applied to simulate the combustion.Sod shock-tube problems and hypersonic flow around blunt body were numerically simulated,and the flow-field density,pressure and shock-wave position were analyzed.The supersonic combustion and the combustion induced by hypersonic-blunt-body shock-wave were simulated,and the composition characteristics of flow field was analyzed.The numerical simulation results are in good agreement with the experimental results or the related literature.By the HLLC Riemann solver,the complex physical phenomena can be accurately analyzed,and the solver has wide application range in complex chemical non-equilibrium flow-field.

Riemann solver;chemical reaction model;supersonic combustion;hypersonic combustion

2016-10-29

李恩义(1988- ),男,博士研究生,研究方向为计算流体力学。E-mail:lienyi_102@163.com。

TJ303.4

A

1004-499X(2017)01-0062-06