飞行器航迹测量数据的粗差探测模型优选方法
2017-03-28涂先勤谷德峰易东云周海银
涂先勤,谷德峰,易东云,周海银
(1.中国人民解放军91550部队,辽宁 大连 116023;2.国防科学技术大学 理学院 数学与系统科学系,湖南 长沙 410073)
飞行器航迹测量数据的粗差探测模型优选方法
涂先勤1,2,谷德峰2,易东云2,周海银2
(1.中国人民解放军91550部队,辽宁 大连 116023;2.国防科学技术大学 理学院 数学与系统科学系,湖南 长沙 410073)
为评估不同模型的粗差探测性能,使用多余观测数、内部可靠性和外部可靠性等指标对飞行器航迹测量数据处理中的3种典型模型的粗差探测能力进行了定量评估和比较分析。建立了不同模型间性能比较的等效规则,按照典型的工程应用场景进行了仿真实验。结果表明:大数据集模型的系统结构较强,具有更优的单粗差探测性能,但大模型对于多粗差探测是不利因素;在实际应用中,应根据粗差发生的统计特征,选取数据量大小合适、结构强度高的模型作为优选模型。
航迹测量;粗差;系统建模;优化模型
飞行器航迹测量数据的精密事后处理,需要依据某种准则对粗大误差进行识别,常用的有外推预报方法、多项式回归模型检验法、ARIMA检验法、M估计粗差剔除方法[1]、逐点剔除方法[2]。这些方法不一而足,哪个方法更优,难以定量分析评估。
上述这些方法中,有一类基于统计检验的粗差探测方法,经过抽象后可以建立高度理论化的表述,本文称之为粗差探测理论。粗差探测理论的主要贡献在于两点:①构造了粗差探测的理论最优检验;②建立了对模型的粗差探测能力进行定量化度量的概念体系,为定量比较不同模型的粗差探测能力提供了理论依据。
粗差探测理论揭示了对于同一组数据由于建模方法不同会导致粗差探测能力具有明显差异,模型优选是进行粗差探测建模中必须考虑的一个重要问题。本文以粗差探测理论为指导,对工程应用中常见的3种典型粗差探测模型的粗差探测能力进行了仿真分析和定量比较。先建立了不同模型之间定量比较的规则,然后基于典型应用场景利用仿真数据对3种不同模型进行比较分析,最后给出了粗差探测模型优化设计方法。
1 粗差探测模型理论描述
当数据中不含任何粗差时,标准模型为
Y=Xβ+ε
(1)

当数据中含有粗差时,含粗差模型为
Y=Xβ+δΔ+ε
(2)
式中:δ为m×p维的示性矩阵,其元素要么为0,要么为1,且每行每列只有唯一的元素等于1,1≤p≤m-n;Δ为p×1维待估计的粗差向量。
在模型(2)中,粗差向量Δ的最优估计为
(3)
(4)
此时,检验函数为
(5)
式中:α为检验的显著性水平。

(6)
式中:e为模型(2)的拟合残差向量。记

(7)
此时,检验函数为
(8)
可以证明,上述统计量(4)和统计量(7)的构造均使用了最小充分统计量,且检验是一致最优势检验[3]。应当指出,当只存在单一粗差时,检验(5)和检验(8)分别等同于经典的Baarda检验[4-5]和Pope检验[6]。因此,可以认为上述2个检验是经典检验的推广。
粗差探测方法通过穷举所有可能的δ组合,使用检验(5)或检验(8)探测粗差。若同时有多个检验拒绝原假设,则通常取最大的T1(Y)或T2(Y)对应的δ确定粗差位置。
2 粗差探测能力度量指标
第1节中给出的粗差探测模型提供了一种基于最优势统计检验的粗差识别方法。该理论的另一项贡献是建立了定量分析“系统结构”蕴含的粗差探测能力的概念体系。
多余观测数是刻画系统结构强度的重要数量,其定义为[7-9]
(9)
式中:下标i表示向量Y中第i个数据对应的多余观测数,(·)ii表示矩阵第i行第i列处的元素值,i=1,…,m。
内部可靠性定义了最优势检验(5)和检验(8)可以探测的单个最小粗差(minimal detectable bias,MDB),内部可靠性被定义为[8,10-11]
(10)
式中:λ0=λ(α0,γ0),为在某个取定的第一类风险α0和检验的势γ0条件下的对应的非中心化参数;δi为向量Y中第i个数据为粗差时的示性向量,仅第i行为1,其他为0。
外部可靠性定义为未被探测的MDB对参数估计结果的影响[5,9,11]。由于粗差对未知参数估计的影响是一个向量,为刻画其大小,有2种度量方法:
①使用该向量的无穷范数,被称为最小可探测效应(minimal detectable effect,MDE):
(11)
②偏差噪声比(bias to noise ratio,BNR),用Cook距离来刻画[11]:
(12)
BNR反映了未探测的单个粗差对参数估计结果的影响相对于估计噪声的大小,因此BNR无量纲,但也难以说明通常情况下多大的BNR才算太大了。
3 飞行器测量数据粗差探测模型性能仿真与优化
单时刻模型利用多个测量通道的同步观测数据探测粗差。以测距雷达为例,设第u个时刻,多台测距雷达获得目标的多个斜距观测量Rv(tu),其中v表示第v台测距雷达。按照斜距观测方程的定义,可将观测方程在目标概略位置处线性化,可得到单时刻粗差探测模型:
R=H·Δx+δΔ+ε
(13)
式中:R为由第u个时刻所有斜距观测量Rv(tu)减去初值后构成的向量;H为模型线性化展开所得的梯度矩阵;Δx为待求概略位置改进量;ε为误差,设其为高斯噪声;δ和Δ的定义同式(2)。
单测量通道模型将单个测量通道观测数据按照观测时间先后进行排列形成时间序列数据,然后利用多项式模型对数据进行建模,从而建立粗差探测模型,以下简称其为单通道模型。设第v个通道在时刻tu的斜距观测数据Rv(tu)的离散时间模型为
(14)
式中:ζk为多项式系数,Rv(tu)为第v个雷达在时刻tu的斜距观测量,θk(·)为正交多项式,q为多项式阶数,εv(tu)为误差。
模型(14)为线性模型,若在模型中考虑粗差并写为矩阵形式,可得单通道粗差探测模型:
T=Ca+δΔ+ε
(15)
式中:T为由单个雷达的Rv(tu)按时间排列形成的向量,C为正交多项式基定义的已知矩阵,a为待估计的多项式系数。
多时刻多测元联合模型将目标位置在短时间内的变化建模为形如(14)的多项式,然后联合多个测量通道多个时刻的数据建立粗差探测模型,以下简称其为联合模型。设短时间内目标位置的变化可以用多项式模型表达:
(16)
式中:x(·),y(·),z(·)为目标的三维空间位置;φx,k,φy,k,φz,k为三方向上多项式系数。
将式(16)带入斜距测量方程,且将方程在概略点b0处线性化展开,其中b0为三方向上系数初始值排列而成的向量,由此可得粗差探测模型:
F=G·Δb+δΔ+ε
(17)
式中:F为多测量通道多时刻斜距观测量减去初值后排列而成的向量,G为梯度矩阵,Δb为待估计的多项式系数改进量。
3.1 多粗差探测性能仿真分析
为比较上述3种模型的粗差探测能力,按照典型测量方案生成了仿真数据,以定量比较3种不同模型在实际应用中的粗差探测能力。仿真场景取定为典型航迹和观测几何,取50 s时长数据,采样率20 s-1,测站数为9个。对同一组含粗差的仿真数据,分别使用上述模型进行粗差探测,然后比较不同模型粗差探测漏检率、虚警率、内部可靠性、外部可靠性、系统冗余观测数等定量指标。
对于单通道模型和联合模型,时间窗口取为1 s,这样可按照时间窗口将数据分为50个子组,子组的编号记为d,此时子组编号的取值范围为d=1,2,…,50。分别用3种模型对其建模:①每子组数据可建立联合模型1个,每个模型含观测值180个;②每子组的数据还可建立单通道模型9个,每个模型含观测值20个;③每子组的数据可建立单时刻模型20个,每个模型观测值9个。
如果数据中只有单个粗差,那么按照检验(5)和检验(8)进行粗差探测时,其探测策略是清晰的。若同时有多个检验拒绝原假设,取检验统计量最大的δ确定粗差位置即可。但是如果数据中有多个粗差,本文按照以下方法进行多粗差探测。
设单个数据是粗差的发生概率为一定值p0,对于数据个数为m的模型,设其包含的粗差个数为p,则其粗差个数正好为k的概率为P{p=k}=b(m,p0,k),k=1,…,m。当k>mp0时,b(m,p0,k)为一单调递减函数,此时应按照单个粗差假设开始探测数据,直至某个预定的粗差个数上限停止搜索。本文建议粗差探测搜索遍历的粗差个数上界按照以下公式计算:
(18)
式中:s是粗差搜索数的上界,P0为某个取定的探测失效概率。
由于式(18)不具有计算上的便利性,并考虑到当k>mp0时,b(m,p0,k)为一迅速下降函数,因此可以利用以下近似公式计算s:
(19)
注意到,在检验(5)和检验(8)中,若取定p时,要比较2种不同备选假设(按δ的定义不同而形成不同的备选假设)的检验量显著性,只需比较其大小即可,因为这些检验量都是服从同一分布的。若p取不同值可按照如下方法处理。以检验(5)为例讨论这一问题,检验(8)可类似解决。
对符合式(4)的p取不同值(设其分别为p1和p2)的2个统计量其在原假设下的分布为
T1,p1~χ2(p1),T1,p2~χ2(p2)
(20)
其拒绝域分别为
(21)
在T1,p1和T1,p2同时落在拒绝域,即满足式(21)时,本文建议按照如下公式比较两者之间的显著性:
(22)
式中:f(x)为统计量T的概率密度函数,p为自由度,T为式(20)中定义的统计量。按式(22)分别计算S(T1,p1,p1)和S(T1,p2,p2),取S值较小的统计量T为更显著统计量。
定义漏检率为未识别的粗差个数占总粗差个数的比率,记其为LM;定义虚警率为误识别为粗差的数据占总正常数据的比率,记其为LF。表1给出了几种不同模型的漏检率和虚警率的比较。其中,单通道模型1和单通道模型2分别是采用一次多项式和二次多项式对数据建模的结果。从表1可以看到,除联合模型外的其他几种模型粗差探测准确性相近。

表1 几种典型粗差探测模型性能
按照近似公式(19),取P0=0.01时,可计算得到单时刻模型需要搜索的粗差数为1,单通道模型为2,联合模型为5。由于单时刻模型和单通道模型的数据规模较小,因此其需要搜索的备选假设数也比较少。而对于联合模型,为达到与另外2种模型相同的失效概率,其最大搜索的备选假设约为1.5×109组,这在计算上是不可接受的。表1中给出的结果实际上只搜索到最多3个粗差,其备选假设共9.7×105组,在PC机上耗时约2 h。本研究还分别比较了最大搜索数为1个、2个、3个粗差的联合模型的粗差探测准确性,发现其漏检率和虚警率随着最大搜索粗差数有小幅度提高,但变化不明显。对于最大搜索数为4个、5个粗差的联合模型则因为计算量级太大而没有进行实验。这些结果说明,模型包含的数据较多对粗差探测问题是不利因素,此时多粗差发生的概率显著变大,这意味着数据污染的可能组合更复杂,备选假设组合的量级急剧变大,导致不能接受的计算复杂度,由此导致粗差探测准确性降低。
为比较单通道模型在不同测量通道上的粗差探测能力是否有明显差异,使用单通道模型对不同测量通道的仿真数据进行粗差探测,统计其漏检率和虚警率,结果见表2。从表2可以看出,虽然不同测量通道的粗差探测模型结构完全相同,但粗差探测准确性差别较大,受到粗差数据的分布和量级等多种因素的显著影响。

表2 单通道模型1的不同通道之间粗差探测性能
根据以上结果,可以得出如下结论:①随着粗差个数增加,基于最优势检验的多粗差探测模型,探测效率下降很快,因此在存在多粗差的场合,使用小数据集模型更好;②随着模型中的粗差个数增多,需要搜索的备选解急剧增加,这会导致不能接受的计算复杂度。上述2种因素使得基于多粗差探测的统计检验模型在实用性上具有诸多限制。
3.2 单粗差探测能力的定量评估与模型优化设计
由于不同模型使用的数据集规模不同,不能直接利用本文第2节的指标比较不同模型之间的粗差探测能力。本文使用如下公式获得单时刻模型、单通道模型等效于联合模型的MDE、MDB和冗余观测数r:
(23)
式中:由一组联合模型的观测数据可以建立多组单时刻模型或单测元模型,设其组数为G,则式(23)中g=1,…,G,h为每个子组中的观测值编号;Be,Ee,Ne,re分别表示子组的等效MDB、等效MDE、等效BNR和等效多余观测数。
图1为几种模型之间的MDB值对比。图中,d为数据集编号。从图1可以看出,单通道模型1比单通道模型2的最小粗差探测能力要强,这是符合直觉的,因为在模型表示误差受控的条件下,一次多项式比二次多项式要紧致,因此使用一次多项式的单通道模型具有更强的最小粗差探测能力。但是从表1中的结果来看,二次多项式的单通道模型具有更优的粗差探测能力,这种现象不好解释,本文将其归结为仿真实验中粗差分布和量级的不确定性在漏检率、虚警率上形成的随机波动效应造成的结果。图1中单通道模型的等效MDB值为一水平直线,这表明单通道模型的结构不随数据集变化而变化,由于数据集是按时间顺序排列的,也就是单通道模型的结构不随时间变化,图3和图4都反映了这一事实。图1还表明,单时刻模型和联合模型的最小粗差探测能力要强于单通道模型,因此单时刻模型和联合模型的结构更好,其中联合模型的结构达到最佳。
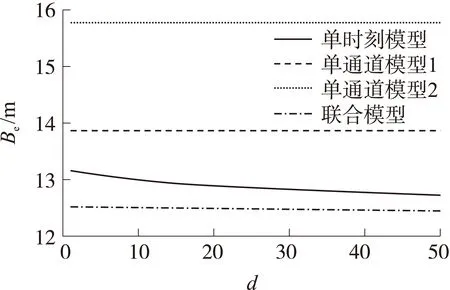
图1 不同模型的等效MDB
由于不同模型的参数空间定义不同,因此不同模型的等效MDE值不能直接比较。注意到,可将联合模型参数估计误差等效为目标空间位置误差,然后可比较其与单时刻模型的等效MDE。

(24)
(25)
为联合模型位置参数的等效MDE。
图2是单时刻模型与联合模型的位置参数等效MDE值的比较。从图中可以看到,未探测最小粗差对单时刻模型的影响较大,就这个意义上说,联合模型从结构上是要优于单时刻模型的。

图2 位置参数等效MDE
图3为几种模型之间的BNR值的对比。图中单时刻模型的BNR值最大,这反映了该模型受到未识别的最小粗差的影响最为显著,这一结论与上述关于MDE的分析相同。但在比较BNR值时应注意单时刻模型的待估计参数为位置,而其他几种模型的待估计参数为多项式系数。图3中反映的联合模型和单测元模型之间的结构优劣是与图1一致的。

图3 不同模型的等效BNR
冗余观测数反映了系统的每个观测量对决定最终参数估计结果时所起的作用,越大的冗余观测数意味着越好的系统结构。图4给出了几种模型的冗余观测数对比。从图可以看出,联合模型具有最优结构,其次是单通道模型1和单通道模型2,单时刻模型最差。

图4 不同模型的等效冗余观测数
综合上述分析可知,理论上无论是粗差探测还是参数估计,联合模型都具有最优结构,但从粗差探测的实际应用效果来看,联合模型并非最佳。其原因在于联合模型的观测值个数较多,因此同时出现多个粗差的概率较高,导致其粗差探测效果较差。为获得最优粗差探测模型,应取观测值个数适中的模型才能获得最优应用效果。
基于上面的考虑,本文将联合模型的时间窗口tw取为不同长度,考察在不同数据集规模条件下的联合模型粗差探测能力和计算时间t0。表3给出了几种取不同时间窗口大小的联合模型粗差探测能力的对比数据,表中,m为式(1)中的维数,s为式(18)中定义的粗差探测遍历搜索个数的上界。从表中可以看到,随着时间窗口变小,联合模型观测数据个数变小,系统的粗差探测成功率有所提高,逐步接近于单时刻模型和单通道模型。
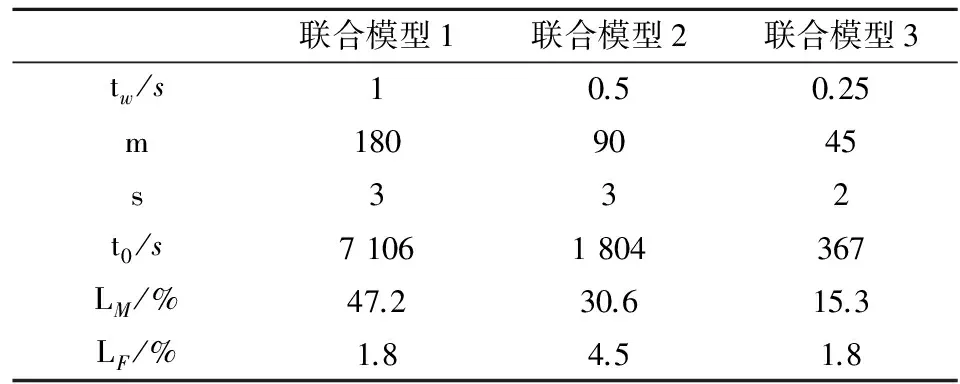
表3 时间窗口取值不同的联合模型粗差探测性能
图5~图8分别给出了上述几种联合模型的等效MDB、等效MDE、等效BNR和冗余观测数随时间窗口长度的变化。从图中可以看到,随着时间窗口变小,联合模型的等效MDB和等效MDE逐渐增大,并向单时刻模型靠近。等效BNR和冗余观测数也反映了与等效MDB和等效MDE相一致的信息。

图5 不同联合模型的等效MDB

图6 不同联合模型的等效MDE

图7 不同联合模型的等效BNR

图8 不同联合模型的等效冗余观测数
根据上述结果,可得出如下结论:在上述3种模型中,多测量通道多时刻联合模型具有最优的单粗差探测能力,因此在实用中应尽量采用联合模型探测粗差,并根据粗差发生的统计特性对联合模型的时间窗口长度进行设计,选用大小合适的模型。
4 结论
本文利用粗差探测能力度量理论,对几种典型的飞行器航迹测量数据的粗差探测模型进行了定量评估和仿真实验。研究表明,模型结构对系统的粗差探测能力影响明显,在工程应用中设计粗差探测模型时,应根据粗差发生的统计特征选取数据量大小合适、结构强度高的模型。本文研究成果提供了一种可以参照的模型优化设计方法。
[1] 刘利生.外弹道测量数据处理[M].北京:国防工业出版社,2002:79-97. LIU Li-sheng.Post-flight data processing of trajectory measurement[M].Beijing:National Defense Industry Press,2002:79-97.(in Chinese).
[2] 王正明,王宝智.异常观测数据的逐点剔除法[J].数学的实践与认识,1997,27(3):266-274. WANG Zheng-ming,WANG Bao-zhi.One by one-method of outliers rejection in linear regression model[J].Mathematics In Practice and Theory,1997,27(3):266-274.(in Chinese)
[3] KARGOLL B.On the theory and application of model misspecification tests in geodesy[D].Bonn,Germany:Institute for Geodesy and Geoinformation,University of Bonn,2007.
[4] BAARDA W.Statistical concepts in geodesy[J].Geodesy New Series,1967,2(4):22-25.
[5] BAARDA W.A testing procedure for use in geodetic networks[J].Geodesy New Series,1968,2(5):11-15.
[6] POPE A J.The statistics of residuals and the detection of outliers[R].Rockville,Maryland:US Department of Commerce,National Geodetic Survey,1976.
[7] SNOW K B.Applications of parameter estimation and hypothesis testing to GPS network adjustments[D].Ohio:The Ohio State University,2002.
[8] 王金岭,陈永奇.论观测值的可靠性度量[J].测绘学报,1994,23(4):252-258. WANG Jin-ling,CHEN Yong-qi.On the reliability measure of observations[J].Acta Geodaetica et Cartographica Sinica,1994,23(4):252-258.(in Chinese)
[9] SCHAFFRIN B.Reliability measures for correlated observations[J].Journal of Surveying Engineering,1997,123(3):126-137.
[10] TEUNISSEN P J G.Minimal detectable biases of GPS data[J].Journal of Geodesy,1998,72(4):236-244.
[11] GUO J F.Reliability analysis for a robust M-estimator[J].Journal of Surveying Engineering,2011,137(1):9-13.
Method of Optimally Choosing Gross-error Detection Model
TU Xian-qin1,2,GU De-feng2,YI Dong-yun2,ZHOU Hai-yin2
(1.Unit of PLA 91550,Dalian 116023,China;2.Department of Mathematics and System Science, College of Science,National University of Defense Technology,Changsha 410073,China)
To evaluate the gross-error detection performance of different models,the redundancy number,internal and external reliability index etc.were introduced to quantitatively compare and analyze the gross-error detection performance of three typical models used in the aircraft tracking-data process.The equivalent rules for index comparison between different models were established;the simulation experiment in conformity with the actual engineering application was carried out.The results show that the model using a larger data set has stronger structural strength and better single gross-error detection performance,but it is drawback to gross-error detection.It is suggested that in practice,the model with stronger structural strength and the proper size is chosen as the optimal model according to the statistical characteristics of gross-error occurrence.
track measurement;gross error;system modeling;optimization model
2016-07-20
国家自然科学基金项目(61370013;91438202)
涂先勤(1979- ),男,博士,研究方向为外弹道测量数据处理方法。E-mail:tuxq79@163.com。
V248.1
A
1004-499X(2017)01-0022-06
