突发需求下的三级供应链协调分析*

王青云， 张捍东

(1.安徽工业大学 工商学院，安徽 马鞍山 243002;2.安徽工业大学 电气与信息工程学院，安徽 马鞍山 243002)

突发需求下的三级供应链协调分析*

王青云， 张捍东**

(1.安徽工业大学 工商学院，安徽 马鞍山 243002;2.安徽工业大学 电气与信息工程学院，安徽 马鞍山 243002)

针对市场需求突发情况，建立了一个基于预测补货的控制系统模型，并运用控制论思想，对供应链系统进行协调控制；仿真结果表明系统能有效降低市场不确定性对供应链的影响，为供应链管理决策提供理论参考。

供应链协调；控制模型；突发需求

随着经济全球化发展，以市场需求为导向、以核心企业为中心，由客户、制造商、分销商和零售商组成的供应链随之产生。供应链与供应链的竞争成为企业在市场上获得成功的一个重要因素。供应链的经营与运作模式成为理论界和实业界的关注热点。伴随着经济的快速发展，市场需求的不确定性也随之增加。在自然条件恶劣的情况下，市场环境容易受到自然灾害的影响，引起产品需求突变。如2011年泰国洪灾，使生产线被淹，产能受重创，引发全球硬盘上涨。引起需求环境变化的因素，可以从两个方面分析：一是产品供应量减少，为了应对原本需求量较大的市场，产品涨价；二是由于洪灾的影响，外界企业或单位为了避免缺货，出现大量囤货行为，引起需求短期大幅上涨。又如，由于生产同类产品或可替代产品的企业停产倒闭，消费者会大量涌入正常运营的供应链企业，购买产品，引起需求环境突变。但随着时间的推移，市场需求会逐渐回归于常态，需求突变常常呈现出正态变化规律。

在供应链的流通领域中，供应链相邻节点企业之间各有不同的库存管理策略，存在信息不能完全共享，管理过程中衔接和运作不确定性等问题。下游需求信息逐级向上游传递，库存波动量大，不可避免地产生需求的扭曲现象，即牛鞭效应，从而导致供应链库存积压、对市场需求反应迟钝。在供应链管理过程中，库存管理作为一项十分重要的内容，其费用往往占到总成本的20%～40%[1]。过量的库存积压，会降低供应链中节点企业对外界环境变化反应的快速性和灵活性。库存的高低不仅影响着单一企业的综合成本，而且制约着整条供应链的性能。因此，供应链环境下多级库存的控制和相邻节点企业间的协调问题就成了目前研究的热点。

文献[2]研究了基于博弈双方均为风险中性的一个二级供应链应对突发事件的协调问题；文献[3]在价格和市场需求不确定的环境下，研究了期权式契约在两阶段供应链中的协调作用；文献[4]研究了随机需求环境下销售商采取定价延迟策略对供应链系统成员的最优决策和利润。文献[5]研究了随机需求下多生产商与多零售商组成、生产和销售多种产品的供应链如何应对需求扰动问题，建立了变分不等式模型，说明了供应链竞争力取决于整条“产销链”的效率，管理者应提高链内成员的运作效率与协同性，准确的需求预测和快速反应能力有助于保证供需平衡，能有效降低需求扰动带来的风险；文献[6]针对牛鞭效应及其时滞成因，基于供应链库存的内部系统动力学机制，提出一类新的基于库存波动状态的动态库存控制策略，将策略的参数优化求解问题转化成线性矩阵不等式的求解问题；文献[7]研究了供应链季节性需求的随机变异性，得出在处理牛鞭效应、库存波动率等方面采用平滑补货规则优于传统；文献[8]研究了多供应商和单制造商组成的二层供应链调度问题，运用多目标优化和多属性决策相结合的方法设计供应链调度决策方法；文献[9]针对由两个供应商和两个零售商组成的二级供应链系统，分析两个供应商发生供货中断的4种情形及订货量决策模型；文献[10]研究供应链的结构因素(即层次、节点数目的链接的数量和分布)对其动力学性能(即牛鞭效应)的影响。结果表明在市场需求的突然冲击下，供应链的节点数和供应链的发散影响供应链绩效；文献[11]研究供应链在原材料生产、半成品生产以及市场需求不确定情况下的风险共担契约与模型；文献[12]根据突发事件造成市场规模变化大小，采用收益共享契约调节供应链；文献[13]研究了由一个制造商、一个分销商和一个零售商组成且零售商占据主导地位的三级供应链系统的应急需求协调问题，针对突发需求重新设计回购契约函数，实现供应链系统在突发需求情形下协调；文献[14]提出了不充分的信息管理策略，以缓解供应链中断风险，结果表明了供应链在应对外界不确定风险时协同规划、预测与补货与完整的信息使系统工作状态表现更好。学者对供应链管理的研究大多基于博弈论和运筹学，制定相关契约供应链上下游制约，通过上下游信息共享应对市场不确定性和降低牛鞭效应，以得到最优订货策略或利润最大化。为了应对市场需求环境的不确定性和需求突变，供应链上下游应实现信息完全共享，增强互相帮助互相依赖的密切配合，共同应对外界变化和竞争，以提高供应链整体优势和应对外界市场突变风险的能力。实际供应链在运作过程中，信息完全共享实现较困难，如供应链各单位库存或销售情况很难完全共享，针对这种情况，研究表明通过预测补货和供应链协同规划能更好地应对市场的不确定性和需求突变。

基于供应链的运行模式和管理机制，考虑了上下游信息不完全共享的情况，采取预测补货的方式，建立了一个连续控制系统模型，在市场需求突发情况下，运用控制论思想，对供应链系统进行协调控制，以减小市场不确定性因素对供应链的影响，提高供应链风险应对能力，达到改善供应链整体绩效的目标。

1 供应链的建模过程

供应链由三级构成，分别是生产商、配货商(中转站)和零售商。

生产商根据供应链下游两级(配货商(中转站)和零售商)提供的产品订货情况和销售信息，结合市场需求预测和生产原料的供给情况，安排所需原料的订购，制订生产计划，以满足下游订货的需求量。配货商根据上游成品供给和下游产品订购情况，为获得最佳服务质量和最大利益，合理制定配送方案，负责将生产商生产出的成品配送给各零售商。在供应链中，配货商的作用至关重要，配货商可以统筹供应链的整体服务、绩效、整体方案和规划，协调上游(生产商或原材料供应商)和下游(各零售商)，应对市场波动，提高供应链的市场反应速度和竞争能力。零售商根据上游的供货情况和市场需求，合理安排产品订购，制订销售计划，销售产品，避免缺货。缺货打击购买者的购物信心，影响服务质量，进一步影响后续的销售。平滑的库存决策规则已被公认为是消除牛鞭效应最有效的方法[7]，采用预测方法进行补货，以提高系统绩效。

1.1 生产商的模型建立

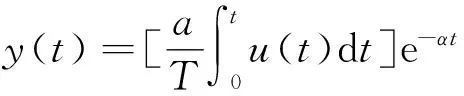
1.2 配货商的模型建立

1.3 零售商的模型建立

2 基本供应链系统模型

供应链系统由生产商、配货商、零售商三级组成，系统流程如图1。系统的输入量和输出量分别为原材料输入量u、成品售出量y。

图1 供应链流程Fig.1 Supply chain process

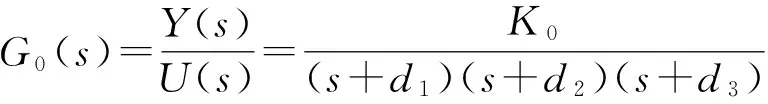
一般情况下，生产商对原料的订购根据对市场需求的预测和下游的订货情况，供应链系统模型的输出体现市场需求变化，系统模型的输入体现生产商的原料订购情况，故在上述开环系统模型的基础上引入反馈F(s)，得到供应链闭环系统模型，其闭环传递函数G(s)为

(1)

3 有需求干扰的供应链系统PID控制模型及仿真

通常市场受到环境不确定因素的影响，容易出现需求突变，需求变化常常呈现为正态规律变化，具体反映在供应链模型中输出量会出现指数增长和指数衰减的情况。

供应链上下游各企业原本在稳定市场环境下按计划稳定运营，由模型传递函数G(s)反映供应链模型稳定运营情况。由于市场需求突变，引发供应链末端的出售量突变，即模型输出扰动ΔG(s)，产品销售量增大即模型输出突变，反馈到输入端，通过控制器Gf(s)调节系统G(s)的原料输入量，相应地生产商和配货商对生产率和运输率调节，零售商对销售方案进行调节。通过调整相关参数，制定合理方案安排生产，通过相互配合，快速反应来灵活地应对市场需求的不确定性。

PID控制器在系统过程控制中，采用偏差的比例(P)、积分(I)和微分(D)进行控制，在自动控制领域应用广泛。它具有控制参数独立、易于实现、原理简单，参数的选定方便易操作等优点。比例环节可以减小控制过程的静态偏差，积分部分可以消除系统的偏差，微分环节可以减小超调量，克服振荡，有助于加快系统的跟踪速度，使系统趋于稳定。为了改善系统的性能，控制器Gf(s)采用PID调节系统建立的模型。

3.1 有需求扰动的供应链系统PID控制模型

控制器Gf(s)采用PID控制调节系统，建立有需求扰动的PID控制模型，如图2。

图2 闭环PID控制模型Fig.2 Closed loop PID control model

系统闭环传递函数H(s)为

(2)

其中，PID控制环节Gf(s)=Kp[1+Tds+1/(Tis)]；式(1)表示G(s)，取F(s)=Kf/[Tf(s+αf)]。干扰主要由市场需求波动引起，这里选取呈指数规律衰减，表示为ΔG(s)=c/(s+α)，参数α取正值，c可取正值也可取负值，根据有需求扰动的PID控制模型(图2)，若输出扰动引起模型输出呈指数规律增加，则c取负值；若输出扰动引起模型输出呈指数规律减小，则c取正值。

若供应链模型不采用PID控制，可取Gf(s)=1，则无PID控制的供应链模型闭环传递函数H0(s)为

(3)

3.2 有需求扰动的供应链系统模型的仿真验证

为了验证供应链PID控制模型的良好性能，分别对系统模型G(s)、无PID控制有需求扰动的系统模型H0(s)和PID控制模型H(s)进行单位阶跃响应性分析。

现对需求突变引起模型输出突变减小的情况进行仿真分析。

首先，仿真分析市场没有出现需求突变的情况。供应链模型G(s)的运作性能。取a1=a2=1，a3=1.2，T1=T3=10，T2=2，α1=α2=α3=0.1,Kf=-1，Tf=600，αf=0.08，其单位阶跃响应曲线如图3，其中虚线曲线代表无PID无扰动下以模型G(s)正常稳定运行的单位阶跃响应曲线。

图3 闭环PID控制模型的阶跃响应分析Fig.3 Step response analysis of closed loop PID control model

然后，仿真分析有需求突变ΔG(s)的情况。分别对采用PID控制的模型H(s)和没有采用PID控制的模型H0(s)的运作性能进行对比分析。选取a1=a2=1，a3=1.2，α1=α2=α3=0.1，T1=T3=10，T2=2，Kf=-5，Tf=100，αf=0.05，c=5，α=7，图3中点线曲线代表无PID控制的系统模型H0(s)的单位阶跃响应曲线；选取Kp=5，Td=4，Ti=30,Kf=-2，Tf=100，αf=0.05，c=5，α=7，图3中实线曲线代表采用PID控制的闭环系统模型H(s)单位阶跃响应曲线。

从图3中不难发现，虚线曲线运行平稳无振荡，表示在合理设置参数的情况下，无PID无扰动下以模型G(s)正常运行稳定，缺点是有少许缺货，可以通过适当调节销售价格减小缺货情形。对比图3中实线曲线和点线曲线，虽然最终都达到平稳运行，但不难发现，实线曲线较快地实现系统平稳运行，且超调量较小，针对单位输入，输出也基本达到单位输出，能够较快地实现输入输出跟随性能，无库存积压，牛鞭效应也很小。相比之下，点线曲线表现出超调量大，在开始的时间内有较大的周期波动，很大程度上降低了系统平稳快速反应的灵敏性，使系统陷于振荡状态，对系统应对现代快速变化的需求市场不利。在应对外界市场需求突变方面，采用PID调节的供应链系统更能表现出平稳快速反应的良好性能。

综上，介绍了供应链三级模型的建立过程和模型仿真验证，表明供应链上下游企业在信息不能完全共享的条件下，通过各级预测和恰当地选取模型内的相关参数，使得模型能够运行平稳，性能较好。在需求扰动情况下，可以通过调节T或a等类型的相关参数，使得模型协调稳定，降低了系统的牛鞭效应，提高了供应链整体性能。

以供应链整体绩效为目标，通过分析各环节的相互影响因素，针对市场需求突发情况，运用控制论思想，提出了一种供应链协调控制模型，对三级供应链进行了协调控制分析，同时通过计算机仿真验证了系统模型的可行性，为提高供应链管理决策和科学实施提供了理论参考。系统中突发需求在一定范围内可实现有效调节，若超出供应链中各企业方案要求的安全范围，性能可能不理想。

[1] BALLOU R H.Business Logistics Management[M].Prentice-hall Englewood Cliffs N J,1992,81:125-130

[2] 吴忠和,陈宏,赵千.不对称信息供应链应对突发事件协调模型[J].系统管理学报,2015,24(1):91-97

WU Z H,CHEN H,ZHAO Q.Supply Chain Coordination Model under Asymmetric Information and Disruptions[J].Journal of Systems & Management,2015,24(1):91-97

[3] 李琳,范体军.不确定环境下两阶段供应链的期权式契约协调[J].系统工程学报,2012,27(6):812-822

LI L,FAN T J.Coordination by Option Contract in Two-echelon Supply Chain[J].Joumal of Systems Engineering,2012,27(6):812-822

[4] 张克勇,侯世旺,周国华.不确定需求下供应链定价延迟策略研究[J].管理工程学报,2014,28(1):195-201 ZHANG K Y,HOU S W,ZHOU G H.Price Postponement Strategy in the Supply Chain under Uncertain Demand[J].Journal of Engineering Management,2014,28(1):195-201

[5] 徐兵,蒋昆.多商品流供应链网络应对随机需求扰动研究[J].运筹与管理,2014,23(6):144-151

XU B,JIANG K.Study on the Multi-commodity Supply Chain Network Coping with Random Demand Disruption[J].Operations Research and Management Science,2014,23(6):144-151

[6] 李翀,刘思峰,方志耕,等.供应链网络系统的牛鞭效应时滞因素分析与库存控制策略研究[J].中国管理科学,2013,21(2):107-113

LI C,LIU S F,FANG Z G,et al.Bullwhip Effect in Supply Chain Networks with Lead Time Delays and Its Inventory Control Strategy[J].Chinese Journal of Manegement Science,2013,21(2):107-113

[7] FRANCESCO C,GRAVIO D,GIULIO,et al.Smoothing Inventory Decision Rules in Seasonal Supply Chains[J].Expert Systems With Applications,2016,44:304-319

[8] 裴军,刘心报,范雯娟,等.基于生产与运输集成的供应链调度优化问题[J].中国管理科学,2012,20:586-593

PEI J,LIU X B,FAN W J,et al Supply Chain Scheduling Optimization Problem Based on Integration of Production and Transportation[J].Chinese Journal of Manegement Science,2012,20:586-593

[9] 汪传旭，许长延.两级供应链中供应中断情形下零售商转运策略[J].中国管理科学,2015,23(2):70-79

WANG C X,XU C Y.Retailer Transshipment Policy with Supply Disruption in a Two Stage Supply Chain[J].Chinese Journal of Manegement Science,2015,23(2):70-79

[10] DOMINGUEZ R,CANNELLA S.The Impact of the Supply Chain Structure on Bullwhip Effect[J].Applied Mathematical Modelling,2015,39(23-24):7309-7325

[11] 彭红军,周梅华,刘满芝.两级生产与需求不确定下供应链风险共担模型研究[J].管理工程学报,2013,27(3):156-163

PENG H J,ZHOU M H,LIU M Z.Research on Risk Sharing Model in Supply Chain with Uncertainties in Two-level Yields and Demand[J].Journal of Engineering Management,2013,27(3):156-163

[12] 覃艳华,曹细玉,阮平,等.突发事件下生产成本信息不对称时的供应链协调应对[J].华中师范大学学报(自然科学版),2013,47(2):259-264

QIN Y H,CAO X Y,WAN P,et al.The Coordination of Supply Chain in The Case of Asymmetrinc Information on the Manufacturing Cost and under Disruptions[J].Journal of Huazhong Normal University(Natural Science Edition),2013,47(2):259-264

[13] 霍艳芳,刘忠盛.突发需求下零售商占优型三级供应链协调分析[J].计算机集成制造系统,2014,20(4):954-962

HUO Y F,LIU Z S.Coordination Analysis on Retailer-Dominant Three-level Supply Chain under Disruption Demand[J].Computer Integrated Manufacturing Systems,2014,20(4):954-962

[14]YANG T J,FAN W G.Information Management Strategies and Supply Chain Performance under Demand Disruptions[J].International Journal of Production Research,2016,54(1):8-27

责任编辑：田 静

Coordination Analysis of Three-level Supply Chain under Disruption Demand

WANG Qing-yun, ZHANG Han-dong
(1. Industrial and Commercial College, Anhui University of Technology, Anhui Maanshan, 243002, China; 2.School of Electrical and Information Engineering, Anhui University of Technology, Anhui Maanshan 243002, China)

Focusing on the market disruption demand, a control system model is founded on the method of forecasting replenishment, and the control theory is applied to coordinating the supply chain system. The simulation results show that the system can effectively reduce the impact of market uncertainty on supply chain. A theoretical reference is provided for supply chain management decision.

supply chain coordination; control model; disruption demand

2016-05-25;

2016-07-13.

安徽省自然科学基金项目(KJ2011Z044).

王青云(1983-)，女，山东曹县人，讲师，硕士，从事供应链协调控制研究.

** 通讯作者：张捍东(1963-)，男，安徽桐城人，教授，博士，从事工程优化技术与应用研究.

10.16055/j.issn.1672-058X.2017.0002.015

F273

A

1672-058X(2017)02-0071-06