初中一次函数现实背景模型探究

摘要：数学根植于生活并应用于生活，数学模型来自于现实世界，模型思想的建立是学生体会和理解数学与外部世界联系的基本途径；探究一次函数现实背景模型，有利于学生理解一次函数中两个变量间的对应关系及其图象和性质，并利用一次函数的图象和性质解决实际问题.

关键词：一次函数；现实背景；模型探究

作者简介：周占锋（1963-），男，福建省龙岩市武平县，本科，高级教师，武平县教师进修学校中学教研室主任.数学建模是数学学科六个核心素养之一，而模型思想是初中数学的重要数学思想.数学课程标准（2011年版）指出：数学与人类发展和社会进步息息相关，随着现代信息技术的飞速发展，数学更加广泛应用于社会生产和日常生活的各个方面. 课标把模型思想作为十个核心概念之一，认为模型思想的建立是学生体会和理解数学与外部世界联系的基本途径.一次函数是初中学生学习和理解函数的重要素材，其中自变量与函数的对应关系是初学者理解两个变量间对应关系的难点，探究一次函数现实背景模型，有利于学生理解一次函数中两个变量间的对应关系及其图象和性质，并利用一次函数的图象和性质解决实际问题.以下是几种一次函数的现实背景模型探究.

一、行程问题的一次函数现实背景模型

设路程为s，速度为v，时间为t，则s=vt . 当速度v为常量，如v=30km/s，s=30t是正比例函数；而正比例函数是最特殊的一次函数. 若行程问题中出现两个或两个以上对象，不同时间段有不同的位置状态，就构成一次函数的分段函数模型.

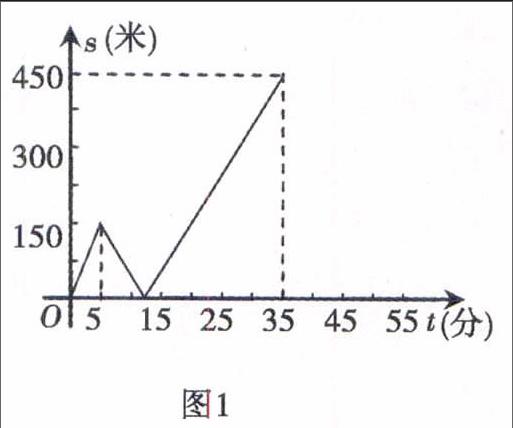
例1甲乙两人匀速从同一地点到1500米处的体检中心体检，甲出发5分钟后，乙以50米/分的速度沿同一路线行走，s关于t的函数图象的一部分如图1所示.设甲乙两人相距s（米），甲行走的时间为t（分）.

（1）求甲行走的速度；

（2）在坐标系中，补画s关于t函数图象的其余部分；

（3）问甲、乙两人何时相距360米？

分析此现实背景中出现甲、乙两人为两个不同对象，出发时间不同使各个时间段两人的相对位置不同，构成距离s与时间t在不同时间段有各自不同的一次函数对应关系，其中题设信息以文字信息和图象信息相结合的形式出现，从图象信息发现背景涉及四种不同情形：

①t=5分钟时甲走了150米；

②甲出发5分钟后，乙开始出发，t=12.5分钟时，甲追上乙，s=0；

③t=35分钟时，甲走了1050米；乙用时30分钟走了1500米，到达体检中心，s=450米；

④t>35分钟时，乙已到达体检中心，甲还要用15分钟走完450米的路程，t=50分钟时甲也到达体检中心，s=0.

根据以上分析s与t的函数关系式是：

s=30t（0≤t≤5）

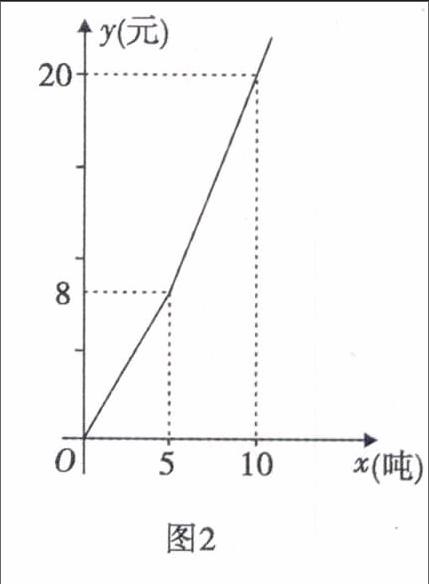
-20t+250（5

20t-250（125

-30t+1500（35

试题设计要点：

1.基础题设置：从图象信息中发现甲5分钟走的路程为150米，可求甲行走的速度为30米/分.

2.对实际问题的再现：t=35分钟时，乙实际用时30分钟，乙已经到达图书馆，此时s=450米，甲用时t=15分钟才能到达图书馆，此时s=0. 在坐标系中，补画s关于t函数图象的其余部分是连接（35，450），（50，0）的一条线段.

3.设甲、乙两人t分钟后相距360米，此处的难点是乙实际用时为（t-5）分钟，而不是t分钟，根据图象信息时间应在12.5

二、收费问题的一次函数现实背景模型

收费问题通常与两种或两种以上的收费方式相关，收费金额有的与时间建立一次函数关系，有的与用量建立一次函数关系.

例2（2014龙岩中考第23题）随着地球上的水资源日益枯竭，各级政府越来越重视倡导节约用水.某市对居民生活用水按“阶梯水价”方式进行收费，人均月生活用水收费标准如图2所示.图中x表示人均月生活用水的吨数，y表示收取的人均月生活用水费（元）.请根据图象信息，回答下列问题：

（1）该市人均月生活用水的收费标准是：不超过5吨，每吨按元收取；超过5吨的部分，每吨按元收取；

（2）请写出y与x的函数关系式；

（3）若某个家庭有5人，五月份的生活用水费共76元，则该家庭这个月用了多少吨生活用水？

水费问题通常采用“阶梯水价”方式进行收费，水费与用水量建立一次函数的分段函数现实背景模型，考查学生从现实生活中抽象出一次函数模型的数学思考，并用数学思考进行问题解决的考量.

三、销售问题的一次函数现实背景模型

销售问题通常以何种销售、销售单价与销售量为现实背景模型出现，多数是利润与销售量建立一次函数关系的模型，关注利润的合理区间. 有时通过图象信息提供已知条件，考查学生的读图能力.

例3（2016龙岩中考第23题）某厂家在甲、乙两家商场销售同一商品所获利润分别为y甲、y乙（单位：元），y甲、y乙与销售数量x（单位：件）的函数关系如图3所示，试根据图象解决下列问题：

（1）分别求出y甲、y乙关于x的函数关系式；

（2）现厂家分配该商品800件给甲商场，400件给乙商场，当甲、乙商场售完这批商品后，厂家可获得总利润是多少元？

该题以图象信息显示问题背景，突现从实际生活中抽象出一次函数模型解决实际问题的能力，考查用解析法求解一次函数解析式.

四、图形运动的一次函数现实背景模型

图形运动通常有点动、线动和面动等，其构成的轨迹、距离、面积等可以用函数来刻画，初中数学常有用一次函数刻画图形运动的情况.

例4已知如图4，在矩形ABCD中，动点P从点B出发，沿BC，CD，DA运动至点A停止.设点P运动的路程为x，△ABP的面积为y，如果y关于x的函数图象如图5所示，则△ABC的面积是（）

A.10B.16C.18D.20

分析此模型是由点动而产生面动，观察图4，动点P从点B出发，到点C位置时△ABC的面积最大；动点P从点C运动到点D，△ABC的面积保持最大数值不变；从点D运动到点A，△ABC的面积由最大值变为0.这一变化过程在图5的函数图象中得到充分刻画.由图5可知：BC=4，DC=AB=5，S△ABC=12×4×5=10答案是A.

现实背景模型的探究和建立饱含了教师的智识，教师只有不断加强业务学习，细心观察和品味现实生活中的事物关联性才能使教学有的放矢，课标对建立和求解模型的观察作了很好的阐述：从现实生活或具体情境中抽象出數学问题，用数学符号建立方程、不等式、函数等表示数学问题中的数量关系和变化规律，求出结果并讨论结果的意义.函数教学中重视现实背景模型的探究，有利于学生理解函数的概念，掌握从现实背景中抽象出函数模型的方法，学会用函数思想刻画事物的变化规律，提高课堂教学的有效性.