基于流变参数反演的高面板坝长期变形预测

李远程，张利娟，周 伟，马 刚

(1.黄河勘测规划设计有限公司，郑州 450003；2.武汉大学，武汉 430072)

1 研究背景

随着混凝土面板堆石坝坝高从200 m级向300 m级跨越，其堆石体的变形将不可避免地出现较大的增长。我国已建的200 m级高坝中发生了由于堆石体变形过大，导致混凝土面板裂缝偏多、局部挤压破损，周边缝位移值高等病害。因此，如何正确预测坝体在各种工况条件下的变形趋势，并在此基础上优化坝体的设计；或对已建成高坝坝体进行运行性态评价意义重大。

众所周知，堆石体在加荷后首先产生一定的瞬时变形，然后是随时间增长的流变变形，包括体积流变和剪切流变[1]，对于低坝后两种变形占总变形的比例较小，一般可以不予考虑，然而对于高面板堆石坝，其影响不容忽视，主要表现在由于堆石体流变变形的存在，使后期变形量较大，对面板及趾板等防渗体结构造成很大的安全隐患，严重影响面板坝的后期运行效益，且随着坝高的不断增高，其影响程度也越来越大[2]。由已建成的混凝土面板堆石坝的安全监测结果显示，许多情况下堆石体的流变变形都比较明显，这种附加的后期变形必然会对面板、接缝的应力、周边缝变形状态带来较大的影响。虽然现在基于试验的经验流变模型[3-5]已经应用到堆石坝的研究之中,但参数取值则存在着很大的不确定性：现场原位试验技术虽然广泛采用，但试验手段仍很单一，流变试验一般要长达几个月甚至一年以上[6]，野外操作具有很大的局限性；经过采集后的堆石试样，在人工的运输、转移等扰动因素下，已经很难测试出原始力学参数[7]；试验所用的天然的堆石材料与筑坝所采用的经过人工掺和后的堆石在级配上有很大的差别；堆石所处的天然应力场、温度场和渗流场在实验室很难真正地模拟；作为筑坝材料的堆石料最大粒径达到数10 cm到1 m量级，而室内三轴试验以直径30 cm、高度60 cm、允许最大粒径为6 cm最为常用，并且国际上还没有规模足够大的三轴仪，这样由于缩尺效应和试验点的相对有限，堆石材料的力学参数取值范围变化较大，在这种情况下，即使本构理论和计算方法非常准确精细，但依据的材料参数不准确，变形计算结果的可信度也就失去了保证。以面板堆石坝的现场观测的宏观信息(应力、位移、渗透水头等)为基础，通过智能算法反分析，可以获取堆石的流变参数[8]。

作者认为引起瞬时变形的静力本构模型参数由于国内外实验方法成熟[9]，参数的平行试验便于开展，且国内可供参考类比的工程实例和算例较多，取实验室值可信度较高，不必进行反分析率定。流变本构模型工程应用较少，国内工程参数资料匮乏，且直接影响大坝长期变形的分析，因此针对此重点反演。本文在对流变参数进行敏感性分析的基础上，选择对坝体变形敏感的参数作为待反演参数，采用基于最小二乘的遗传算法和有限元正分析构建反演平台，对水布垭面板堆石坝进行了流变参数反演分析，并预测了坝体变形稳定时的沉降值。

2 堆石坝的瞬时变形和流变变形本构模型

本文中采用邓肯E-B静力本构模型模拟大坝的瞬时变形，采用长江科学院提出的九参数幂函数流变模型模拟大坝的长期变形。

2.1 邓肯E-B静力本构模型

Duncan等对E-μ模型进行了修正[10]，采用切线体积模量Bt代替切线泊松比μt，该模型的切线弹性模量和切线体积模量的计算公式如下：

(2)

(3)

式中：Et、Bt分别为弹性模量和体积模量；Rf为破坏比；K为模量系数；n为模量指数；pa为单位大气压；c为凝聚力；φ为内摩擦角；Kb、m分别为体积模量系数和指数；σ1、σ3分别为大、小主应力。

在三维有限元计算中公式的用法和参数意义参考文献[11]。

2.2 九参数幂函数流变模型

长江科学院根据水布垭面板坝主堆石区茅口组灰岩堆石体流变试验成果，提出了幂函数本构模型，流变量与最终应力状态有关，剪切流变变形和体积流变变形公式如下：

εs(t)=εsf(1-t-λs)

(4)

εv(t)=εvf(1-t-λv)

(5)

最终轴向流变量εsf和应力水平sL、围压σ3之间的关系如下：

(6)

体积流变总量εVf和应力水平sL、围压σ3之间的关系如下：

εVf=cαSdαL+cβSdβLσ3λV=const

(7)

综上所叙，堆石体的流变特性可以由以上模型描述，该模型包括c、d、η、m、cα、dα、cβ、dβ、λV9个参数。

2.3 流变参数敏感性分析

流变模型的参数较多，若对每个参数都进行反演，计算复琐，影响反演效果，有必要进行参数敏感性分析。本文建立一均质土坝三维模型，在试验参数基础上，使一个参数缩放0.1～2.5倍，其余参数不变，按此标准遍历9个参数，对每一新组合参数进行有限元计算，分别输出大坝沉降值。定义敏感性因子为：

(8)

式中：k为灵敏度指标；yi为模型第i次计算输出值；y0为初始参数对应的模型输出值；xi为第i次计算时参数；x0为初始参数；n为计算次数。

由图1可知长江科学院幂函数本构模型中参数η、m对沉降敏感性低，为节省计算机内存，反演计算不予考虑；参数c、d、cα、dα、cβ、dβ、λv对沉降敏感性高，且dα、dβ和大坝沉降成负相关关系，因此下文反分析时只针对这7个参数反演。

3 基于遗传算法的流变参数反演

3.1 采用遗传算法进行流变参数反分析的流程

利用堆石体观测资料进行流变参数的反馈分析，其主要步骤如下：

(1)生成初始流变参数种群(假设规模为50个)，种群中每个个体为一组待反演的流变参数，结合本文，一个个体为一组7个流变参数(c、d、cα、dα、cβ、dβ、λv)的行向量，而每个流变参数为一个染色体。

(2)在第一代计算中，把每个个体带入有限元进行正分析，得到坝体的位移计算结果。

(3)在有限元计算结果中提取监测点所在位置的位移，和实际的位移监测成果进行最小二乘化，即构造适应度函数。

(4)在本代中所有的个体计算出适应度后，进行比较，选取适应值高的个体，进入下一代进行交叉和变异，再生成相同规模的样本。

(5)重复步骤(2)～步骤(4)，直至达到事先设定的最大进化代数，或最优值在连续两代内没有明显变化。

采用遗传算法进行参数反分析的基本流程图如图2所示。

3.2 反演分析的位移监测资料选取

为了使目标监测点位具有合理性且有代表性，选取水布垭面板堆石坝最大断面处(D0+212 m桩号)265.00和300.00高程的主堆石和下游堆石区的18个目标监测点SV01_1_13～SV01_1_22和SV01_1_23～SV01_1_30, 以此18个监测点2004年10月-2010年4月的大坝沉降数据系列作为反演样本，这些点分布于过渡料、主次堆石区，能够代表坝体沉降特征，且包含了沉降监测极值。

各点分布位置见图3，沉降时程曲线见图4～图5。

3.3 参数反演

水布垭面板堆石坝三维有限元网格见图6。

图3 D0+212.00断面监测仪器布置图Fig.3 Observation instruments layout at section 212

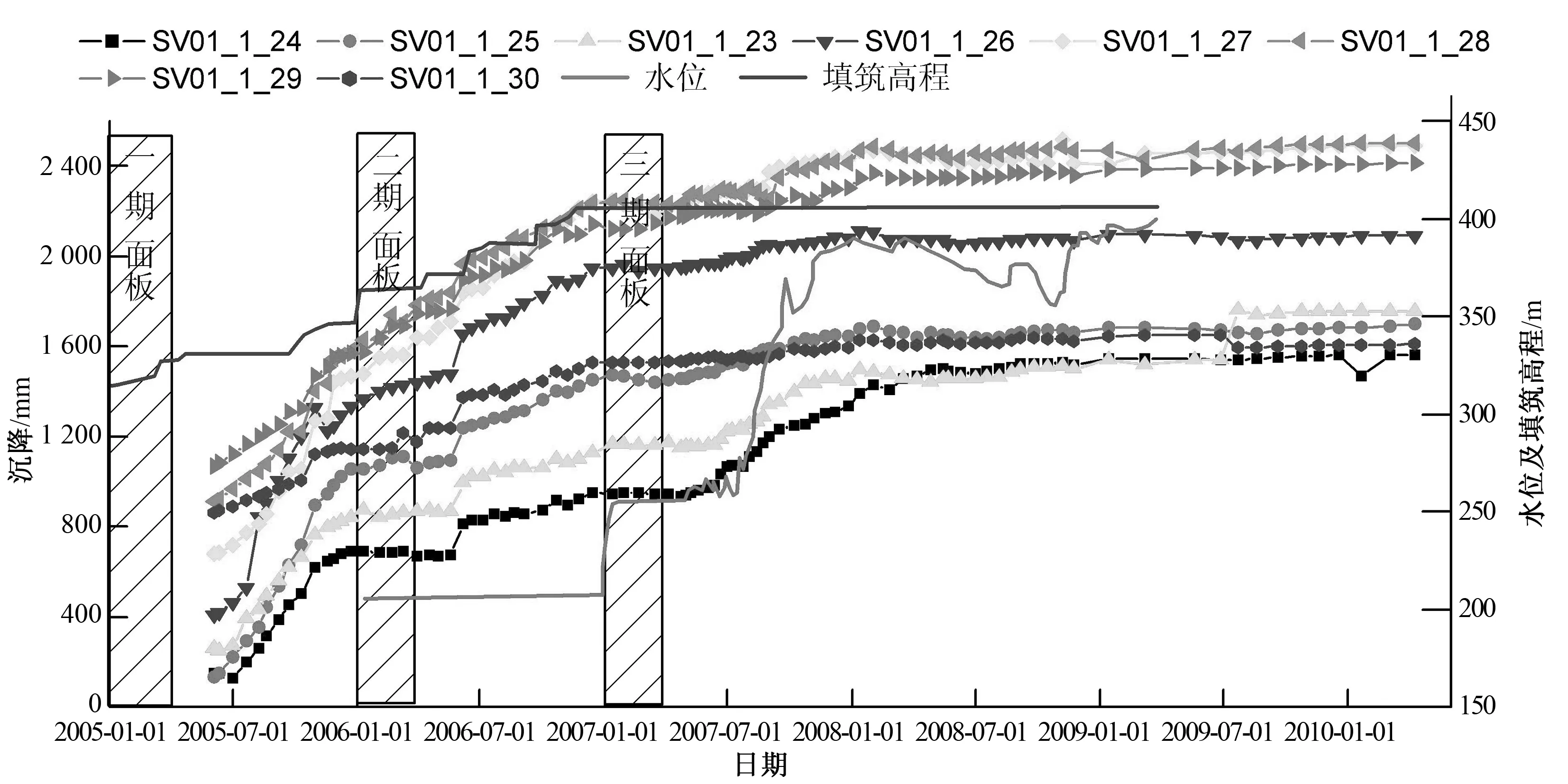
图5 0+212 m断面300 m高程监测点沉降时程线Fig.5 Internal settlements recorded at 300 elevation of section 212

图6 大坝三维计算网格图Fig.6 Three-dimensional finite element grid

设定参数的取值范围为各试验参数值的0.5～2倍，待反演参数的取值区间范围见表1。

种群规模：为了保证训练样本具有足够的代表性，用正交试验设计方法生成50组样本。

表1 堆石料待反演流变参数的变化区间Tab.1 Changing Ranges of parameters for back analysis

交叉概率pc控制着交叉操作进行的频度，pc较大可增强遗传算法初期搜素新的区间的能力，但过大的交叉概率会使种群中的优良基因过早地破坏，从而使搜索过程趋于随机化而难以搜索到最优解；相反，会使搜索过程发展缓慢而陷于停滞，本文pc下限取0.6，上限取0.9。

变异概率pm控制着变异操作进行的频度，pm较大，可以产生较多的个体，但也会破坏很多较好的模式，使搜索陷入随机；相反，会限制新个体产生的能力而使算法容易陷入早熟，本文pm取0.1。

适应度函数为：

(9)

式中：n为可利用的观测数据个数；dmi为第i个控制测点的实测位移值；dci为第i个控制测点的有限元输出位移值。

最大进化代数取值100。

利用C++中drand函数在种群空间中投放随机数生成初始样本空间，初始种群中共含有50个个体，见表2。

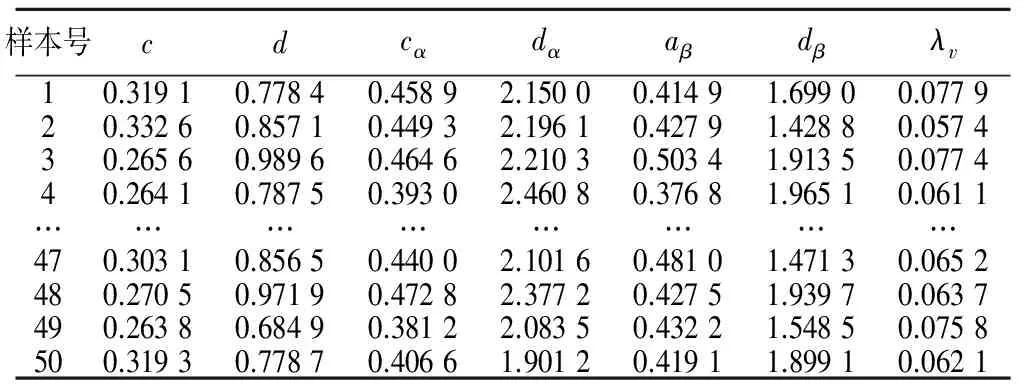
表2 50组参数的初始样本空间Tab.2 Initial sample space for fifty groups parameter

经流程图2，每一代种群适应度值随进化代数不断演化，共进化100代，见图7，由图7可以看出，种群染色体的平均适应值无限地接近最佳染色体适应值，说明最终染色体可信度不断提高，本文取第100代种群中的最佳染色体作为最终的反演参数，见表3。

图7 遗传算法进化过程Fig.7 Iteration process of GA

4 基于反演参数的大坝变形预测

采用反演的流变参数对水布垭大坝进行有限元正分析，图8给出了坝体部分目标监测点从2004-2020年的预测沉降历时图与近期实测沉降值的变化过程线，由图8可以看出，监测点的沉降预测计算值和实测值在数值和发展规律上均吻合度较好。图9～图10给出了2020年1月份的大坝位移变形预测计算结果, 此时大坝沉降为2.56m，占坝高的1.1%。

表3 基于遗传算法反演出的流变参数Tab.3 Results of parameter back analysis Based on GA

图8 坝体最大断面测点沉降实测值与反演值对比Fig.8 Comparison between measured and calculated settlements of points in the largest section of dam

图9 预测2020年大坝沉降图(单位：cm)Fig.9 Predicted settlements to 2020

图10 预测2020年大坝水平位移图(单位：cm)Fig.10 Predicted horizontal displacements to 2020

5 结 语

本文采用遗传算法和有限元正分析对流变参数进行了反演，并用反演所得参数，进行大坝长期变形计算，得出的主要结论如下。

(1)通过土工试验获取“真实”岩土工程参数存在着难以克服的误差，将自然界生物进化理论应用到工程上的遗传算法，可以解决大规模数值的进化。

(2)对流变参数较为敏感的7个参数进行了位移反分析，交叉概率和变异概率控制合理，克服了遗传进化过程陷入早熟收敛和局部最优，提高了反演效率。

(3)进行了基于反演参数的堆石坝应力应变分析。计算结果表明，大坝各测点全过程的计算沉降值与监测沉降值均吻合较好，且各特征时间点的沉降量均在合理范围之内，验证了计算参数和模型的有效性。

(4)通过长期反变形分析，得到了水布垭面板堆石坝2020年左右的大坝变形结果，此时大坝沉降为2.56 m，占坝高的1.1%，和同类工程比较沉降数值在合理范围内，整体变形符合一般规律。

□

[1] 孙 钧.岩土材料流变及其工程应用[M].北京:中国建筑工业出版社，1999.

[2] 周 伟，胡 颖.高混凝土面板堆石坝流变机理及长期变形预测[J].水利学报，2007，(10)：100-103.

[3] 程展林，丁红顺.清江水布垭面板坝填料蠕变试验研究[J].长江科学院，2003，(5).

[4] 沈珠江.堆石料的流变模型及其应用[J].水利水运科学研究，1994,(4)：335-342.

[5] Maranha das Neves E. Advances in Rockfill Structure[M]. London:Kluwer Academic Publishers,1991:89-91,221-236.

[6] Fitzpatrick M D,Liggins T B,Barnett R H W. Ten years surveillance of cethana dam[C]∥In:Proc.14th ICOLD Congress.Rio de Janeciro:[s.n.],1982:847-865.

[7] 周 伟. 高混凝土面板堆石坝流变本构模型理论及其应用[D].武汉：武汉大学，2004.

[8] 冯夏庭，杨成祥.智能岩石力学参数与模型的智能辨识[J].岩石力学与工程学报，1999.6，18(3):350-353.

[9] SL237-1999，土工试验规程[S].

[10] 卢声亮, 迟世春, 相 彪.复杂应力路径下邓肯-张EB模型适用性研究[J].城市勘测, 2009,(1):142-146.

[11] 孔宪京，张 宇，邹德高.高面板堆石坝面板应力分布特性及其规律[J].水利学报，2013，44(6)：631-639.