基于Copula函数的不同历时暴雨组合分析

万永静，朱程亮，刘 俊，李岱远

(1.河海大学水文水资源学院，南京 210098；2.南京水利科学研究院，南京 201129； 3.江苏省宿迁市水务局，江苏 宿迁 223800)

0 引 言

随着我国城市化进程的推进，城市内涝问题越来越受到社会和政府的关注。引起内涝灾害的主要因素是降雨强度超过排水标准，降雨历时和降雨范围超过区域排涝标准。城市的管道排水系统是按照市政排水规范设计，设计标准为2～5 a，设计历时采用不超过2 h的短历时为控制时段；城市区域排涝是按照水利部门的河道排涝规范设计，设计标准为10～30 a，设计历时采用3、6、24及72 h的长历时为控制时段[1-3]。由于两者设计历时及设计标准的差异，造成管道排水与河道排涝工程运行的不衔接，尤其是6、7月份连绵不断的长历时降雨极易导致排水管道受河道水位抬升带来的顶托作用，使得管道正常排水受到影响，引起城市内涝等灾害，对人们的生活生产造成一定的影响和损失。因此，将城市管道排水的短历时暴雨与河道排涝的长历时暴雨进行衔接，长历时暴雨与短历时暴雨关系进行遭遇组合分析，对解决这一现象有着很重要的意义。

Copula函数是被广泛用来构建联合分布的链接函数[4-6]，刘曾美等[7]采用Copula函数建立区间暴雨和外江洪水位的联合分布,用联合概率密度来描述两者遭遇的机率,用以分析排涝风险率和重现期；张娜等[8]利用 G-H Copula 函数构建年最大日雨量与年最大七日雨量之间的联合分布；陈子燊[9]等用Copula函数构建最大日降水量与历时7 d降水量两个组合的联合概率分布模式；谢华等[10]用Copula函数构建多变量联合概率模型，将其用于分析长江、淮河及黄河流域的径流量的联合概率和条件概率问题；陆桂华等[11]运用Copula函数构建了蚌埠市暴雨与淮河上游洪水遭遇概率模型。研究表明，Copula函数能够有效地描述水文事件的内在规律和特征属性之间的相互关系。

本文基于Copula函数，采用不同重现期下沭阳年最大2 h短历时管道排水暴雨(R2h)和其对应时段的最大1 d长历时区域排涝暴雨(R1d)为组合样本，建立联合分布概率模型，进行遭遇组合分析，计算超过某一设计值的短历时暴雨与超过某一设计值的长历时暴雨的同现重现期，计算在短历时暴雨不超过某一设计值的条件下长历时暴雨超过某一设计值条件重现期，研究结果可为城区排水防涝系统的建设提供科学依据，保障城区排水防涝安全。

1 研究方法

1.1 Copula函数

根据Sklar定理，随机变量X1、X2,…,Xd的联合分布F(x1,x2,…,xd)为：

F(x1,x2,…,xd)=P(X1≤x1,X2≤x2,…,Xd≤xd)=

C(u1,…,ud)

(1)

Copula函数能够通过边际分布和相关性结构两部分来构造多维联合分布，形式灵活多样，且求解比较简单。Copula函数的优势在于：边际分布可以采用任何形式。水文领域常用的几种Copula函数包括：Archimedean Copula函数、椭圆Copula函数以及经验Copu1a函数。其中，在水文分析方面以Archimedean Copula 函数应用为主。d维对称阿基米德copula 函数族定义为：

C(u1,…,ud)=φ-1[φ(u1)+φ(u2)+…+φ(ud)],

uk∈[0,1],k=1,…

(2)

式中：φ为Copula函数的生成函数；φ-1为φ的反函数。

水文中常用的二维Archimedean Copula函数有Clayton Copula、Frank Copula及GH Copula，其表达式见表1。

表1 常用的Archimedean Copula函数Tab.1 Common symmetric Archimedean Copula function

1.2 参数估计及拟合度检验

确定适宜的边际分布是应用 Copula 函数的第一步，Copula 函数不限定变量的边际分布类型。我国水文计算普遍采用的频率分布主要有皮尔逊Ⅲ型分布、指数分布和耿贝尔极值分布，理论频率曲线参数确定方法：先根据离差最小原则计算单历时样本系列的统计参数，再采用综合目估适线法对各历时暴雨统计参数进行调整，使其变化满足规律，最后选取拟合精度最高的分布函数计算变量的设计频率。

Copula 函数只含有一个计算参数θ，其可以根据Kendall秩相关系数τ和参数θ的关系(表1)计算，其中τ可以根据实测样本系列直接求得。

Copula函数拟合优度的检验方法主要选用离差平方和(OLS)最小准则法，OLS值越小表明拟合精度越高，选取OLS值最小的Copula 函数作为连接函数，OLS的计算公式为：

(3)

式中：Pei为经验概率；Pi为理论概率；i为数据系列序号。

1.3 概率及重现期

在组合概率及其重现期计算过程中，一般分析变量的同现概率、同现重现期、条件概率及条件重现期。

X1≥x1,X2≥x2同时发生的概率为：

P(X1≥x1∩X2≥x2)=1-u1-u2+C(u1,u2)

(4)

其重现期Ta为：

Ta=[1-u1-u2+C(u1,u2)]-1

(5)

在给定X1≤x1条件下，X2≥x2发生的概率为：

P(X2≥x2|X1≤x2)=1-C(u1,u2)/u1

(6)

其重现期Tc为：

Tc=u1/[1-C(u1,u2)]-1

(7)

2 不同历时暴雨组合分析

沭阳县地处江苏北部，沂沭泗水下游，属鲁南丘陵与江淮平原过渡带，幅员面积2 298 km2，以沭阳气象站1981-2015年共35 a的降水量数据为基本资料，选取沭阳县年最大2 h的短历时暴雨(R2h)和其对应时段的最大1 d长历时暴雨(R1d)为组合样本，进行联合分布概率分析。

2.1 边际分布函数参数计算

分别采用皮尔逊Ⅲ型分布、指数分布和耿贝尔分进行频率拟合计算，先根据离差最小原则计算单历时样本系列的统计参数，再采用综合目估适线法对各历时暴雨间统计参数进行调整，使其变化满足规律，确定频率分布参数，将3种频率分布曲线的频率计算的拟合离差进行比较。计算结果如表2所示。

表2 边际分布函数统计参数Tab.2 Statistical parameters of marginal distribution function

由表2可知，在进行短历时拟合时，拟合精度由高到低为耿贝尔分布、皮尔逊Ⅲ型分布和指数分布，其相对均方差分别为5.2%、6.4%和8.4%；在进行长历时拟合时，拟合精度由高到低为皮尔逊Ⅲ型分布、耿贝尔分布和指数分布，其相对均方差分别为6.1%、7.1%和8.8%。依拟合指标而言，短历时拟合精度最高的为耿贝尔分布，长历时拟合精度最高的为皮尔逊Ⅲ型分布。设长历时暴雨相对均方差与短历时暴雨相对均方差的算数平均值为综合误差，皮尔逊Ⅲ型分布拟合的综合误差为6.25%，耿贝尔分布拟合的综合误差为6.15%，鉴于皮尔逊Ⅲ型分布拟合和耿贝尔分布拟合的综合误差接近，本次采用水文计算中习惯用的皮尔逊Ⅲ型分布计算设计暴雨概率，绘制边际分布概率图(图1)。

图1 边际分布概率Fig.1 Marginal probability distribution

2.2 Copula函数参数计算

根据实测资求得各个组合的Kendall秩相关系数τ，由τ和Copula函数参数θ的关系(表1)可以求得θ。由表3可知秩相关系数τ为0.421，即长历时暴雨和短历时暴雨的成正相关，故可以用Archimedean Copula函数进行联合分布计算。根据式(3)，采用OLS法检验函数的拟合优度，OLS值越小表明拟合精度越高，选取拟合度最好的函数，相关计算参数见表3。

表3 R2h和R1d的相关计算参数Tab.3 Several calculation parameters of R2h and R1d

由表3可知，Frank Copula函数的OLS值最小，表明其拟合效果最佳，故采用Frank Copula函数进行联合分布计算，将长历时暴雨和短历时暴雨的经验累积概率和采用Frank Copula函数计算理论累积经验概率绘制在一张图上，如图2所示。

图2 R2h和R1d的经验累积概率和理论累积概率比较Fig.2 Comparison of empirical and theoretical accumulation probabilities

由图2可以看出，联合经验累积概率和联合理论累积概率的点距基本形成一条45°的对角线，表明联合经验累积概率和联合理论累积概率计算结果接近，采用Frank Copula函数计算长历时暴雨和短历时暴雨的联合分布概率合理。

2.3 联合分布计算

由表2中的边际分布参数可以求得长历时暴雨与短历时暴雨所对应的边际分布概率，由表3可以得到Copula函数的统计参数，根据拟合结果选取Frank Copula函数为联合分布函数，由Copula函数关系式及其对应的参数θ，计算联合分布概率，绘制联合分布概率图(图3)，从图中可以查出任意量级的长历时暴雨与短历时暴雨组合的联合分布概率。

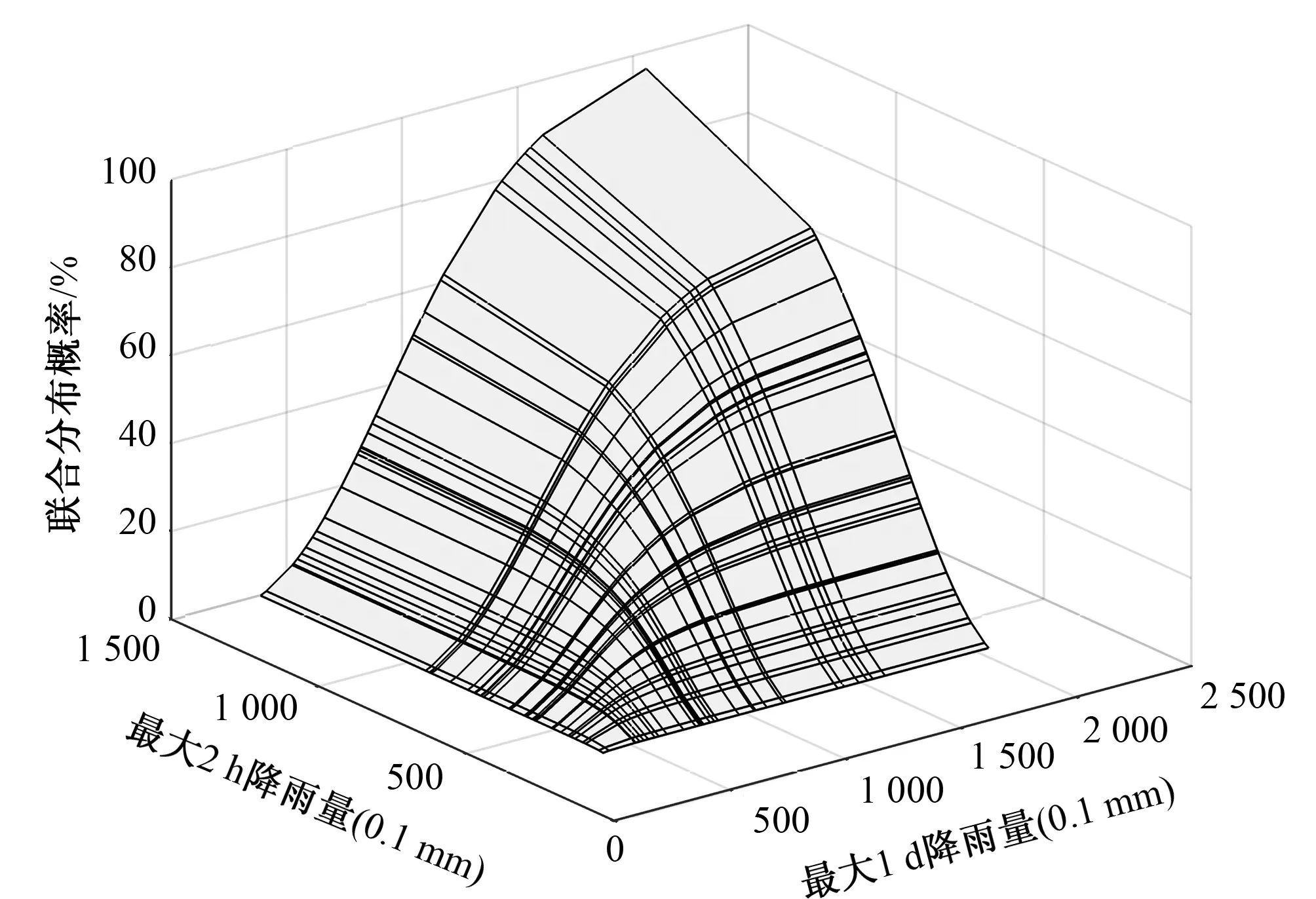
图3 联合分布图Fig.3 Joint probability distributions

2.4 组合重现期分析

由于城市的管道排水系统和区域排涝系统两者设计历时及设计标准存在差异，会造成管道排水与河道排涝工程运行不衔接，将2 h的短历时暴雨和1 d的长历时暴雨进行组合分析。当短历时暴雨和长历时暴雨同时发生时，河道排涝水位是上涨，管道排水可能受河道排涝水位顶托影响，城市排涝压力增大。根据式(4)～式(7)，主要分析了短历时暴雨和长历时暴雨均超过某一量级的同现重现期，及短历时暴雨在发生小于某一量级的暴雨时，长历时暴雨发生大于某一量级的暴雨的重现期(表4)。

表4 组合重现期分析Tab. 4 Combined Reproductive Period Analysis

由表4可以看出，2 a一遇的短历时暴雨和20 a一遇和30 a一遇的长历时暴雨同现重现期分别为24.8、37、3 a一遇的短历时暴雨和20 a一遇和30 a一遇的长历时暴雨同现地重现期分别为32.1、47.6 a。在发生小于2 a一遇的短历时设计暴雨时，发生超过20 a一遇和30 a一遇的长历时暴雨条件重现期分别为12.4和18.5 a，在发生小于3 a一遇的短历时暴雨时，发生超过20 a一遇和30 a一遇的长历时暴雨条件重现期分别为10.7和15.9 a。可以看出同现重现期大于任何一个单一变量的重现期，条件重现期介于两个单变量重现期之间。在排水防涝系统建设过程中，根据区域长历时短历时降雨特性，采用不同的组合重现期进行分析，为排水防涝系统设计提供科学依据，保障城市排水防涝安全。

3 结 语

基于沭阳县1981-2015年35 a的降雨数据，将2 h的短历时暴雨和1 d的长历时暴雨进行组合分析，主要得出以下结论。

(1)分别采用皮尔逊Ⅲ型分布、指数分布和耿贝尔分布进行频率计算拟合，结果表明，短历时拟合精度最高的为耿贝尔分布，长历时拟合精度最高的为皮尔逊Ⅲ型分布，但皮尔逊Ⅲ型分布和耿贝尔分布的综合拟合精度接近，本次计算采用水文计算中习惯用的皮尔逊Ⅲ型分布。

(2)采用水文中常用Clayton Copula、Frank Copula及GH Copula函数构建联合分布计算模型，采用OLS法进行联合经验累积概率和联合理论累积概率拟合精度检验，结果表明Clayton Copula函数拟合精度最好。

(3)将短历时重现期和长历时重现期进行联合分布计算，分析组合同现重现期和条件重现期，计算结果表明短历时暴雨重现期2～5 a与长历时暴雨重现期10～30 a的同现重现期为12.5～259.3 a，条件重现期为4.6～18.5 a。在排水防涝系统建设过程中，根据联合设计标准及区域长历时短历时降雨特性，采用不同的组合重现期进行分析，将管道排水与区域排涝统筹考虑，可以更好地确定工程的规模大小，为排水防涝系统建设提供科学依据，保障城市排水防涝安全。

□

[1] 于凤存,王友贞,蒋尚明,等. 基于设计暴雨强度城市河道排涝与管渠排水标准关系研究[J]. 灾害学,2015,(1):21-24.

[2] 黄建文. 南昌市管道排水与河道排涝设计标准衔接研究[D]. 南昌：南昌大学,2012.

[3] 车 伍,杨 正,赵 杨,等. 城市排水(雨水)防涝综合规划编制若干问题探讨[J]. 中国给水排水,2014,(16):6-11.

[4] Zhang L, Singh V P. Bivariate flood frequency analysis using the copula method [J]. Journal of Hydrologic Engineering, 2006,11(2):150-164.

[5] 郭生练,闫宝伟,肖 义,等. Copula函数在多变量水文分析计算中的应用及研究进展[J]. 水文,2008,(3):1-7.

[6] 宋松柏, 蔡焕杰, 金菊良,等. Copula函数及其在水文中的应用[M]. 北京:科学出版社, 2012:87-89.

[7] 刘曾美,陈 子. 区间暴雨和外江洪水位遭遇组合的风险[J]. 水科学进展,2009,(5):619-625.

[8] 张 娜,郭生练,肖 义,等. 基于联合分布的设计暴雨方法[J]. 水力发电,2008,(1):18-21.

[9] 陈子燊,刘曾美. 不同历时设计暴雨组合的风险率分析[J]. 水文,2011,(4):12-17.

[10] 谢 华,罗 强,黄介生. 基于三维copula函数的多水文区丰枯遭遇分析[J]. 水科学进展,2012,(2):186-193.

[11] 陆桂华,张亚洲,肖 恒,等. 气候变化背景下蚌埠市暴雨与淮河上游洪水遭遇概率分析[J]. 气候变化研究进展,2015,(1):31-37.