考虑水轮机特性项的尾水调压室临界稳定断面公式研究

2017-03-23李路明李高会

中国农村水利水电 2017年11期

关键词：尾水传递函数水轮机

杨飞，李路明，李高会

(中国电建集团华东勘测设计研究院有限公司，杭州 311100)

0 引言

调压室稳定断面的确定对于电站的稳定运行具有至关重要的作用。1910年，Thomas通过简化数学模型[1]，给出了最早的调压室稳定断面公式：

(1)

该公式的推导建立在理想水轮机和理想调速器的方程下，并假定调压室与压力引水道联通点的下游一端的水头与流量之积为常数；随后，Garden、Evangelisti等[1]对该公式进行了进一步的研究，并给出了包含水轮机效率项的调压室稳定断面公式，但二者给出的公式中效率项均为微分形式，求解过程较为复杂；杨建东等[2]进一步研究了水轮机特性等因素对于调压室临界稳定断面的影响，但其计算仍需对水轮机综合特性曲线进行插值等计算，过程较为烦琐。由此可见，以上学者均未给出可以直接用于计算水轮机特性影响的调压室稳定断面表达公式，而水轮机特性对于调压室稳定断面的影响不可忽略。因此，本文将结合调压室及水道局部模型、发电机及负荷局部模型、调速器局部模型等，利用传递函数[3]的思想，力求推导出一个可以直接用于计算水轮机特性影响的尾水调压室稳定断面表达公式，并进一步探讨水轮机特性对于尾水调压室稳定断面的影响。

1 公式推导

1.1 尾水调压室及水道局部模型

包括尾水调压室在内的水道基本方程分别为调压室连续方程、压力尾水道水流运动方程和压力管道水流运动方程：

Tgzs=qP-qT

(2)

TwqTs=z-k1qT

(3)

h=-z-TeqPs-k2qp

(4)

联合式(2)、式(3)、式(4)并消去变量z和qT得：

(5)

研究表明，压力管道水流加速时间常数Te对调压室稳定断面影响极小，完全可忽略。因此，式(5)可简化为：

(6)

1.2 水轮机局部模型

根据水轮机出力、单位流量与单位转速方程不难得出水轮机局部模型：

(7)

1.3 理想孤网条件下发电机及负载局部模型

发电机组转动部分运动方程、水轮机做功方程和负荷阻力矩方程分别为：

(8)

求解上述方程组，得出机组转速对水轮机出力的传递函数在不计发电机损耗的情况下为：

(9)

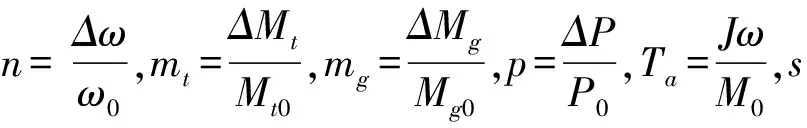
1.4 调速器局部模型

当不考虑调速器中的加速度环节和忽略液压放大系统中的对计算结果影响较小的时间常数时，PI型软反馈调速器方程可简化为：

(10)

式中：y为接力器行程或导叶开度相对值；nref为转速给定相对值；bp为调速器的永态转差系数；bt为暂态转差系数；Td为缓冲时间常数。

对式(10)进行拉普拉斯变换可得其传递函数表达式为：

(11)

1.5 系统整体模型

1.5.1 带调压室的水轮发电机组开环传递函数

将式(6)、式(7)和式(9)联立：

(12)

应用刚性水击理论，可以认为压力管道流量与水轮机流量相等，即qp=q。整理上面的联立方程组，消去h、q、p后可得到带调压室的水轮发电机组的开环传递函数为：

(13)

式中：b2=TgTwQy[(1+eq)-k2(1+eh)]；b1=k1TgQy[(1+eq)-k2(1+eh)]-TwQy(1+eh)；b0=Qy(1+eq)-Qy(k1+k2)(1+eh)；a3=(1+0.5k2)TgTwTa；a2=k1TgTa(1+0.5k2)+0.5TwTa；a1=(1+0.5k1+0.5k2)Ta；a0=0。

1.5.2 带调压室的水轮机调节系统闭环传递函数

为推导方便计，令b′t=bt+bp, 式(11)可写为：

(14)

根据单位反馈系统闭环传递函数计算公式，带调压室的水轮机调节系统闭环传递函数为：

(15)

式中：B3=[1-k2δ]TdTgTwQy；B2=k1(1-k2δ)TgTdQy-δTwTdQy+(1-k2δ)TwTgQy；B1=[1-(k1+k2)δ]TdQy+k1(1-k2δ)TgQy-δTwQy；B0=Qy[1-(k1+k2)δ]；C4=γ(1+0.5k2)TgTwTab′tTd；C3=[1-k2δ]TdTgTwQy+k1(1+0.5k2)γb′tTgTaTd+0.5γb′tTwTaTd+(1+0.5k2)γbpTgTaTw；C2=k2[1-k2δ]TgTdQy-δTwTdQy+(1+0.5k1+0.5k2)γb′tTaTd+[1-k2δ]TwTgQy+k1(1+0.5k2)λbpTgTa+0.5γbpTwTa；C1=[1-(k1+k2)δ]TdQy+k1[1-k2δ]TgQy-δTwQy+(1+0.5k1+0.5k2)γbpTa；C0=Qy[1-(k1+k2)δ]。

1.6 包含水轮机效率的调压室稳定断面公式

式(15)就是本文建立的在理想孤网运行条件下用于作调压室小波动稳定分析的整体数学模型。这个模型用传递函数表达，是一个4阶动态模型。一个闭环系统传递函数的分母即为该系统的特征多项式，因此该系统的特征方程为：

C4s4+C3s3+C4s4+C1s+C0=0

(16)

如果假定调速器为理想调速器，即可令b′t=0，bp=0，Td=0，系统的特征方程式由四次变为二次：

C2s2+C1s+C0=0

(17)

式中：C0=Qy[1-(k1+k2)δ]；C1=k1(1-k2δ)TgQy-δTwQy；C2=(1-k2δ)TeTgQy。根据Routh-Hurwiz稳定判据，对于一个二阶系统，系统稳定应满足的充分必要条件是特征多项式的三个系数均大于零，即C0>0，C1>0，C2>0 。通过对本文中定义的无量纲参数k1,k2的分析我们知道，在一般的水电站中它们的值都远小于1。而相关分析表明δ是一个1.0到1.3左右的值，因此C0>0和C2>0这两个条件的满足是不成问题的。因此，系统的稳定只要满足C1>0 即可。而该系统稳定的临界条件为C1=0，即：

k1(1-k2δ)Tg-δTw=0

(18)

根据前文中对k2、k3的定义，上式可整理为：

(19)

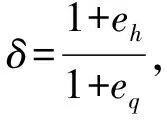
式(19)就是本文得到的目前较为完整的考虑水轮机特性的尾水调压室临界稳定断面公式。比较式(19)与规范中的尾水调压室临街稳定断面公式[4]：

(20)

可以看出，当不考虑水轮机特性的影响时，水轮机特性相关项δ=1，式(19)与规范公式(20)一致。

1.7 关于公式中δ参数的讨论

由δ的定义可以看出，δ值可以根据实际的水轮机特性曲线通过数值差分进行求解，而反映水轮机特性的数据往往来自模型试验数据，模型试验数据是离散的，因此，通过数值差分计算的δ值结果的准确性较差。研究表明，δ值与水轮机的比转速存在一定的相关性。1994年Norconsult用数理统计方法来找其中的相关性，并给出了δ的经验计算公式：

δ=0.000 9ns+1.044

(21)

由此，式(19)可直接用于计算考虑水轮机特性影响下的尾水调压室稳定断面积。需要注意的是，式(21)中的δ值是在额定净水头下接近满开度运行时δ的经验公式，因此在实际应用中存在一定的近似。

2 算例分析

为了对进一步说明式(19)中水轮机特性项对于尾水调压室稳定断面的影响，选取国外某低水头电站为例，分别采用规范公式(20)与本文推导的式(19)计算3种典型工况下的临界稳定断面，并对计算结果进行分析。电站基本资料如下：电站共6台机，单机容量102 MW，引水单洞单机，尾水三机一洞共用一尾水调压室。额定水头60 m，上游正常蓄水位1 030.00 m，上游死水位1 028.00 m，下游六台机发电水位961.23 m，实测历史最高洪水位963.3 m。压力尾水道长8 672.5 m，压力尾水道断面积141.56 m2，单机引用流量182.1 m3/s，压力尾水道流速3.86 m/s，压力尾水道水头损失6.6 m，压力管道水头损失1.12 m，尾水管延伸段水头损失1.18 m。采用规范公式(20)与本文推导公式(19)计算的尾水调压室结果如表1所示。

表1 本文公式与规范公式临界稳定断面计算结果Tab.1 Critical stable area of the tailrace surge chamber caculatedby stanfard formula (20) and (19) derived in this paper

注：均用额定流量算便于比较。由于水头差异，在同一流量下，开度与出力都不相同。

比较表1中规范公式与本文公式计算结果可以看出，对于本电站目前所采用的尾水调压室断面，采用规范公式计算的安全系数均大于1，即在三种工况下，调压室均是稳定的；而采用本文公式的计算结果表明，三种典型工况下尾水调压室安全系数均小于1，即考虑了水轮机特性之后，尾水调压室不稳定。由此可以看出，在这三种工况下，水轮机特性对调压室稳定是不利的。为了进一步确定三种工况下调压室的稳定性，采用数值计算的方法对三种工况进行小波动分析，小波动工况如下。

工况1：1号机、2号机、3号机初始出力分别为:102，104, 104 MW；初始净水头分别为：58.95，58.8，58.8 m；负荷扰动后出力：104，104，104 MW；扰动后导叶开度中间值： (约) 0.93，0.93， 0.93。

工况2：1号机、2号机、3号机初始出力分别为:98，100，100 MW；初始净水头分别为：57.4，57.2，57.2 m；负荷扰动后出力:100，100, 100 MW；扰动后导叶开度中间值:(约)0.94，0.94，0.94 。

工况3：初始出力: 1号机：90 MW ，2号、3号机92 MW；初始开度: 0.86 ，0.88，0.88；初始净水头: 56.6， 56.4，56.4 m；负荷扰动后出力: 92，92，92 MW；扰动后导叶开度中间值:(约) 0.89，0.89，0.89。

对以上3种工况进行数值模拟，调压室水位波动计算结果如图1～图3所示。

图1 实际断面工况1尾水调压室水位波动过程线Fig.1 Water level fluctuation hydrograph of the tailrace surge chamber in condition 1

图2 实际断面工况2尾水调压室水位波动过程线Fig.2 Water level fluctuation hydrograph of the tailrace surge chamber in condition 2

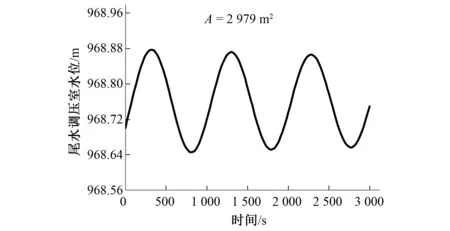
图3 实际断面工况3尾水调压室水位波动过程线Fig.3 Water level fluctuation hydrograph of the tailrace surge chamber in condition 3

分析：图1、2、3分别为尾水调压室断面取实际断面2 979 m2时，工况1～3的调压室水位波动过程，分析这3幅图可以看出，工况1、2的尾水调压室水位波动呈现扩散的现象，即在工况1、2下尾水调压室的实际安全系数小于1；工况3的尾水调压室水位波动衰减微弱，说明此工况下调压室实际安全系数接近1，调压室几乎处于临界状态。当调压室断面按照本文公式的计算取值时，工况1～3的调压室水位波动过程如图4～图6。由图4～图6可以看出，当尾水调压室断面按照本文推倒的公式取值时，工况1～3下的调压室水位波动均呈现收敛的趋势，即当采用本文公式计算的调压室稳定断面值时，调压室小波动稳定。以上数值分析结果表明，表1中采用本文公式的稳定断面与实际更为一致，安全性更高。而分析以上结果产生的原因，必须将水轮机特性系数δ考虑进来。相关分析结果表明[2]，δ值与水轮机开度有关，开度越大，δ值越大，对调压室的稳定断面要求越高。由此，本文根据实际的水轮机特性曲线，给出了额定水头(60 m)下δ及其他有关参数与导叶开度的函数关系。

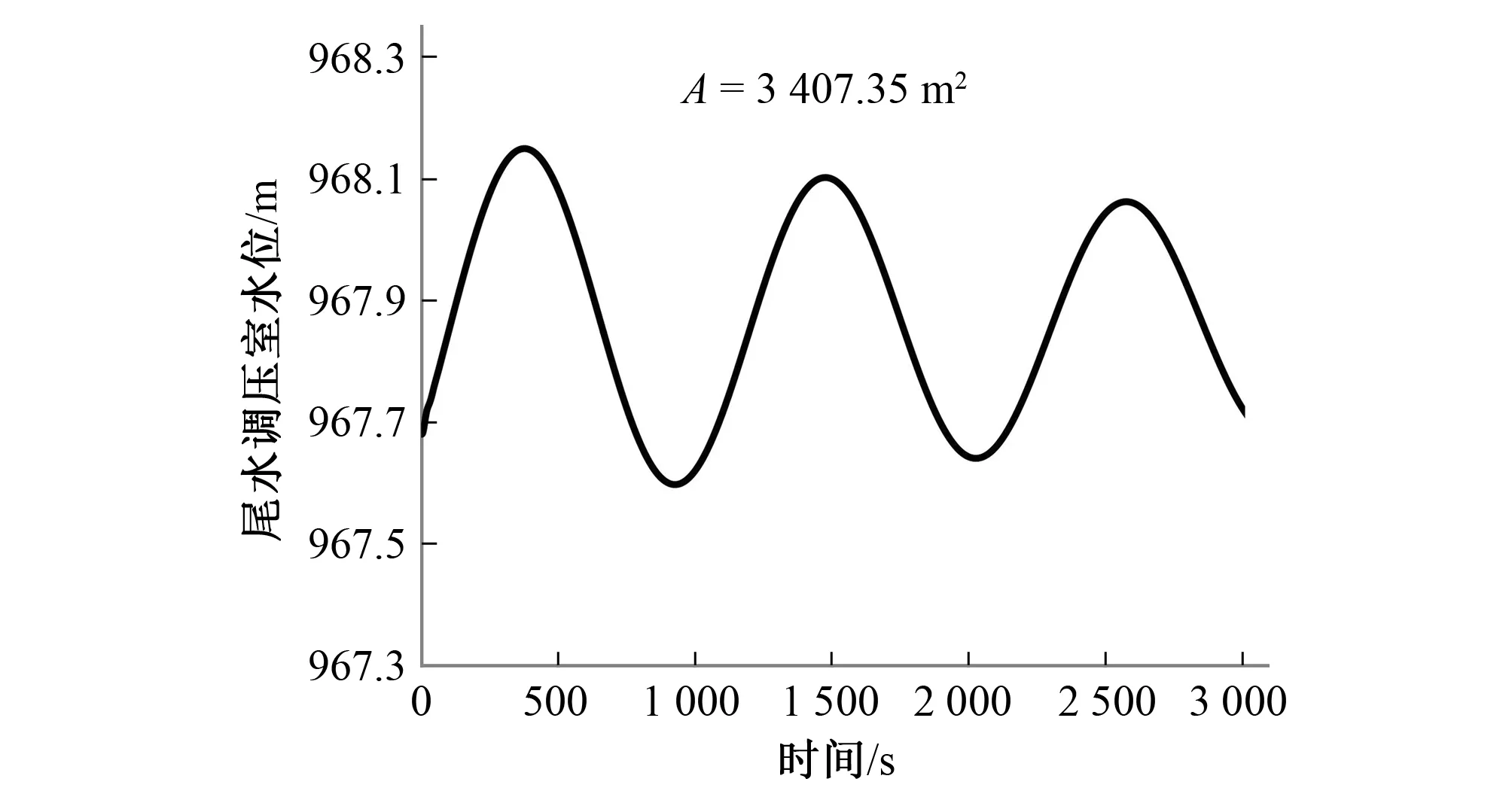
图4 计算值断面工况1尾水调压室水位波动过程线Fig.4 Water level fluctuation hydrograph of the tailrace surge chamber in condition 1

图5 计算值断面工况2尾水调压室水位波动过程线Fig.5 Water level fluctuation hydrograph of the tailrace surge chamber in condition 2

图6 计算值断面工况3尾水调压室水位波动过程线Fig.6 Water level fluctuation hydrograph of the tailrace surge chamber in condition 6

根据工况1、2、3扰动后的机组开度值对照表2通过插值方法可以计算出3种工况下的水轮机特性系数δ分别为1.15、1.2、1.03。其中工况1、2下的水轮机特性系数δ较最低水头工况3的δ大很多，即水轮机特性对工况1、2下尾水调压室的负面作用远大于工况3，且这种影响已经超过净水头对于稳定断面的影响，从而导致工况1、2下的尾水调压室均是不稳的，且最低水头工况3的安全系数超过工况1、2，最不利工况已从最小水头工况3转移。由此可以看出，水轮机特性对于尾水调压室稳定断面影响显著，考虑水轮机特性的尾水调压室稳定断面公式(19)安全性更高。需要说明的是，本文的都是基于孤网的分析，考虑到实际的电网特征，对于实际调压室断面小于公式(19)计算结果的调压室亦可能是稳定的，具体须结合实际电网进行数值分析验证。