单级离心泵叶轮在干式状态下的模态分析及试验研究

王学谦，黄 思，张雪娇，邱光琦

(华南理工大学机械与汽车工程学院，广州 510640)

0 引 言

随着离心泵工作范围的扩大，现代工程技术对其各方面的性能要求也愈来愈高，不仅要求具有较高的效率和较强的变工况适应性，更要求其在结构上具有紧凑性、高可靠性和稳定性。实际工作中，高速运转的离心泵在外界激振力的影响下会产生振动，为避免共振和结构破坏等不良后果的产生，在离心泵设计时需要考虑转子系统的结构特性和振动特性。

模态分析是研究结构振动的常用方法之一，用于确定结构或机器部件的振动固有特性(固有频率和振型)，是后期结构改进的基础[1,2]。国内外许多学者从有限元仿真和模态试验两方面对叶轮模态分析做了大量工作[3-7]，得到其振动模态参数，为分析振动引起的叶轮、叶片损坏故障提供了参考依据[8,9]。仿真模态分析和试验模态分析各有不足，仿真模态分析计算烦琐、耗资费时，有些参数(如阻尼、结合面特征等)尚无法定值，使得计算结果是一个近似值。而试验模态分析往往在具体应用时存在局限性。

本文有机地结合了仿真模态分析和试验模态分析方法的优点，采用Pro/E软件对该叶轮结构进行三维建模，利用ANSYS Workbench协同仿真平台、德国BBM测试分析系统和LMS Test.lab模态分析软件对离心泵叶轮进行自由状态下的仿真模态计算和模态测试，得到各阶的模态参数，为离心泵叶轮设计提供参考，避免叶轮的固有频率和激振力频率相同或相近产生共振现象，从而保证离心泵的正常运行。

1 离心泵叶轮仿真模态分析

模态分析实质上是一种坐标变换，其目的在于把原物理坐标系中描述的相应向量转换到“模态坐标系统”中来描述，为结构系统的振动特性分析、振动故障诊断、预报以及结构动力特性的优化设计提供依据。其固有频率、阻尼比和模态振型等模态参数可以通过理论计算或试验分析获得[10-12]。

1.1 仿真模态分析基础

仿真模态分析是一种理论建模过程，主要运用有限元方法对振动结构进行离散，建立系统特征值的数学模型，用各种近似方法求解系统特征值和特征矢量，由于对阻尼难以准确的处理，对于一些小阻尼系统的阻尼通常忽略不计[13]。

在动力学问题中，自由度为n的线性结构系统的运动微分方程为：

(1)

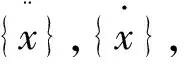
本文离心泵叶轮的自振频率是在不考虑阻尼情况下的自由振动，即[C]=0，{F(t)}=0。设式(1)的特解为简谐函数形式：

{u}={φ} sin(ωt+α)

(2)

式中：{φ}为特征向量或整型；ω为圆频率；α为相位角。将式(2)代入式(1)，得到方程组：

([K]-ω2[M]){φ}={0}

(3)

在式(3)中，[K]-ω2[M]为系统的特征矩阵，由于自由振动中各点的振幅不全为零，因此必须满足：

(4)

将式(4)展开，可得出ω2的n次代数方程式：

ω2n+a1ω2(n-1)+…+an-1ω2+an=0

(5)

式(5)为结构系统的特征方程。因此，求解系统的固有频率便是求解特征方程式(5)的特征值ωi。将ωi代回式(3)，可得到与之对应的特征向量{φ}i，特征向量{φ}i描述了结构系统在第i阶固有频率ωi下的固有振型。

第i个特征值与第i个固有频率间的关系如下式：

fi=ωi/2π

(6)

式中：fi为第i个固有频率。

1.2 叶轮的仿真模态计算

本文主要借助ANSYS Workbench协同仿真平台来对离心泵进行自由状态下的模态仿真，过程如下：首先通过Pro/E 5.0建立叶轮固体的三维模型，然后采用ANSYS Workbench自带的网格划分模块对其进行网格划分，最后在ANSYS Workbench平台下的Modal模块进行模态的求解。

1.2.1 叶轮固体模型的建立及网格划分

本文选用材料为HT200、干式状态下XA100/32型单级离心泵叶轮为研究对象，其材料特性如表1所示。

表1 叶轮材料特性Tab.1 Material characteristics of impeller

图1为离心泵叶轮实体模型，在进行网格划分时，离心泵叶轮结构模型较为复杂，故选用系统自带并且适应性好的自动划分网格法，即利用Pro/E与ANSYS Workbench的接口将叶轮造型导入软件中，插入自动划分网格的方法。最终生成的叶轮实体总网格数为125 234，节点数为222 502。叶轮网格划分的结果如图2所示。

图1 叶轮实体三维模型Fig.1 3D model of impeller solid

图2 叶轮实体网格划分图Fig.2 Mesh diagram of impeller solid

1.2.2 仿真计算结果分析

仿真计算采用ANSYS Workbench协同仿真平台中的Modal模块求解叶轮在自由状态下的模态，叶轮的前六阶固有频率和最大振幅值如表2所示，叶轮前六阶的振型如图3所示。

表2 叶轮的仿真模态结果Tab.2 Simulation modal results of impeller

图3 叶轮前六阶振型图Fig.3 The first six vibration modes of impeller

结合表2和图3可以发现叶轮的一、二阶在两个正交方向上存在同频率的两振型，即模态重频，叶轮五、六阶模态亦此，这主要是由于叶轮结构为中心对称分布，使得叶轮的模态结果呈现出振型和频率相同但相位不同的振动现象。叶轮的一阶和二阶振型为两根节径的振动，在叶片进口处变形量达到最大；三、四阶模态的固有频率值也基本相近，三阶振型为三根节径的伞形振动，且变形量呈中心对称分布且叶轮的变形随半径增大而增大，最大变形发生在叶片出口处；四阶振型为三根节径的振动，在叶片进口处和叶片出口处变形量达到最大；五阶和六阶振型重频，均为两根节径的振动，最大变形发生在叶片出口处。

2 离心泵叶轮模态试验

2.1 试验设备及方法

试验模态分析是通过检测与控制仪器对系统运行过程中呈现出来的响应信号和激励信号进行测量，以此求解出振动特性的频响函数，最后利用参数识别的方式得到系统的模态参数和物理参数。本试验对离心泵叶轮进行了自由状态下的模态测试试验，在力锤的激励下使叶轮结构产生响应，从而求得随频率变化的传递函数，试验原理如图4所示。

图4 模态分析试验原理Fig.4 Modal analysis test principle

本试验采用的试验仪器及设备如表3所示。试验中用橡皮绳悬吊叶轮，并通过滑轮调整叶轮位置，使其尽量处于水平状态。然后将三向加速度传感器分别安装在叶轮前盖板、叶片和后盖板的非对称的响应点处，如图5所示。并在叶轮上用记号笔标出了30个测点的位置，采用PCB力锤分别敲击叶轮的30个测点使其产生结构响应，然后经 PCB压电式三向加速度传感器测试出每个测点的响应信号被德国BBM测试设备(如图6)的MK II信号采集器采集和PAK测试分析系统导出传递函数，最后采用LMS Test.lab软件进行模态分析和处理，得到叶轮的模态参数。

图5 传感器位置布置图Fig.5 Diagram of sensor location layout

图6 德国BBM数据采集分析系统Fig.6 Germany BBM data acquisition and analysis system

2.2 模态测试信号处理

采用最小二乘复频域法(Ploy MAX)对模态测试系统采集到的频响函数信号进行数据分析并提取模态参数，图7为采用Ploy MAX法对频响函数进行分析得到的结果稳态图。其中横坐标为频率，纵坐标为幅值，模态指示函数的尖峰位置为模态的真实位置，每个尖峰位置所对应的横坐标为各阶模态的固有频率。

图7 Ploy MAX法频响函数分析结果稳态图Fig.7 Ploy MAX method of frequency response function analysis results steady state diagram

2.3 模态测试试验结果分析

离心泵叶轮的试验模态分析与仿真模态分析的结果对比如表4所示。从表4可知，仿真计算结果和试验得出的固有频率误差值基本在10%以内，从而验证了模拟仿真结果的正确性，为之后的模拟计算提供了相应基础。由于在实际试验操作过程中存在非线性的阻尼特性，但在ANSYS模态分析计算中忽略阻尼作用，所以这些原因产生了一定的误差。总的来看，虽然有限元分析的结果和试验结果有误差，但大体趋势一致，有较好的对应关系。

表4 离心泵叶轮的模态分析试验与仿真结果对比Tab.4 The comparison of modal analysis and simulationresults of centrifugal pump impeller

3 结 语

本文结合仿真模态分析及模态试验的方法，研究了离心泵叶轮的振动特性，根据其固有频率和振型分布得出以下结论。

(1)叶轮结构为中心对称分布，使得叶轮的模态结果成对呈现出振型和频率相同但相位不同的振动现象。

(2)仿真结果与试验频率的误差基本在10%以内，验证了仿真模态分析的有效性，为后续的转子系统的仿真模态分析提供了计算依据。

(3)有机地结合仿真模态分析和试验模态分析方法，取长补短。利用试验模态分析结果检验、补充和修正原始有限元动力模型，修正后的有限元模型计算结构的动力特性和响应为离心泵结构优化设计提供参考。

□

[1] 树 谦, 文 德, 物理工程, 等. 振动结构模态分析: 理论, 实验与应用[M]. 天津：天津大学出版社, 2001.

[2] 梁 君, 赵登峰. 模态分析方法综述[J]. 现代制造工程, 2006,(8):139-141.

[3] Subramaniam L, Sendilvelan S. Modal analysis of a centrifugal pump impeller[J]. European Journal of Scientific Research, 2012,79(1):5-14.

[4] Rad S Z. Finite element, modal testing and modal analysis of a radial flow impeller[J]. Iranian Journal of Science & Technology, Transaction B, Engineering, 2005,29(B2).

[5] Luo T S, Dai R. Modal analysis of integrated radial inflow impeller with finite element method[J]. NeiranjiGongcheng(Chin. Intern. Combust. Engine Eng.), 2005,26(1):77-80.

[6] 徐建国. 轴流泵叶片应力与模态分析[D]. 江苏扬州: 扬州大学, 2008.

[7] 石永强, 王维民, 宁 喜, 等. 离心压缩机叶轮振动特性仿真及试验研究[J]. 风机技术, 2012,(5):27-30.

[8] 司乔瑞, 余志顺, 袁寿其, 等. 带诱导轮高速离心泵流动诱导振动数值分析[J]. 振动与冲击, 2013,32(20):102-106.

[9] 陈立明. 汽轮机叶片—轮盘耦合振动分析[D]. 北京：北京工业大学, 2005.

[10] Larsen G C, Hansen M H, Baumgart A, et al. Modal analysis of wind turbine blades[R]. 2002.

[11] Deines K, Marinone T, Schultz R, et al. Modal analysis and SHM investigation of CX-100 wind turbine blade[M]. Rotating Machinery, Structural Health Monitoring, Shock and Vibration, Volume 5. Springer New York, 2011:413-438.

[12] Wang B T, Cheng D K. Modal analysis of mdof system by using free vibration response data only[J]. Journal of Sound and Vibration, 2008,311(3):737-755.

[13] 黄 思. 流体机械数值仿真研究及应用[M]. 广州:华南理工大学出版社, 2015.