基于GARCH—VaR模型对沪深300ETF基金的实证分析

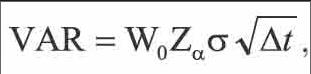
【摘要】由于在金融领域内，GARCH模型在金融时间序列波动率的模拟以及金融风险的度量中都有着相对广泛的应用。故而本文基于GARCH模型以正态分布的假定度量VaR值的精确程度，并且对VaR值进行失败率检测。结果表明，沪深300ETF基金具有尖峰厚尾特特征；利用EViews8.0对基金收益率序列进行相关性检验，发现其具有强相关性。通过GARCH模型消除相关性，对收益率建模，有效预测估计了基金的VaR值。

【关键词】沪深300ET基金 Eviews8.0 GARCH-VaR 自相关VaR回测检验

一、引言

对于指数的研究，只能通过对跟踪其指数的ETF（Exchange Trade Fund）基金走势的计量进行观测。当前市场上跟踪沪深300指数的基金有很多，但国内学者通常使用的嘉实沪深300ETF。ETF基金是基金托管人通过“复制”和追踪指数的变化来运作的，换句话说，实际上ETF基金是由一揽子股票组成的投资基金，托管人会尽可能地使ETF基金指数与净值同步。但是沪深300ETF基金作为指数基金中的一种，本身虽然有许多优点，然而相对来说还是具有很大的局限性。近年来，众多学者对于指数基金的研究已经不胜枚举，但对沪深300ETF基金的研究相对来说并不算多。而在近来股市牛熊转变的过程中，ETF基金的市场风险日益扩大。所以，在后金融危机时代，如何加强对基金的风险管理已经成为基金管理者的一个重大课题。VaR方法能表示各类风险，并提供发生概率，所以成为当前风险管理方面最通用的一种方法。

因此，本文选取沪深300ETF基金数据，基于GARCH模型精确的计算VaR值，从波动性的角度，建立GARCH族模型，并且相互比较，计算出VaR值，分析VaR值与实际收益率的差别。再利用金融时间序列本身尖峰厚尾的特征来跟踪收益率变动方差的方法，为基金管理者评估，度量与防范金融风险提供一定的决策参考，希望的到研究者的重视。

二、理论基础

（一）理论基础

风险价值度（Value at risk，VaR）企图对金融机构的资产组合提供一个单一的风险度量，而这一度量正好可以体现金融机构的整体风险。

VAR的定义是在一定的持有期内和一定的置信水平下投资者或机构预期下的最大损失。其数学公式为 ，其中Δp为证券组合在持有期t内的损失，C表示给定的置信水平，VaR表示置信水平C下处于风险中的价值。

但在实际生活中，大家经常使用德尔塔——正态分布法[1]，其公式为 ，其中W0表示初始投资额，Zα表示标准正太分布下置信度α对应的分为数，σ为证券组合的标准差，Δt为持有期。本文选取该法计算VaR。

（二）GARCH模型[2]

ARCH（autoregressive condition heteroskedasticity）是应用于一串金融时间序列，对其波动性进行描述的模型，该模型30年来已广泛的应用到经济学与金融学的计量分析中，是分析金融时间序列的根本模型。在这个模型的基础上，1986年Bollerslev又提出所谓“广义自回归条件异方差”模型（generalized ARCH，GARCH），GARCH（p，q）模型一般公式如下：

其中，p≥0，q>0；α0>0，αi≥0；i=1，…p；βj≥0，j=1，…q。

GARCH模型的出现，对于我们描述收益率的波动性提供了有效的途径。其最简单的形式为GARCH（1，1）模型，基本表达形式为：

（三）GARCH-VaR理论

1.VaR计算。利用GARCH模型计算出的条件方差σ2t，再将随时间变化的条件方差转换成金融资产收益率的方差，结合本论文选取的计算方法，就可以计算出未来一段时期内风险价值VaR预测值。

2.VaR回测检验。回测检验最常用的方法就是失败率检验法。该方法就是对比超过计算出的VaR实际损失的概率与一定置信水平下的上限值是否接近或相等。若通过模型模拟的失败率等于或接近等于预先设定的VaR的置信水平，则说明模型有效；若模拟的失败率与预设置信水平相差太大，则说明模型不恰当。假定置信水平为C，实际考察天数为T，失败天数为N，由二项式过程可以得到在T个样本中发生N次失败的概率为：（1-α）N-TαN[3]。似然比率的计算为：

三、数据处理及检验

本文选取2013年3月25日至2016年4月21日沪深300指数ETF基金每日收盘价数据，剔除节假日等无效数据，共计749个样本点。数据来源于wind，为了减少误差，在这里，我们定义yt为日收益率（%），对数函数的取值范围为全体实数，更适合用于金融建模。因此，本文选取对数收益率来處理：

（一）正态性检检

本文以Matlab为分析工具，利用频数分布直方图来分析沪深300指数ETF基金的日收益率（如图1）。分别对峰度，偏度及Jecque—Bera检验三个指标进行检验。由Matlab处理的结果知，偏度（skewness）为-0.6548，小于0，表明收益率的分布具有左侧长尾特征，实际收益率小于平均收益率的情况较多。峰度（kurtosis）为7.2631，大于3，故其峰度高于正态分布，该分布的尾部要比正态分布尾部要厚，说明存在金融时间序列中“尖峰厚尾”特征。JB检验统计量为1512.344，拒绝原假设，故yt不属于正态分布。

（二）ADF单位根检验[4]

运用GARCH模型的前提条件之一是要求数据平稳。因此，接下来使用ADF检验法对沪深300ETF基金数据的平稳性进行检验。原假设收益率序列存在单位根，运行Matlab可知：ADF检验值为-12.62，小于零界值，拒绝原假设，表明数据不存在单位根。即收益率序列平稳。

（三）相关性检验

利用自相关函数（ACF）和偏自相关函数（PACF）对ETF基金收益率进行检验，并采用Q检验来检验其相关性。原假设是数据不存在序列相关性。利用Eviews8.0软件来处理收益率序列，其输出结果（如图2）。

由图2可知，收益率序列存在高阶的自相关性，因此建立AR（1）模型、MA（1）模型，ARMA（2，2）模型，AR（2）模型，MA（2）模型，A RMA（2，2）模型，AR（3）模型，MA（3）模型，ARMA（3，3）模型，AR（4）模型，MA（4）模型，ARMA（4，4）模型等，经过多次检验，并根据AIC准则和SC准则，发现建立AR（4）模型较好。

3）通过分析可以得到，AR（3）和AR（4）项的系数的t值分别为-0.110507和0.160045；p值分别为0.0023和0，均通过t检验。DW值接近于2，比较显著，无序列相关性；又AIC和CS值比较小，故AR（4）模型更好。

再对其残差序列进行分析，发现残差存在波动的群集现象，由此推断残差存在条件异方差性，需要进行条件异方差检验。

F值与LM值的伴随概率在5%的置信水平下拒绝原假设，即残差序列存在异方差性。

再对残差平方的自相关（AC）与偏自相关（PAC）系数进行分析，结果如下图所示。

由图可知，滞后3阶后的伴随概率明显小于显著性水平0.05。因此，残差序列存在三阶ARCH效应，因此在AR（4）的基础上建立ARCH模型[5]。在条件异方差的情况下往往用GARCH模型替代ARCH模型。

四、实证分析

（一）GARCH（1，1）模型参数估计与检验

在AR（4）模型的基础上建立GARCH（1，1）模型，得到参数估计及检验结果（见下表1）

其中，GARCH（-1）表示GARCH（1，1）模型中的β1项，RESID（-1）^2表示GARCH（1，1）模型中α1项，数据显示GARCH（-1）+RESID（-1）^2<1，满足了GARCH模型的平稳性条件要求β1+α1<1，α0>0以及α1和β1非负，确保了σ2>0。再对该模型滞后一阶进行ARCH效应检验，结果如表2：

F值与LM值的伴随概率在5%的置信水平下接受原假设，即残差序列存在同方差性，纠正了异方差性，消除了ARCH 效应。因此，GARCH（1，1）模型的方程为：

Yt=0.000701-0.073479yt-3+0.091753yt-4

z统计值（1.265436） （-1.986991） （2.247929）

σ2t=0.00000449+0.086214μ2t-1+0.905075σ2t-1

z统计值 （4.576802） （7.896524） （103.1921）

综上分析，GARCH（1，1）可以更有效地控制风险，并且方法简单有效，对沪深300ETF基金的收益率波动有较好的分析能力。

（二）VaR的计算与回测

采用GARCH模型拟合收益率波动方程计算出的VaR值，通过了失败率检验法的回测检验，表明拟合效果较好。

五、结论

与参考文献不同，本文在GARCH模型建立的过程中，不仅检验出沪深300基金收益率存在显著异方差，而且存在高阶自相关，即使使用GARCH模型仍不能完全消除收益率的自相关。因此本文首先对沪深300开放式指数基金建立高阶AR模型利用赤池信息准则和施瓦茨信息准则判断出AR（4）模型的效果最好，然后建立AR（4）-GARCH（1，1），再次检验残差，发现信息已将被完全提取，说明了沪深300指数基金的收益率序列已经被完全刻画，因此利用所建模型计算VaR，并使用LR（似然估计值）进行VaR的预测检验，结果显示AR（4）—GARCH（1，1）模型对于VaR预测效果良好。

一般来说，GARCH模型只能用来消除收益率序列的异方差，即收益率平方的自相关，但是无法消除收益率本身存在的自相关。所以，仅仅采取GARCH模型对收益率建模并不能完全提取数据中所给信息，也就无法准确的预测未来VaR，而收益率之间的自相关只能通过ARMA建模进行处理，因此在进GARCH建模之前一定要确保收益率本身是独立的。只有这样VaR才能被更加準确的预测。

参考文献

[1]刘志永.上证50ETF的风险度量与管理[D].辽宁，辽宁大学，2012年5月.

[2]张成思.金融计量学[M].北京：中国人民大学出版社，2015年4月.

[3]李之好，周海林.两种风险度量方法的研究[J].鸡西大学学报第16卷第4期，2016年4月.

[4]周昭雄，王剑.基于GARCH-VaR模型的ETF基金市场风险的实证分析[J].工业技术经济第29卷第1期，2010年1月.

[5]黄灿.基于GARCH-M模型的中国创业板收益率的实证分析[J].嘉兴学院学报第26卷第6期，2014年11月.

[6]侯敏.我国股指期货的风险度量研究[D].天津，天津财经大学，2011年6月.

作者简介：曾国庆（1994-），男，汉族，安徽芜湖人，安徽财经大学金融学院，研究方向：金融工程。