降雨输入不确定性对SWAT模型径流模拟的影响研究

薛 丰，石 朋,2，胡健伟，瞿思敏，周闫明，李漫漫，谢志刚

(1.河海大学 水文水资源学院，南京 210098；2.河海大学 水文水资源与水利工程科学国家重点实验室，南京 210098；3.水利部水文局，北京 100053)

0 引 言

SWAT(Soil and Water Assessment Tool)模型[1]是美国农业部(USDA)下属的农业研究局(ARS)开发的大中尺度长时段流域分布式水文模型。模型模拟的精度主要受输入变量和参数率定的影响。降雨作为控制水量平衡的重要因素，其在分布式水文模型中的空间描述方案是影响模型模拟精度最为重要的因素之一[2]。张雪松等[3]发现，降雨的空间分布特性和雨量站的密度对SWAT模型的径流模拟有较大影响。Chaplot等[4]基于SWAT模型提出了高密度的雨量站对提高水文模拟精度的重要性。然而我国部分地区目前降雨站点布设并不充足，现有观测资料无法充分反映降雨的空间异质性，影响水文模型的应用效果。雷晓辉等[5]发现在SWAT模型中引入雨量信息空间插值可以提高降雨数据输入精度。宁吉才等[6]通过对比天气发生器和克里金插值对缺测降雨的插补效果，证明了引入降雨空间插值的SWAT模型在径流模拟上的优越性。综上可知，研究降雨空间分布描述方法对发展SWAT分布式模型具有重要意义。

本文将降雨空间插值中较为常用的最邻近法、泰森多边形法、距离平方倒数法和普通克里金法引入SWAT模型子流域面平均雨量的计算，分析模型在多种降雨输入模式下日径流和月径流模拟的精度。考虑到雨量站网密度对雨量插值计算的影响，本文在改变站网密度的条件下进一步比较了不同插值方法对SWAT模型径流模拟的效果，旨在从降雨空间插值方法和站网密度两个方面全面地分析降雨输入不确定性对径流模拟的影响，从而为研究流域建立降雨空间描述方案提供参考。

1 研究方法

1.1 SWAT模型原理

SWAT模型以研究流域的高程信息为基础，实现水系生成和子流域划分。模型假设子流域内的降雨及气象条件具有一致性，数据取自距子流域形心最近的测站。在子流域内部，模型依据土壤分布、土地利用方式和坡度的不同划分水文响应单元HRUs(Hydrological Response Units)。HRUs是SWAT模型最基本的计算单元，模型假设同一个HRU内部具有相同的水文特性，模型运行时在每个HRU上独立地计算产流，最后通过汇流演算推求到流域出口处。

该模型基于严格的物理规律，自开发以来在世界各地得到了广泛的认可和应用。因此，充分开展降雨输入不确定性对SWAT模型的影响研究具有重要的实用价值。

1.2 降雨空间插值算法

降雨空间插值可以将流域内离散的雨量站点数据转化为连续的数据曲面，从而推求范围内其他任意点的雨量值。本文涉及的降雨空间插值算法包括：最邻近法、泰森多边形法、距离平方倒数法和普通克里金法。

1.2.1 最邻近法

最邻近法以待插值站点的位置为圆心由小到大作圆，选取第一个进入绘制的圆形区域内的站点的雨量值作为插值结果的一种插值方法。SWAT模型中的默认插值算法为最邻近插值方法，其计算公式为：

Pj=nearst(Pi)

(1)

式中：Pj为待插值的第j个站点位置；Pi为第i个雨量站的雨量，i=1，2，…，n。

1.2.2 泰森多边形法

泰森多边形法以流域内的测站为顶点形成若干不嵌套三角形，对三角形的三边分别做中垂线，连接中垂线的交点将流域划分成若干个多边形。区域面平均雨量的计算公式为：

(2)

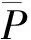
1.2.3 距离平方倒数法

距离平方倒数法是一种加权平均的计算方法，用测站间距离平方的倒数作为权重系数。其计算公式为：

(3)

式中：Pj为第j个测站插得雨量；Pi与第j个测站邻近的第i个测站的雨量；dji为第i与第j测站间的距离；m为第j个测站周围邻近的雨量站个数。

1.2.4 普通克里金法

克里金法实质上是一种局部加权平均的计算方法，其插值公式为：

(4)

式中：z(x0)为x0处的估计值；z(xi)为xi处的观测值；n为观测点个数；λi为克里金权重系数。

克里金法的关键在于确定权重系数λ[7]。本文中应用的克里金法均为普通克里金法，其权重系数的推求过程满足以下两个条件：①估计值误差的数学期望为0，即估计值是无偏的；②估计值误差的方差最小，即估计值是最优的。具体推求过程详见文献[8]。

1.3 评价准则

本文选用纳什系数NSE和相对误差RE作为模型模拟精度的评价指标。

(1)模型效率系数NSE。该指标用于衡量模型模拟径流过程与实测径流过程之间的拟合度。该值越接近于1，则模拟的流量过程越接近观测值，一般NSE≥0.6时，可以认为模拟的结果较好[9]。其计算公式为：

(5)

(2)相对误差RE。该指标用于评价径流总量模拟值和径流总量实测值之间的吻合程度，一般认为相对误差在±20%以内，模拟结果可以接受。其计算公式为：

(6)

式中：qo,i为流量实测值；qs,i为流量模拟值。

2 应用研究

2.1 流域概况

本文选择淮河上游的息县流域作为研究区域。息县水文站控制面积为10 190 km2，流域范围为东经113°15′～114°46′，北纬31°31′～32°43′。息县大体上呈现西高东低的趋势，以平原和缓丘为主，平均海拔为47 m。研究流域位于湿润带与半干旱带的过渡带，多年平均年降雨量为800～1 400 mm，且年内50%的降雨集中在6-9月，多年平均年径流量为300～400 mm。淮河流域地处中国南北气候的过渡带，淮河以北属暖温带，以南为亚热带气候，多年平均气温在14 ℃～16 ℃之间。流域内的土壤类型以水稻土、黄褐土和黄棕壤土为主，土地利用方式主要为耕地和林地。

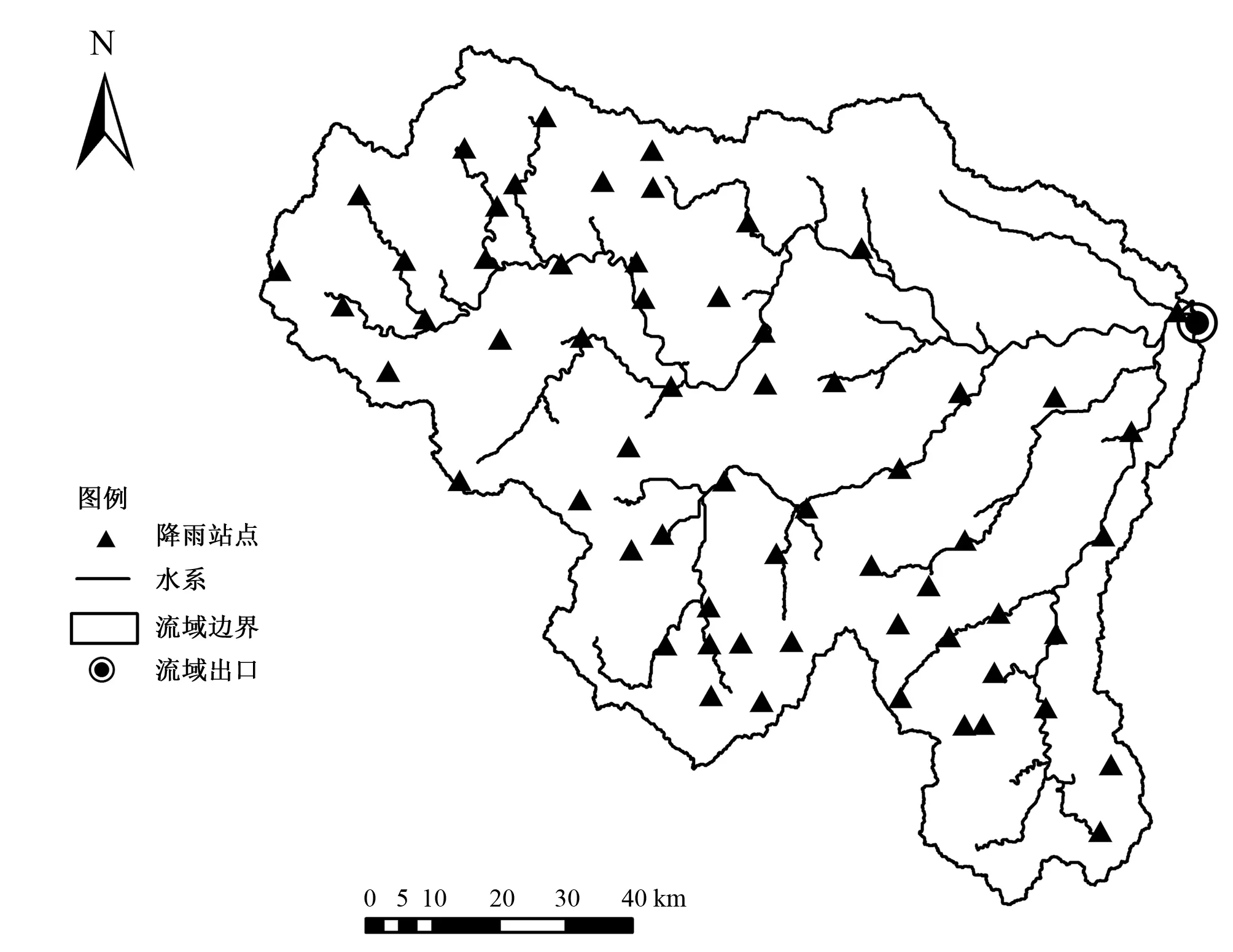
图1 息县流域水系概况图Fig.1 Map of river network in Xixian Watershed

2.2 数据资料

SWAT模型需要用户输入的数据类型分为属性数据和空间数据。属性数据主要包括雨量数据、气象数据和土壤属性数据。本文选用了流域内61个测站1982年到2000年的逐日降水数据，整理了流域内8个气象站的逐日最高最低气温、逐日太阳辐射、逐日平均风速和逐日相对湿度数据。土壤属性数据均参考世界土壤数据库(HWSD)中的数据进行计算。空间数据主要包括数字高程图(DEM)，土地利用图和土壤分布图。本文所使用空间数据的格式、来源及其用途如表1所示，所有空间数据统一采用中央子午线为111°的UTM投影。

表1 原始空间数据说明Tab.1 Description of the original data

2.3 SWAT模型构建

为更好地反映降雨的空间变异性，本文选用较小的集水面积阈值，生成密集水系，最终划分出87个子流域。将息县流域的土壤分布图和土地利用分布图(图2)进行叠加分析，进一步将该区域划分为414个水文响应单元(HRUs)。根据相关文献[10-12]以及现有数据资料，本研究以1982-2000年作为研究期运行SWAT模型。模型应用于实际流域前需将水文资料的60%～70%用于参数率定，其余30%～40%的资料用于检验[13]。因此，本研究选用1985-1995年作为模型率定期，1996-2000年作为验证期，以息县水文站的日(月)径流系列作为实测资料，构建息县流域径流模拟模型。

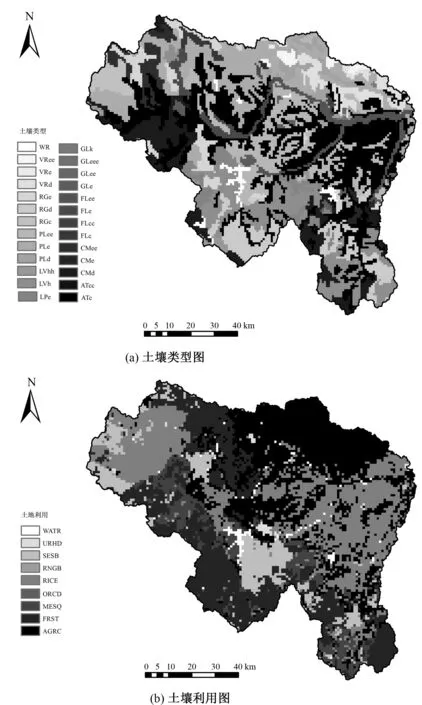
图2 息县流域土壤类型图，土地利用图Fig.2 Maps of distribution of soil type, land use in Xixian Watershed

SWAT模型参数众多，为提高参数率定的工作效率，本文参考SWAT模型参数敏感性分析的相关文献[11,14]，综合考虑下垫面地形、土壤和土地利用等条件，选取7个较为敏感的参数进行率定，分别为：径流曲线数(CN2)、基流退水系数(ALPHA_BF)、地下水滞后系数(GW_DELAY)、浅层地下水径流系数(GWQMN)、土层有效含水量(SOL_AWC)、浅层地下水再蒸发系数(REVAPMN)、主河道冲积物的有效渗透系数(CH_K2)。参数的率定过程基于SWAT—CUP(SWAT-Calibration and Uncertainty Programs)软件，采用SUFI-2算法进行模型参数的自动校准和验证。

3 结果与分析

3.1 不同降雨输入对径流模拟的影响

SWAT模型假设子流域内雨量均匀分布，且数据取自距子流域形心最近的测站。本文在子流域中心设置虚拟的测站，根据就近原则，输入虚拟雨量站的降雨量即为其所在子流域的雨量值。为了充分研究降雨输入不确定性对SWAT模型径流模拟的影响，本文将四种插值方法的计算结果作为虚拟雨量站的降雨输入开展本次研究。虚拟雨量站点分布及泰森多边形分块结果见图3。

图3 流域虚拟雨量站点分布及泰森多边形划分结果图Fig.3 Distribution of virtual raingauges and Thiessen polygons partition

3.1.1 不同降雨插值方法的日径流模拟结果

在SWAT-CUP中利用息县水文站1985-1995年的日径流资料进行参数率定，采用SUFI-2法进行参数不确定性分析，目标函数值趋于稳定时停止迭代。在参数率定的基础上，利用1996-2000年的日径流系列对模型的精度进行验证。日模型的参数率定和验证结果如表2所示。

表2 4种方案日径流模拟评价指标Tab.2 Evaluation of daily runoff simulation results of four schemes

由表2可知，4种降水输入模式的日径流模拟结果NSE均大于0.6，说明SWAT模型在息县流域适应性良好。其中，距离平方倒数法在NSE和RE方面的模拟精度均表现最佳，模型默认的最邻近法在NSE方面表现次之，但在RE方面相较其余方法表现欠佳。在息县流域的日降雨模拟中，在众多文献中认为插值效果较好的克里金方法并未展现出优越性，说明插值方法之间无绝对的优劣性，与其在流域的适用性有较大关联。

3.1.2 不同降雨插值方法的月径流模拟结果

采用相同的方法和相同年份的数据资料，基于息县流域的月径流资料充分率定模型参数，直到达到较为理想的模拟效果。修改模型参数为率定得到的最佳参数，率定期和验证期的模拟结果如表3所示。

由表3可知，4种降雨输入模式的月径流模拟结果均表现优异(NSE>0.85，RE<20%)，但相互之间在NSE方面的差异相较日模拟结果并不显著，这可能是由于实测月径流是流量过程以月为单位的均值，存在一定的均化作用，一定程度上掩盖了各种插值方法之间的差异。在RE方面，距离平方倒数法和泰森多边形法的表现更加稳定，在率定期和验证期均小于5%。

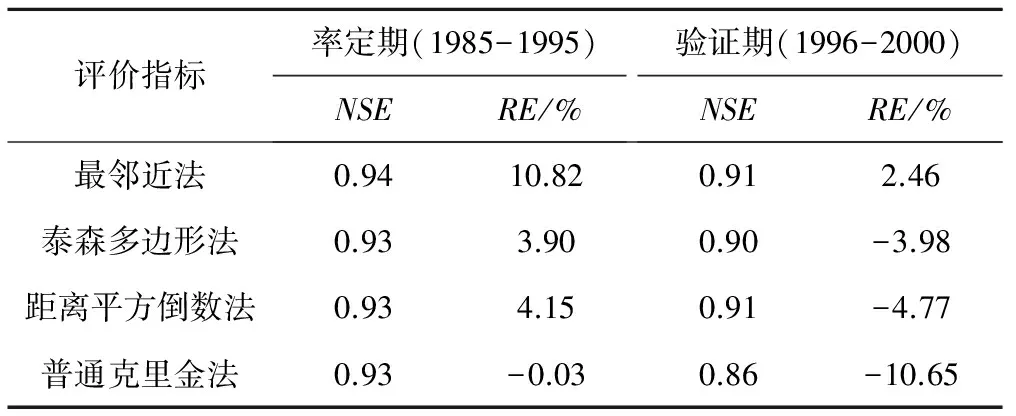
表3 4种方案月径流模拟评价指标Tab.3 Evaluation of monthly runoff simulation results of four schemes

综合考虑4种降雨插值方法在日径流和月径流模拟中的表现，月径流的模拟结果普遍好于日径流模拟，其中距离平方倒数法在息县流域模拟的表现最佳。

3.2 不同站网密度对径流模拟的影响

雨量站网的密度对降雨输入的准确性具有重要影响。本文选用模拟精度较高的月径流系列作为研究对象，在统一模型参数的前提下，分析站网密度对模拟结果的影响。为保证研究结果的全面性，本文分别按空间均匀分布和随机分布的原则筛选25%、50%和75%的雨量站(取整处理后雨量站数目分别为15、30和45)(图4)，重复上述4种插值方法生成雨量序列作为模型输入，开展本次研究。

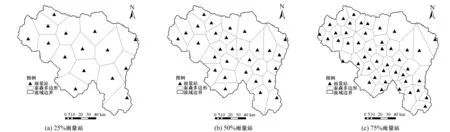
图4 流域降雨站点分布25%雨量站，50%雨量站，75%雨量站和泰森多边形划分Fig.4 Distribution of raingauges 25%, 50%, 75% and Thiessen polygons of Xixian Watershed

按空间均匀分布和随机分布选取雨量站点后的径流模拟结果如图5和图6所示。

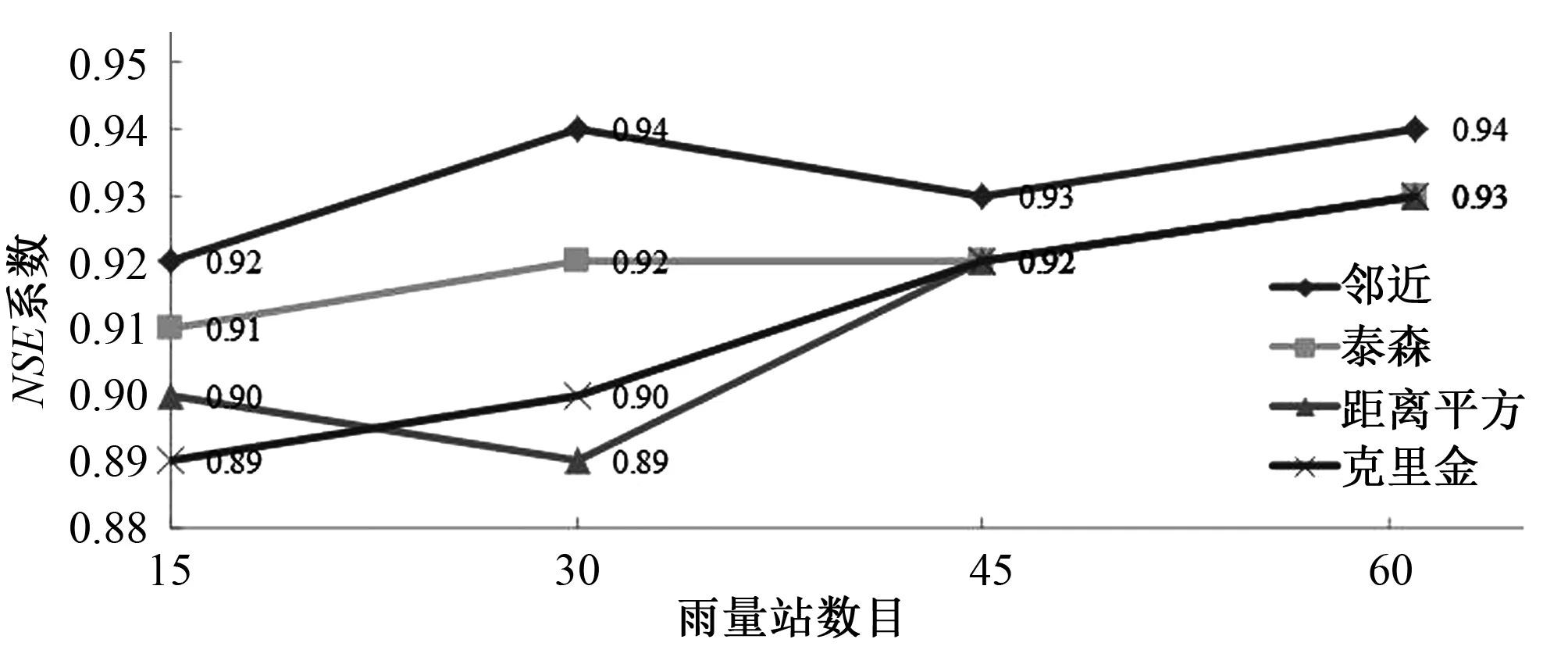
图5 不同降雨输入下的月径流模拟精度(雨量站空间均匀分布)Fig.5 Accuracy of monthly runoff simulation under different xrainfall input(raingauges uniformly distributes)

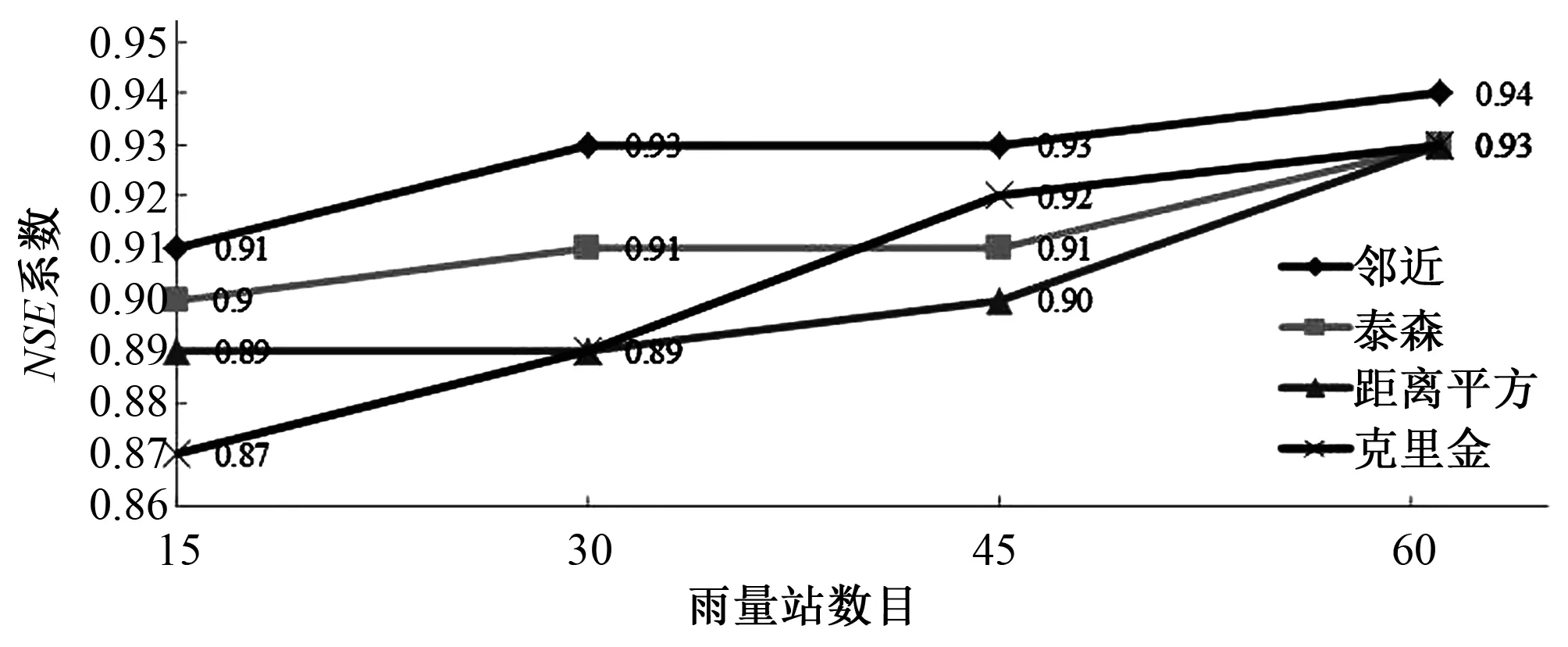
图6 不同降雨输入下的月径流模拟精度(雨量站空间随机分布)Fig.6 Accuracy of monthly runoff simulation under different rainfall input(raingauges randomly distributes)

由图5和图6可知：总体而言，4种降雨插值方法模拟的精度随着雨量站的数目增加而增加，但仍存在一定的不确定性。这一方面是由于降雨空间插值方法存在一定误差。另一方面源于参数的不确定性，本研究所采用的参数方案可能无法反映流域内真实的产汇流规律。另外，随着雨量站数目的增加4种插值方法的模拟精度差异逐渐减小，雨量站密度变化时四种插值方法的精度排序也会发生变化。比较图5和图6的模拟结果可以发现，雨量站在空间位置上的均匀分布一定程度上可以弥补数目减小带来的精度损失。模型默认的插值方法在雨量站数目变化时始终保持最高的模拟精度，泰森多边形法的精度次之，且这两种方法对雨量站数目变化的敏感性较小，当站网密度减小时精度波动不大。

综上可知，模型默认的插值方法的模拟精度相对较为稳定，对雨量站网密度的变化不敏感，在雨量站网密度较少时进行模拟具有一定的优势。

4 结论与展望

本研究基于SWAT分布式水文模型，将最邻近法、泰森多边形法、距离平方倒数法和克里金法四种空间插值方法引入子流域的面雨量计算，分别开展了不同降雨插值方法在日径流和月径流模拟下的精度研究以及不同雨量站网密度对模拟结果的影响研究，得出如下结论：

(1)SWAT模型在息县流域的适用性良好。运用SUFI-2法进行参数率定后，4种降雨输入方案下日径流模拟率定期和验证期的NSE系数均在0.60～0.68之间，相对误差均在±10%以内。月径流的模拟结果普遍优于日径流，率定期和验证期的NSE系数均在0.86～0.94之间，相对误差则在±15%以内。综上，SWAT模型可在该地区进一步推广。

(2)在日径流模拟方面，距离平方倒数法的模拟精度最佳，在月径流模拟时，四种插值方式模拟的精度相差不大，但距离平方倒数法和泰森多边形法的模拟结果更稳定。综合考虑日径流和月径流模拟，距离倒数平方法在息县流域的适应性最好。

(3)总体而言，4种降雨插值方法的模拟精度随着雨量站的数目增加而增加，但仍存在一定的不确定性。在当前雨量站数目的基础上，距离平方倒数法在息县流域的模拟效果最佳。但若在雨量站数目不充足的流域，模型默认的最邻近法在SWAT模型的应用方面可能更具优势。

□

[1] Netisch S L,Arnold J G, Kiniry J R. Soil and water assessment tool’s theoretical documentation[R]. 2009 TWRI report TR:3.

[2] Manguerra H B, B A Engel. Hydrologic parameterization of watersheds for runoff prediction using SWAT[J]. Journal of the American Water Resources Association, 1998,34(5):1 149-1 162.

[3] 张雪松,郝芳华,张建永.降雨空间分布不均匀性对流域径流和泥沙模拟影响研究[J]. 水土保持研究, 2004,11(1):9-12.

[4] Chaplot V, Saleh A, Jaynes D B. Effect of the accuracy of spatial rainfall information on the modeling of water, sediment, and NO3-N loads at the watershed level[J]. Journal of Hydrology, 2005,312(1-4):223-234.

[5] 雷晓辉, 王海潮, 陈 宁,等. 不同气象信息插值算法对SWAT模型模拟的影响研究[C]∥中国水利学会青年科技论坛，2008.

[6] 宁吉才, 刘高焕, 叶 宇,等. SWAT模型降水输入参数的改进研究[J]. 自然资源学报, 2012,27(5):866-875.

[7] 石 朋, 芮孝芳. 降雨空间插值方法的比较与改进[J]. 河海大学学报自然科学版, 2005,33(4):361-365.

[8] Giraldo R, Delicado P, Mateu J. Ordinary Kriging for Function-valued Spatial Data[J]. Environmental & Ecological Statistics, 2011,18(3):411-426.

[9] 薛 晨. 基于SWAT模型的产流产沙模拟与模型参数不确定性分析[D]. 北京：华北电力大学，2011.

[10] 张利茹, 王兴泽, 王国庆,等. 变化环境下水文资料序列的可靠性与一致性分析[J]. 水文, 2015,35(2):39-43.

[11] 杨小强, 石 朋, 包为民,等. SWAT模型在淮河息县流域的参数敏感性及不确定性研究[J]. 中国农村水利水电, 2013,(10):33-36.

[12] 邓 鹏, 李致家. 3种水文模型在淮河息县流域洪水模拟中的比较[J]. 河海大学学报(自然科学版), 2013,(5):377-382.

[13] 李致家, 孔凡哲, 王 栋, 等. 现代水文模拟与预报技术[M]. 南京：河海大学出版社, 2010.

[14] 黄清华, 张万昌. SWAT模型参数敏感性分析及应用[J]. 干旱区地理, 2010,33(1):8-15.