基于小波变换的径流与降水时频变化及相关性分析----以五郎河为例

陈一明，何子杰，贲 月，董庆华

(1.长江勘测规划设计研究院，武汉 430010；2.武汉大学水资源与水电工程科学国家重点实验室，武汉 430072)

五郎河属金沙江一级支流，是金沙江上游一条重要支流，具有丰富的水能资源，地跨丽江市宁蒗、永胜两县。随着丽江市旅游业迅速发展，永胜县供大于求的用水矛盾以及程海水生态环境恶化的问题日益凸显。因此，探讨五郎河流域径流的变化规律及影响因素，不仅可为该流域水资源的开发利用提供重要的参考依据，而且对当地生态环境保护、生态环境建设具有重要指导意义。

径流和降水是水文循环的基本要素，其变化均具有复杂的随机性和不确定性，而降水又是影响径流的水文气象因素之一，因此对径流变化的规律和特点的描述及其影响因素的相关性探寻一直是水文领域研究的重点。小波变换是在窗口傅里叶变换的基础上发展起来的，是一种分析信号的新方法[1]，其良好的时-频局部性及多分辨率特点使其广泛应用于水文领域，尤其是对非平稳的水文时间序列的分析[2,3]。而径流与降水均是非平稳却又能呈现一定的周期变化的时间序列，因此运用小波变换对它们的时-频变化进行多尺度分析，可以得到径流与降水时间序列主要尺度以及各尺度下的“丰-枯”和“多-少”变化过程，从而可预测它们在各尺度下的变化趋势。

交叉小波分析是一种将小波功率谱与交叉谱结合起来的一种新方法[4-6]，该方法可以对两个非平稳时间序列间的相关程度进行有效分析，能够揭示两者在特定时间尺度和频域上的相位关系，从而能更深层地理解两个时间序列间互相关关系。

本文基于五郎河流域主要测站实测径流资料及丽江气象站降水资料，采用Morlet小波变换法，分别对五郎河56年(1959-2014年)以来年径流量以及丽江同时间段(1959-2014年)的年降水的变化特性及其变化规律进行分析，并运用交叉小波分析方法，对径流和降水在时域和频域中的多尺度相关性及其周期性进行分析，与传统的方法相比，能够更精确地评估五郎河径流变化趋势以及降水对径流的影响，为更好地开发利用五郎河流域水资源提供了理论基础。

1 研究区域

五郎河系金沙江的一级支流，地跨丽江市宁蒗、永胜两县，河长约为98.1 km，落差2 270 m，经战河乡、西布河乡后，横穿永胜县北部，在永胜县太安乡汇入金沙江干流。五郎河流域面积2 088 km2，分水岭高程一般在3 000 m以上，上游穿行于峡谷之中，水流湍急；支流呈扇形分布；下游两岸地形开阔，为三川盆地(图1)。

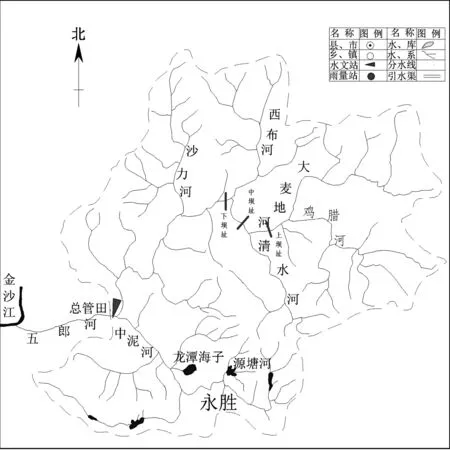
图1 五郎河流域水系图Fig.1 Wulang River Basin

五郎河流域属横断山系的高山峡谷区，河流两岸陡峭险峻，呈“V”字形。该流域属于暖温带季风气候，干湿季分明，夏秋多雨，冬春多旱，霜期较长，湿度大，多年平均相对湿度为69%，流域东西差异较大，气候垂直变化显著，河谷地带地势较低，气温较高，降水较少，属中亚热带或南亚热带气候。流域内多年平均气温为13.7 ℃，多年平均降水量为951 mm。

2 研究方法和数据来源

2.1 小波变换

小波变换是通过将时间序列分解到时域和频率域内，从而得出时间序列的显著的波动模式，即周期变化，以及周期变化的时间格局。小波变换分为连续小波变换(Continuous Wavelet Transform, CWT)和离散小波变换(Discrete Wavelet Transform, DWT)，DWT是数据的紧凑表示，常用于降噪与数据压缩处理；而CWT适用于信号特征的提取[4]。由CWT变化的结果得到的小波系数表示时间序列与小波的近似程度。目前，Morlet小波函数因其与径流、降水、气温等时间序列的波形相似，且可以探测时间序列在不同频域中时域的振幅和相位，极好的表现出时-频域的局部特征的优势[7,8]，被广泛应用于水文气象时间序列中[9,10]。因此，本文采用Morlet复值小波对径流和降水时间序列进行小波变换。小波变换及Morlet小波变换理论具体方法详情参见文献[4,7,8,11]。

2.2 交叉小波变换

将小波变换与交叉谱分析相结合的方法称之为交叉小波变换，它是一种可以从多尺度来分析两个时间序列在不同时域和频域中的相互作用显著性的新方法[12]。在两个时间序列的连续小波谱的基础上，构造两者的交叉小波谱(Cross Wavelet Transform, WTC)，可以反映两个时间序列的在不同时频域上所具有相同或相近能量谱区域的范围，该能量谱值越大，表示两时间序列在不同时频域上相互作用的越显著。

为了更好地研究两个水文序列之间的相关关系，引入小波相干谱(Wavelet Coherence,WC)或凝聚谱，旨在揭示两个时间序列间互相关性对频域的依赖程度。具体交叉小波谱及小波相干谱理论方法参见文献[5,7,12-14]。

2.3 数据来源

由于总管田水文站为五郎河流域的控制站，因此本研究以总管田水文站为主，收集了总管田水文站的实测径流资料(1959-2014年)。丽江气象站降水资料(1959-2014年)来源中国气象数据网(http://data.cma.cn/)。为了避免径流和降水时间序列中极端天气变化误差的干扰，运用SPSS统计分析软件，分别对年径流量和年降水量统计数据进行标准化处理。

3 结果分析

3.1 周期变化特性分析

通过Morlet复值小波方法分别对总管田水文站和丽江气象站56 a(1959-2014年)标准化年径流序列和降水序列进行连续小波变换，分析小波变换系数的实部、模平方、方差等信息，揭示年径流变化和年降水的多时间尺度变化规律。

3.1.1 小波系数实部时频分析

小波系数实部可以反映时间序列在不同时间尺度下的周期变化及其在时间域中的分布情况，进而可以判断在不同时间尺度上，时间序列的未来变化趋势[15-19]。

图2(a)和2(c)为标准化年径流和年降水序列小波系数实部等值线图。小波系数实部大于0时，表示径流量偏丰[图2(a)和2(c)中深色区域]；相应地，若小波系数实部小于0时，表示径流量偏枯[图2(a)和2(c)中浅色区域]；而小波系数等于0时，则表示径流处于平水期。图2(a)和2(c)均呈现出明显的年际变化(10年以下)和年代际(10年以上)变化，即从大尺度至小尺度(纵坐标由上至下)来看：

(1)对于径流[图2(a)]，存在2种尺度的周期变化：6～28 a和2～5 a，这两种尺度下丰、枯交替变化较明显，贯穿整个时间序列，而30 a以上的尺度并未看到明显的周期变化。从大尺度6～28 a来看，径流随着时间序列变化(横坐标由左至右)表现出了“枯-丰”交替的准两次震荡，存在明显的突变特性，具体表现为1959-1964年偏枯，1968-1976年偏丰，1984-1998年偏枯、2002-2014年偏丰，整个尺度的周期变化在整个时间序列中的状态很稳定，占据了整个时间序列，具有全域性；而小尺度2～5 a的周期变化，主要在1960s-2000s表现得较为活跃，存在“枯-丰-枯”的周期变化。

(2)对于降水[图2(c)]，存在3种尺度的周期变化：16～28 a、9～14 a和4～8 a，其中16～28 a、4～8 a尺度的多-少交替变化表现较明显，贯穿整个时间序列，而30 a以上的尺度除了局部包含在16～28 a的闭合范围内之外，其余也并未看出明显的周期变化。从大尺度16～28 a分析，降水量出现“少-多”交替的准5次震荡，突变特性明显，且从图2(c)中可以观察到，在整个时间序列中振荡最强的时间尺度均出现在这一范围内，表现很稳定，说明该尺度在整个时间序列中具有全域性；9～14 a的周期变化主要在1960s-1990s表现较活跃，降水量出现“多-少”交替的准4次振荡；而小尺度4～8 a的周期变化，存在“少-多-少”周期变换。

比较图2(a)和2(c)可知，尽管径流和降水的周期变化并不十分一致，但两者存在全部包含和部分包含的关系，如径流的大尺度6～28 a是包含了降水的16～28 a和9～14 a，但径流的小尺度2～5 a与降水的4～8 a只是部分包含的关系。此外，从图2(a)和图2(c)中还可以发现，无论是径流还是降水，均存在若干小尺度下的丰-枯期(多雨-少雨期)嵌套在一个大尺度下的偏丰期(多雨期)或者偏枯期(少雨期)的现象，小尺度下的突变点要比大尺度多，且各时间尺度下的突变点个数及其所在的时间位点均不同，因此应在具体时间尺度研究突变点。

3.1.2 小波能量多尺度特征

小波系数的模平方即为小波能量谱，可以分析时间序列在不同周期下的振荡能量。图2(b)和2(d)分别为标准化年径流和年降水序列小波系数等值线模平方图。

(1)年径流：从图2(b)可以观察到，在整个径流时间序列中8～18 a时间尺度能量最强，表现出的周期性最明显，其中心点对应11～12 a。但它的周期变化具有局限性(1999年后)；2～5 a尺度的周期振荡强度次之，其他时间尺度的周期变化不明显。这一分析结果与上文分析的6～28 a和2～5 a周期变化基本一致。

(2)年降水：从图2(d)中可以看出，在整个降水时间序列中表现出的能量最强、周期性最明显的时间尺度为16～24 a，且其中心点不唯一，分布在1960-1974年间和1990-1995年间，同样，它的周期变化也具有局限性(2009年前)；8～12 a和4～7 a尺度的周期振荡强度次之，其他时间尺度的周期性变化不明显。显然，这一结果与上文所分析的16～28 a、9～14 a和4～8 a周期变化基本一致。

比较图2(b)和2(d)可知，尽管年径流与年降水周期最明显的时间尺度不一致，但从整体来看，两者的周期变化基本一致；两者的周期变换均具有局限性，年径流表现更明显。

3.1.3 小波方差检验主周期

小波方差图是刻画的是小波方差随时间尺度的变化过程，可以找出水文时间序列在其形成过程中所存在的主周期[11]。图3(a)和3(c)分别为年径流和年降水小波方差图。

可以看出，图3(a)中存在2个峰值，从左至右分别对应3 a和12 a时间尺度，其中，12 a左右的周期振幅最大，为此径流序列变化的第一主周期，则3 a为次主周期；而图3(c)中明显看到有4个峰值，从左至右分别对应4、6、18和26 a时间尺度，其中，18 a左右的周期振荡最强，为此降水序列变化的第一主周期，则4 a和6 a分别为第二、第三主周期。两者的分析结果均分别在小波能量谱的分析结果范围内。

3.1.4 不同周期尺度的丰-枯(多-少)变化分析

基于小波方差检验的结果，选择振荡较强的主周期绘制相应尺度下的小波系数实部图，分析不同时间尺度下，水文时间序列的平均周期及其丰-枯(多-少)变化规律。图3(b)和图3(d)分别为年径流和年降水在主周期尺度下的小波变换实部图。图中，小波变换实部>0时代表流量较大，实部<0时表示流量较小，不同尺度对应不同的丰-枯(多-少)变化。

(1)年径流：从图3(b)可知，在12 a时间尺度下，径流序列经历约1.5个波动周期，径流丰枯的突变点在1964-1965(枯-丰)、1980-1981(丰-枯)，1997-1998(枯-丰)，2007年处于该尺度下的偏丰阶段的波动极大值处。从变化趋势可以预测2014年后径流的变化趋势为逐渐减少，同时，还可以预测在12 a时间尺度(2022年前后)径流将由枯变丰；在3 a时间尺度下，径流丰枯的突变点在1965-1966(枯-丰)、1970-1971(丰-枯)、1973-1974(枯-丰)，1977-1978(丰-枯)，1979-1980(枯-丰)，1982-1983(丰-枯)，1986-1987(枯-丰)，1987-1988(丰-枯)，1990-1991(枯-丰)，1994-1995(丰-枯)，2000-2001(枯-丰)，2012-2013(丰-枯)，同样，从变化趋势可以预测2014年以后径流有减少的趋势，且在3 a时间尺度(2018年左右)径流将由枯转丰。

(2)年降水：从图4(d)可知，在18年时间尺度下，降水序列经历约3个波动周期，其变化的平均周期约为18 a；降水量丰枯的突变点在1962-1963(少-多)、1968-1969(多-少)，1974-1975(少-多)，1980-1981(多-少)，1986-1987(少-多)，1992-1993(多-少)，1998-1999(少-多)，2003-2004(多-少)，2009-2010(少-多)。从变化趋势可以预测2014年后径流的变化趋势将逐渐减少，同时，还可以预测在18 a时间尺度(2024年左右)降水量将由少变多。在6 a和4 a时间尺度下，降水序列分别经历9个和9.5个周期波动，其变化的平均周期分别约为6 a和5.9 a。从变化趋势来看，6 a时间尺度下，预测2014年以后降水量有增加的趋势，且在2017年左右降水量由多雨期转为少雨期，而4 a时间尺度下，预测2014年以后降水量有减少的趋势，且在2016年降水量由少雨期转多雨期。

比较分析图4(b)和图4(d)可知，年径流在各尺度下的平均周期均比年降水要大，而从两者的第一主周期来说，其预测2014年后径流和降水均有减少的趋势，但仍然处于丰水(多雨)期，分别在8 a和10 a后由丰(多)转枯(少)。此外，由两图可以看出，小尺度的丰-枯(多-少)交替变化是嵌套在大尺度的丰-枯(多-少)结构中，即大尺度为丰(多)时，对应的小尺度可能是枯(少)，反之，亦然。这与3.1.1节的分析结果一致。

图3 年径流和年降水时间序列小波方差图及不同尺度下小波实部图Fig.3 Wavelet variance diagram and wavelet real parts under different scales of runoff and precipitation time series data

3.2 径流与降水量相关关系分析

基于上述小波变换，对五郎河年径流量与丽江站年降水量的小波系数进行相关性分析，通过对连续小波变换后的系数进行交叉小波变换和小波相干变换，分析两时间序列相互间的交叉小波能量谱和小波相干谱，进而探讨两者在不同时间尺度下时频域的相关程度。图4展示了五郎河流域径流和丽江站降水量的交叉小波功率谱和小波相干谱。图中箭头表示两者之间的位相关系，箭头向右和向左分别表示径流与降水之间为同位相和反位相，说明两者呈正(负)相关关系，箭头向下和向上分别表示降水变化超前和落后径流变化90°。图中细弧线以内区域为有效谱值[20]。从图4(a)中可以看出，总管田站径流与丽江站降水存在：①1～4 a(1964-1970年)的周期，呈现较好的正相关，高能量区主要集中在低中频部分的1～3 a，且从低频向高频区逐渐过渡；②1～3 a(1994-1999年)、2～3 a(2003-2006年)、5～7 a(1977-1981年)的共振周期，置信度检验的区域相对较小，表现出间歇性的准周期振荡。

两序列的小波凝聚谱显示[图4(b)]，径流与降水具有非常好的正相关性，通过显著性检验的区域占整个有效谱值区域范围内的90%左右，在4～6 a的周期上，1970年和1990年前后，其共振周期发生了突变，说明五郎河流域在该时段发生了“丰-枯”周期的转变。两序列的共振周期高能量区主要分布在1968年前后和1985年前后2 a、1970-1995年6 a左右的周期，以及1975-2000年的12 a左右的周期。

结合交叉小波能量谱和交叉小波凝聚谱，发现：①五郎河流域径流与丽江站降水变化存在2～4 a的显著性共振周期，说明降水对径流的影响很大。②两者表现为非常显著的正相关性，说明丽江站降水量可作为五郎河流域径流预测的控制因素。③径流和降水在1970和1990年前后发生了“丰-枯”的突变。

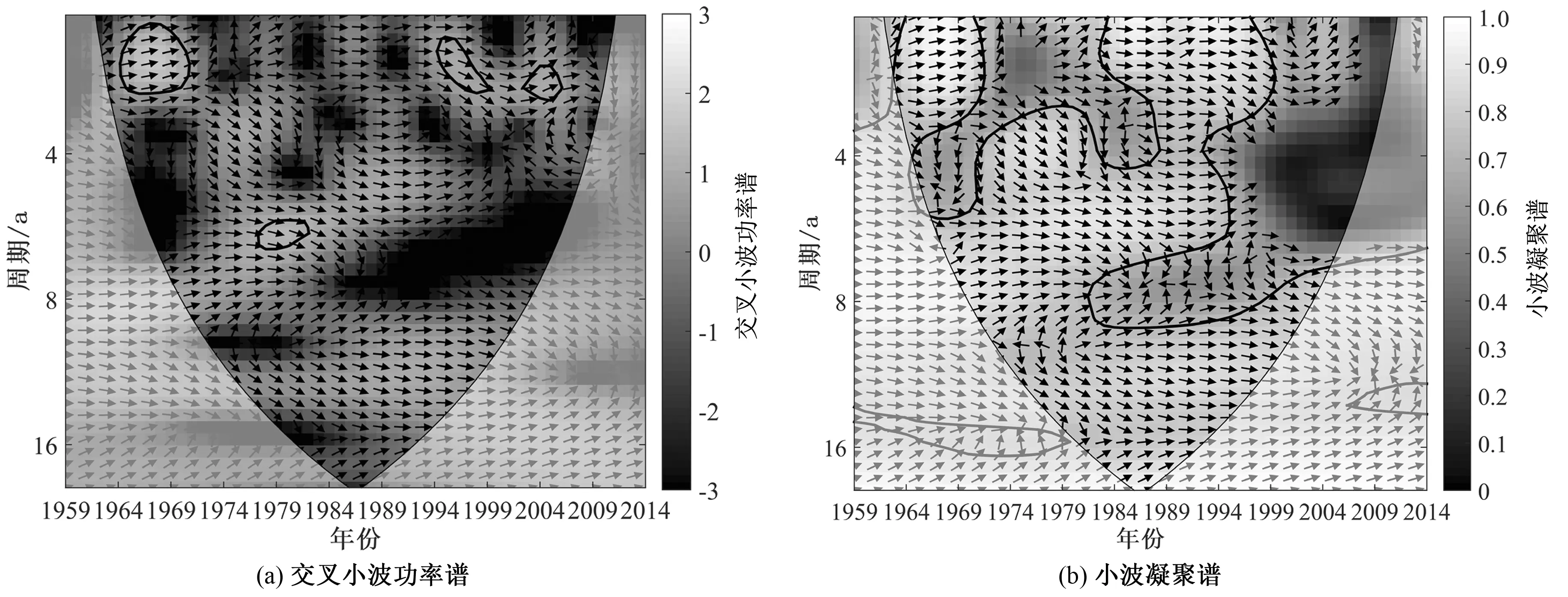
图4 径流与降水的交叉小波功率谱与小波凝聚谱Fig.4 Cross-wavelet power spectrum and squared wavelet coherence between the runoff and precipitation time series

4 结 论

本文通过对五郎河总管田水文站和丽江气象站56年间的数据进行小波分析，得到五郎河径流量和丽江站降水的周期特性，并运用交叉小波变换，分析了它们在时频域中的相关关系，具体结论如下：

(1)通过小波变换的系数实部、模平方等值线图及小波方差图，可知，五郎河流域总管田水文站的径流量在1959-2014年间丰枯变化明显，存在6～28 a和2～5 a 2种尺度的周期变化，其中12 a是第一周期，3 a强度略弱，是第二周期。同时预测2014年后径流均有减少的趋势，且在12 a时间尺度下，2022年前后径流将由枯变丰；

(2)通过对降水序列的统计特性分析和小波分析，可知，丽江站降水存在16～28 a、9～14 a和4～8 a 3种尺度的周期变化规律，其中18 a为第一周期，4 a、6 a分别为第二和第三周期；同时预测在18 a时间尺度，2024年左右降水量将由少变多；

(3)交叉小波凝聚谱和小波相干功率谱显示，总管田站年均径流与丽江站年降水存在2～4 a的显著性的共振周期，且两者呈现出非常好的一致性，说明丽江站降水量可作为五郎河流域径流预测的控制因素。

(4)五郎河径流量变化是各种水文气象因子多重交互作用的结果，其中降水变化是径流变化的主导因素之一，但径流的变化与其他多重气象因子之间的交互影响有待进一步研究。此外，在本文中采用的时间尺度为年，而无法体现年内的细节变化，还需更深入的分析和研究。

□

[1] 王文圣, 丁 晶, 李跃清, 等. 水文小波分析[M]. 北京: 化学工业出版社, 2005.

[2] 桑燕芳, 王中根, 刘昌明. 小波分析方法在水文学研究中的应用现状及展望[J]. 地理科学进展, 2013,32(9):1 413-1 422.

[3] 张少文, 丁 晶, 廖 杰, 等. 基于小波的黄河上游天然年径流变化特性分析[J]. 四川大学学报: 工程科学版, 2004,36(3):32-37.

[4] Grinsted A, Moore J C, Jevrejeva S. Application of the cross wavelet transform and wavelet coherence to geophysical time series[J]. Nonlinear Processes in Geophysics, 2004,11(5/6):561-566.

[5] 孙卫国, 程炳岩. 交叉小波变换在区域气候分析中的应用[J]. 应用气象学报, 2008,19(4):479-487.

[6] 余丹丹, 张 韧, 洪 梅, 等． 基于交叉小波与小波相干的西太平洋副高与东亚夏季风系统的关联性分析[J]. 南京气象学院学报, 2007,30(6):755-769.

[7] Torrence C, Compo G P. A practical guide to wavelet analysis[J]. Bulletin of the American Meteorological Society, 1998,79(1): 61-78.

[8] Lau K M, Weng H Y. Climate signal detection using wavelet transform: How to make a time series sing[J]. Bulletin of the American Meteorolgical Society, 1995,76(12):2391-2 402.

[9] 安 全, 梁 川, 刘 政. 雅砻江中上游径流变化特性的小波分析[J]. 武汉大学学报(工学版), 2008,41(3):20-28.

[10] 马海波，郭慧芳，董增川, 等. 鄱阳湖出湖径流序列的多时间尺度小波分析[J]. 人民长江,2011,42(11): 53-55.

[11] 薛小杰, 蒋晓辉, 黄 强, 等. 小波分析在水文序列趋势分析中的应用[J]. 应用科学, 2002,20(4):426-428.

[12] Torrence C, Webster P J. Interdecadal Changes in the ENSO-Monsoon system[J]. Journal of Climate, 1999,12:2 679-2690.

[13] 丁裕国, 江志红.气象数据时间序列信号处理[M].北京:气象出版社, 1998:278-283.

[14] Maraun D，Kurths J. Cross wavelet analysis: significance testing and pitfalls[J]. Nonlinear Processes in Geophysics, 2004,11(4):505-514.

[15] Nakken M. Wavelet analysis of rainfall runoff variability isolating climatic from anthropogenic patterns[J]. Environmental Modelling & Software, 1999,14(4):283-295.

[16] Nason G P, Sapatinas T. Wavelet packet transfer function modelling of nonstationary time series[J]. Statistics and Computing, 2002,12(1):45-56.

[17] 邓凯旭, 宋宝瑞. 小波变换在金融数据分析中的应用[J]. 数理统计与管理, 2006,25(2):215-219.

[18] Chen J X, Wang W J. Wavelet-based interpolation of medical images[J]. Journal of System Simulation, 2007,19(1):145-149.

[19] 刘笑彤, 蔡运龙. 基于小波分析的径流特性和影响因素多尺度分析----以通天河为例[J]. 北京大学学报(自然科学版), 2014,50(3):549-556.

[20] 邵 骏. 基于交叉小波变换的水文多尺度相关分析[J]. 水力发电学报, 2013,32(2):22-26.