基于Abaqus的轻型汽车牵引装置强度分析

徐余平++刘俊红++张雷

摘要： 为保证汽车牵引装置强度满足最新的国标要求，运用Abaqus中的非线性有限元方法对某轻型汽车的后部牵引装置进行强度分析.通过试验与仿真结果的对比找出牵引装置的薄弱区域和失效原因，并提出避免地板屈曲失稳的优化方案.仿真和试验结果表明优化方案满足设计要求.

关键词： 轻型汽车； 牵引装置； 强度； 屈曲失稳； 屈服； 优化； 有限元

中图分类号： U467.3文献标志码： B

Lightweight car traction device strength

analysis based on Abaqus

XU Yuping， LIU Junhong， ZHANG Lei

（Technology Center， Anhui Jianghuai Automobile Group Co.， Ltd.， Hefei 230001， China）

Abstract： To ensure the strength of the automotive traction device to meet the requirements of the latest national standard of China， the nonlinear finite element method in Abaqus is used to analyze the strength of the rear traction device of a lightweight car. By comparison of the results of test and analysis， the weak area and the failure reason are found and an optimization scheme is proposed for avoiding buckling of floor. The results of simulation and test show that the optimization scheme meet the design requirements.

Key words： lightweight car； traction device； strength； buckling； yield； optimization； finite element

收稿日期： 2016[KG*9〗11[KG*9〗08修回日期： 2016[KG*9〗12[KG*9〗19

作者简介： 徐余平（1988—），男，安徽合肥人，工程师，研究方向为车身疲劳和强度性能开发，（Email）autolotus@126.com0引言

牵引装置一般包括牵引钩（拖钩）、安装板及相关附件.作为一种安全保护装置，牵引装置通常装配在汽车前后保险杠或者地板上，以便车体进入危险环境后，能借助拖绳、拖杆等外力脱离困境.牵引装置应该具备足够的强度，以保证其使用要求.[1]

国家标准化管理委员会在2015年10月9日发布国家强制性标准（简称国标）《轻型汽车牵引装置》（GB 32087—2015），2016年7月1日正式实施.[2]该标准要求新开发车型必须执行此标准，已上市车型在标准实施后有1 a的整改期.

该标准是轻型汽车牵引装置的强制要求，如果试验不满足要求就无法上市销售.以往对牵引装置的强度分析仅考虑材料的非线性，进行简单的带角度拉伸，未考虑压缩情况[1，34]，容易导致分析结果与试验结果不一致.本文采用Abaqus的非線性有限元方法，介绍基于国标工况下的牵引装置强度分析，充分考虑非线性问题的影响，并且在分析中引入屈曲失稳理论，对压缩工况下地板的大变形进行研究，给出避免失稳的改进方案，为牵引装置的强度性能开发提供参考和指导.1Abaqus软件的非线性理论

Abaqus是功能强大的有限元软件，可以分析复杂的非线性问题，在汽车行业中应用广泛.在真实的物理结构中，结构的刚度会随着变形而发生改变，即为非线性.Abaqus软件在非线性模拟领域具有很强的优势.非线性问题可以分为3类：材料非线性、边界非线性和几何非线性.[57]

材料非线性，即金属材料弹性模量在小应变时为常数，当应力超过屈服点后，刚度会急剧下降，产生不可恢复的塑性应变.

边界非线性，即边界条件随分析过程发生变化.接触问题是一种典型的边界非线性问题，其特点是边界条件不是计算开始就可以全部给出，而是在计算过程中确定的.例如图1，梁端部在变形过程中碰到障碍后系统的刚度才发生急剧变化.

图 1边界非线性

Fig.1Boundary nonlinearity

几何非线性，即位移的大小对结构响应产生影响，包括大位移、大转动，突然塌陷或翻转等.由于无法判断分析过程中是否会出现较大的变形，因此一般在分析过程中默认要考虑几何非线性的影响.塌陷是一种高度非线性的现象，又称为屈曲失稳，最典型的例子就是细长杆偏心受压现象，见图2中的AB段.

图2中，当载荷P达到载荷PU以后，即使载荷P不增加甚至减小，也不能阻止结构变形的急剧增大（即BC段）.载荷PU就是杆件的失稳载荷.[810]

为求解非线性平衡问题，在Abaqus/Standard中使用基于NewtonRaphson增量迭代法，具体过程[5]可以描述如下.

（1）静态平衡的基本表达式为由单元应力引起的加在节点上的内力I与外力P必须平衡，即P（u）-I（u）=0 （1）（2）假定前一步载荷增量的解u0和P0为已知.

（3）在当前增量步中，将一个小的载荷增量ΔP施加到结构上.

（4）Abaqus基于u0处的切线刚度K0确定位移修正c1，前一增量步结束时，总载荷PTOTAL与内力间的关系为K0c1=PTOTAL-I0 （2）（5）Abaqus更新模型的状态为u1，形成K1并计算I1.

（6）第二次迭代基于更新的刚度K1，计算新的位移修正c2，并且K1c2=PTOTAL-I1 （3）（7）一直重复该过程，直到力的残差（总载荷PTOTAL与内力I1的差）在允许的容差之内，见图3.

图 3NewtonRaphson迭代

Fig.3NewtonRaphson iteration

NewtonRaphson迭代法在求解结构的屈曲稳定问题时，一旦所施加的载荷达到临界值，就会出现系统刚度矩阵的奇异，从而给系统方程组的求解带来困难，甚至导致求解的失败.此时，软件会自动降低载荷增量，逐步逼近结构的极限载荷，载荷位移曲线出现水平段，但是这种逼近仍然无法越过极值点，更不能跟踪载荷下降段的系统响应.Abaqus/Standard提供的弧长法在一定程度上可以解决这一问题，通过追踪整个失稳过程中实际的载荷位移关系获得结构失稳前后的全部响应.[89]

对于绝大多数情况，结构一旦发生屈曲失稳，就失去使用功能，因此我们在产品设计过程中只需要避免结构发生屈曲失稳，不用过度关心结构在失稳后的载荷位移响应.

2国标介绍

国标《轻型汽车牵引装置》（GB 32087—2015）在2016年7月开始正式实施.标准适用于最大允许总质量不大于3.5 t的M类车以及N1类车.标准规定：“汽车应在其前部至少固定或可安装一个牵引装置，即拖钩.若汽车在后部安装了牵引装置，则牵引装置应符合本标准的技术要求.”

牵引装置应该能承受的最小静载荷F=m×g/2 （4） 式中：F为牵引装置承受的最小静载荷，单位N；m为最大允许总质量，单位为kg；g为重力加速度，取9.8 m/s2.

安装在车辆上的每一个牵引装置应按照图4的角度进行加载测试.

国标规定的加载方向总共有10个：水平方向的拉伸和压缩、左右25°的拉伸和压缩、上下5°的拉伸和压缩.其中水平方向上的拉压是国标规定必须测试的，其余8个方向随机抽取2个测试.

国标要求牵引装置及其固定件不应失效、断裂或产生影响正常使用的变形，且安装在牵引装置附近的其他部件不应出现影响整车工作的损坏.

3牵引装置强度性能分析

3.1国标试验情况

某车型在开发阶段仅对车辆前部牵引装置进行拉伸强度分析，未考虑后部的牵引装置强度.本轮国标的实施，要求前后牵引装置都应满足国标技术要求，在进行国标试验的水平压缩工况时，当压力加载到4 000 N时，后地板产生很大变形，试验失败.试验弯折照片见图5，可以看出，地板加强梁在与拖钩安装板的搭接处（标志区域）折弯，将地板顶起，变形很大.

经过对试验车辆的拆解，可以看出试验车辆此处焊点满足设计要求，钣金厚度与设计一致，牵引装置的设计状态图见图6.排除工艺原因，判定是牵引装置的强度不足导致试验失败，需要对牵引装置进行强度分析.采用国标加载工况，复现试验结果，并提出优化方案.由于试验过程中出现明显的非线性现象，故采用Abaqus软件进行非线性强度分析.a）加强梁

b）地板

1—拖钩；2—安装板；3—地板加强梁；4—地板

3.2牵引装置强度分析模型建立

3.2.1网格建立

模型的处理使用HyperMesh，拖钩采用3 mm六面体单元C3D8I进行划分，安装板采用3 mm壳单元S4进行划分，地板和其他钣金采用8 mm的整车网格标准划分.拖钩与安装板是二保焊连接，采用KINCOUP單元模拟.另外，为避免不合理的应力集中现象，需要保证KINCOUP单元一一对应且垂直.车身的焊点采用ACM单元模拟.[4]

3.2.2材料和属性

牵引装置的材料及其厚度见表1.考虑材料的非线性因素，整个牵引装置都需要定义材料的塑性阶段.

3.2.3接触非线性

由于分析中可能出现大变形，导致钣金与钣金触碰，属于典型的非线性现象，因此需要在地板、安装板、拖钩等可能触碰的区域建立接触关系.Abaqus提供2种建立接触的方式：接触对和通用接触.接触对需要手动定义接触区域，包括主面和从面；通用接触会自动建立接触面，两者各有优劣.本分析采用Abaqus里的通用接触算法.

表 1材料属性

Tab.1Material property零件名板厚/mm 材料拖钩实体20#钢安装板 1.2B340LA地板加强梁 0.7DC03地板 0.7DC04

3.2.4工况和目标

该车型的最大总质量为1 387 kg，根据国标要求的载荷计算方法，加载力为F=1387 kg×9.8/2 m/s2=6796.3 N （5）约束车身截取处，在拖钩上施加载荷并卸载.方向与国标要求一致，总共考察10个工况.

目标值分2个方面：对等效塑性应变PEEQ进行定量评价且比国标严格，即要求PEEQ的值小于15%，避免断裂；对变形进行定性的风险等级评估，认为最大变形>30 mm，残余变形>15 mm即存在较大风险.

3.3分析结论

由于国标试验在进行水平压缩工况时出现失效，为方便比较，现提取水平压缩工况的位移和应变结果，见图7.

由图7可以看出：地板加强梁后部与拖钩安装板搭界处整个区域的应力都超过材料的屈服点，其PEEQ达到7.6%.提取变形最大点的载荷位移曲线见图8，可以明显看出结构在载荷4 000 N时，系统刚度趋于0，地板的变形急剧增大，发生屈曲失稳，导致计算无法收敛.由上文可知，Abaqus/Standard默认的非线性迭代方法和收敛准则很难越过该屈曲失稳点，并且载荷位移历程在失稳段的准确度也会降低.

对比水平压缩工况下位移云图和试验照片，可以看出仿真结果与试验结果高度一致，说明分析模型的精度可靠.其余工况下的分析结果汇总见表2.a）位移云图

b）应变云图

载荷/N残余

变形/mm最大

变形/mm塑性

应变/%向上压缩4 01241.57.6向上拉伸10.915.55.0向右压缩4 35226.35.0向右拉伸7.612.25.8向左压缩4 55648.28.4向左拉伸7.612.35.5水平压缩4 08042.27.6水平拉伸9.714.04.4向下压缩4 21642.37.7向下拉伸7.911.93.53.4优化方案

分析屈曲失稳发生的原因，主要是地板加强板在加载过程中发生塑性变形，导致系统刚度不断下降.在接近临界载荷时，塑性变形区域扩大到整个截面，致使结构突然塌陷.据此提出2种改进方案：（1）将地板加强板的厚度由0.7 mm提高至2 mm；（2）将地板加强板的材料由DC03提高到B340LA.

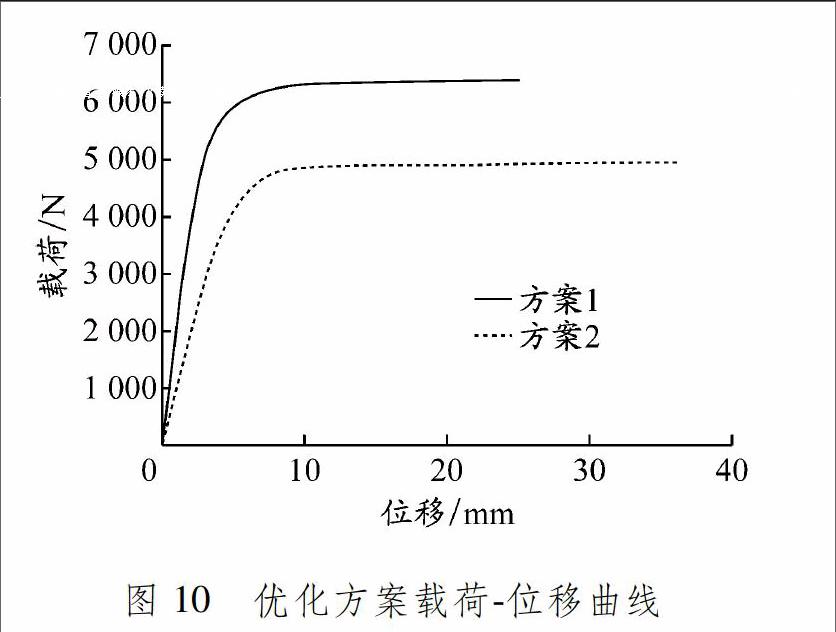
2种方案的目的都是提高系统的临界载荷，避免地板塌陷.考虑到原方案的向上压缩工况失稳载荷最小，因此在优化方案中只考虑该工况，以提高优化效率.2种优化方案的最大位移云图和等效塑性应变云图见图9.提取2种方案的失稳区域（方案一的拖钩安装板和方案二的地板加强梁）最大变形点的载荷位移曲线见图10.

a）方案1位移云图，mm

b）方案1应变云图

c）方案2位移云图，mm

d）方案2应变云图

根据方案1的分析结果可以看出：地板加强梁的刚度提升效果明显，未发生明显的凹陷；最大变形位置由地板转移到拖钩上，塌陷失稳的区域由地板加强梁转移到拖钩安装板上，主要原因是安装板的型面突变区域整体屈服，其最大等效塑性应变高达16.3%.根据载荷位移曲线可以看出：结构在6 200 N的时候无法继续加载，可见拖钩安装板的强度也不能满足设计要求，而且拖钩本体在弯折处也发生塑性变形，两者都需要进行加强.方案2的地板加强梁等效塑性应变为6.8%，屈曲失稳的临界载荷达到4 800 N，相对于原始方案性能有所提高，但是效果不如方案1明显.

综合考虑方案1和方案2的分析结果，可以判断整个牵引装置系统的强度性能都偏弱，从最差到最强顺序依次为地板加强梁、拖钩安装板、拖钩.在载荷增加过程中，三者依次发生塑性变形，随着塑性变形区域的扩大，进而发生屈曲失稳.为提高系统的抗压能力，设计出优化方案3：（1）将地板加强梁的厚度由0.7 mm提到1.8 mm，材料由DC03提高到B340LA；（2）拖钩安装板的厚度由1.2 mm提高到1.6 mm；（3）拖钩的材料由20#钢提高到45#钢.重新计算向上压缩工况，分析结果和载荷位移曲线见图11和12.将其余工况的分析结果列表汇总，见表3.a）位移云图

b）应变云图

图 11优化方案3的分析结果

Fig.11Analysis results of optimization scheme 3

Fig.12Loaddisplacement curves of optimization scheme 3表 3各工况下优化方案3分析结果

Tab.3Analysis results of optimization scheme 3 in

different cases工况残余

变形/mm最大

变形/mm塑性

应变/%向上压缩1.1 6.3 0.7 向上拉伸0.7 5.0 0.5 向右压缩0.7 5.6 1.7 向右拉伸0.5 4.5 1.5 向左压缩0.7 5.5 1.7 向左拉伸0.5 4.6 1.6 水平压缩1.0 5.9 0.6 水平拉伸0.5 4.5 0.4 向下压缩1.2 5.7 0.7 向下拉伸0.4 4.4 0.4

综上可知：新方案的最大变形和残余变形均低于目标值，无风险；塑性应变低于目标值，牵引装置强度性能满足设计要求，据此进行样件试制，装车后重新进行国标试验，顺利通过测试.

4结束语

本文阐述在最新的国标强制法规要求下利用非线性有限元方法对轻型汽车牵引装置进行强度分析，并提出优化方案，使其顺利通过国标强制试验.

从分析中可以看出，在牵引装置的强度性能开发中，压缩工况明显比拉伸工况更严苛，特别是受压载荷下，结构一旦发生断面规模的屈服现象，很容易产生屈曲失稳，引起整体失效.本文提出的分析方法和优化思路对于牵引装置的结构设计具有很强的指导意义.

参考文獻：

[1]明宇. 基于CAE技术的轿车拖钩分析与结构改进[J]. 汽车实用技术， 2016（1）： 151154. DOI： 10.16638/j.cnki.16717988.2016.01.051.

MING Y. Car front towing hook analysis and structural improvements based on CAE[J]. Automobile Applied Technology， 2016（1）： 151154. DOI： 10.16638/j.cnki.16717988.2016.01.051.

[2]轻型汽车牵引装置： GB 32087—2015[S].

[3]尚宝玲. 关于房车拖钩强度分析以及优化[J]. 轻型汽车技术， 2015（1/2）： 3034.

SHANG B L. Analysis and optimization on towing hook strength of a touring car[J]. Light Vehicles， 2015（1/2）： 3034.

[4]傅薇， 张影. 轿车拖钩强度分析[J]. 合肥工业大学学报（自然科学版）， 2009， 32（S1）： 101103.

FU W， ZHANG Y. Towing hook strength analysis for passenger car[J]. Journal of Hefei University of Technology（Natural Science）， 2009， 32（S1）： 101103.

[5]庄茁， 张帆， 岑松， 等. Abaqus非线性有限元分析与实例[M]. 北京： 科学出版社， 2005.

[6]石亦平， 周玉蓉. Abaqus有限元分析实例详解[M]. 北京： 机械工业出版社， 2006.

[7]王慎平， 刘北英. Abaqus中的非线性模拟[J]. 机械制造与自动化， 2006， 35（2）： 2022.

WANG S P， LIU B Y. Nonlinear analysis in Abaqus[J]. Machine Building & Automation， 2006， 35（2）： 2022.

[8]陈骥. 钢结构稳定理论与设计[M]. 北京： 科学出版社， 2001.第26卷 第1期2017年2月计 算 机 辅 助 工 程Computer Aided EngineeringVol.26 No.1Feb. 2017

[9]聂明皓， 瞿国钊， 张劲涛. 拱桥非线性稳定分析[J].交通科技， 2007（4）： 46.

NIE M H， QU G Z， ZHANG J T. Nonlinearity analysis of the stability of arch bridge[J]. Transportation Science & Technology， 2007（4）： 46.

[10]陈军明， 陈应波， 李秀才. 单层柱面网壳结构的非线性稳定性研究[J]. 武汉理工大学学报， 2003， 25（4）： 5154.

CHEN M J， CHEN Y B， LI X C. Study on nonlinear stability of singlelayer cylindrical reticulated shells[J]. Journal of Wuhan University of Technology， 2003， 25（4）： 5154.（編辑武晓英）第26卷 第1期2017年2月计 算 机 辅 助 工 程Computer Aided EngineeringVol.26 No.1Feb. 2017